1.4.2正弦函数、余弦函数的性质
文档属性
| 名称 | 1.4.2正弦函数、余弦函数的性质 |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-22 17:53:55 | ||
图片预览









文档简介
课件50张PPT。 正弦函数y=sinx,x∈[0, 2?]的图象中,
五个关键点是哪几个? 余弦函数y=cosx,x∈[0, 2?]的图象中,
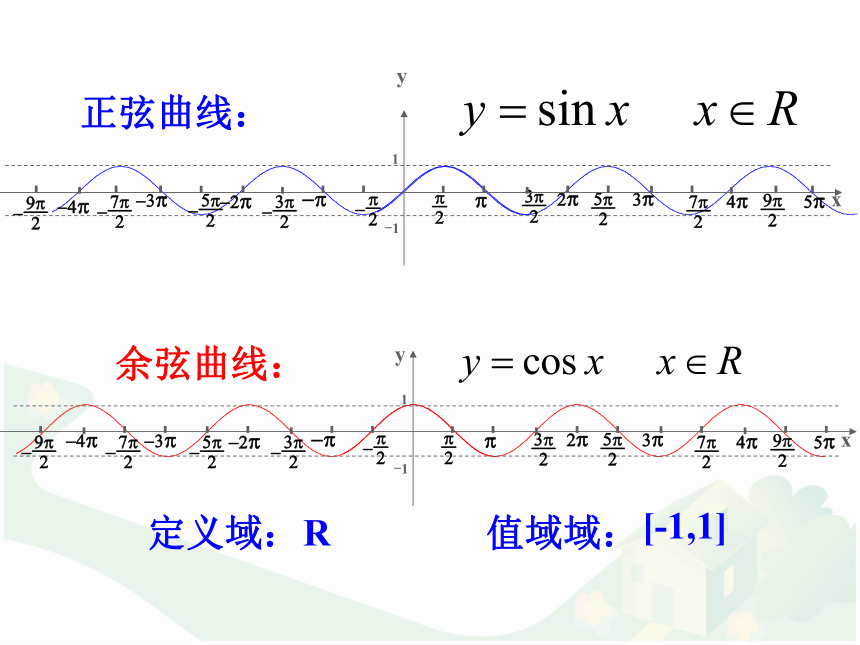
五个关键点是哪几个? 复习回顾定义域:值域域:R[-1,1] 1.4.2 正弦函数、余弦函数的性质每年都有春夏秋冬,它们周而复始的变化着.生活中,许多事物都有“周而复始”的变化规律.(1)今天是星期一,则过了七天是星期几?
过了十四天呢?……
(2)物理中的单摆振动、圆周运动,质点
运动的规律如何呢?这一些都给我们循环、重复的感觉,可以用
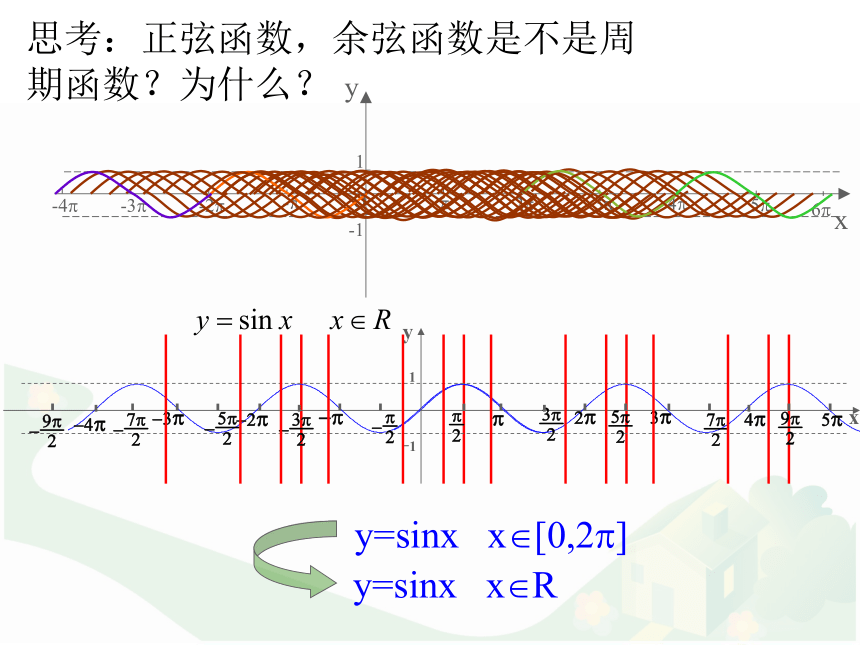
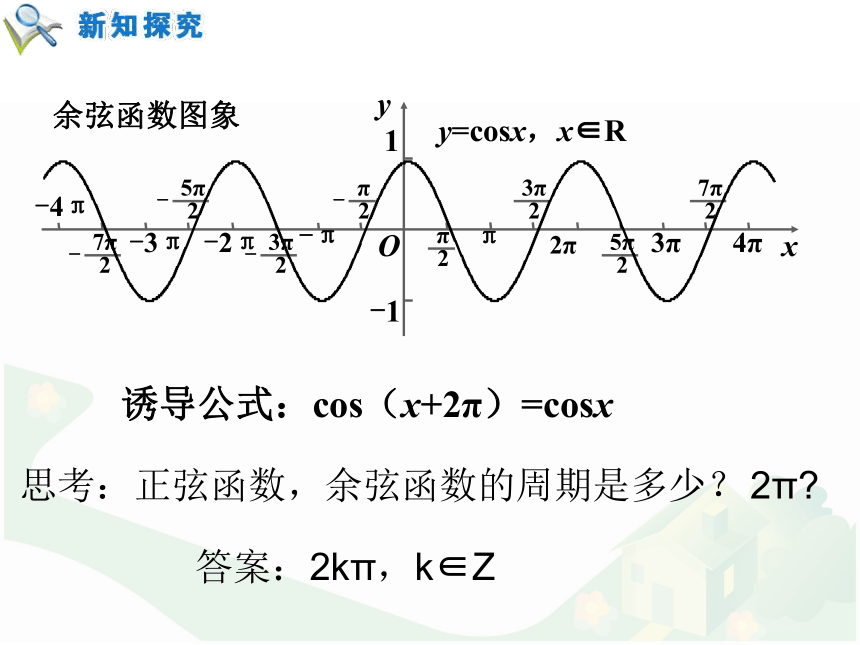
“周而复始”来描述,这就叫周期现象。 如果一个函数也存在周期现象,那它就是一个周期函数。 对于函数f(x)而言,如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有周期函数:那么函数f(x)就叫做周期函数.f(x+T)=f(x),非零常数T叫做这个函数的周期(period).思考:正弦函数,余弦函数是不是周期函数?为什么?正弦函数图象诱导公式:sin(x+2π)=sinx思考:正弦函数,余弦函数是不是周期函数?为什么?f(x+T)=f(x)?诱导公式:cos(x+2π)=cosx余弦函数图象思考:正弦函数,余弦函数的周期是多少?答案:2kπ,k∈Z2π? 如果在周期函数f(x)的所有周期中存在一个最小的正数,那么这个最小正数就叫做f(x)的最小正周期(minimal positive period). 特别地:今后所提及的周期,在没有特别说明的前提下,都是指函数的最小正周期.思考:正弦函数和余弦函数的最小正周期是多少?如果在周期函数f(x)的所有周期中存在一个最小的正数, 则这个最小正数叫做f(x)的最小正周期.
那么, 周期函数一定存在最小正周期吗?特别的y=c(c为常数)没有最小正周期。 正弦函数、余弦函数是周期函数,
2kπ(k∈Z, 且k≠0)都是它的周期,
且最小正周期是2π.就周期性而言,对正弦函数有什么结论?对余弦函数呢?例2:求下列函数的周期例2:求下列函数的周期练习:课本P36 2(1)(4)练习:课本P36 2(1)(4)2018/11/24【例1】 求函数的周期.全优23页典例剖析1.函数y=|sin x|的周期为________.π全优23页变式训练1.(2013年杭州模拟)函数的最小正周期为( )C全优24页基础夯实正弦、余弦函数的性质——奇偶性 请同学们观察正、余弦函数的图形,说出函数图象有怎样的对称性?其特点是什么?y=cosxy=sinxyyxx0011-1-1正弦函数是奇函数,余弦函数是偶函数.3.已知f(x)=ax+bsin x+1,若f(5)=7,则f(-5)=________.-5【解析】由f(5)=5a+bsin 5+1=7,得5a+bsin 5=6.∴f(-5)=-5a-bsin 5+1=-(5a+bsin 5)+1=-6+1=-5.全优87页限时规范训练 例3 求下列函数的最大值和最小值,并写出取最大值、最小值时自变量x的集合 (1)y=cosx+1,x∈R;(2)y=-3sin2x,x∈R. 例3 求下列函数的最大值和最小值,并写出取最大值、最小值时自变量x的集合 (1)y=cosx+1,x∈R;(2)y=-3sin2x,x∈R. 例3 求下列函数的最大值和最小值,并写出取最大值、最小值时自变量x的集合 (1)y=cosx+1,x∈R;(2)y=-3sin2x,x∈R.练习:课本P 40 3课本:练习40页 2课本:练习40页 4练习:课本 P40 1(1)(3)5.已知函数求:(1)该函数的定义域;故该函数的定义域为全优87页限时规范训练图象y=sinxy=cosxxoy-11xy-11性
质定义域RR值 域[-1,1][-1,1]周期性T=2T=2奇偶性奇函数偶函数单调性o三角函数的图象与性质【例2】 判断下列函数的奇偶性:(1)f(x)=lg(1-sin x)-lg(1+sin x);得-1<sin x<1,可见其定义域关于原点对称.又f(-x)=lg[1-sin(-x)]-lg[1+sin(-x)]=lg(1+sin x)-lg(1-sin x)=-f(x),所以f(x)=lg(1-sin x)-lg(1+sin x)为奇函数.全优23页典例剖析【例3】(2)求函数的值域.得到故函数的值域为[-5,1].全优23页典例剖析3.(2015年临沂测试)函数在区间上的最小值为( )B【解析】由已知故函数上的最小值为全优24页基础夯实 例4 比较下列各组数的大小: 例4 比较下列各组数的大小:练习:课本P 41 5(1)(2)练习:课本P 41 5(1)(2)例5 求函数 ,x∈[-2π,2π]的单调递增区间.例5 求函数 ,x∈[-2π,2π]的单调递增区间.练习P 41 6【例3】 (1)求函数的单调递减区间;【解析】(1)将化为可见,欲求的单调递减区间,只需求的单调递减区间.于是由解得故所求函数的单调递减区间为全优23页典例剖析思考:正弦曲线除了关于原点对称外,是否还关于其它的点和直线对称?(课本P46 11 ) 思考:余弦曲线除了关于y轴对称外,是否还关于其它的点和直线对称?
五个关键点是哪几个? 余弦函数y=cosx,x∈[0, 2?]的图象中,
五个关键点是哪几个? 复习回顾定义域:值域域:R[-1,1] 1.4.2 正弦函数、余弦函数的性质每年都有春夏秋冬,它们周而复始的变化着.生活中,许多事物都有“周而复始”的变化规律.(1)今天是星期一,则过了七天是星期几?
过了十四天呢?……
(2)物理中的单摆振动、圆周运动,质点
运动的规律如何呢?这一些都给我们循环、重复的感觉,可以用
“周而复始”来描述,这就叫周期现象。 如果一个函数也存在周期现象,那它就是一个周期函数。 对于函数f(x)而言,如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有周期函数:那么函数f(x)就叫做周期函数.f(x+T)=f(x),非零常数T叫做这个函数的周期(period).思考:正弦函数,余弦函数是不是周期函数?为什么?正弦函数图象诱导公式:sin(x+2π)=sinx思考:正弦函数,余弦函数是不是周期函数?为什么?f(x+T)=f(x)?诱导公式:cos(x+2π)=cosx余弦函数图象思考:正弦函数,余弦函数的周期是多少?答案:2kπ,k∈Z2π? 如果在周期函数f(x)的所有周期中存在一个最小的正数,那么这个最小正数就叫做f(x)的最小正周期(minimal positive period). 特别地:今后所提及的周期,在没有特别说明的前提下,都是指函数的最小正周期.思考:正弦函数和余弦函数的最小正周期是多少?如果在周期函数f(x)的所有周期中存在一个最小的正数, 则这个最小正数叫做f(x)的最小正周期.
那么, 周期函数一定存在最小正周期吗?特别的y=c(c为常数)没有最小正周期。 正弦函数、余弦函数是周期函数,
2kπ(k∈Z, 且k≠0)都是它的周期,
且最小正周期是2π.就周期性而言,对正弦函数有什么结论?对余弦函数呢?例2:求下列函数的周期例2:求下列函数的周期练习:课本P36 2(1)(4)练习:课本P36 2(1)(4)2018/11/24【例1】 求函数的周期.全优23页典例剖析1.函数y=|sin x|的周期为________.π全优23页变式训练1.(2013年杭州模拟)函数的最小正周期为( )C全优24页基础夯实正弦、余弦函数的性质——奇偶性 请同学们观察正、余弦函数的图形,说出函数图象有怎样的对称性?其特点是什么?y=cosxy=sinxyyxx0011-1-1正弦函数是奇函数,余弦函数是偶函数.3.已知f(x)=ax+bsin x+1,若f(5)=7,则f(-5)=________.-5【解析】由f(5)=5a+bsin 5+1=7,得5a+bsin 5=6.∴f(-5)=-5a-bsin 5+1=-(5a+bsin 5)+1=-6+1=-5.全优87页限时规范训练 例3 求下列函数的最大值和最小值,并写出取最大值、最小值时自变量x的集合 (1)y=cosx+1,x∈R;(2)y=-3sin2x,x∈R. 例3 求下列函数的最大值和最小值,并写出取最大值、最小值时自变量x的集合 (1)y=cosx+1,x∈R;(2)y=-3sin2x,x∈R. 例3 求下列函数的最大值和最小值,并写出取最大值、最小值时自变量x的集合 (1)y=cosx+1,x∈R;(2)y=-3sin2x,x∈R.练习:课本P 40 3课本:练习40页 2课本:练习40页 4练习:课本 P40 1(1)(3)5.已知函数求:(1)该函数的定义域;故该函数的定义域为全优87页限时规范训练图象y=sinxy=cosxxoy-11xy-11性
质定义域RR值 域[-1,1][-1,1]周期性T=2T=2奇偶性奇函数偶函数单调性o三角函数的图象与性质【例2】 判断下列函数的奇偶性:(1)f(x)=lg(1-sin x)-lg(1+sin x);得-1<sin x<1,可见其定义域关于原点对称.又f(-x)=lg[1-sin(-x)]-lg[1+sin(-x)]=lg(1+sin x)-lg(1-sin x)=-f(x),所以f(x)=lg(1-sin x)-lg(1+sin x)为奇函数.全优23页典例剖析【例3】(2)求函数的值域.得到故函数的值域为[-5,1].全优23页典例剖析3.(2015年临沂测试)函数在区间上的最小值为( )B【解析】由已知故函数上的最小值为全优24页基础夯实 例4 比较下列各组数的大小: 例4 比较下列各组数的大小:练习:课本P 41 5(1)(2)练习:课本P 41 5(1)(2)例5 求函数 ,x∈[-2π,2π]的单调递增区间.例5 求函数 ,x∈[-2π,2π]的单调递增区间.练习P 41 6【例3】 (1)求函数的单调递减区间;【解析】(1)将化为可见,欲求的单调递减区间,只需求的单调递减区间.于是由解得故所求函数的单调递减区间为全优23页典例剖析思考:正弦曲线除了关于原点对称外,是否还关于其它的点和直线对称?(课本P46 11 ) 思考:余弦曲线除了关于y轴对称外,是否还关于其它的点和直线对称?
