人教版湖南岳阳市华容县三中2023-2024学年度高二上学期数学模拟考试试卷(无答案)
文档属性
| 名称 | 人教版湖南岳阳市华容县三中2023-2024学年度高二上学期数学模拟考试试卷(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 505.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-30 08:46:58 | ||
图片预览


文档简介
湖南岳阳市华容县三中2023-2024学年度上学期
高二数学模拟考试试卷
考试说明:
(1)本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分.考试时间为120分钟;
(2)第I卷,第Ⅱ卷试题答案均答在答题卡上,交卷时只交答题卡
第I卷(选择题,共60分)
一、选择题(共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 已知圆的方程为,则圆心坐标为( )
A. B. C. D.
2. 若,且为第四象限角,则的值等于( )
A. B. C. D.
3. 四张卡片上分别写有数字,若从这四张卡片中随机抽取两张,则抽取的两张卡片上的数字之和为奇数的概率是( )
A. B. C. D.
4. 已知椭圆E:与双曲线C:()有相同的焦点,则双曲线C的渐近线方程为( )
A. B.
C. D.
5. 在区间上随机取一个数k,使直线与圆相交的概率为( )
A. B. C. D.
6. 已知均为锐角,,( )
A. B. C. D.
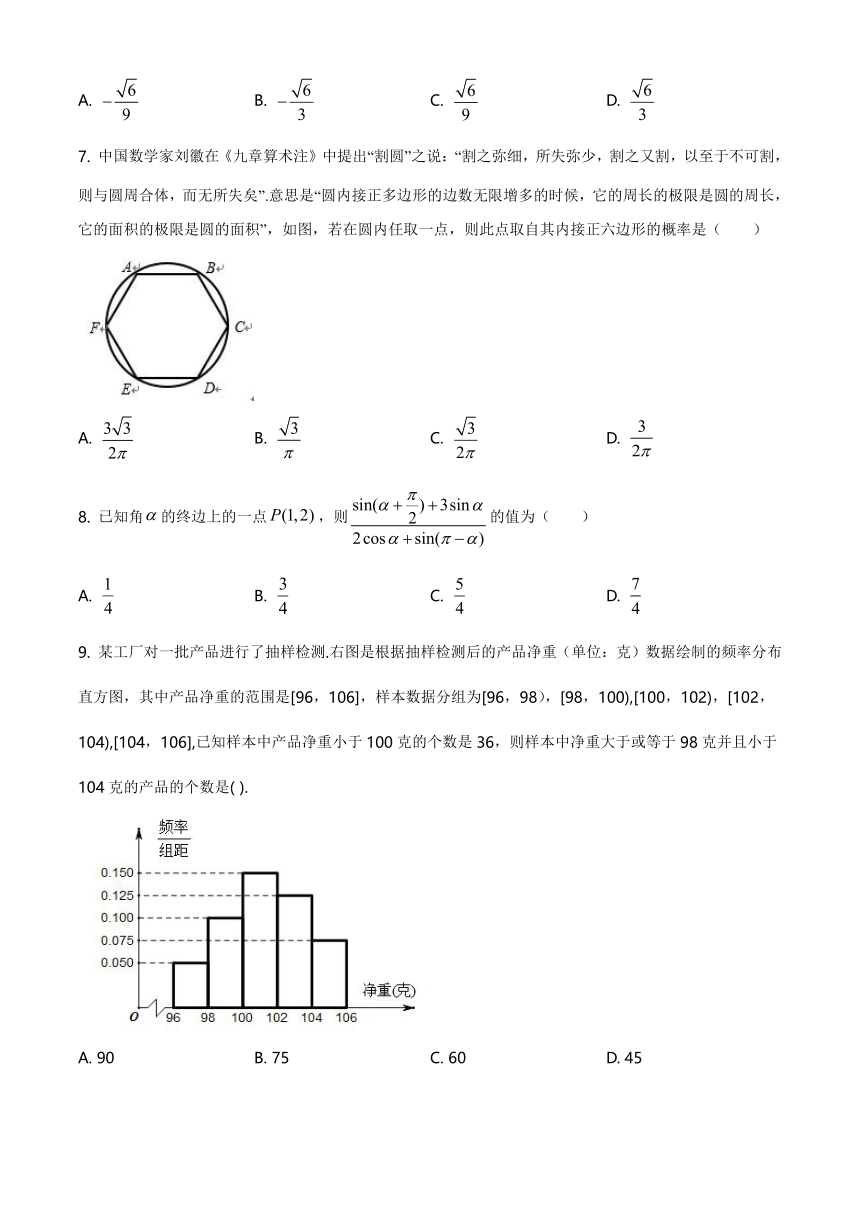
7. 中国数学家刘徽在《九章算术注》中提出“割圆”之说:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”.意思是“圆内接正多边形的边数无限增多的时候,它的周长的极限是圆的周长,它的面积的极限是圆的面积”,如图,若在圆内任取一点,则此点取自其内接正六边形的概率是( )
A. B. C. D.
8. 已知角的终边上的一点,则的值为( )
A. B. C. D.
9. 某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( ).
A. 90 B. 75 C. 60 D. 45
10. 在满足不等式组平面内随机取一点,设事件A=“”,那么事件A发生的概率是( )
A. B. C. D.
11. 6名同学参加4项社会实践活动,要求每项活动至少1人,则不同的参加方式共有( )
A. 2640种 B. 1560种 C. 1080种 D. 480种
12. 已知双曲线的左、右焦点分别为,为双曲线的右支上一点,且,与轴交于点,若是的平分线,则双曲线的离心率( )
A. B. C. D.
第Ⅱ卷(非选择题,共90分)
二、填空题(第13,14题每空4分,第15,16题每空3分,共20分,将答案填在答题卡相应的位置上,)
13. 某班共有56名学生,现将所有学生随机编号,用系统抽样的方法抽取一个容量为4的样本,已知12号、26号、54号同学在样本中,则样本中还有一名同学的编号是__________.
14. 已知正方体中,E为的中点,则异面直线AE与BC所成角的余弦值为 .
15. 下列说法中正确的个数是_________.
(1)命题“若,则方程有实数根”的逆否命题为“若方程无实数根,则”.
(2)命题“,”否定“,”.
(3)若为假命题,则,均为假命题.
(4)“”是“直线:与直线:平行”充要条件.
16. 已知双曲线E:的右顶点为A,抛物线C:的焦点为若在E的渐近线上存在点P,使得,则双曲线E的离心率的取值范围是______.
三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.)
17. 一个盒子里装有标号为的张标签,随机的选取两张标签.
(1)若标签的选取是无放回的,求两张标签上的数字为相邻整数的概率;
(2)若标签的选取是有放回的,求两张标签上的数字至少有一个为5的概率.
18. 某校共有学生2000人,其中男生1100人,女生900人为了调查该校学生每周平均课外阅读时间,采用分层抽样方法收集该校100名学生每周平均课外阅读时间(单位:小时)
(1)应抽查男生与女生各多少人?
(2)如图,根据收集100人的样本数据,得到学生每周平均课外阅读时间的频率分布直方图,其中样本数据分组区间为.若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
男生 女生 总计
每周平均课外阅读时间不超过2小时
每周平均课外阅读时间超过2小时
总计
附:
0.100 0.050 0.010 0.005
2.706 3.841 6.635 7879
19. 在平面直角坐标系中,已知点,动点到点的距离比到直线的距离小1个单位长度
(1)求动点的轨迹方程;
(2)若过点的直线与曲线交于两点,,求直线的方程.
20. 某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每本单价(元)试销l天,得到如表单价(元)与销量(册)数据:
单价(元)
销量(册)
(1)已知销量与单价具有线性相关关系,求关于的线性回归方程;
(2)若该书每本的成本为元,要使得售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
附:对于一组数据,,…,,其回归直线的斜率和截距的最小二乘估计分别为:,.
21. 近年来,来自“一带一路”沿线的20国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购.其中共享单车既响应绿色出行号召,节能减排,保护环境,又方便人们短距离出行,增强灵活性.某城市试投放3个品牌的共享单车分别为红车、黄车、蓝车,三种车的计费标准均为每15分钟(不足15分钟按15分钟计)1元,按每日累计时长结算费用,例如某人某日共使用了24分钟,系统计时为30分钟.A同学统计了他1个月(按30天计)每天使用共享单车的时长如茎叶图所示,不考虑每月自然因素和社会因素的影响,用频率近似代替概率.设A同学每天消费元.
(1)求的分布列及数学期望;
(2)各品牌为推广用户使用,推出APP注册会员的优惠活动:红车月功能使用费8元,每天消费打5折;黄车月功能使用费20元,每天前15分钟免费,之后消费打8折;蓝车月功能使用费45元,每月使用22小时之内免费,超出部分按每15分钟1元计费.设分别为红车,黄车,蓝车的月消费,写出与的函数关系式,参考(1)的结果,A同学下个月选择其中一个注册会员,他选哪个费用最低?
(3)该城市计划3个品牌共享单车共3000辆正式投入使用,为节约居民开支,随机调查了100名用户一周的平均使用时长如下表:
时长 (0,15] (15,30] (30,45] (45,60]
人数 16 45 34 5
在(2)的活动条件下,每个品牌各应该投放多少辆?
高二数学模拟考试试卷
考试说明:
(1)本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分.考试时间为120分钟;
(2)第I卷,第Ⅱ卷试题答案均答在答题卡上,交卷时只交答题卡
第I卷(选择题,共60分)
一、选择题(共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 已知圆的方程为,则圆心坐标为( )
A. B. C. D.
2. 若,且为第四象限角,则的值等于( )
A. B. C. D.
3. 四张卡片上分别写有数字,若从这四张卡片中随机抽取两张,则抽取的两张卡片上的数字之和为奇数的概率是( )
A. B. C. D.
4. 已知椭圆E:与双曲线C:()有相同的焦点,则双曲线C的渐近线方程为( )
A. B.
C. D.
5. 在区间上随机取一个数k,使直线与圆相交的概率为( )
A. B. C. D.
6. 已知均为锐角,,( )
A. B. C. D.
7. 中国数学家刘徽在《九章算术注》中提出“割圆”之说:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”.意思是“圆内接正多边形的边数无限增多的时候,它的周长的极限是圆的周长,它的面积的极限是圆的面积”,如图,若在圆内任取一点,则此点取自其内接正六边形的概率是( )
A. B. C. D.
8. 已知角的终边上的一点,则的值为( )
A. B. C. D.
9. 某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( ).
A. 90 B. 75 C. 60 D. 45
10. 在满足不等式组平面内随机取一点,设事件A=“”,那么事件A发生的概率是( )
A. B. C. D.
11. 6名同学参加4项社会实践活动,要求每项活动至少1人,则不同的参加方式共有( )
A. 2640种 B. 1560种 C. 1080种 D. 480种
12. 已知双曲线的左、右焦点分别为,为双曲线的右支上一点,且,与轴交于点,若是的平分线,则双曲线的离心率( )
A. B. C. D.
第Ⅱ卷(非选择题,共90分)
二、填空题(第13,14题每空4分,第15,16题每空3分,共20分,将答案填在答题卡相应的位置上,)
13. 某班共有56名学生,现将所有学生随机编号,用系统抽样的方法抽取一个容量为4的样本,已知12号、26号、54号同学在样本中,则样本中还有一名同学的编号是__________.
14. 已知正方体中,E为的中点,则异面直线AE与BC所成角的余弦值为 .
15. 下列说法中正确的个数是_________.
(1)命题“若,则方程有实数根”的逆否命题为“若方程无实数根,则”.
(2)命题“,”否定“,”.
(3)若为假命题,则,均为假命题.
(4)“”是“直线:与直线:平行”充要条件.
16. 已知双曲线E:的右顶点为A,抛物线C:的焦点为若在E的渐近线上存在点P,使得,则双曲线E的离心率的取值范围是______.
三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.)
17. 一个盒子里装有标号为的张标签,随机的选取两张标签.
(1)若标签的选取是无放回的,求两张标签上的数字为相邻整数的概率;
(2)若标签的选取是有放回的,求两张标签上的数字至少有一个为5的概率.
18. 某校共有学生2000人,其中男生1100人,女生900人为了调查该校学生每周平均课外阅读时间,采用分层抽样方法收集该校100名学生每周平均课外阅读时间(单位:小时)
(1)应抽查男生与女生各多少人?
(2)如图,根据收集100人的样本数据,得到学生每周平均课外阅读时间的频率分布直方图,其中样本数据分组区间为.若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
男生 女生 总计
每周平均课外阅读时间不超过2小时
每周平均课外阅读时间超过2小时
总计
附:
0.100 0.050 0.010 0.005
2.706 3.841 6.635 7879
19. 在平面直角坐标系中,已知点,动点到点的距离比到直线的距离小1个单位长度
(1)求动点的轨迹方程;
(2)若过点的直线与曲线交于两点,,求直线的方程.
20. 某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每本单价(元)试销l天,得到如表单价(元)与销量(册)数据:
单价(元)
销量(册)
(1)已知销量与单价具有线性相关关系,求关于的线性回归方程;
(2)若该书每本的成本为元,要使得售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
附:对于一组数据,,…,,其回归直线的斜率和截距的最小二乘估计分别为:,.
21. 近年来,来自“一带一路”沿线的20国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购.其中共享单车既响应绿色出行号召,节能减排,保护环境,又方便人们短距离出行,增强灵活性.某城市试投放3个品牌的共享单车分别为红车、黄车、蓝车,三种车的计费标准均为每15分钟(不足15分钟按15分钟计)1元,按每日累计时长结算费用,例如某人某日共使用了24分钟,系统计时为30分钟.A同学统计了他1个月(按30天计)每天使用共享单车的时长如茎叶图所示,不考虑每月自然因素和社会因素的影响,用频率近似代替概率.设A同学每天消费元.
(1)求的分布列及数学期望;
(2)各品牌为推广用户使用,推出APP注册会员的优惠活动:红车月功能使用费8元,每天消费打5折;黄车月功能使用费20元,每天前15分钟免费,之后消费打8折;蓝车月功能使用费45元,每月使用22小时之内免费,超出部分按每15分钟1元计费.设分别为红车,黄车,蓝车的月消费,写出与的函数关系式,参考(1)的结果,A同学下个月选择其中一个注册会员,他选哪个费用最低?
(3)该城市计划3个品牌共享单车共3000辆正式投入使用,为节约居民开支,随机调查了100名用户一周的平均使用时长如下表:
时长 (0,15] (15,30] (30,45] (45,60]
人数 16 45 34 5
在(2)的活动条件下,每个品牌各应该投放多少辆?
同课章节目录
