人教版五年级下学期数学 长方体和正方体表面积表格式教案
文档属性
| 名称 | 人教版五年级下学期数学 长方体和正方体表面积表格式教案 |  | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-29 21:11:47 | ||
图片预览

文档简介
《长方体和正方体的表面积》微课教学设计
授课教师姓名 学科 小学数学 教龄
微课名称 《长方体和正方体的表面积》 视频长度 录制时间
学情分析 本课所学习的主要内容为长方体和正方体的表面积计算,教学重难点在于学生对长方形、正方体表面积的构成和特点的认识。在学习本课之前,学生已经掌握长方形、正方形的特征以及长方形、正方形的面积计算。结合学生对于生活中长方体和正方体的观察,学生对长方体表面积的求解方法已经具备一定的认知。基于以上的学情分析,教师尽量以图片或动画的方式展示正方体和表面积的构成,更加生动直观,利于学生理解,使学生记忆更加深刻。在教学活动设计上,应从解决现实问题入手,以问题驱动的方式引导学生学习。
教学目标 1.通过观察、操作,掌握长方体和正方体表面积的含义。 2.探索并掌握长方体的表面积的计算方法,并能解决一些简单的计算问题。 3.会应用长方体、正方体的表面积公式解决生活中的问题。
教学重难点 1.掌握长方体和正方体表面积计算方法。 2.会使用求解长方体和正方体表面积计算方法,解决生活中的问题。
设计思路 本堂课采用模拟真实生活情境的方式引发学生思考,以问题引导式的课堂导入方法,激发学生的学习兴趣。以图示法设计教学活动,更加生动形象,利于学生观察与思考,逐渐在授课过程中推导出长方体表面积公式。通过引导学生观察正方体的特点,结合先前的学习内容,可以让学生回忆旧知,增强新旧知识的结合,进而推导出正方体的表面积公式。最后通过生活实例,让学生在问题解决中应用公式,加强学生对于公式的理解和记忆。
教学过程
内 容 时间
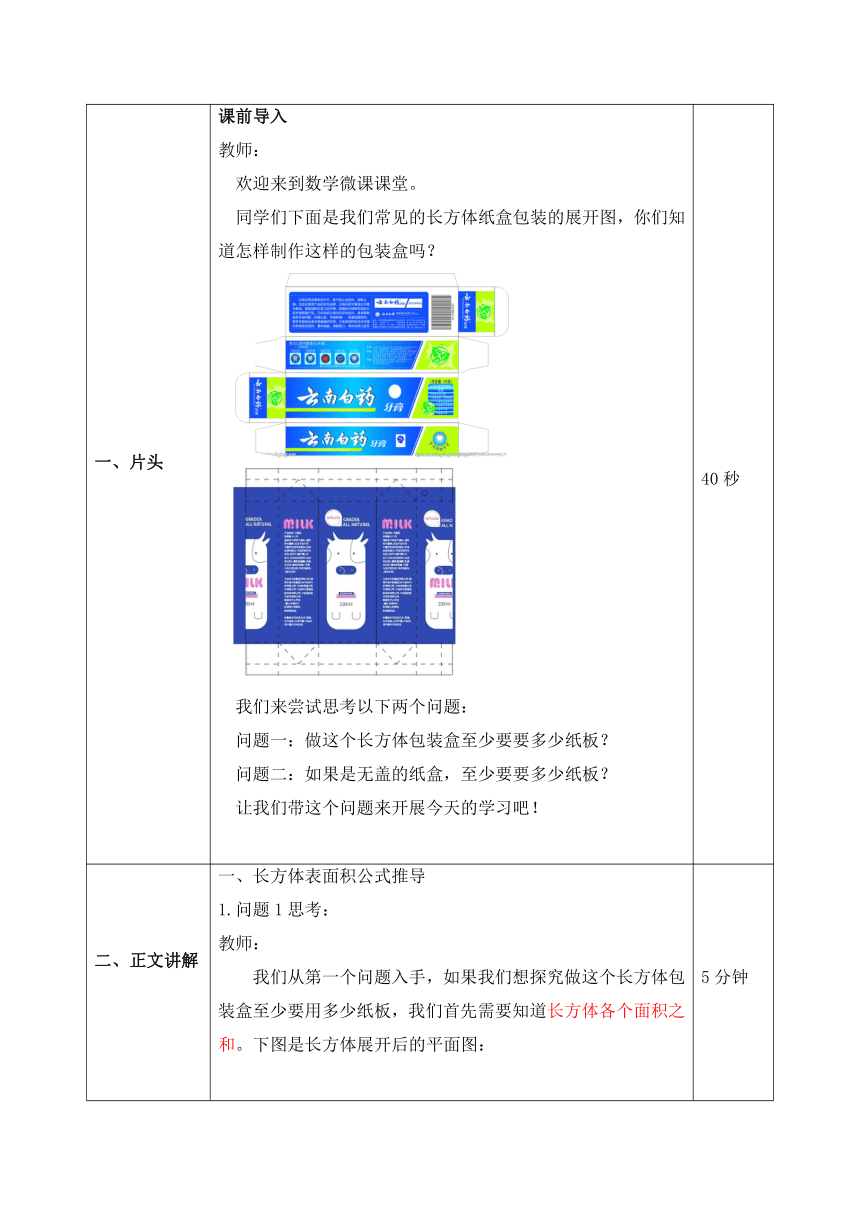
片头 课前导入 教师: 欢迎来到数学微课课堂。 同学们下面是我们常见的长方体纸盒包装的展开图,你们知道怎样制作这样的包装盒吗? 我们来尝试思考以下两个问题: 问题一:做这个长方体包装盒至少要要多少纸板? 问题二:如果是无盖的纸盒,至少要要多少纸板? 让我们带这个问题来开展今天的学习吧! 40秒
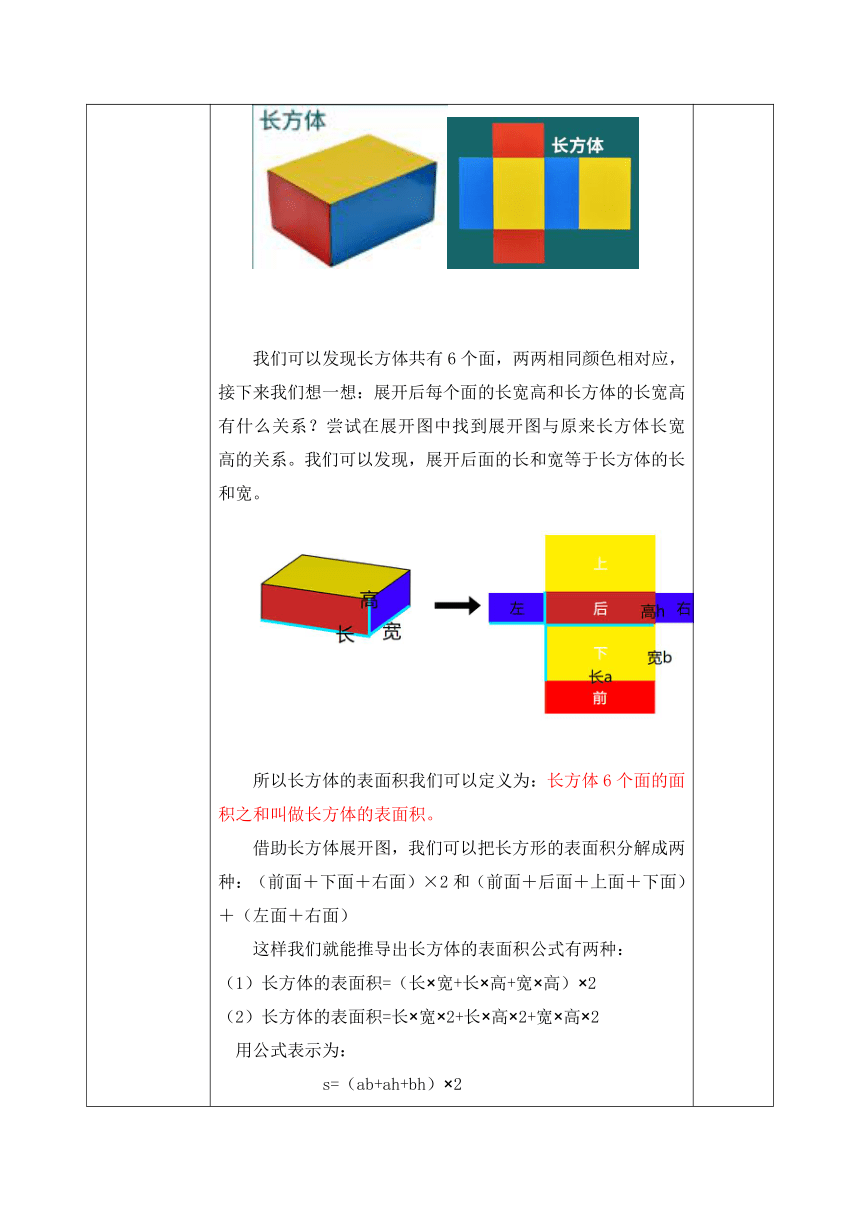
正文讲解 一、长方体表面积公式推导 1.问题1思考: 教师: 我们从第一个问题入手,如果我们想探究做这个长方体包装盒至少要用多少纸板,我们首先需要知道长方体各个面积之和。下图是长方体展开后的平面图: 我们可以发现长方体共有6个面,两两相同颜色相对应,接下来我们想一想:展开后每个面的长宽高和长方体的长宽高有什么关系?尝试在展开图中找到展开图与原来长方体长宽高的关系。我们可以发现,展开后面的长和宽等于长方体的长和宽。 所以长方体的表面积我们可以定义为:长方体6个面的面积之和叫做长方体的表面积。 借助长方体展开图,我们可以把长方形的表面积分解成两种:(前面+下面+右面)×2和(前面+后面+上面+下面)+(左面+右面) 这样我们就能推导出长方体的表面积公式有两种: 长方体的表面积=(长×宽+长×高+宽×高)×2 长方体的表面积=长×宽×2+长×高×2+宽×高×2 用公式表示为: s=(ab+ah+bh)×2 s=2ab+2ah+2bh 2.问题2思考: 我们回看第二个问题:如果是无盖的纸盒,至少要要多少纸板?无盖的纸盒是缺少了一个上面,于是长方体的表面积只需要去掉一个上表面的面积。 无盖长方体的表面积=长×宽+长×高×2+宽×高×2 s=ab+2ah+2bh 二、应用练习 练习一:日常的生活和生产中,我们需要计算长方体或正方体的表面积,下面我们想一想下面这个微波炉包装纸箱需要多少纸板? 教师: 我们在微波炉展开图中标注出了长宽高的数据(m), 将数字代入公式中我们可以得到长方体的表面积如下: (1)长方体的表面积=0.7×0.5×2+0.7×0.4×2+0.5×0.4×2 =1.66(m2) (2)长方体的表面积=(0.7x0.5+0.7x0.4+0.5x0.4)x2 =1.66(cm2) 三、正方体表面积公式推导 我们之前学习过正方形是特殊的长方形,正方体也是特殊的长方体吗?观察生活中常见的正方体,思考正方体的表面积如何求解。 我们可以发现正方体是长宽高都相等的正方体,也就是说正方体的6个面都相等,由长方体表面积公式我们可以推导出正方形表面积公式如下: 正方体的表面积=棱长×棱长×6 S=6a2 5分钟
三、巩固练习 教师: 如果你是礼品的的老板需要设计一款包装礼盒,你会怎么做呢?接下来让我们化身手工小能手,来设计一款抽屉式礼品盒吧! 1.礼品盒需要一个没有盖子的内盒,没有两侧的封套和一个最外层的纸袋,盒子的长宽高分别是20cm、15cm和7cm,定制这样的礼品套盒至少需要多少纸板呢? 首先是内盒,缺少了一个上面 前、后:20×7×2=280(cm2) 左、右:15×7×2=210(cm2) 下:15×20=300(cm2) 内盒总面积:280+210+300=790(cm2) 其次是封套,缺少了左右面 前、后:20×7×2=280(cm2) 上、下:15×20×2=600(cm2) 封套总面积:280+600=880(cm2) 最后是纸袋,缺少了一个侧面 前、后:20×7×2=280(cm2) 上、下:15×20×2=600(cm2) 侧面:15×7=105(cm2) 封套总面积:280+600+105=985(cm2) 礼品套盒总面积:790+880+985=2655(cm2) 答:至少需要2655cm2的纸板。 2分钟
结尾 本节课的重点在于长方体表面积公式的推导,在这个推导过程中我们将长方体进行展开,展开后认识到了长方体表面积是如何组成的,进而推导出长方形表面积的两个公式,通过两个公式都可以求解。然后通过观察、思考,我们发现正方体是棱长相等的特殊长方体,依据长方体表面积公式推导出正方体表面积公式。最后我们应用了公式解决了在生活会遇到的小问题,希望同学们在课后多加观察、多加练习,巩固知识。本次微课到此就结束了,谢谢观看! 20秒
授课教师姓名 学科 小学数学 教龄
微课名称 《长方体和正方体的表面积》 视频长度 录制时间
学情分析 本课所学习的主要内容为长方体和正方体的表面积计算,教学重难点在于学生对长方形、正方体表面积的构成和特点的认识。在学习本课之前,学生已经掌握长方形、正方形的特征以及长方形、正方形的面积计算。结合学生对于生活中长方体和正方体的观察,学生对长方体表面积的求解方法已经具备一定的认知。基于以上的学情分析,教师尽量以图片或动画的方式展示正方体和表面积的构成,更加生动直观,利于学生理解,使学生记忆更加深刻。在教学活动设计上,应从解决现实问题入手,以问题驱动的方式引导学生学习。
教学目标 1.通过观察、操作,掌握长方体和正方体表面积的含义。 2.探索并掌握长方体的表面积的计算方法,并能解决一些简单的计算问题。 3.会应用长方体、正方体的表面积公式解决生活中的问题。
教学重难点 1.掌握长方体和正方体表面积计算方法。 2.会使用求解长方体和正方体表面积计算方法,解决生活中的问题。
设计思路 本堂课采用模拟真实生活情境的方式引发学生思考,以问题引导式的课堂导入方法,激发学生的学习兴趣。以图示法设计教学活动,更加生动形象,利于学生观察与思考,逐渐在授课过程中推导出长方体表面积公式。通过引导学生观察正方体的特点,结合先前的学习内容,可以让学生回忆旧知,增强新旧知识的结合,进而推导出正方体的表面积公式。最后通过生活实例,让学生在问题解决中应用公式,加强学生对于公式的理解和记忆。
教学过程
内 容 时间
片头 课前导入 教师: 欢迎来到数学微课课堂。 同学们下面是我们常见的长方体纸盒包装的展开图,你们知道怎样制作这样的包装盒吗? 我们来尝试思考以下两个问题: 问题一:做这个长方体包装盒至少要要多少纸板? 问题二:如果是无盖的纸盒,至少要要多少纸板? 让我们带这个问题来开展今天的学习吧! 40秒
正文讲解 一、长方体表面积公式推导 1.问题1思考: 教师: 我们从第一个问题入手,如果我们想探究做这个长方体包装盒至少要用多少纸板,我们首先需要知道长方体各个面积之和。下图是长方体展开后的平面图: 我们可以发现长方体共有6个面,两两相同颜色相对应,接下来我们想一想:展开后每个面的长宽高和长方体的长宽高有什么关系?尝试在展开图中找到展开图与原来长方体长宽高的关系。我们可以发现,展开后面的长和宽等于长方体的长和宽。 所以长方体的表面积我们可以定义为:长方体6个面的面积之和叫做长方体的表面积。 借助长方体展开图,我们可以把长方形的表面积分解成两种:(前面+下面+右面)×2和(前面+后面+上面+下面)+(左面+右面) 这样我们就能推导出长方体的表面积公式有两种: 长方体的表面积=(长×宽+长×高+宽×高)×2 长方体的表面积=长×宽×2+长×高×2+宽×高×2 用公式表示为: s=(ab+ah+bh)×2 s=2ab+2ah+2bh 2.问题2思考: 我们回看第二个问题:如果是无盖的纸盒,至少要要多少纸板?无盖的纸盒是缺少了一个上面,于是长方体的表面积只需要去掉一个上表面的面积。 无盖长方体的表面积=长×宽+长×高×2+宽×高×2 s=ab+2ah+2bh 二、应用练习 练习一:日常的生活和生产中,我们需要计算长方体或正方体的表面积,下面我们想一想下面这个微波炉包装纸箱需要多少纸板? 教师: 我们在微波炉展开图中标注出了长宽高的数据(m), 将数字代入公式中我们可以得到长方体的表面积如下: (1)长方体的表面积=0.7×0.5×2+0.7×0.4×2+0.5×0.4×2 =1.66(m2) (2)长方体的表面积=(0.7x0.5+0.7x0.4+0.5x0.4)x2 =1.66(cm2) 三、正方体表面积公式推导 我们之前学习过正方形是特殊的长方形,正方体也是特殊的长方体吗?观察生活中常见的正方体,思考正方体的表面积如何求解。 我们可以发现正方体是长宽高都相等的正方体,也就是说正方体的6个面都相等,由长方体表面积公式我们可以推导出正方形表面积公式如下: 正方体的表面积=棱长×棱长×6 S=6a2 5分钟
三、巩固练习 教师: 如果你是礼品的的老板需要设计一款包装礼盒,你会怎么做呢?接下来让我们化身手工小能手,来设计一款抽屉式礼品盒吧! 1.礼品盒需要一个没有盖子的内盒,没有两侧的封套和一个最外层的纸袋,盒子的长宽高分别是20cm、15cm和7cm,定制这样的礼品套盒至少需要多少纸板呢? 首先是内盒,缺少了一个上面 前、后:20×7×2=280(cm2) 左、右:15×7×2=210(cm2) 下:15×20=300(cm2) 内盒总面积:280+210+300=790(cm2) 其次是封套,缺少了左右面 前、后:20×7×2=280(cm2) 上、下:15×20×2=600(cm2) 封套总面积:280+600=880(cm2) 最后是纸袋,缺少了一个侧面 前、后:20×7×2=280(cm2) 上、下:15×20×2=600(cm2) 侧面:15×7=105(cm2) 封套总面积:280+600+105=985(cm2) 礼品套盒总面积:790+880+985=2655(cm2) 答:至少需要2655cm2的纸板。 2分钟
结尾 本节课的重点在于长方体表面积公式的推导,在这个推导过程中我们将长方体进行展开,展开后认识到了长方体表面积是如何组成的,进而推导出长方形表面积的两个公式,通过两个公式都可以求解。然后通过观察、思考,我们发现正方体是棱长相等的特殊长方体,依据长方体表面积公式推导出正方体表面积公式。最后我们应用了公式解决了在生活会遇到的小问题,希望同学们在课后多加观察、多加练习,巩固知识。本次微课到此就结束了,谢谢观看! 20秒
