【新教材】第2章 两条直线平行和垂直的判定 人教A版(2019)高中数学选择性必修第一册课件(共47张PPT)
文档属性
| 名称 | 【新教材】第2章 两条直线平行和垂直的判定 人教A版(2019)高中数学选择性必修第一册课件(共47张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 00:00:00 | ||
图片预览









文档简介
(共47张PPT)
第二章直线和圆的方程
2.1 直线的倾斜角与斜率
2.1.2 两条直线平行和垂直的判定
学 习 目 标
核 心 素 养
1.理解并掌握两条直线平行的条件及两 条直线垂直的条件.
通过对两条直线平行
2.能根据已知条件判断两直线的平行与 垂直 .
与垂直的学习,提升直
观想象、逻辑推理和数
3.能应用两条直线的平行或垂直解决实 际问题.
学运算的数学素养.
.情景导学、探新 .知
有一天,著名魔术大师拿了一块长宽都是13分米的地毯去找地
毯匠,要求把这块正方形的地毯改制成宽8分米,长21分米的矩形,
地毯匠对魔术师说:这不可能吧,正方形的面积是169平方分米,而
矩形的面积只有168平方分米,除非裁去1平方分米.魔术师拿出事
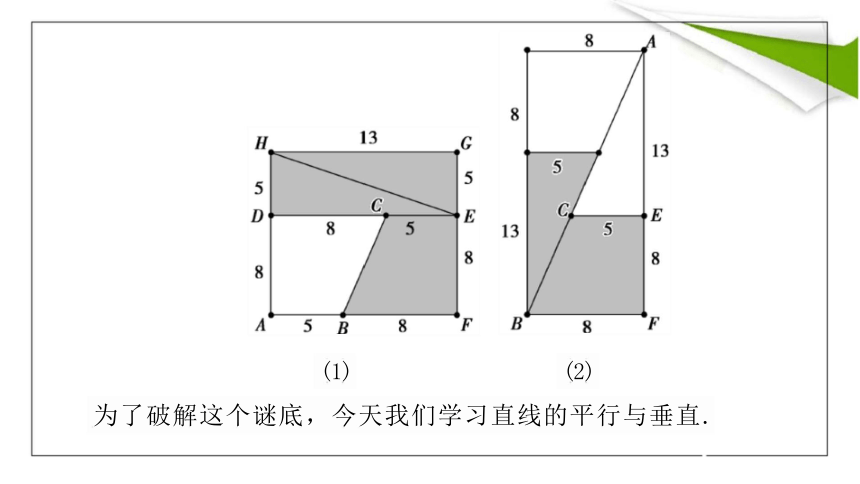
先准备好的两张图,对地毯匠说: “你就按图(1)的尺寸把地毯分成
情境引入·助学助教
魔术师的地毯
四块,然后按图(2)的样子拼在一起缝好就行了,我不会出错的,你
尽管放心做吧”.地毯匠照着做了,缝了一量,果真是宽8分米,长 21 分米.魔术师拿着改好的地毯得意洋洋地走了.而地毯匠还在纳 闷哩,这是什么回事呢
为了破解这个谜底,今天我们学习直线的平行与垂直.
(1) (2)
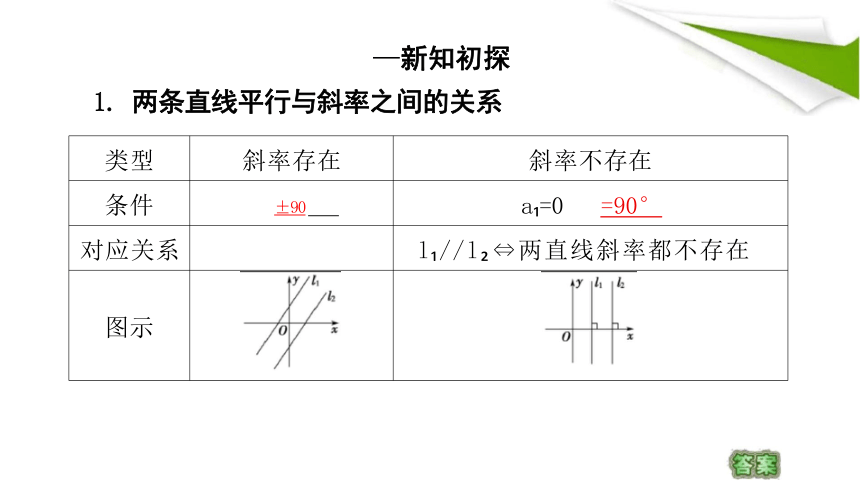
类型 斜率存在
斜率不存在
条件 ±90
a =0 =90°
对应关系
l //l 两直线斜率都不存在
图示
—新知初探
1. 两条直线平行与斜率之间的关系
[提示] 不一定.只有在两条直线的斜率都存在的情况下斜率才
相等.
思考:如果两条直线平行,那么这两条直线的斜率一定相等吗
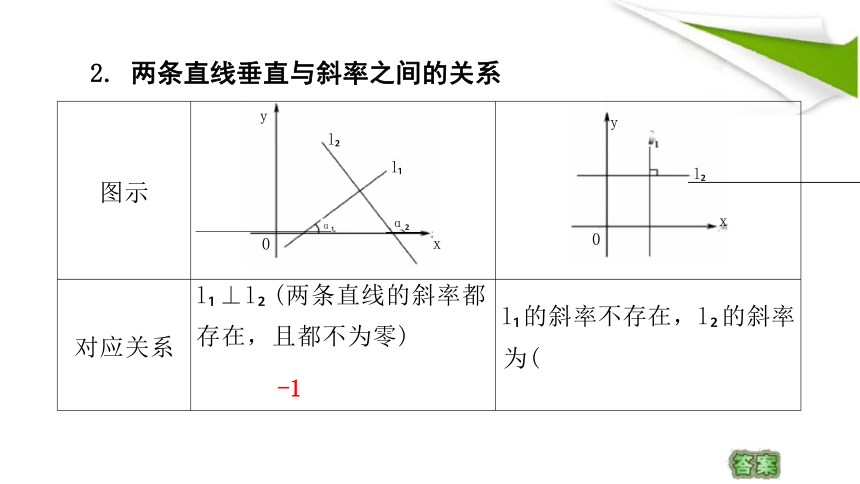
图示 y l l
y
l
x
0
α 0 α x
对应关系 l ⊥l (两条直线的斜率都 存在,且都不为零) -1
l 的斜率不存在,l 的斜率
为(
2. 两条直线垂直与斜率之间的关系
初试身手一
1. 思考辨析( 正确的打“ √ ”,错误的打“×”)
(1)平行的两条直线的斜率一定存在且相等.
(2)斜率相等的两条直线(两直线不重合)一定平行.
(3)只有斜率之积为一1的两条直线才垂直.
(4)若两条直线垂直,则斜率乘积为一1.
[提示] (1)×(2) √ (3)×(4)×
( )
( ) ( ) ( )
2.已 知A(2,0),B(3,3),直 线l//AB, 则直线l的斜率k 等 于 (
A.—3 B.3 C. D.
, ∵l//AB,∴k=3.]
辉析答案
B
3. 若直线l ,l 的方向向量分别为(1,—3)和(1,k), 且 l ⊥l ,
则k= .
[由于l ⊥l , 则(1,—3)·(1,k)=0,
即1 — 3k=0,∴
4 . (教材P T (1)改编)l 的斜率为
当 l ⊥l 时 ,m 的值为 .
,I 经过点A(1,1),B(0,m),
[由条件l ⊥l 得
解析答案
解得
合,作探、究、释、疑:难
类 型1 ] 两直线平行的判定及应用
【例1】 (1)根据下列给定的条件,判断直线l 与直线l 是否平行.
①l 经过点A(2,3),B (一4,0),l 经过点M(一3,1),N(一2,2);
②l 的斜率为 l 经过点A(4,2),B(2,3);
③l 平行于y 轴 ,l 经过点P(0, 一2),Q(0,5);
④l 经过点E(0,1),F (一2, — 1),l 经过点G(3,4),H(2,3).
(1)先求出两直线的斜率,再利用斜率进行判断;
(2)利用两直线平行的条件建立方程,解方程求得.
所以l 与 l 不平行.
②l 的斜率
与l 平行或重合.
[解](1)① 4
,kAB≠kMN,
所以 l
的斜率
③由题意,知l 的斜率不存在,且不与y 轴重合,l 的斜率也不
存在,且与y 轴重合,所以l //l .
④由题意,知 ,kEF=kGH, 所 以
l 与 l 平行或重合.
需进一步研究E,F,G,H 四点是否共线,
所以E,F,G,H 四点共线,所以l 与 l 重合.
(2)由题意知 CD 的斜率存在,则与其平行的直线AB 的斜率也存
在, 9
由于AB//CD, 所 以 即 解 得m=—2.
经验证m=—2 时,直线AB 的斜率存在,故m 的值为一2.
事
都不
存在
相等
否
不平行
规律方法 ● 0 费 费
判断两条不重合直线是否平行的步骤
看斜率
平行
平行
存在
是
1.已知口ABCD的三个顶点的坐标分别为A(0,1),B(1,0),C(4,3),
求顶点D的坐标.
[解] 设 D(m,n), 由题意,得AB//DC,AD//BC, 则 有kAB=
kpC,kAD=kBC.
所以 解 所以顶点D 的坐标为(3,4).
[跟进训练]
【例2】 (1)判断下列各题中l 与 l 是否垂直.
①l 经过点A(一1,一2),B(1,2);L 经过点M(一2,—1),N(2,1);
②l 的斜率为一10;l 经过点A(10,2),B(20,3);
③l 经过点A(3,4),B(3,10);l 经过点M(—10,40),N(10,40).
(2)已知直线l 经过点A(3,a),B(a—2,3), 直 线l 经过点C(2,3),
D(1,a—2), 如 果l ⊥l , 求a 的值.
类 型2 两直线垂直的判定及应用
(1)判断两直线垂直,当斜率存在时,利用k k = 一
1,若有一条斜率不存在时,判断另一条斜率是否为0.
(2)含字母的问题判断要分k 存在和不存在两种情况来解题.
②k =—10, k k =— 1, ∴l ⊥l .
③由A,B 的横坐标相等得
l 的倾斜角为90°,则l ⊥x轴 .
则 l //x 轴,∴l ⊥l .
[解](1
k k =1,∴l 与 l 不垂直.
(2)因为直线l 经过点C(2,3),D(1,a—2),所 以l 的斜率存在,
设为k .
当k =0, 即 a—2=3, 亦 即a=5 时 ,A(3,5),B(3,3), 显然直线
l 的斜率不存在,满足l ⊥l ; 当 k ≠0, 即 a—2≠3, 亦 即a≠5 时, 显然 l 的斜率存在,设为 k , 要满足题意,则 k k =—1, 得
解得a=2. 综上可知,a 的值为5或2 .
● 规律方法
利用斜率公式来判定两直线垂直的方法
(1)一看:就是看所给两点的横坐标是否相等,若相等,则直线
的斜率不存在只需看另一条直线的两点的纵坐标是否相等,若相等, 则垂直,若不相等,则进行第二步.
(2)二代:就是将点的坐标代入斜率公式.
(3)三求:计算斜率的值,进行判断.尤其是点的坐标中含有参
数时,应用斜率公式要对参数进行讨论.
2. 已知A(—m—3,2),B (一2m—4,4),C(—m,m),D(3,3m+2),
若直线AB⊥CD, 求 m 的值。
[跟进训练]
[解] ∵A,B 两点纵坐标不相等,
∴AB与 x 轴不平行 . ∵AB⊥CD,
∴CD 与 x 轴不垂直,∴—m≠3,m≠—3.
①当 AB 与 x 轴垂直时, —m—3=—2m—4, 解得m=—1. 当 m
= — 1 时C,D 两点的纵坐标均为一1.
∴CD//x 轴,此时AB⊥CD, 满足题意.
∵AB⊥CD,∴kAp·kcp=—1,
即 解得m=1.
综上,m 的值为1或—1.
②当AB 与 x 轴不垂直时,由斜率公式得
1. 两直线l //l k =k 成立的前提条件是什么
[提示] (1)两条直线的斜率存在;(2)两直线不重合.
类 型 3两直线平行与垂直的综合应用
[探究问题]
[提示] 不一定. 当两条直线的斜率都存在时,k k =—1, 还有
另一种情况就是, 一条直线斜率不存在,另一条直线斜率为零.
2.对任意两条直线,如果l ⊥l ,一 定有k k = —1 吗 为什么
【例3】 △ABC的顶点A(5,-1),B(1,1),C(2,m), 若 △ABC
是以点A 为直角顶点的直角三角形,求m 的值 .
[思路探究] 由 A 为直角顶点可得kAs·kAc=—1.
[解] 因为∠A为直角,则AC⊥AB,
所以kAc·kAB=—1,
得m=—7.
1.[变条件]本例中,将“C(2,m)” 改 为“C(2,3)”, 你能判断
三角形的形状吗
[解] 如 图 ,AB 边所在的直线的斜率 kAB
BC 边所在直线的斜率 kpc=2. 由 kAp·kpc
=—1,得AB⊥BC,即∠ABC=90° .
∴△ABC 是以点B 为直角顶点的直角三角形.
[母题探究]
2.[变条件]本例中若改为∠A 为锐角,其他条件不变,如何求解
m 的值
[解] 由于∠A 为锐角,故∠B 或 ∠C 为直角 .
若∠B 为直角,则AB⊥BC,
所以kAp·kBc=—1,
则 得 m=3.
若∠C为直角,则AC⊥BC,
所以kAc·kpc=—1,
得m=±2. 综上可知,m=3或m=±2.
3. [变条件]若将本例中的条件“点A 为直角顶点”去掉, 改 为
若△ABC 为直角三角形,如何求解m 的值
[解] 若∠A 为直角,
则 AC⊥AB,
所以kAc·kAB=—1,
即
得 m=—7;
若∠B 为直角,
则 AB⊥BC,
所以kAp·kBc=—1,
即
得m=3;
若∠C 为直角,则AC⊥BC,
所以kAckpc=—1,
即
得m=±2.
综上可知,m=—7 或 m=3 或 m=±2.
规律方法
利用两条直线平行或垂直判定图形形状的步骤
若斜率不存在,直接说明.若存在,根 据给定点的坐标求直线的斜率
结 论 由斜率之间的关系,判断形状
猜 测 根据描出的点,猜测图形的形状
描 点 在坐标系中描出给定的点
求斜率
课堂小结、提素养
斜率
直线
斜率均不存在
平行或重合
一条直线的斜率为0,另一条直线的斜率不存在
垂直
斜率均存在 相等
平行或重合
积为一1
垂直
必备素养
1. 两直线平行或垂直的判定方法
2.在两条直线平行或垂直关系的判断中体会分类讨论的思想.
学以致用一
1.下列说法正确的是( )
A. 若直线l 与 l 倾斜角相等,则l //l
B. 若直线l ⊥l , 则 k k =—1
C. 若直线的斜率不存在,则这条直线一定平行于y 轴
D. 若两条直线的斜率不相等,则两直线不平行
D [对 A, 两直线倾斜角相等,可能重合;对 B, 若 l ⊥l ,l
与l 中可能一条斜率不存在,另一条斜率为0;对C, 若直线斜率不 存在,可能与y 轴重合;对D, 若两条直线斜率不相等,则两条直线 一定不平行,综合可知D 正确 . ]
2.若直线l 的斜率为a,l ⊥l , 则直线l 的斜率为(
A. B.a
C. D. 或不存在
D [由l ⊥l , 当 a≠0 时, 当a=0 时 ,l 的斜率不存
在,故应选D.]
解析答案
3. 若经过点M(m,3) 和N(2,m) 的直线l 与斜率为一4的直线互相
垂直,则m 的值是 .
[由题意知,直线MN 的斜率存在,因为MN⊥l,
解得
4. 若两条直线 l ,l 的方向向量分别为(1,2)和(1,k), 当 l //l
时 ,k 的值为 _.
2 [l //l 时 k =k 或斜率均不存在,由条件可知k=2.]
直线l 的方向向量为(一2,1).
当l //l 时 得 m=3;
当l ⊥l 时, —2(一3—m)+3=0 得 故l //l 时 m=3,l ⊥l 时
5.直线I 经过点A(m,1),B(-3,4),直线l 经过点C(I,m),
D(—1,m+1), 当 l //l 或 l ⊥l 时,分别求实数m 的值 .
[解] 直线l 的方向向量为(一3—m,3),
第二章直线和圆的方程
2.1 直线的倾斜角与斜率
2.1.2 两条直线平行和垂直的判定
学 习 目 标
核 心 素 养
1.理解并掌握两条直线平行的条件及两 条直线垂直的条件.
通过对两条直线平行
2.能根据已知条件判断两直线的平行与 垂直 .
与垂直的学习,提升直
观想象、逻辑推理和数
3.能应用两条直线的平行或垂直解决实 际问题.
学运算的数学素养.
.情景导学、探新 .知
有一天,著名魔术大师拿了一块长宽都是13分米的地毯去找地
毯匠,要求把这块正方形的地毯改制成宽8分米,长21分米的矩形,
地毯匠对魔术师说:这不可能吧,正方形的面积是169平方分米,而
矩形的面积只有168平方分米,除非裁去1平方分米.魔术师拿出事
先准备好的两张图,对地毯匠说: “你就按图(1)的尺寸把地毯分成
情境引入·助学助教
魔术师的地毯
四块,然后按图(2)的样子拼在一起缝好就行了,我不会出错的,你
尽管放心做吧”.地毯匠照着做了,缝了一量,果真是宽8分米,长 21 分米.魔术师拿着改好的地毯得意洋洋地走了.而地毯匠还在纳 闷哩,这是什么回事呢
为了破解这个谜底,今天我们学习直线的平行与垂直.
(1) (2)
类型 斜率存在
斜率不存在
条件 ±90
a =0 =90°
对应关系
l //l 两直线斜率都不存在
图示
—新知初探
1. 两条直线平行与斜率之间的关系
[提示] 不一定.只有在两条直线的斜率都存在的情况下斜率才
相等.
思考:如果两条直线平行,那么这两条直线的斜率一定相等吗
图示 y l l
y
l
x
0
α 0 α x
对应关系 l ⊥l (两条直线的斜率都 存在,且都不为零) -1
l 的斜率不存在,l 的斜率
为(
2. 两条直线垂直与斜率之间的关系
初试身手一
1. 思考辨析( 正确的打“ √ ”,错误的打“×”)
(1)平行的两条直线的斜率一定存在且相等.
(2)斜率相等的两条直线(两直线不重合)一定平行.
(3)只有斜率之积为一1的两条直线才垂直.
(4)若两条直线垂直,则斜率乘积为一1.
[提示] (1)×(2) √ (3)×(4)×
( )
( ) ( ) ( )
2.已 知A(2,0),B(3,3),直 线l//AB, 则直线l的斜率k 等 于 (
A.—3 B.3 C. D.
, ∵l//AB,∴k=3.]
辉析答案
B
3. 若直线l ,l 的方向向量分别为(1,—3)和(1,k), 且 l ⊥l ,
则k= .
[由于l ⊥l , 则(1,—3)·(1,k)=0,
即1 — 3k=0,∴
4 . (教材P T (1)改编)l 的斜率为
当 l ⊥l 时 ,m 的值为 .
,I 经过点A(1,1),B(0,m),
[由条件l ⊥l 得
解析答案
解得
合,作探、究、释、疑:难
类 型1 ] 两直线平行的判定及应用
【例1】 (1)根据下列给定的条件,判断直线l 与直线l 是否平行.
①l 经过点A(2,3),B (一4,0),l 经过点M(一3,1),N(一2,2);
②l 的斜率为 l 经过点A(4,2),B(2,3);
③l 平行于y 轴 ,l 经过点P(0, 一2),Q(0,5);
④l 经过点E(0,1),F (一2, — 1),l 经过点G(3,4),H(2,3).
(1)先求出两直线的斜率,再利用斜率进行判断;
(2)利用两直线平行的条件建立方程,解方程求得.
所以l 与 l 不平行.
②l 的斜率
与l 平行或重合.
[解](1)① 4
,kAB≠kMN,
所以 l
的斜率
③由题意,知l 的斜率不存在,且不与y 轴重合,l 的斜率也不
存在,且与y 轴重合,所以l //l .
④由题意,知 ,kEF=kGH, 所 以
l 与 l 平行或重合.
需进一步研究E,F,G,H 四点是否共线,
所以E,F,G,H 四点共线,所以l 与 l 重合.
(2)由题意知 CD 的斜率存在,则与其平行的直线AB 的斜率也存
在, 9
由于AB//CD, 所 以 即 解 得m=—2.
经验证m=—2 时,直线AB 的斜率存在,故m 的值为一2.
事
都不
存在
相等
否
不平行
规律方法 ● 0 费 费
判断两条不重合直线是否平行的步骤
看斜率
平行
平行
存在
是
1.已知口ABCD的三个顶点的坐标分别为A(0,1),B(1,0),C(4,3),
求顶点D的坐标.
[解] 设 D(m,n), 由题意,得AB//DC,AD//BC, 则 有kAB=
kpC,kAD=kBC.
所以 解 所以顶点D 的坐标为(3,4).
[跟进训练]
【例2】 (1)判断下列各题中l 与 l 是否垂直.
①l 经过点A(一1,一2),B(1,2);L 经过点M(一2,—1),N(2,1);
②l 的斜率为一10;l 经过点A(10,2),B(20,3);
③l 经过点A(3,4),B(3,10);l 经过点M(—10,40),N(10,40).
(2)已知直线l 经过点A(3,a),B(a—2,3), 直 线l 经过点C(2,3),
D(1,a—2), 如 果l ⊥l , 求a 的值.
类 型2 两直线垂直的判定及应用
(1)判断两直线垂直,当斜率存在时,利用k k = 一
1,若有一条斜率不存在时,判断另一条斜率是否为0.
(2)含字母的问题判断要分k 存在和不存在两种情况来解题.
②k =—10, k k =— 1, ∴l ⊥l .
③由A,B 的横坐标相等得
l 的倾斜角为90°,则l ⊥x轴 .
则 l //x 轴,∴l ⊥l .
[解](1
k k =1,∴l 与 l 不垂直.
(2)因为直线l 经过点C(2,3),D(1,a—2),所 以l 的斜率存在,
设为k .
当k =0, 即 a—2=3, 亦 即a=5 时 ,A(3,5),B(3,3), 显然直线
l 的斜率不存在,满足l ⊥l ; 当 k ≠0, 即 a—2≠3, 亦 即a≠5 时, 显然 l 的斜率存在,设为 k , 要满足题意,则 k k =—1, 得
解得a=2. 综上可知,a 的值为5或2 .
● 规律方法
利用斜率公式来判定两直线垂直的方法
(1)一看:就是看所给两点的横坐标是否相等,若相等,则直线
的斜率不存在只需看另一条直线的两点的纵坐标是否相等,若相等, 则垂直,若不相等,则进行第二步.
(2)二代:就是将点的坐标代入斜率公式.
(3)三求:计算斜率的值,进行判断.尤其是点的坐标中含有参
数时,应用斜率公式要对参数进行讨论.
2. 已知A(—m—3,2),B (一2m—4,4),C(—m,m),D(3,3m+2),
若直线AB⊥CD, 求 m 的值。
[跟进训练]
[解] ∵A,B 两点纵坐标不相等,
∴AB与 x 轴不平行 . ∵AB⊥CD,
∴CD 与 x 轴不垂直,∴—m≠3,m≠—3.
①当 AB 与 x 轴垂直时, —m—3=—2m—4, 解得m=—1. 当 m
= — 1 时C,D 两点的纵坐标均为一1.
∴CD//x 轴,此时AB⊥CD, 满足题意.
∵AB⊥CD,∴kAp·kcp=—1,
即 解得m=1.
综上,m 的值为1或—1.
②当AB 与 x 轴不垂直时,由斜率公式得
1. 两直线l //l k =k 成立的前提条件是什么
[提示] (1)两条直线的斜率存在;(2)两直线不重合.
类 型 3两直线平行与垂直的综合应用
[探究问题]
[提示] 不一定. 当两条直线的斜率都存在时,k k =—1, 还有
另一种情况就是, 一条直线斜率不存在,另一条直线斜率为零.
2.对任意两条直线,如果l ⊥l ,一 定有k k = —1 吗 为什么
【例3】 △ABC的顶点A(5,-1),B(1,1),C(2,m), 若 △ABC
是以点A 为直角顶点的直角三角形,求m 的值 .
[思路探究] 由 A 为直角顶点可得kAs·kAc=—1.
[解] 因为∠A为直角,则AC⊥AB,
所以kAc·kAB=—1,
得m=—7.
1.[变条件]本例中,将“C(2,m)” 改 为“C(2,3)”, 你能判断
三角形的形状吗
[解] 如 图 ,AB 边所在的直线的斜率 kAB
BC 边所在直线的斜率 kpc=2. 由 kAp·kpc
=—1,得AB⊥BC,即∠ABC=90° .
∴△ABC 是以点B 为直角顶点的直角三角形.
[母题探究]
2.[变条件]本例中若改为∠A 为锐角,其他条件不变,如何求解
m 的值
[解] 由于∠A 为锐角,故∠B 或 ∠C 为直角 .
若∠B 为直角,则AB⊥BC,
所以kAp·kBc=—1,
则 得 m=3.
若∠C为直角,则AC⊥BC,
所以kAc·kpc=—1,
得m=±2. 综上可知,m=3或m=±2.
3. [变条件]若将本例中的条件“点A 为直角顶点”去掉, 改 为
若△ABC 为直角三角形,如何求解m 的值
[解] 若∠A 为直角,
则 AC⊥AB,
所以kAc·kAB=—1,
即
得 m=—7;
若∠B 为直角,
则 AB⊥BC,
所以kAp·kBc=—1,
即
得m=3;
若∠C 为直角,则AC⊥BC,
所以kAckpc=—1,
即
得m=±2.
综上可知,m=—7 或 m=3 或 m=±2.
规律方法
利用两条直线平行或垂直判定图形形状的步骤
若斜率不存在,直接说明.若存在,根 据给定点的坐标求直线的斜率
结 论 由斜率之间的关系,判断形状
猜 测 根据描出的点,猜测图形的形状
描 点 在坐标系中描出给定的点
求斜率
课堂小结、提素养
斜率
直线
斜率均不存在
平行或重合
一条直线的斜率为0,另一条直线的斜率不存在
垂直
斜率均存在 相等
平行或重合
积为一1
垂直
必备素养
1. 两直线平行或垂直的判定方法
2.在两条直线平行或垂直关系的判断中体会分类讨论的思想.
学以致用一
1.下列说法正确的是( )
A. 若直线l 与 l 倾斜角相等,则l //l
B. 若直线l ⊥l , 则 k k =—1
C. 若直线的斜率不存在,则这条直线一定平行于y 轴
D. 若两条直线的斜率不相等,则两直线不平行
D [对 A, 两直线倾斜角相等,可能重合;对 B, 若 l ⊥l ,l
与l 中可能一条斜率不存在,另一条斜率为0;对C, 若直线斜率不 存在,可能与y 轴重合;对D, 若两条直线斜率不相等,则两条直线 一定不平行,综合可知D 正确 . ]
2.若直线l 的斜率为a,l ⊥l , 则直线l 的斜率为(
A. B.a
C. D. 或不存在
D [由l ⊥l , 当 a≠0 时, 当a=0 时 ,l 的斜率不存
在,故应选D.]
解析答案
3. 若经过点M(m,3) 和N(2,m) 的直线l 与斜率为一4的直线互相
垂直,则m 的值是 .
[由题意知,直线MN 的斜率存在,因为MN⊥l,
解得
4. 若两条直线 l ,l 的方向向量分别为(1,2)和(1,k), 当 l //l
时 ,k 的值为 _.
2 [l //l 时 k =k 或斜率均不存在,由条件可知k=2.]
直线l 的方向向量为(一2,1).
当l //l 时 得 m=3;
当l ⊥l 时, —2(一3—m)+3=0 得 故l //l 时 m=3,l ⊥l 时
5.直线I 经过点A(m,1),B(-3,4),直线l 经过点C(I,m),
D(—1,m+1), 当 l //l 或 l ⊥l 时,分别求实数m 的值 .
[解] 直线l 的方向向量为(一3—m,3),
