【新教材】第2章 直线的一般式方程人教A版(2019)高中数学选择性必修第一册课件(共51张PPT)
文档属性
| 名称 | 【新教材】第2章 直线的一般式方程人教A版(2019)高中数学选择性必修第一册课件(共51张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-01 14:52:52 | ||
图片预览











文档简介
(共51张PPT)
第二章直线和圆的方程
2.2 直线的方程
2.2.3 直线的一般式方程
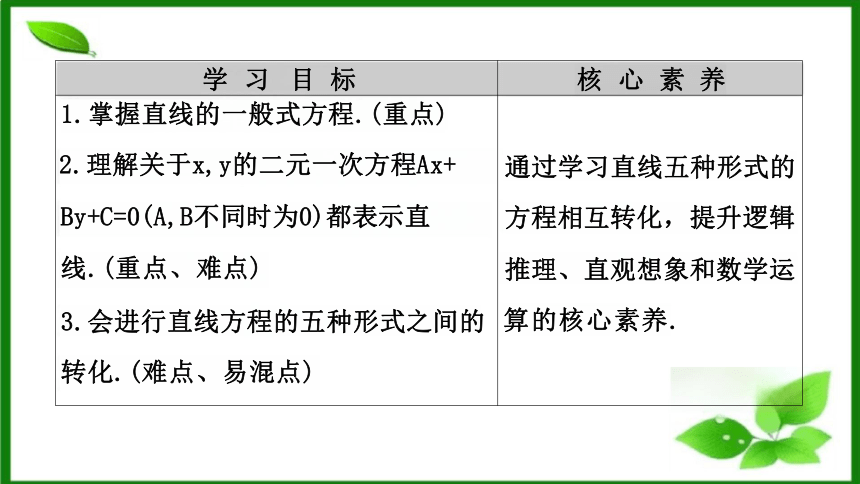
学 习 目 标
核 心 素 养
1.掌握直线的一般式方程.(重点)
2.理解关于x,y的二元一次方程Ax+ By+C=0(A,B不同时为0)都表示直 线.(重点、难点)
通过学习直线五种形式的
方程相互转化,提升逻辑
推理、直观想象和数学运
3.会进行直线方程的五种形式之间的 转化.(难点、易混点)
算的核心素养.
情境引入·助学助教
初中我们学习过二元一次方程,它的具体形式是Ax+By+C=0,
前面我们又学习了直线方程的点斜式: y—yo=k(x—xo), 斜截式: y
.它们都可以化成
为二元一次方程的这种形式,同时在一定条件下,这种形式也可以转 化为斜截式和截距式,我们把Ax+By+C=0(A、B 不同时为零)叫做 直线的一般式,下面进入今天的学习.
=kx+b, 两 点 和截距式:
新知初探一
直线的一般式方程
(1)定义:关于x,y 的二元一次方程Ax+ By+C =0 ( 其 中A,B
不同时为0)叫做直线的一般式方程,简称一般式.
(2)适用范围:平面直角坐标系中,任何一条直线都可用一般式
表示.
(3)系数的几何意义:
①当 B≠0 时,则 (斜率), 轴上的截距);
②当 B=0,A≠0 时,则 轴上的截距),此时不存在斜
率 .
思考:当 A=0 或 B=0 或 C=0 时,方程Ax+By+C=0 分别表
示什么样的直线
[提示] ( 1)若A=0, 则 表示与y 轴垂直的一条直线.
(2)若B=0, 则 表示与x 轴垂直的一条直线.
(3)若C=0, 则 Ax+By=0, 表示过原点的一条直线.
初 试 身 手
1. 思考辨析(正确的打“ √ ”,错误的打“×”)
(1)直线的一般式方程可以表示平面内任意一条直线. ( )
(2)直线的其他形式的方程都可化为一般式. ( )
(3)关于 x,y 的二元一次方程 Ax+By+C=0(A,B 不同时为0)
一定表示直线. ( )
[提示] (1) √ (2) √ (3) √
2.若方程Ax+By+C=0 表示直线,则A,B 应满足的条件为
( )
A. A≠0 B. B≠0
C. A·B≠0 D.A +B ≠0
D [方程 Ax+By+C=0 表示直线的条件为A,B 不能同时为0,
即A +B ≠0. 故选D.]
则a,b 的值分别为( )
A.—1,2 B.—2,2
C.2,—2 D.—2, —2
[y=0时,
解得a=— 1.]
3. 已知直线2x+ay+b=0 在x 轴、y 轴上的截距分别为一1,2,
解得b=2, 当 x=0 时,
A
60° [把3x—√3y+1=0 化成斜截式得
∴k=√3, 倾斜角为60°.]
4. 直线3x—√3y+1=0 的倾斜角为 .
5 . 直 的一般式方程是
得3x—2y-6=0.]
3x—2y—6=0 [ 1
【 例 1】 (1)已知直线l 的一般式方程为2x—3y+6=0, 请把 一
般式方程写成为斜截式和截距式方程,并指出斜率和它在坐标轴上的 截距.
直线的一般式方程与其他形式的互化
类型1
①斜率是 经过点A(8,一2);
②经过点B(4,2), 平行于x 轴;
③在x 轴和y 轴上的截距分别是 ,—3;
④经过两点P (3,一2),P (5,—4).
(2)根据下列各条件写出直线的方程,并且化成一般式.
[解] (1)由l 的一般式方程2x—3y+6=0 得斜截式方程为:
x+2.
截距式方程为:
由此可知,直线的斜率为 4 在x 轴 、y 轴上的截距分别为一3,2.
(2)①由点斜式得 事 即x+2y-4=0.
②由斜截式得y=2, 即y—2=0.
③由截距式 即 2x—y-3=0.
即x+y-1=0.
④由两点式得
规律方法
1. 求直线一般式方程的方法
已知点和斜率 选择点斜式
已知两点坐标 选择两点式 化为一般式方程 已知斜率和y轴截距 选择斜截式 Ax+By+C=0
已知两轴截距 选择截距式
2. 由直线方程的一般式转化为四种特殊形式时, 一定要注意其
运用的前提条件 .
1. 根据下列条件分别写出直线的方程,并化为一般式方程.
(1)斜率是 √3且经过点A(5,3);
(2)经过A(—1,5),B(2,—1) 两点;
(3)在x,y 轴上的截距分别是一3,—1.
[跟进训练]
[解](1)由点斜式方程可知,所求直线方程为y-3=√3(x-5),
化为一般式方程为 √3x-y+3-53=0.
(2)由两点式方程可知,所求直线方程 化为
一般式方程为2x+y—3=0.
(3)由截距式方程可得,所求直线方程 化为一般式
方程为x+3y+3=0.
类 型 2 直线的平行与垂直
【例2】 (1)已知直线l :2x+(m+1)y+4=0 与直线 l :mx+
3y—2=0 平行,求m 的值;
(2)当a 为何值时,直线l :(a+2)x+(1-a)y—1=0 与直线l :
(a—1)x+(2a+3)y+2=0 互相垂直.
利用两直线平行与垂直的条件,但要注意斜率的存
在与否.
时,显然l 与 l 不平行.
时,要使l //l ,
或m=—3,∴m 的值为2或—3.
[解] 法一:(1)由l :2x+(m+1)y+4=0,
l :mx+3y—2=0 知:
①当m=0
②当m≠0 解得m=2
(2)由题意知,直线l ⊥l .
①若 1 -a=0, 即 a=1 时,直线l :3x—1=0 与直线l :5y+2
=0显然垂直.
②若 2a+3=0,
5x—4=0 不垂直.
时,直线l :x +5y —2=0 与直线l :
即
. ∴a=—1.
综上可知,当a=1 或a=—1 时,直线l ⊥l .
③若1—a≠0且 2a+3≠0, 则直线l ,l 的斜率k ,k 都存在,
当l ⊥l 时 ,k ·k =—1,
9
法二: (1)令2×3=m(m+1),
解得m=—3 或 m=2.
当m=—3 时 ,l :x—y+2=0,l :3x—3y+2=0,
显然l 与 l 不重合,∴l //l .
同理当m=2 时 ,l :2x+3y+4=0,l :2x+3y—2=0,
显然l 与 l 不重合,∴l //l ,∴m 的值为2或一3.
(2)由题意知直线l ⊥l ,
∴(a+2)(a—1)+(1—a)(2a+3)=0, 解得a=±1,
将a=±1 代入方程,均满足题意.
故当a=1 或 a=—1 时,直线l ⊥l .
● 规律方法 ……
1. 直线l :A x+B y+C =0, 直 线l :A x+B y+C =0,
(1)若 l //l A B —A B =0 且 B C —B C ≠0 (或 A C 一
A C ≠0).
(2)若l ⊥l A A +B B =0.
2. 与直线Ax+By+C=0 平行的直线方程可设为Ax+By+m=
0(m≠C), 与直线Ax+By+C=0 垂直的直线方程可设为Bx—Ay+m
=0.
2.已知直线 l :x+my+6=0,
求m 的值,使得l 和 l :
(1)l //l ;(2)l ⊥l .
直 线 l :(m—2)x+3y+2m=0.
[跟进训练]
[解] (1)由1×3—m(m—2)=0 得 ,m=— 1 或 m=3.
当m=—1 时 ,l :x—y+6=0,l :3x—3y+2=0.
两直线显然不重合,即l //l .
当m=3 时 ,l :x+3y+6=0,l :x+3y+6=0.
两直线重合.故l //l 时 ,m 的值为一1.
故 l ⊥l 时 m 的值为
(2)由1×(m—2)+m×3=0 得
类 型 3 含参数的直线一般式方程问题
[探究问题]
1. 直 线kx—y+1—3k=0 是否过定点 若过定点,求出定点坐
标 .
[提示] kx—y+1-3k=0 可化为y-1=k(x—3), 由点斜式方程
可知该直线过定点(3,1).
2 .若直线y=kx+b(k≠0) 不经过第四象限,k,b 应满足什么条
件
[提示] 若直线 y=kx+b(k≠0) 不经过第四象限,则应满足 k>0
且b≥0.
【例3】 已知直线l:5ax—5y—a+3=0.
(1)求证:不论a 为何值,直线1总经过第一象限;
(2)为使直线1不经过第二象限,求a 的取值范围.
[思路探究] (1)当直线恒过第一象限内的一定点时,必然可得该
直线总经过第一象限;(2)直线不过第二象限即斜率大于0且与y 轴
的截距不大于0.
[解] (1)证明:法一:将直线l 的方程整理为
∴直线l 的斜率为 a, 且过定点 而点
限内,故不论a 为何值,l 恒过第一象限.
在第一象
法二:直 线l的方程可化为(5x—1)a—(5y—3)=0.
∵上式对任意的a 总成立,
以下同法一.
即 l 过定点
必
(2)直线OA 的斜率为
如图所示,要使l 不经过第二象限,
需斜率a≥koA=3,∴a≥3.
1. 本例中若直线在y 轴的截距为2,求字母 a 的值,这时直线
的一般式方程是什么
[解] 把 方 程 5ax-5y—a+3=0 化成斜截式方程为 y=ax+
由条件可知 解 得a=—7,
这时直线方程的一般式为:7x+y-2=0.
[母题探究]
2. 本例中,a 为何值时,已知直线与2x—y+3=0 平行 垂直
[解] 若两直线平行时,则
解得a=2,
若两直线垂直时,则5a×2+ (一5)×(一1)=0,
解得
故 a=2 时,两直线平行; 时两直线垂直.
3.本例中将方程改为“x—(a—1)y-a—2=0”, 若直线不经过
第二象限,则a 的取值范围又是什么
[解](1)当a—1=0, 即 a=1 时,直线为x=3, 该直线不经过
第二象限,满足要求.
(2)当a—1≠0, 即 a≠1 时,直线化为斜截式方程为
因为直线不过第二象限,故该直线的斜率大于等于零,且在y 轴的截距小于等于零, 解得 , 所 以
a>1.
综上可知a≥1.
规律方法
直线恒过定点的求解策略
(1)将方程化为点斜式,求得定点的坐标;
(2)将方程变形,把x,y 看作参数的系数,因为此式子对于任意的
参数的值都成立,故需系数为零,解方程组可得x,y 的值,即为直线 过的定点.
一般式 斜截式
截距式
Ax+By+C=0 B不同时为0) (B≠0)
B、
必备素养一
1. 直线方程的一般式与斜截式、截距式的互化
2.两个重要结论
结论1:平面直角坐标系中任何一条直线都可以用关于x 、y 的
二元一次方程Ax+By+C=0(A 、B 不同时为零)来表示.
结论2:任何关于x 、y 的二元一次方程Ax+By+C=0(A 、B 不
同时为零)都可以表示平面直角坐标系中的一条直线.
3. 根据两直线的一般式方程判定两直线平行和垂直的方法
一般地,设直线l :A x+B y+C =0,l :A x+B y+C =0.
(2)l ⊥l A A +B B =0.
条件( )
A.bc=0 B.a≠0
C.bc=0 且 a≠0 D.a≠0 且 b=c=0
D [y轴方程表示为x=0, 所 以a,b,c 满足条件为
b=c=0,a≠0.]
二学以 致 用一
表示的直线是y 轴,则系数a,b,c
1. 如 果ax+by+c=0
满足
2 . 直 线x—y-1=0 与坐标轴所围成的三角形的面积为( )
A. B.2 C.1 D.
D [由题意得直线与坐标轴交点为(1,0),(0,—1),故三角形面
积
2x-y+1=0 [由点斜式的 y-3=2(x—1), 整理得2x-y+1=
3.斜率为2,且经过点P(1,3)的直线的一般式方程为 .
0]
4 . 直线x—3y+4=0 与直线 mx+4y—1=0 互相垂直,则实数m
的值为
12 [因为两条直线垂直,∴1×m—3×4=0, 解 得m=12.]
5. 已知直线l 的方程为3x+4y—12=0, 求直线I 的一般式方程,
l'满足
(1)过点(一1,3),且与1平行;
(2)过点(一1,3),且与l 垂直.
[解] 法 一:(1)由题设1的方程可化为
∴l 的斜率为
由 I'与l平行,∴I'的斜率为
又∵I'过(一1,3),由点斜式知方程为 即 3x+4y
—9=0.
●
(2)由I'与l垂直,∴I 的斜率为 人
又∵I'过(一1,3),由点斜式可得方程为
即 4x—3y+13=0.
将点(一1,3)代入上式得m=—9.
∴所求直线方程为3x+4y—9=0.
(2)由l 与l 垂直,可设其方程为4x—3y+n=0.
将(—1,3)代入上式得n=13.
∴所求直线方程为4x—3y+13=0.
法二:(1)由l 与l 平行,可设I'方程为3x+4y +m=0.
第二章直线和圆的方程
2.2 直线的方程
2.2.3 直线的一般式方程
学 习 目 标
核 心 素 养
1.掌握直线的一般式方程.(重点)
2.理解关于x,y的二元一次方程Ax+ By+C=0(A,B不同时为0)都表示直 线.(重点、难点)
通过学习直线五种形式的
方程相互转化,提升逻辑
推理、直观想象和数学运
3.会进行直线方程的五种形式之间的 转化.(难点、易混点)
算的核心素养.
情境引入·助学助教
初中我们学习过二元一次方程,它的具体形式是Ax+By+C=0,
前面我们又学习了直线方程的点斜式: y—yo=k(x—xo), 斜截式: y
.它们都可以化成
为二元一次方程的这种形式,同时在一定条件下,这种形式也可以转 化为斜截式和截距式,我们把Ax+By+C=0(A、B 不同时为零)叫做 直线的一般式,下面进入今天的学习.
=kx+b, 两 点 和截距式:
新知初探一
直线的一般式方程
(1)定义:关于x,y 的二元一次方程Ax+ By+C =0 ( 其 中A,B
不同时为0)叫做直线的一般式方程,简称一般式.
(2)适用范围:平面直角坐标系中,任何一条直线都可用一般式
表示.
(3)系数的几何意义:
①当 B≠0 时,则 (斜率), 轴上的截距);
②当 B=0,A≠0 时,则 轴上的截距),此时不存在斜
率 .
思考:当 A=0 或 B=0 或 C=0 时,方程Ax+By+C=0 分别表
示什么样的直线
[提示] ( 1)若A=0, 则 表示与y 轴垂直的一条直线.
(2)若B=0, 则 表示与x 轴垂直的一条直线.
(3)若C=0, 则 Ax+By=0, 表示过原点的一条直线.
初 试 身 手
1. 思考辨析(正确的打“ √ ”,错误的打“×”)
(1)直线的一般式方程可以表示平面内任意一条直线. ( )
(2)直线的其他形式的方程都可化为一般式. ( )
(3)关于 x,y 的二元一次方程 Ax+By+C=0(A,B 不同时为0)
一定表示直线. ( )
[提示] (1) √ (2) √ (3) √
2.若方程Ax+By+C=0 表示直线,则A,B 应满足的条件为
( )
A. A≠0 B. B≠0
C. A·B≠0 D.A +B ≠0
D [方程 Ax+By+C=0 表示直线的条件为A,B 不能同时为0,
即A +B ≠0. 故选D.]
则a,b 的值分别为( )
A.—1,2 B.—2,2
C.2,—2 D.—2, —2
[y=0时,
解得a=— 1.]
3. 已知直线2x+ay+b=0 在x 轴、y 轴上的截距分别为一1,2,
解得b=2, 当 x=0 时,
A
60° [把3x—√3y+1=0 化成斜截式得
∴k=√3, 倾斜角为60°.]
4. 直线3x—√3y+1=0 的倾斜角为 .
5 . 直 的一般式方程是
得3x—2y-6=0.]
3x—2y—6=0 [ 1
【 例 1】 (1)已知直线l 的一般式方程为2x—3y+6=0, 请把 一
般式方程写成为斜截式和截距式方程,并指出斜率和它在坐标轴上的 截距.
直线的一般式方程与其他形式的互化
类型1
①斜率是 经过点A(8,一2);
②经过点B(4,2), 平行于x 轴;
③在x 轴和y 轴上的截距分别是 ,—3;
④经过两点P (3,一2),P (5,—4).
(2)根据下列各条件写出直线的方程,并且化成一般式.
[解] (1)由l 的一般式方程2x—3y+6=0 得斜截式方程为:
x+2.
截距式方程为:
由此可知,直线的斜率为 4 在x 轴 、y 轴上的截距分别为一3,2.
(2)①由点斜式得 事 即x+2y-4=0.
②由斜截式得y=2, 即y—2=0.
③由截距式 即 2x—y-3=0.
即x+y-1=0.
④由两点式得
规律方法
1. 求直线一般式方程的方法
已知点和斜率 选择点斜式
已知两点坐标 选择两点式 化为一般式方程 已知斜率和y轴截距 选择斜截式 Ax+By+C=0
已知两轴截距 选择截距式
2. 由直线方程的一般式转化为四种特殊形式时, 一定要注意其
运用的前提条件 .
1. 根据下列条件分别写出直线的方程,并化为一般式方程.
(1)斜率是 √3且经过点A(5,3);
(2)经过A(—1,5),B(2,—1) 两点;
(3)在x,y 轴上的截距分别是一3,—1.
[跟进训练]
[解](1)由点斜式方程可知,所求直线方程为y-3=√3(x-5),
化为一般式方程为 √3x-y+3-53=0.
(2)由两点式方程可知,所求直线方程 化为
一般式方程为2x+y—3=0.
(3)由截距式方程可得,所求直线方程 化为一般式
方程为x+3y+3=0.
类 型 2 直线的平行与垂直
【例2】 (1)已知直线l :2x+(m+1)y+4=0 与直线 l :mx+
3y—2=0 平行,求m 的值;
(2)当a 为何值时,直线l :(a+2)x+(1-a)y—1=0 与直线l :
(a—1)x+(2a+3)y+2=0 互相垂直.
利用两直线平行与垂直的条件,但要注意斜率的存
在与否.
时,显然l 与 l 不平行.
时,要使l //l ,
或m=—3,∴m 的值为2或—3.
[解] 法一:(1)由l :2x+(m+1)y+4=0,
l :mx+3y—2=0 知:
①当m=0
②当m≠0 解得m=2
(2)由题意知,直线l ⊥l .
①若 1 -a=0, 即 a=1 时,直线l :3x—1=0 与直线l :5y+2
=0显然垂直.
②若 2a+3=0,
5x—4=0 不垂直.
时,直线l :x +5y —2=0 与直线l :
即
. ∴a=—1.
综上可知,当a=1 或a=—1 时,直线l ⊥l .
③若1—a≠0且 2a+3≠0, 则直线l ,l 的斜率k ,k 都存在,
当l ⊥l 时 ,k ·k =—1,
9
法二: (1)令2×3=m(m+1),
解得m=—3 或 m=2.
当m=—3 时 ,l :x—y+2=0,l :3x—3y+2=0,
显然l 与 l 不重合,∴l //l .
同理当m=2 时 ,l :2x+3y+4=0,l :2x+3y—2=0,
显然l 与 l 不重合,∴l //l ,∴m 的值为2或一3.
(2)由题意知直线l ⊥l ,
∴(a+2)(a—1)+(1—a)(2a+3)=0, 解得a=±1,
将a=±1 代入方程,均满足题意.
故当a=1 或 a=—1 时,直线l ⊥l .
● 规律方法 ……
1. 直线l :A x+B y+C =0, 直 线l :A x+B y+C =0,
(1)若 l //l A B —A B =0 且 B C —B C ≠0 (或 A C 一
A C ≠0).
(2)若l ⊥l A A +B B =0.
2. 与直线Ax+By+C=0 平行的直线方程可设为Ax+By+m=
0(m≠C), 与直线Ax+By+C=0 垂直的直线方程可设为Bx—Ay+m
=0.
2.已知直线 l :x+my+6=0,
求m 的值,使得l 和 l :
(1)l //l ;(2)l ⊥l .
直 线 l :(m—2)x+3y+2m=0.
[跟进训练]
[解] (1)由1×3—m(m—2)=0 得 ,m=— 1 或 m=3.
当m=—1 时 ,l :x—y+6=0,l :3x—3y+2=0.
两直线显然不重合,即l //l .
当m=3 时 ,l :x+3y+6=0,l :x+3y+6=0.
两直线重合.故l //l 时 ,m 的值为一1.
故 l ⊥l 时 m 的值为
(2)由1×(m—2)+m×3=0 得
类 型 3 含参数的直线一般式方程问题
[探究问题]
1. 直 线kx—y+1—3k=0 是否过定点 若过定点,求出定点坐
标 .
[提示] kx—y+1-3k=0 可化为y-1=k(x—3), 由点斜式方程
可知该直线过定点(3,1).
2 .若直线y=kx+b(k≠0) 不经过第四象限,k,b 应满足什么条
件
[提示] 若直线 y=kx+b(k≠0) 不经过第四象限,则应满足 k>0
且b≥0.
【例3】 已知直线l:5ax—5y—a+3=0.
(1)求证:不论a 为何值,直线1总经过第一象限;
(2)为使直线1不经过第二象限,求a 的取值范围.
[思路探究] (1)当直线恒过第一象限内的一定点时,必然可得该
直线总经过第一象限;(2)直线不过第二象限即斜率大于0且与y 轴
的截距不大于0.
[解] (1)证明:法一:将直线l 的方程整理为
∴直线l 的斜率为 a, 且过定点 而点
限内,故不论a 为何值,l 恒过第一象限.
在第一象
法二:直 线l的方程可化为(5x—1)a—(5y—3)=0.
∵上式对任意的a 总成立,
以下同法一.
即 l 过定点
必
(2)直线OA 的斜率为
如图所示,要使l 不经过第二象限,
需斜率a≥koA=3,∴a≥3.
1. 本例中若直线在y 轴的截距为2,求字母 a 的值,这时直线
的一般式方程是什么
[解] 把 方 程 5ax-5y—a+3=0 化成斜截式方程为 y=ax+
由条件可知 解 得a=—7,
这时直线方程的一般式为:7x+y-2=0.
[母题探究]
2. 本例中,a 为何值时,已知直线与2x—y+3=0 平行 垂直
[解] 若两直线平行时,则
解得a=2,
若两直线垂直时,则5a×2+ (一5)×(一1)=0,
解得
故 a=2 时,两直线平行; 时两直线垂直.
3.本例中将方程改为“x—(a—1)y-a—2=0”, 若直线不经过
第二象限,则a 的取值范围又是什么
[解](1)当a—1=0, 即 a=1 时,直线为x=3, 该直线不经过
第二象限,满足要求.
(2)当a—1≠0, 即 a≠1 时,直线化为斜截式方程为
因为直线不过第二象限,故该直线的斜率大于等于零,且在y 轴的截距小于等于零, 解得 , 所 以
a>1.
综上可知a≥1.
规律方法
直线恒过定点的求解策略
(1)将方程化为点斜式,求得定点的坐标;
(2)将方程变形,把x,y 看作参数的系数,因为此式子对于任意的
参数的值都成立,故需系数为零,解方程组可得x,y 的值,即为直线 过的定点.
一般式 斜截式
截距式
Ax+By+C=0 B不同时为0) (B≠0)
B、
必备素养一
1. 直线方程的一般式与斜截式、截距式的互化
2.两个重要结论
结论1:平面直角坐标系中任何一条直线都可以用关于x 、y 的
二元一次方程Ax+By+C=0(A 、B 不同时为零)来表示.
结论2:任何关于x 、y 的二元一次方程Ax+By+C=0(A 、B 不
同时为零)都可以表示平面直角坐标系中的一条直线.
3. 根据两直线的一般式方程判定两直线平行和垂直的方法
一般地,设直线l :A x+B y+C =0,l :A x+B y+C =0.
(2)l ⊥l A A +B B =0.
条件( )
A.bc=0 B.a≠0
C.bc=0 且 a≠0 D.a≠0 且 b=c=0
D [y轴方程表示为x=0, 所 以a,b,c 满足条件为
b=c=0,a≠0.]
二学以 致 用一
表示的直线是y 轴,则系数a,b,c
1. 如 果ax+by+c=0
满足
2 . 直 线x—y-1=0 与坐标轴所围成的三角形的面积为( )
A. B.2 C.1 D.
D [由题意得直线与坐标轴交点为(1,0),(0,—1),故三角形面
积
2x-y+1=0 [由点斜式的 y-3=2(x—1), 整理得2x-y+1=
3.斜率为2,且经过点P(1,3)的直线的一般式方程为 .
0]
4 . 直线x—3y+4=0 与直线 mx+4y—1=0 互相垂直,则实数m
的值为
12 [因为两条直线垂直,∴1×m—3×4=0, 解 得m=12.]
5. 已知直线l 的方程为3x+4y—12=0, 求直线I 的一般式方程,
l'满足
(1)过点(一1,3),且与1平行;
(2)过点(一1,3),且与l 垂直.
[解] 法 一:(1)由题设1的方程可化为
∴l 的斜率为
由 I'与l平行,∴I'的斜率为
又∵I'过(一1,3),由点斜式知方程为 即 3x+4y
—9=0.
●
(2)由I'与l垂直,∴I 的斜率为 人
又∵I'过(一1,3),由点斜式可得方程为
即 4x—3y+13=0.
将点(一1,3)代入上式得m=—9.
∴所求直线方程为3x+4y—9=0.
(2)由l 与l 垂直,可设其方程为4x—3y+n=0.
将(—1,3)代入上式得n=13.
∴所求直线方程为4x—3y+13=0.
法二:(1)由l 与l 平行,可设I'方程为3x+4y +m=0.
