人教A版(2019)高中数学选择性必修第一册课件1.4.2 用空间向量研究距离、夹角问题 课件(共24张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册课件1.4.2 用空间向量研究距离、夹角问题 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-01 17:58:26 | ||
图片预览






文档简介
(共24张PPT)
第一章 空间向量与立体几何
1.4.2 用空间向量研究距离、夹角问题
新课引入
思考:怎样利用向量方法求直线到直线的距离、直线到平面的距
离、平面到平面的距离
提示:两条直线平行,其中一条直线到另一条直线间的距离是其中
一条直线上任一点到另一条直线的距离;
一条直线和一个平面平行,直线到平面的距离就是这条直线上任一
点到这个平面的距离;
两个平面平行,平面到平面的距离就是一个平面上任一点到这个平
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
面的距离.
新课引入
回顾求向量的投影公式是什么
回顾勾股定理是什么
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
已知直线l 的单位方向向量为u,A 是直线1上的定点,P 是直线l
外一点,设向量AP=a 在直线1上的投影向量为AQ=a-u, 则 点P 到直线
课堂探究
点P到直线的距离
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
l的距离为 (如图).
思考:u 怎么求
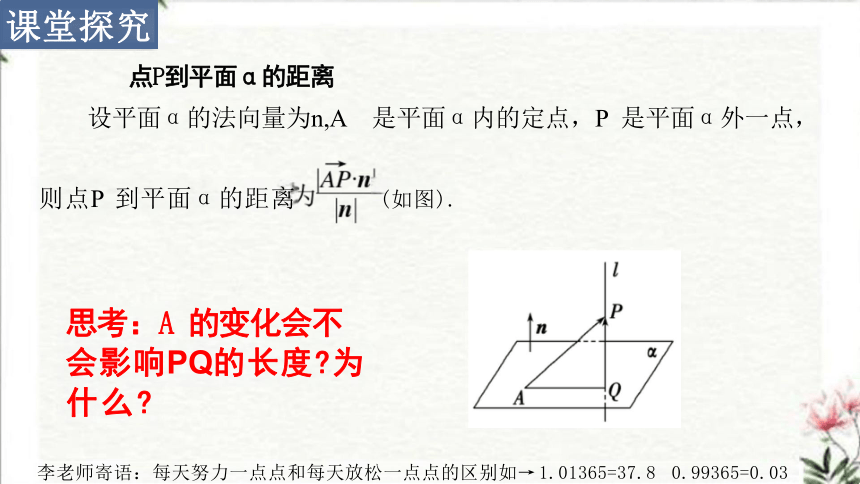
点P到平面α的距离
设平面α的法向量为n,A 是平面α内的定点,P 是平面α外一点,
思考:A 的变化会不
会影响PQ的长度 为 什么
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
则点P 到平面α的距离 (如图).
课堂探究
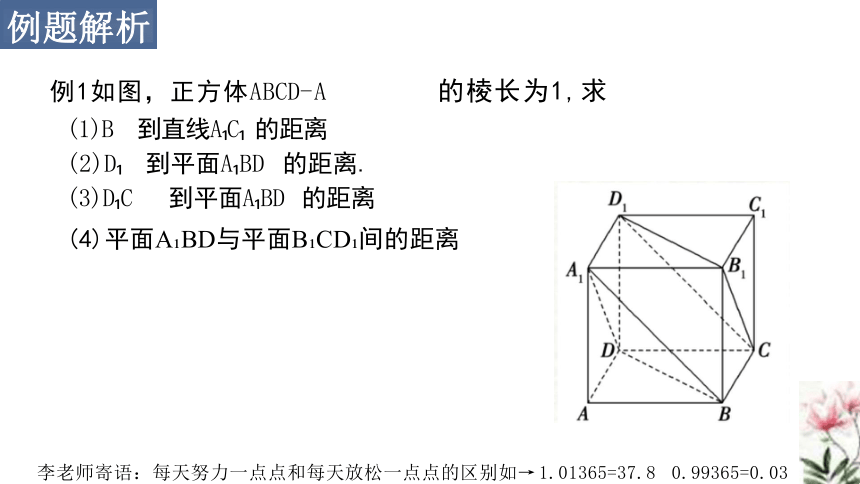
例1如图,正方体ABCD-A 的棱长为1,求
(1)B 到直线A C 的距离
(2)D 到平面A BD 的距离.
(3)D C 到平面A BD 的距离
(4)平面A BD与平面B CD 间的距离
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
例题解析
解 ( 1 )以B 为坐标原点,建立如图所示的空间直角坐标系,
则A (4,0,1),C (0,3,1),
所以直线A C 的方向向量
A C =(-4,3,0),BC =(0,3,1),
所以点B 到直线A C 的距离
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
例题解析
解 . (2)(3)(4)请学生回答,老 师书写,最后指出不足地方
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
例题解析
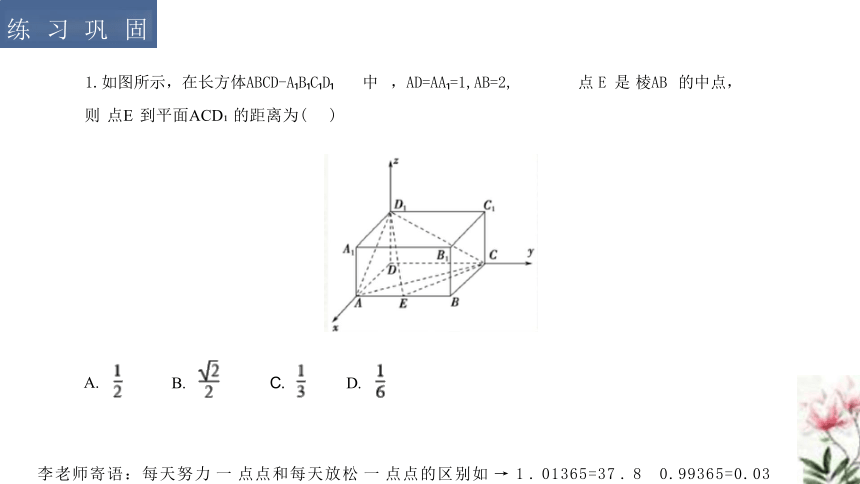
1.如图所示,在长方体ABCD-A B C D 中 ,AD=AA =1,AB=2, 点 E 是 棱AB 的中点,
则 点E 到平面ACD 的距离为( )
李老师寄语:每天努力 一 点点和每天放松 一 点点的区别如 → 1 . 01365=37 . 8 0.99365=0.03
练 习 巩 固
C.
A.
D.
B.
2.在空间直角坐标系中有长方体ABCD-A B C D ,A B=1,BC=2,AA =3, 则 点B 到直
线A C 的距离为( )
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
练习巩固
A. B.
C.
D.1
回顾夹角的定义和范围问题:
(1)线线
(2)向量的夹角
(3)线面
(4)二面角
(5)两个平面的夹角
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
重要
角的分类 向量求法
范围
两条异面直线 所成的角 设两异面直线l ,l 所成的角为θ,其方向向 量分别为u,v,则cos θ
直线与平面所 成的角 设直线AB与平面α所成的角为θ,直线AB 的方向向量为u,平面α的法向量为n,则 sin
两个平面的夹 角 设平面a与平面β的夹角为θ,平面a,β的 法向量分别为n ,n2,则cos
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.80.99365=0.03
空间角的向量法解法
点 ,EF与B D 相交于点H.
(1)求证:B D⊥平面ABD;
(2)求证:平面EGF//平面ABD;
(3)求平面EGF 与平面ABD 的距离
例3如图,在直三棱柱ABC-A B C
= 4 , 点E 在棱BB 上 ,EB =1,D,F,G
中,∠ABC=90°,BC=2,CC
分别为CC , C ,A C 的中
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
例题解析
[解析](1)证明:如图所示建立空间直角坐标系,
所以B D=(0,2,2),AB=(-a,0,0),BD=(0,2,一2).
所以B D·AB=0+0+0=0,B D·BD=0+4-4=0.
所以BD⊥AB,B D⊥BD,
所以B D⊥AB,B D⊥BD,
又AB∩BD=B, 所以B D⊥平面 ABD.
李 老 师 寄 语 : 每 天 努 力 一 点 点 和 每 天 放 松 一 点 点 的 区 别 如 → 1 . 0 1 3 6 5 = 3 7 . 8 0.99365=0.03
例 题 解 析
设 AB=a,
则A (a,0,0),B (0,0,0),C (0,2,0),F(0,1,0),E(0,0,1),A(a,0,4),
B(0,0,4),D(0,2,2),
例题解析
(2)证明:由(1)可得AB=(-a,0,0),BD=(0,2, 一2),
EF=(0,1, 一1),
所以AB=2GF,BD=2EF, 所以GF//AB,EF//BD.
所以GF//AB,EF//BD.
又GF∩EF=F,AB∩BD=B,
所以平面 EGF// 平面ABD.
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
(3)解:由(1)(2)知,B D是平面EGF 和平面ABD的法向量.
因为平面 EGF// 平 面ABD, 所 以 点E 到平面ABD 的距离就是两平
面的距离,设为d.
因为EB=(0,0,3),B D=(0,2,2),
即两平面间的距离
李 老 师 寄 语 : 每 天 努 力 一 点 点 和 每 天 放 松 一 点 点 的 区 别 如 → 1 . 0 1 3 6 5 = 3 7 . 8 0.99365=0.03
例 题 解 析
1.已知向量m,n 分别是直线l 与平面α的方向向量、法向量,若cos 〈m,n〉=
,则1与α所成的角为
B.60° C.150° D.120°
李 老 师 寄 语 : 每 天 努 力 一 点 点 和 每 天 放 松 一 点 点 的 区 别 如 → 1 . 0 1 3 6 5 = 3 7 . 8 0.99365=0.03
练 习 巩 固
解析 设l与α所成的角为θ,
∴θ=60°,
故选B.
2.已知平面α的法向量u=(1,0,-1), 平面的法向量v=(0,-1,1), 则平面a
与的夹角为
∴平面α与β的夹角
李 老 师 寄 语 : 每 天 努 力 一 点 点 和 每 天 放 松 一 点 点 的 区 别 如 → 1 . 0 1 3 6 5 = 3 7 . 8 0.99365=0.03
练 习 巩 固
3.如图,在三棱柱OAB-O A B 中,平面OBB O ⊥ 平面OAB, ∠O OB=60°,
∠AOB=90°,且OB=00 =2,OA=3, 求异面直线A B 与AO 所成角的余弦
李 老 师 寄 语 : 每 天 努 力 一 点 点 和 每 天 放 松 一 点 点 的 区 别 如 → 1 . 0 1 3 6 5 = 3 7 . 8 0.99365=0.03
练 习 巩 固
值.
解 以O 为坐标原点,OA,OB 的方向为x轴,y 轴的正方向.
建立如图所示的空间直角坐标系,
则O(0,0,0),O (0,1,√3),A(√3,0,0),A (√3,1,√3),B(0,2,0),
∴A B=(-√3,1, 一 √3),OA=(√3,-1, 一 √3).
∴异面直线A B 与 AO 所成角的余弦值为
李 老 师 寄 语 : 每 天 努 力 一 点 点 和 每 天 放 松 一 点 点 的 区 别 如 → 1 . 0 1 3 6 5 = 3 7 . 8 0.99365=0.03
练 习 巩 固
4.在空间直角坐标系Oxyz中,已知 A(1,-2,0),B(2,1, √6),则向量AB与平面 xOz的法向量的夹角的正弦值为
故向量AB与平面xOz的法向量的夹角的正弦值
李 老 师 寄 语 : 每 天 努 力 一 点 点 和 每 天 放 松 一 点 点 的 区 别 如 → 1 . 0 1 3 6 5 = 3 7 . 8 0.99365=0.03
解析 设平面xOz的法向量为n=(0,1,0),AB=(1,3, √6),
练 习 巩 固
5.如图,在正方体ABEF-DCE′F′ 中,M,N
(1)求直线MN 与直线AC 的夹角余弦值
(2)求直线EN与平面MNB 的夹角余弦值
(3)平面MNA与平面MNB 的夹角的余弦值
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
练习巩固
分别为AC,BF 的中点,求
课重小结
你学到了什么
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
作业1:报纸第2期2版
作业2:P33练习123
作业3:预习下一节
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
作业布置
第一章 空间向量与立体几何
1.4.2 用空间向量研究距离、夹角问题
新课引入
思考:怎样利用向量方法求直线到直线的距离、直线到平面的距
离、平面到平面的距离
提示:两条直线平行,其中一条直线到另一条直线间的距离是其中
一条直线上任一点到另一条直线的距离;
一条直线和一个平面平行,直线到平面的距离就是这条直线上任一
点到这个平面的距离;
两个平面平行,平面到平面的距离就是一个平面上任一点到这个平
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
面的距离.
新课引入
回顾求向量的投影公式是什么
回顾勾股定理是什么
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
已知直线l 的单位方向向量为u,A 是直线1上的定点,P 是直线l
外一点,设向量AP=a 在直线1上的投影向量为AQ=a-u, 则 点P 到直线
课堂探究
点P到直线的距离
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
l的距离为 (如图).
思考:u 怎么求
点P到平面α的距离
设平面α的法向量为n,A 是平面α内的定点,P 是平面α外一点,
思考:A 的变化会不
会影响PQ的长度 为 什么
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
则点P 到平面α的距离 (如图).
课堂探究
例1如图,正方体ABCD-A 的棱长为1,求
(1)B 到直线A C 的距离
(2)D 到平面A BD 的距离.
(3)D C 到平面A BD 的距离
(4)平面A BD与平面B CD 间的距离
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
例题解析
解 ( 1 )以B 为坐标原点,建立如图所示的空间直角坐标系,
则A (4,0,1),C (0,3,1),
所以直线A C 的方向向量
A C =(-4,3,0),BC =(0,3,1),
所以点B 到直线A C 的距离
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
例题解析
解 . (2)(3)(4)请学生回答,老 师书写,最后指出不足地方
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
例题解析
1.如图所示,在长方体ABCD-A B C D 中 ,AD=AA =1,AB=2, 点 E 是 棱AB 的中点,
则 点E 到平面ACD 的距离为( )
李老师寄语:每天努力 一 点点和每天放松 一 点点的区别如 → 1 . 01365=37 . 8 0.99365=0.03
练 习 巩 固
C.
A.
D.
B.
2.在空间直角坐标系中有长方体ABCD-A B C D ,A B=1,BC=2,AA =3, 则 点B 到直
线A C 的距离为( )
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
练习巩固
A. B.
C.
D.1
回顾夹角的定义和范围问题:
(1)线线
(2)向量的夹角
(3)线面
(4)二面角
(5)两个平面的夹角
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
重要
角的分类 向量求法
范围
两条异面直线 所成的角 设两异面直线l ,l 所成的角为θ,其方向向 量分别为u,v,则cos θ
直线与平面所 成的角 设直线AB与平面α所成的角为θ,直线AB 的方向向量为u,平面α的法向量为n,则 sin
两个平面的夹 角 设平面a与平面β的夹角为θ,平面a,β的 法向量分别为n ,n2,则cos
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.80.99365=0.03
空间角的向量法解法
点 ,EF与B D 相交于点H.
(1)求证:B D⊥平面ABD;
(2)求证:平面EGF//平面ABD;
(3)求平面EGF 与平面ABD 的距离
例3如图,在直三棱柱ABC-A B C
= 4 , 点E 在棱BB 上 ,EB =1,D,F,G
中,∠ABC=90°,BC=2,CC
分别为CC , C ,A C 的中
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
例题解析
[解析](1)证明:如图所示建立空间直角坐标系,
所以B D=(0,2,2),AB=(-a,0,0),BD=(0,2,一2).
所以B D·AB=0+0+0=0,B D·BD=0+4-4=0.
所以BD⊥AB,B D⊥BD,
所以B D⊥AB,B D⊥BD,
又AB∩BD=B, 所以B D⊥平面 ABD.
李 老 师 寄 语 : 每 天 努 力 一 点 点 和 每 天 放 松 一 点 点 的 区 别 如 → 1 . 0 1 3 6 5 = 3 7 . 8 0.99365=0.03
例 题 解 析
设 AB=a,
则A (a,0,0),B (0,0,0),C (0,2,0),F(0,1,0),E(0,0,1),A(a,0,4),
B(0,0,4),D(0,2,2),
例题解析
(2)证明:由(1)可得AB=(-a,0,0),BD=(0,2, 一2),
EF=(0,1, 一1),
所以AB=2GF,BD=2EF, 所以GF//AB,EF//BD.
所以GF//AB,EF//BD.
又GF∩EF=F,AB∩BD=B,
所以平面 EGF// 平面ABD.
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
(3)解:由(1)(2)知,B D是平面EGF 和平面ABD的法向量.
因为平面 EGF// 平 面ABD, 所 以 点E 到平面ABD 的距离就是两平
面的距离,设为d.
因为EB=(0,0,3),B D=(0,2,2),
即两平面间的距离
李 老 师 寄 语 : 每 天 努 力 一 点 点 和 每 天 放 松 一 点 点 的 区 别 如 → 1 . 0 1 3 6 5 = 3 7 . 8 0.99365=0.03
例 题 解 析
1.已知向量m,n 分别是直线l 与平面α的方向向量、法向量,若cos 〈m,n〉=
,则1与α所成的角为
B.60° C.150° D.120°
李 老 师 寄 语 : 每 天 努 力 一 点 点 和 每 天 放 松 一 点 点 的 区 别 如 → 1 . 0 1 3 6 5 = 3 7 . 8 0.99365=0.03
练 习 巩 固
解析 设l与α所成的角为θ,
∴θ=60°,
故选B.
2.已知平面α的法向量u=(1,0,-1), 平面的法向量v=(0,-1,1), 则平面a
与的夹角为
∴平面α与β的夹角
李 老 师 寄 语 : 每 天 努 力 一 点 点 和 每 天 放 松 一 点 点 的 区 别 如 → 1 . 0 1 3 6 5 = 3 7 . 8 0.99365=0.03
练 习 巩 固
3.如图,在三棱柱OAB-O A B 中,平面OBB O ⊥ 平面OAB, ∠O OB=60°,
∠AOB=90°,且OB=00 =2,OA=3, 求异面直线A B 与AO 所成角的余弦
李 老 师 寄 语 : 每 天 努 力 一 点 点 和 每 天 放 松 一 点 点 的 区 别 如 → 1 . 0 1 3 6 5 = 3 7 . 8 0.99365=0.03
练 习 巩 固
值.
解 以O 为坐标原点,OA,OB 的方向为x轴,y 轴的正方向.
建立如图所示的空间直角坐标系,
则O(0,0,0),O (0,1,√3),A(√3,0,0),A (√3,1,√3),B(0,2,0),
∴A B=(-√3,1, 一 √3),OA=(√3,-1, 一 √3).
∴异面直线A B 与 AO 所成角的余弦值为
李 老 师 寄 语 : 每 天 努 力 一 点 点 和 每 天 放 松 一 点 点 的 区 别 如 → 1 . 0 1 3 6 5 = 3 7 . 8 0.99365=0.03
练 习 巩 固
4.在空间直角坐标系Oxyz中,已知 A(1,-2,0),B(2,1, √6),则向量AB与平面 xOz的法向量的夹角的正弦值为
故向量AB与平面xOz的法向量的夹角的正弦值
李 老 师 寄 语 : 每 天 努 力 一 点 点 和 每 天 放 松 一 点 点 的 区 别 如 → 1 . 0 1 3 6 5 = 3 7 . 8 0.99365=0.03
解析 设平面xOz的法向量为n=(0,1,0),AB=(1,3, √6),
练 习 巩 固
5.如图,在正方体ABEF-DCE′F′ 中,M,N
(1)求直线MN 与直线AC 的夹角余弦值
(2)求直线EN与平面MNB 的夹角余弦值
(3)平面MNA与平面MNB 的夹角的余弦值
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
练习巩固
分别为AC,BF 的中点,求
课重小结
你学到了什么
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
作业1:报纸第2期2版
作业2:P33练习123
作业3:预习下一节
李老师寄语:每天努力一点点和每天放松一点点的区别如→ 1.01365=37.8 0.99365=0.03
作业布置
