2.3 二次函数与一元二次方程、不等式 说课课件(共37张PPT)2023-2024学年高一数学人教A版(2019)必修第一册
文档属性
| 名称 | 2.3 二次函数与一元二次方程、不等式 说课课件(共37张PPT)2023-2024学年高一数学人教A版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-01 00:00:00 | ||
图片预览









文档简介
(共37张PPT)
教材:
人教A版新课标高中数学必修一 第二章第三节第一课时
2.3二次函数与一元二次方程、不等式
说课
— —
说板书设计
说教学过程
说教法学法
说目标
03 04 05 06
目 录
说教材
说学情
02
01
在初中,我们从一次函数的角度看一元一次方程、 一元一 次不等式,发现了三者之间的内在联系,利用这种联系可以更 好地解决相关问题.对于二次函数、 一元二次方程和一元二次 不等式,是否也有这样的联系呢 先来看一个问题
问题 园艺师打算在绿地上用栅栏围一个矩形区域种
植花卉.若栅栏的长度是24 m, 围成的矩形区域的面积要
大于20 m , 则这个矩形的边长为多少米
设这个矩形的一条边长为x m, 则另 一条边长为
(12-x)m. 由题意,得
(12-x)x>20,
其中x ∈(x10x -12x+20<0,x∈{x10求得不等式①的解集,就得到了问题的答案.
一般地,我们把只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元
二次不等式 (quadric inequality in one unknown),一元二次不等式的一般形式是 ax +bx+c>0 或ax +bx+c<0,
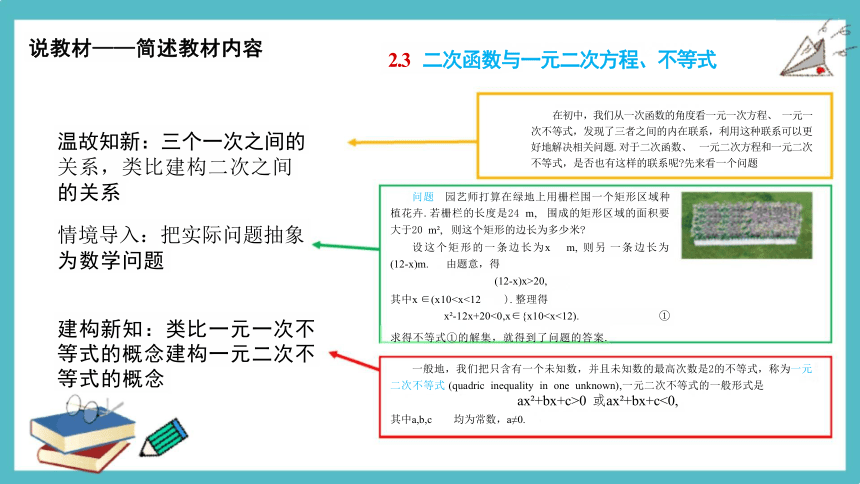
温故知新:三个一次之间的 关系,类比建构二次之间 的关系
情境导入:把实际问题抽象 为数学问题
建构新知:类比一元一次不 等式的概念建构一元二次不 等式的概念
2.3 二次函数与一元二次方程、不等式
说教材——简述教材内容
其中a,b,c 均为常数,a≠0.
y=ar +br+c 的零点.于是,二次函数y=x -12x+20 的两个零点是x =2,x =10.
从图2.3-1可以看出,二次函数y=x -12x+20 的两 个零点x =2.x =10 将x 轴分成三段.相应地,当x<2 或x>10 时,函数图象位于x 轴上方,此时y>0, 即 x -
12x+20>0; 当 2(x|2因为(x|2探究:通过二次函数图象与x轴的 交点进行思考,引入零点的定义, 零点将x轴分为不同的部分进而思 考对应y值的取值范围,也就是对 应不等式的解集
② 思考
在初中,我们学习了从一次函数的观点看一元一次方程、 一元一次不等式的思想
方法。类似地,能否从二次函数的观点看一元二次不等式,进而得到一元二次不等式 的求解方法呢
下面,我们先考察一元二次不等式x -12x+20<0 与二次函数y=x -12x+20 之 间的关系.
如图2.3-1,在平面直角坐标系中画出二次函数y=x -1 2x+20 的图象,图象与x 轴有两个交点,我们知道,这两个交点的横坐标就是方程x -12r+20=0 的两个实数根
x =2,x =10, 因此二次函数y=x -12 r+20 与x 轴的两个交点是(2,0)和(10,0).
一般地,对于二次函数y=ax +br+c, 我们把使ax +bx+c=0 的实数x 叫做二次函数
说教材——简述教材内容
启发:引导学生类比三个一 次之间的关系来思考一元二 次不等式解集的求解方法
y=x -12x+20
10
o 25 5 0x
-10
-1s
图2.3-1
△>0 △=0
△<0
y=ax +bx+c(a>0) 的图象 0x =
ax +br+c-0(a>0) 的根 有两个不相等的实数 根 x , r ( x < x ) 有两个相等的实数根 x=x=-
没有实数根
ax +bx+c>0(a>0) 的解集 (x |xx } (xlx≠-
R
ar +bx+c<0(a>0) 的解集 (x|x归纳:从特殊到一般,分类讨论二次函数 与一元二次方程、不等式的解的对应关系
得到x -5x+6>0 的解集。
例 2 求不等式9x -6x+1>0
例 3 求不等式-x +2x-3>0
说教材——简述教材内容
表2.3-1 二次函数与一元二次方程、不等式的解的对应关系
巩固:设计三道习题对一元二次 不等式的新知进行巩固练习
例 1 求不等式x -5x+6>0 分析:因为方程x -5x+6=0 的零点,所以先求出x -5r+6=0 的解集.
的根是函数y=x -5x+6
的根,再根据函数图象
的解集.
的解集.
二次函数与一元二次方程、不等式
② 思考
在初中。我们学习了从一次函数的观点看一元一次方程、 一无一次不等式的思想 方法。类假地,能否从二次温数的观点看一元二次不等式,进而得列一元二次不等式 的求解方进呢
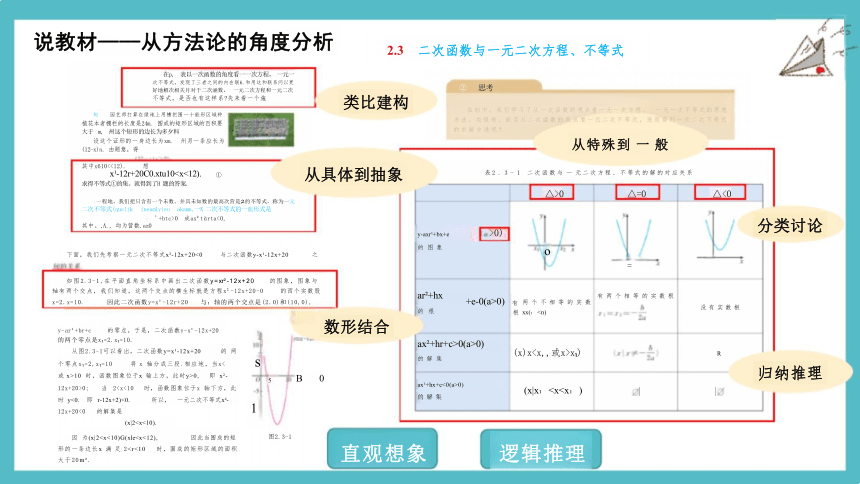
从特殊到 一 般
表2 . 3 - 1 二次函数与 一 元二次方程、不等式的解的对应关系
△>0 △=0 △<0
一般地,对于二次函数s=ar +hr+, 我们把陵a +hur+r=0 y-ar +br+c 的零点,于是,二次函数y-x -12x+20 的两个零点是x =2.x =10. 从图2.3-1可以看出,二次函数y=x -12x+20 的 两 个零点x =2,x =10 将 x 轴分成三段.相应地,当x< 或 x>10 时,函数图象位于x 输上方,此时y>0, 即 x - 12x+20>0; 当 2数形结合
0
s 5
1 -15
在p, 表以一次函数的角度看一一次方程, 一元一 次不等式,发现了三者之间的内在联6.和用这和联系问以更 好地解次相关月对于二次涵数, 一元二次方程和一元二次 不等式,是否也有这样系 先来看一个施
构 园艺师打算在绿地上用槽把围一十能形区域种
植花本者棚栏的长度是24m. 围或的矩形区域的百积要
大于 m, 州这个短形的边长为多夕料
设这个证形的一身边长为xm. 州另一条应长为
(12-x)n. 由题意,得
其中x610<<12). 想
x -12r+20C0.xtu10求得不等式①的集。就得到了H 题的答案.
一程地。我们把只含有一个未数。并具未知数的最高次营是2的不等式,称为一元 二次不等式(quslik ineumlyiso akamn,一K 二次不等式的一血形式是
ax '+btc>0 成ax tàrta<0,
其中。,A., 均为营数.az0
下面,我们先考察一元二次不等式x -12x+20<0 与二次函数y-x -12x+20 之
如图2.3-1,在平面直角坐标系中画出二次函数y=xr -12x+20 的图象,图象与 轴有两个交点,我们知道,这两个交点的横生标就是方程x -12x+20-0 的西个实数股
x=2.x=10. 因此二次函数y=x -12r+20 与:轴的两个交点是(2.0)和(10,0),
y-axr +bx+e >0)
的 图 象
= o
图2.3-1
直观想象 逻辑推理
ar +hx 的 根 +e-0(a>0) 有 根 两 个 不 相 等 的 实 数 xx(没 有 实 数 根
说教材——从方法论的角度分析
ax +hx+c<0(a>0) 的 解 集 (x|x因 为(x|2从具体到抽象
ax +hr+c>0(a>0)
的 解 集
归纳推理
类比建构
分类讨论
(x)xx )
2.3
o
R
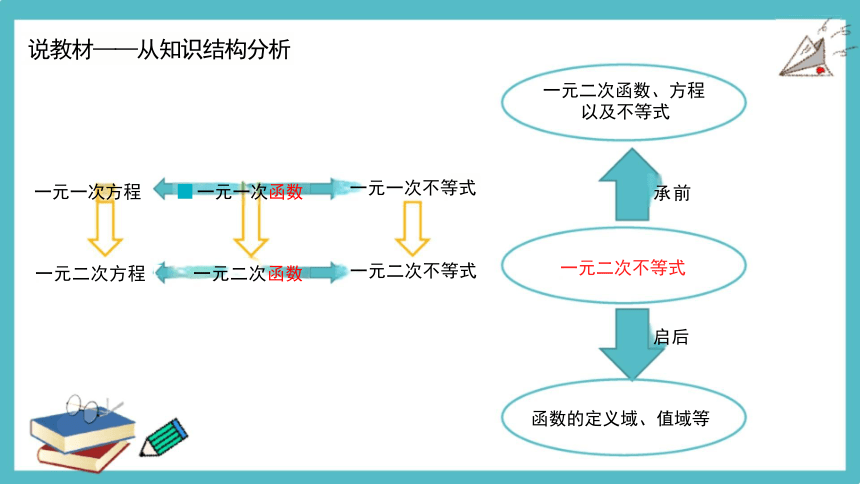
说教材——从知识结构分析
一元二次函数、方程 以及不等式
一元一次方程 ■ 一元一次函数
一元二次方程 一元二次函数
承前
一元二次不等式
启后
函数的定义域、值域等
一元一次不等式
一元二次不等式
《普通高中数学课程标准(2017年版2020 年修订)》对本节课的要求是:
①从函数的观点看一元二次不等式,经历从 实际情境中抽象出一元二次不等式的过程, 了解一元二次不等式的现实意义。
②能借助一元二次函数求解一元二次不等式, 并能用集合表示一元二次不等式的解集。
说教材——从课程标准分析
02
说学情
说学情
1.认知基础:
学生的知识储备:
初中阶段学生已经学习了一元一次方程, 一元一次函数和一元一次 不等式,知道这“三个一次”之间的关系,且掌握了一元二次方程的解 法和一元二次函数图象的画法。
学生的学习特点:
高中的学生基础知识比较扎实。对于知识具有较好的理解能力和应 用能力。他们更喜欢合作、探究式学习,对数学学习有较为浓厚的兴趣。 并且形成一定的直观想象能力和逻辑推理能力,数学抽象思维已有很大 发展,但还需依赖具体形象的内容理解抽象的逻辑关系。
说学情
2、认知困难:
函数与图象的应用是初中数学的难点,初中在此方面学习的 知识较为具体,因此学生对于数形结合的思想掌握不是很好。高 中阶段学生难以理解函数思想,较难直接把函数与方程和不等式 联系起来,所以在“三个二次”之间的联系上有一定的认知困难。
知识与技能目标
了解一元二次不等式的概念,以及一元二次 不等式在实际情境中的现实意义
掌握通过图象找一元二次方不等式解集的方 法,能运用一元二次不等式解决实际问题
理解二次函数的图象与一元二次方程的根、 一元二次不等式之间的整体与局部的关系
说教学目标
01
02
03
过程与方法目标
经历从实际情境抽象出一元二次不等式模型 的过程,让学生体会一元二次不等式的现实 意义以及数学模型抽象的过程
通过类比建构,从一次函数的观点看一元一 次方程、 一元一次不等式的思想方法,到从 二次函数的观点看一元二次方程、 一元二次 不等式,进而得到一元二次不等式的求解方 法。
01
说教学目标
02
借助图象,探究“二次函数”“一元二次方 程”“一元二次不等式”之间的整体与局部 的 关 系 ,感悟数形结合的思想方法
学生发展从特殊到一般,从整体到局部、由 具体到抽象的归纳概括能力,掌握一元二次 不等式的求解方法
过程与方法目标
说教学目标
03
04
在自主探究一元二次不等式的解法过程中激发学习数学 的热情,培养勇于探索的精神,学生体验成功的喜悦,树立 学习数学的自信心;培养合作交流意识,养成良好的数学学 习习惯。
情感态度与价值观
说教学目标
一元二次函数的图象与一元二次方程的根、 一元二次不等式之间的整体与局部的关系
重点 一元二次不等式的图象解法
教学重难点
说教学目标
难点
04
说教法学法
《普通高中数学课程标准》指出,数 学学科核心素养在学生与情境、问题的 有效互动中得到提升。
因此我们采用了问题驱动启发式结 构化教学法进行教学,以“问题串”的 形式引导学生动脑思考、动手操作、动 口表达,并且引导学生使用探究学习法 合作交流法、讨论法等学习方法探究一 元二次不等式的解法。
说教法学法
教法
学法
05
说教学过程
一元一次方程的根是一次函数图象与x轴交点 的横坐标
一元一次不等式的解集是一次函数图象在x轴 上(下)方时对应的x的取值范围
画出函数图象
构建“三个一次”的关系
y=ax+b(a>0)
0,b)
0
b
-
说教学过程
一、温故复习
ax+b>0
或ax+b<0(a≠0)
一元一次不等式
一元一次方程
一元一次函数
ax+b=0(a≠0)
y=ax+b(a≠0)
判别式△=b -4ac △>0 △=0 △<0
一元二次方程 ax +bc+c=0 的根 有两相异实数解 T ,x (T二次函数 y=ax +br+c 的图象
说教学过程
一元二次方程
一元二次函数
y=ax +bx+c(a≠0)
求解方法: 配方法 公式法 因式分解法
ax +bx+c=0(a≠ 0)
说教学过程
二、问题情境
园艺师打算在绿地上用栅栏围一个矩形区域种植花卉,若 栅栏的长度是24m, 围成的矩形区域的面积要大于20m ,则
这个矩形的边长为多少米
分析:长度→周长L=20m
面积→矩形面积S>20m
解:设这个矩形的边长为x m,则 另一条边长为(12-x)m
由题意得: (12- x)x>20, 其中0整理得: x -12x+20<0 矩形的边长要大于0,
所以要限定x 的取值 范围
先让学生自行思考,由算 术法不易得出答案,引导 学生设未知数列不等式求 解问题,题目问什么就设 什么
说教学过程
三、建构新知
一元二次不等式:只含有一个未知数,并且未知数的最 高次数是2的不等式.
例 :x -12x+20<0
-3x -10x+16>0
4x2+7x-9>0
一般形式: ax +bx+C>0 或ax +bx+c<0 (a,b,c均为常数,且a≠0)
提问学生,仿照一元一次不等 式的一般形式,让学生试着写 出一元二次不等式的一般形式, 让学生体会类比思想
问题情境列出题目所求一 元二次不等式后,引出一 元二次不等式的概念
说教学过程
四、拓展新知
零点: 对于二次函数y=ax +bx+c,我们把使ax +bx+c=0的实数x 叫做二次函数y=ax +bx+c的零点 .
通过一元二次函数图象和一元二次 方程的根,给学生讲解“函数的零 点”这一新知,让学生进一步理解 一元二次方程的根与一元二次函数 图象之间的局部与整体的关系。
一元二次方程x -12x+20=0的两根是 x =2和x =10
一元二次函数y=x -12x+20的零点是2和10
例 :
y=x -12x+20
(10,0)
(2,0)
说教学过程
四 、拓展新知
可以看出二次函数y=x -12x+20的两个零点x =2,x =10将x轴分成三段。
当x<2 或x>10 时,函数图像位于x轴上方,此时y>0 ,即x -12x+20>0; 当2所以, 一元二次不等式x -12x+20<0 的解集是
{x|2因为{x|2成的矩形的一条边长满足2的矩形区域面积大于20m 情况所要求范围
△>0 △=0
△<0
y=ax +br+c(a>0) 的图象 =
ar +bx+c=0(a>0) 的根 有两个不相等的实数 根x,x (x没有实数根
ar +hr+c>0(a>0) 的解集 (x |xx } xlx≠-
R
ar +hr+c<0(a>0) 的解集 {x|x说教学过程
四、拓展新知
“三个二次”的关系:
表2.3-1 二次函数与一元二次方程、不等式的解的对应关系
通过表格的形式,展现一元 二次方程、 一元二次函数和 一元二次不等式之间的“三 个二次”关系,培养学生的 逻辑知识体系,让学生感悟 数学中的整体与局部的思想。
说教学过程
五、学以致用
例:求下列不等式的解集.
x -5x+6>0 9x -6x>- 1
设计以上三道习题,求不同形式、不同 难度的一元二次不等式的解集。既提高 了学生逻辑推理的核心素养,又培养学 生解题时先分析后解答的好习惯。
-x +2x-3>0
说教学过程
六、归纳小结
解一元二次不等式的一般步骤:
1.化标准形式
2.算判别式
3.判实根
4.定零点,画草图
5.看图写解集
回顾课上解一元二次不等式的方法,让 学生自己归纳解一元二次不等式的一般 步骤。引导学生通过回忆本节新知探索 过程,理清其中所含的数学思想方法。
通过自己整理知识框架,做到复习回忆, 巩固新知。
06
说板书设计
问题情度
m
分朽: K=24m
本节课的板书分为六个板块,为教学过程的六个环节, 板书主次分明,重点突出,紧紧围绕教学目的展开。
而状
大度
△>0 △=0 △<0
有两个不相等 阴实友根×, 相
ax +bx+ (a>0)的国家
b =0 (ar0)
↓
y=ax+b(a≠0)
A×子b > 0
式ax+b< 0
ax b +c=0(a≠0)
y=ax tbx+C(aro)
②画y=×-12×+20
说板书设计
一、温放发习
1.-元-次方程
.①角方程:x-12X+20=0
a=6-4ac=+12) 4××~0=64>0
当x<2成×>10/R时,x-72xta>0
与2cxc10 时 .x -12×+20<0
2. 一元 方程
二次
S>2em
三个
=^ >0
6x十c=0有两个不相等 有两个相等 没有实根 a>0)的根的实根x石实教根
=■=
yaxbx+c
(a>0)的图豪 0 o
ax+b=(a
↓
y=ax+b(a≠; 三个一次
↓
ax+b0(a)
或 a x + b < 0
ax^2+bx+c=0(a≠0)
↓
y = a ^ 2 + 6 x 十 a ≠ 0
一、温放复习
1.一元一次方程
↓
一元一次函数
↓
一元一次不等式
2.一元二次方程
↓
一元二次医
说板书
x>10A时,X-12X+2>0
与2cX<10时 ,x -12X+2o<0
问题情境板块中,给出问题情境后,通过
分析后利用图形帮助学生理解题目意思。
说板书设计
4
建构新知板块中,帮助学生建构一 元二次不等式的概念,从思考到列 式,提出猜想、验证猜想,最后得 出一元二次不等式的求解过程。
两个不和等的文 有两十科等的了数
2 数核
t x l a , 减 x > -
(ln<<)
说板书设计
表1 二次昌数与一兄二次方程,不等式的解的时应关系
学以致用板块中,符合针对性原则, 板书中呈现了不同难度、不同类型 的题目、分析问题和解答过程,培 养学生养成先分析后解答的良好习 惯。
归纳小结板块中,以简单的记忆 口诀的形式,将本节课的重点呈 现出来,更便于学生理解记忆。
说板书设计
感谢观看
教材:
人教A版新课标高中数学必修一 第二章第三节第一课时
2.3二次函数与一元二次方程、不等式
说课
— —
说板书设计
说教学过程
说教法学法
说目标
03 04 05 06
目 录
说教材
说学情
02
01
在初中,我们从一次函数的角度看一元一次方程、 一元一 次不等式,发现了三者之间的内在联系,利用这种联系可以更 好地解决相关问题.对于二次函数、 一元二次方程和一元二次 不等式,是否也有这样的联系呢 先来看一个问题
问题 园艺师打算在绿地上用栅栏围一个矩形区域种
植花卉.若栅栏的长度是24 m, 围成的矩形区域的面积要
大于20 m , 则这个矩形的边长为多少米
设这个矩形的一条边长为x m, 则另 一条边长为
(12-x)m. 由题意,得
(12-x)x>20,
其中x ∈(x10
一般地,我们把只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元
二次不等式 (quadric inequality in one unknown),一元二次不等式的一般形式是 ax +bx+c>0 或ax +bx+c<0,
温故知新:三个一次之间的 关系,类比建构二次之间 的关系
情境导入:把实际问题抽象 为数学问题
建构新知:类比一元一次不 等式的概念建构一元二次不 等式的概念
2.3 二次函数与一元二次方程、不等式
说教材——简述教材内容
其中a,b,c 均为常数,a≠0.
y=ar +br+c 的零点.于是,二次函数y=x -12x+20 的两个零点是x =2,x =10.
从图2.3-1可以看出,二次函数y=x -12x+20 的两 个零点x =2.x =10 将x 轴分成三段.相应地,当x<2 或x>10 时,函数图象位于x 轴上方,此时y>0, 即 x -
12x+20>0; 当 2
② 思考
在初中,我们学习了从一次函数的观点看一元一次方程、 一元一次不等式的思想
方法。类似地,能否从二次函数的观点看一元二次不等式,进而得到一元二次不等式 的求解方法呢
下面,我们先考察一元二次不等式x -12x+20<0 与二次函数y=x -12x+20 之 间的关系.
如图2.3-1,在平面直角坐标系中画出二次函数y=x -1 2x+20 的图象,图象与x 轴有两个交点,我们知道,这两个交点的横坐标就是方程x -12r+20=0 的两个实数根
x =2,x =10, 因此二次函数y=x -12 r+20 与x 轴的两个交点是(2,0)和(10,0).
一般地,对于二次函数y=ax +br+c, 我们把使ax +bx+c=0 的实数x 叫做二次函数
说教材——简述教材内容
启发:引导学生类比三个一 次之间的关系来思考一元二 次不等式解集的求解方法
y=x -12x+20
10
o 25 5 0x
-10
-1s
图2.3-1
△>0 △=0
△<0
y=ax +bx+c(a>0) 的图象 0x =
ax +br+c-0(a>0) 的根 有两个不相等的实数 根 x , r ( x < x ) 有两个相等的实数根 x=x=-
没有实数根
ax +bx+c>0(a>0) 的解集 (x |x
R
ar +bx+c<0(a>0) 的解集 (x|x
得到x -5x+6>0 的解集。
例 2 求不等式9x -6x+1>0
例 3 求不等式-x +2x-3>0
说教材——简述教材内容
表2.3-1 二次函数与一元二次方程、不等式的解的对应关系
巩固:设计三道习题对一元二次 不等式的新知进行巩固练习
例 1 求不等式x -5x+6>0 分析:因为方程x -5x+6=0 的零点,所以先求出x -5r+6=0 的解集.
的根是函数y=x -5x+6
的根,再根据函数图象
的解集.
的解集.
二次函数与一元二次方程、不等式
② 思考
在初中。我们学习了从一次函数的观点看一元一次方程、 一无一次不等式的思想 方法。类假地,能否从二次温数的观点看一元二次不等式,进而得列一元二次不等式 的求解方进呢
从特殊到 一 般
表2 . 3 - 1 二次函数与 一 元二次方程、不等式的解的对应关系
△>0 △=0 △<0
一般地,对于二次函数s=ar +hr+, 我们把陵a +hur+r=0 y-ar +br+c 的零点,于是,二次函数y-x -12x+20 的两个零点是x =2.x =10. 从图2.3-1可以看出,二次函数y=x -12x+20 的 两 个零点x =2,x =10 将 x 轴分成三段.相应地,当x< 或 x>10 时,函数图象位于x 输上方,此时y>0, 即 x - 12x+20>0; 当 2
0
s 5
1 -15
在p, 表以一次函数的角度看一一次方程, 一元一 次不等式,发现了三者之间的内在联6.和用这和联系问以更 好地解次相关月对于二次涵数, 一元二次方程和一元二次 不等式,是否也有这样系 先来看一个施
构 园艺师打算在绿地上用槽把围一十能形区域种
植花本者棚栏的长度是24m. 围或的矩形区域的百积要
大于 m, 州这个短形的边长为多夕料
设这个证形的一身边长为xm. 州另一条应长为
(12-x)n. 由题意,得
其中x610<<12). 想
x -12r+20C0.xtu10
一程地。我们把只含有一个未数。并具未知数的最高次营是2的不等式,称为一元 二次不等式(quslik ineumlyiso akamn,一K 二次不等式的一血形式是
ax '+btc>0 成ax tàrta<0,
其中。,A., 均为营数.az0
下面,我们先考察一元二次不等式x -12x+20<0 与二次函数y-x -12x+20 之
如图2.3-1,在平面直角坐标系中画出二次函数y=xr -12x+20 的图象,图象与 轴有两个交点,我们知道,这两个交点的横生标就是方程x -12x+20-0 的西个实数股
x=2.x=10. 因此二次函数y=x -12r+20 与:轴的两个交点是(2.0)和(10,0),
y-axr +bx+e >0)
的 图 象
= o
图2.3-1
直观想象 逻辑推理
ar +hx 的 根 +e-0(a>0) 有 根 两 个 不 相 等 的 实 数 xx(
说教材——从方法论的角度分析
ax +hx+c<0(a>0) 的 解 集 (x|x
ax +hr+c>0(a>0)
的 解 集
归纳推理
类比建构
分类讨论
(x)x
2.3
o
R
说教材——从知识结构分析
一元二次函数、方程 以及不等式
一元一次方程 ■ 一元一次函数
一元二次方程 一元二次函数
承前
一元二次不等式
启后
函数的定义域、值域等
一元一次不等式
一元二次不等式
《普通高中数学课程标准(2017年版2020 年修订)》对本节课的要求是:
①从函数的观点看一元二次不等式,经历从 实际情境中抽象出一元二次不等式的过程, 了解一元二次不等式的现实意义。
②能借助一元二次函数求解一元二次不等式, 并能用集合表示一元二次不等式的解集。
说教材——从课程标准分析
02
说学情
说学情
1.认知基础:
学生的知识储备:
初中阶段学生已经学习了一元一次方程, 一元一次函数和一元一次 不等式,知道这“三个一次”之间的关系,且掌握了一元二次方程的解 法和一元二次函数图象的画法。
学生的学习特点:
高中的学生基础知识比较扎实。对于知识具有较好的理解能力和应 用能力。他们更喜欢合作、探究式学习,对数学学习有较为浓厚的兴趣。 并且形成一定的直观想象能力和逻辑推理能力,数学抽象思维已有很大 发展,但还需依赖具体形象的内容理解抽象的逻辑关系。
说学情
2、认知困难:
函数与图象的应用是初中数学的难点,初中在此方面学习的 知识较为具体,因此学生对于数形结合的思想掌握不是很好。高 中阶段学生难以理解函数思想,较难直接把函数与方程和不等式 联系起来,所以在“三个二次”之间的联系上有一定的认知困难。
知识与技能目标
了解一元二次不等式的概念,以及一元二次 不等式在实际情境中的现实意义
掌握通过图象找一元二次方不等式解集的方 法,能运用一元二次不等式解决实际问题
理解二次函数的图象与一元二次方程的根、 一元二次不等式之间的整体与局部的关系
说教学目标
01
02
03
过程与方法目标
经历从实际情境抽象出一元二次不等式模型 的过程,让学生体会一元二次不等式的现实 意义以及数学模型抽象的过程
通过类比建构,从一次函数的观点看一元一 次方程、 一元一次不等式的思想方法,到从 二次函数的观点看一元二次方程、 一元二次 不等式,进而得到一元二次不等式的求解方 法。
01
说教学目标
02
借助图象,探究“二次函数”“一元二次方 程”“一元二次不等式”之间的整体与局部 的 关 系 ,感悟数形结合的思想方法
学生发展从特殊到一般,从整体到局部、由 具体到抽象的归纳概括能力,掌握一元二次 不等式的求解方法
过程与方法目标
说教学目标
03
04
在自主探究一元二次不等式的解法过程中激发学习数学 的热情,培养勇于探索的精神,学生体验成功的喜悦,树立 学习数学的自信心;培养合作交流意识,养成良好的数学学 习习惯。
情感态度与价值观
说教学目标
一元二次函数的图象与一元二次方程的根、 一元二次不等式之间的整体与局部的关系
重点 一元二次不等式的图象解法
教学重难点
说教学目标
难点
04
说教法学法
《普通高中数学课程标准》指出,数 学学科核心素养在学生与情境、问题的 有效互动中得到提升。
因此我们采用了问题驱动启发式结 构化教学法进行教学,以“问题串”的 形式引导学生动脑思考、动手操作、动 口表达,并且引导学生使用探究学习法 合作交流法、讨论法等学习方法探究一 元二次不等式的解法。
说教法学法
教法
学法
05
说教学过程
一元一次方程的根是一次函数图象与x轴交点 的横坐标
一元一次不等式的解集是一次函数图象在x轴 上(下)方时对应的x的取值范围
画出函数图象
构建“三个一次”的关系
y=ax+b(a>0)
0,b)
0
b
-
说教学过程
一、温故复习
ax+b>0
或ax+b<0(a≠0)
一元一次不等式
一元一次方程
一元一次函数
ax+b=0(a≠0)
y=ax+b(a≠0)
判别式△=b -4ac △>0 △=0 △<0
一元二次方程 ax +bc+c=0 的根 有两相异实数解 T ,x (T
说教学过程
一元二次方程
一元二次函数
y=ax +bx+c(a≠0)
求解方法: 配方法 公式法 因式分解法
ax +bx+c=0(a≠ 0)
说教学过程
二、问题情境
园艺师打算在绿地上用栅栏围一个矩形区域种植花卉,若 栅栏的长度是24m, 围成的矩形区域的面积要大于20m ,则
这个矩形的边长为多少米
分析:长度→周长L=20m
面积→矩形面积S>20m
解:设这个矩形的边长为x m,则 另一条边长为(12-x)m
由题意得: (12- x)x>20, 其中0
所以要限定x 的取值 范围
先让学生自行思考,由算 术法不易得出答案,引导 学生设未知数列不等式求 解问题,题目问什么就设 什么
说教学过程
三、建构新知
一元二次不等式:只含有一个未知数,并且未知数的最 高次数是2的不等式.
例 :x -12x+20<0
-3x -10x+16>0
4x2+7x-9>0
一般形式: ax +bx+C>0 或ax +bx+c<0 (a,b,c均为常数,且a≠0)
提问学生,仿照一元一次不等 式的一般形式,让学生试着写 出一元二次不等式的一般形式, 让学生体会类比思想
问题情境列出题目所求一 元二次不等式后,引出一 元二次不等式的概念
说教学过程
四、拓展新知
零点: 对于二次函数y=ax +bx+c,我们把使ax +bx+c=0的实数x 叫做二次函数y=ax +bx+c的零点 .
通过一元二次函数图象和一元二次 方程的根,给学生讲解“函数的零 点”这一新知,让学生进一步理解 一元二次方程的根与一元二次函数 图象之间的局部与整体的关系。
一元二次方程x -12x+20=0的两根是 x =2和x =10
一元二次函数y=x -12x+20的零点是2和10
例 :
y=x -12x+20
(10,0)
(2,0)
说教学过程
四 、拓展新知
可以看出二次函数y=x -12x+20的两个零点x =2,x =10将x轴分成三段。
当x<2 或x>10 时,函数图像位于x轴上方,此时y>0 ,即x -12x+20>0; 当2
{x|2
△>0 △=0
△<0
y=ax +br+c(a>0) 的图象 =
ar +bx+c=0(a>0) 的根 有两个不相等的实数 根x,x (x
ar +hr+c>0(a>0) 的解集 (x |x
R
ar +hr+c<0(a>0) 的解集 {x|x
四、拓展新知
“三个二次”的关系:
表2.3-1 二次函数与一元二次方程、不等式的解的对应关系
通过表格的形式,展现一元 二次方程、 一元二次函数和 一元二次不等式之间的“三 个二次”关系,培养学生的 逻辑知识体系,让学生感悟 数学中的整体与局部的思想。
说教学过程
五、学以致用
例:求下列不等式的解集.
x -5x+6>0 9x -6x>- 1
设计以上三道习题,求不同形式、不同 难度的一元二次不等式的解集。既提高 了学生逻辑推理的核心素养,又培养学 生解题时先分析后解答的好习惯。
-x +2x-3>0
说教学过程
六、归纳小结
解一元二次不等式的一般步骤:
1.化标准形式
2.算判别式
3.判实根
4.定零点,画草图
5.看图写解集
回顾课上解一元二次不等式的方法,让 学生自己归纳解一元二次不等式的一般 步骤。引导学生通过回忆本节新知探索 过程,理清其中所含的数学思想方法。
通过自己整理知识框架,做到复习回忆, 巩固新知。
06
说板书设计
问题情度
m
分朽: K=24m
本节课的板书分为六个板块,为教学过程的六个环节, 板书主次分明,重点突出,紧紧围绕教学目的展开。
而状
大度
△>0 △=0 △<0
有两个不相等 阴实友根×, 相
ax +bx+ (a>0)的国家
b =0 (ar0)
↓
y=ax+b(a≠0)
A×子b > 0
式ax+b< 0
ax b +c=0(a≠0)
y=ax tbx+C(aro)
②画y=×-12×+20
说板书设计
一、温放发习
1.-元-次方程
.①角方程:x-12X+20=0
a=6-4ac=+12) 4××~0=64>0
当x<2成×>10/R时,x-72xta>0
与2cxc10 时 .x -12×+20<0
2. 一元 方程
二次
S>2em
三个
=^ >0
6x十c=0有两个不相等 有两个相等 没有实根 a>0)的根的实根x石实教根
=■=
yaxbx+c
(a>0)的图豪 0 o
ax+b=(a
↓
y=ax+b(a≠; 三个一次
↓
ax+b0(a)
或 a x + b < 0
ax^2+bx+c=0(a≠0)
↓
y = a ^ 2 + 6 x 十 a ≠ 0
一、温放复习
1.一元一次方程
↓
一元一次函数
↓
一元一次不等式
2.一元二次方程
↓
一元二次医
说板书
x>10A时,X-12X+2>0
与2cX<10时 ,x -12X+2o<0
问题情境板块中,给出问题情境后,通过
分析后利用图形帮助学生理解题目意思。
说板书设计
4
建构新知板块中,帮助学生建构一 元二次不等式的概念,从思考到列 式,提出猜想、验证猜想,最后得 出一元二次不等式的求解过程。
两个不和等的文 有两十科等的了数
2 数核
t x l a , 减 x > -
(ln<<)
说板书设计
表1 二次昌数与一兄二次方程,不等式的解的时应关系
学以致用板块中,符合针对性原则, 板书中呈现了不同难度、不同类型 的题目、分析问题和解答过程,培 养学生养成先分析后解答的良好习 惯。
归纳小结板块中,以简单的记忆 口诀的形式,将本节课的重点呈 现出来,更便于学生理解记忆。
说板书设计
感谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
