第1、2单元练习题(试题)-2023-2024学年五年级下册数学人教版(无答案)
文档属性
| 名称 | 第1、2单元练习题(试题)-2023-2024学年五年级下册数学人教版(无答案) | 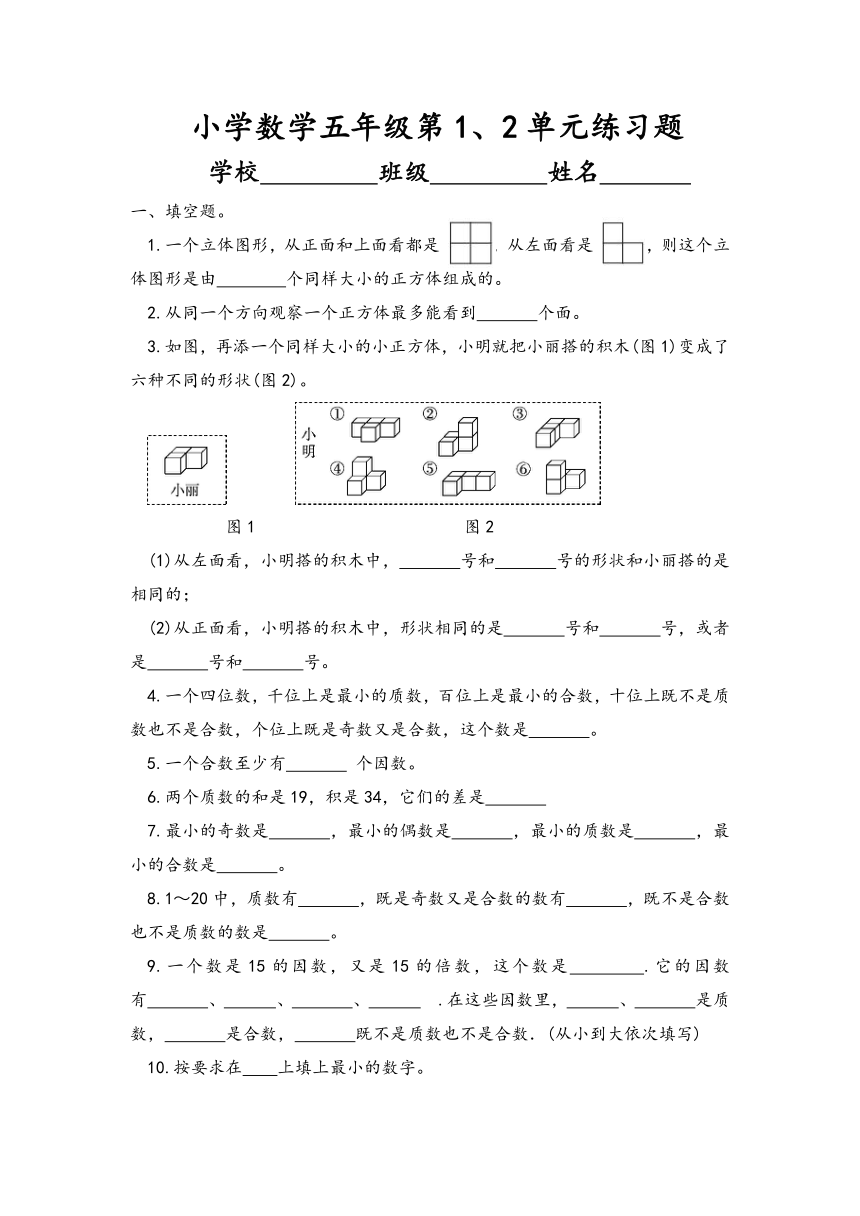 | |
| 格式 | docx | ||
| 文件大小 | 35.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-30 14:02:35 | ||
图片预览


文档简介
小学数学五年级第1、2单元练习题
学校 班级 姓名
一、填空题。
1.一个立体图形,从正面和上面看都是 ,从左面看是 ,则这个立体图形是由 个同样大小的正方体组成的。
2.从同一个方向观察一个正方体最多能看到 个面。
3.如图,再添一个同样大小的小正方体,小明就把小丽搭的积木(图1)变成了六种不同的形状(图2)。
图1 图2
(1)从左面看,小明搭的积木中, 号和 号的形状和小丽搭的是相同的;
(2)从正面看,小明搭的积木中,形状相同的是 号和 号,或者是 号和 号。
4.一个四位数,千位上是最小的质数,百位上是最小的合数,十位上既不是质数也不是合数,个位上既是奇数又是合数,这个数是 。
5.一个合数至少有 个因数。
6.两个质数的和是19,积是34,它们的差是
7.最小的奇数是 ,最小的偶数是 ,最小的质数是 ,最小的合数是 。
8.1~20中,质数有 ,既是奇数又是合数的数有 ,既不是合数也不是质数的数是 。
9.一个数是15的因数,又是15的倍数,这个数是 .它的因数有 、 、 、 .在这些因数里, 、 是质数, 是合数, 既不是质数也不是合数.(从小到大依次填写)
10.按要求在 上填上最小的数字。
(1)26 (2和3的倍数)
(2)183 (2和5的倍数)
(3)30 5(3和5的倍数)
(4)7 9 (2,3和5的倍数)
二、判断题。(正确的画“√”,错误的画“ ”)
1.由相同个数的正方体摆成的物体从上面看的图形都是相同的。 ( )
2.由3个 拼成一个物体,从正面看到的是 ,那么这3个 只有2种摆法。 ( )
3.一个自然数越小,它的因数个数越少。 ( )
4.质数加质数得奇数。 ( )
5.除了2以外,所有的质数都是奇数。 ( )
6.因为3×7=21,所以3是因数,21是倍数。 ( )
7.如果一个数是6的倍数,那么它一定是2和3的倍数。 ( )
三、选择题。(把正确答案的序号填在括号里)
1.如图,它是由6个同样大小的正方体摆成的几何体。将正方体①移走后,从正面、上面和左面观察新几何体与从正面、上面和左面观察原几何体相比,下列说法正确的是( )。
A.从正面看到的图形没有发生改变
B.从上面看到的图形没有发生改变
C.从左面看到的图形没有发生改变
D.从任何一面看到的图形都发生了改变
2.一个立体图形由6个同样大小的正方体组成,从左面看形状是 ,从上面看形状是 ,共有( )种不同的搭法。
A.3 B.6
C.7 D.8
3.小刚搭的积木从上面看到的形状是,积木上的数表示在这个位置上所用小正方体的个数。从正面看是( ),从左面看是( )。
4.若a+7的和是奇数,则a一定是( )。
A.奇数 B.质数
C.合数 D.偶数
5当m是非0的自然数时,2m-1一定是( )。
A.奇数 B.偶数
C.奇数或偶数 D.不能确定
6.下列说法中,有( )个是正确的。
①一个数的最小的倍数是它本身 ②0是最小的自然数
③一个数至少有两个因数 ④各个数位上数字的和是9的倍数,这个数就是9的倍数
A.1 B.2
C.3 D.4
把下列各数进行分类。
13 20 1 45 38 0 2 91 37 57 80
五、从四张卡片中选出三张,按要求组成一个三位数,使它符合题目要求。
(
6
0
3
5
)
1.奇数:__________________
2.偶数:__________________
3.3的倍数:__________________
4.5的倍数:__________________
既是3的倍数,又是5的倍数:__________
同时是2,3,5的倍数:____________
六、解决问题。
1.小明家无线网的密码是一个六位数。第一位数既是偶数又是质数,第二位数既是4的倍数又是4的因数,第三位数既是奇数又是合数,第四位数既不是质数也不是合数也不是0,第五位数是8的最小因数,最后一位数是最小的自然数。小明家无线网的密码是多少?
2.一个长方形的长和宽都是以厘米为单位的质数,并且周长是36 cm。这个长方形的面积最大是多少平方厘米?
3.天天到文具店买日记本,他买了3本相同的日记本,单价是整数元,售货员阿姨说应付28元。售货员阿姨算的对不对?为什么?
小船最初在南岸,从南岸驶向北岸,再从北岸驶回南岸,不断往返
(往返算2次)。
(1) 小船摆渡11次后在南岸还是在北岸?为什么?
(2) 有人说摆渡100次后,小船在北岸,他的说法对吗?为什么?
学校 班级 姓名
一、填空题。
1.一个立体图形,从正面和上面看都是 ,从左面看是 ,则这个立体图形是由 个同样大小的正方体组成的。
2.从同一个方向观察一个正方体最多能看到 个面。
3.如图,再添一个同样大小的小正方体,小明就把小丽搭的积木(图1)变成了六种不同的形状(图2)。
图1 图2
(1)从左面看,小明搭的积木中, 号和 号的形状和小丽搭的是相同的;
(2)从正面看,小明搭的积木中,形状相同的是 号和 号,或者是 号和 号。
4.一个四位数,千位上是最小的质数,百位上是最小的合数,十位上既不是质数也不是合数,个位上既是奇数又是合数,这个数是 。
5.一个合数至少有 个因数。
6.两个质数的和是19,积是34,它们的差是
7.最小的奇数是 ,最小的偶数是 ,最小的质数是 ,最小的合数是 。
8.1~20中,质数有 ,既是奇数又是合数的数有 ,既不是合数也不是质数的数是 。
9.一个数是15的因数,又是15的倍数,这个数是 .它的因数有 、 、 、 .在这些因数里, 、 是质数, 是合数, 既不是质数也不是合数.(从小到大依次填写)
10.按要求在 上填上最小的数字。
(1)26 (2和3的倍数)
(2)183 (2和5的倍数)
(3)30 5(3和5的倍数)
(4)7 9 (2,3和5的倍数)
二、判断题。(正确的画“√”,错误的画“ ”)
1.由相同个数的正方体摆成的物体从上面看的图形都是相同的。 ( )
2.由3个 拼成一个物体,从正面看到的是 ,那么这3个 只有2种摆法。 ( )
3.一个自然数越小,它的因数个数越少。 ( )
4.质数加质数得奇数。 ( )
5.除了2以外,所有的质数都是奇数。 ( )
6.因为3×7=21,所以3是因数,21是倍数。 ( )
7.如果一个数是6的倍数,那么它一定是2和3的倍数。 ( )
三、选择题。(把正确答案的序号填在括号里)
1.如图,它是由6个同样大小的正方体摆成的几何体。将正方体①移走后,从正面、上面和左面观察新几何体与从正面、上面和左面观察原几何体相比,下列说法正确的是( )。
A.从正面看到的图形没有发生改变
B.从上面看到的图形没有发生改变
C.从左面看到的图形没有发生改变
D.从任何一面看到的图形都发生了改变
2.一个立体图形由6个同样大小的正方体组成,从左面看形状是 ,从上面看形状是 ,共有( )种不同的搭法。
A.3 B.6
C.7 D.8
3.小刚搭的积木从上面看到的形状是,积木上的数表示在这个位置上所用小正方体的个数。从正面看是( ),从左面看是( )。
4.若a+7的和是奇数,则a一定是( )。
A.奇数 B.质数
C.合数 D.偶数
5当m是非0的自然数时,2m-1一定是( )。
A.奇数 B.偶数
C.奇数或偶数 D.不能确定
6.下列说法中,有( )个是正确的。
①一个数的最小的倍数是它本身 ②0是最小的自然数
③一个数至少有两个因数 ④各个数位上数字的和是9的倍数,这个数就是9的倍数
A.1 B.2
C.3 D.4
把下列各数进行分类。
13 20 1 45 38 0 2 91 37 57 80
五、从四张卡片中选出三张,按要求组成一个三位数,使它符合题目要求。
(
6
0
3
5
)
1.奇数:__________________
2.偶数:__________________
3.3的倍数:__________________
4.5的倍数:__________________
既是3的倍数,又是5的倍数:__________
同时是2,3,5的倍数:____________
六、解决问题。
1.小明家无线网的密码是一个六位数。第一位数既是偶数又是质数,第二位数既是4的倍数又是4的因数,第三位数既是奇数又是合数,第四位数既不是质数也不是合数也不是0,第五位数是8的最小因数,最后一位数是最小的自然数。小明家无线网的密码是多少?
2.一个长方形的长和宽都是以厘米为单位的质数,并且周长是36 cm。这个长方形的面积最大是多少平方厘米?
3.天天到文具店买日记本,他买了3本相同的日记本,单价是整数元,售货员阿姨说应付28元。售货员阿姨算的对不对?为什么?
小船最初在南岸,从南岸驶向北岸,再从北岸驶回南岸,不断往返
(往返算2次)。
(1) 小船摆渡11次后在南岸还是在北岸?为什么?
(2) 有人说摆渡100次后,小船在北岸,他的说法对吗?为什么?
