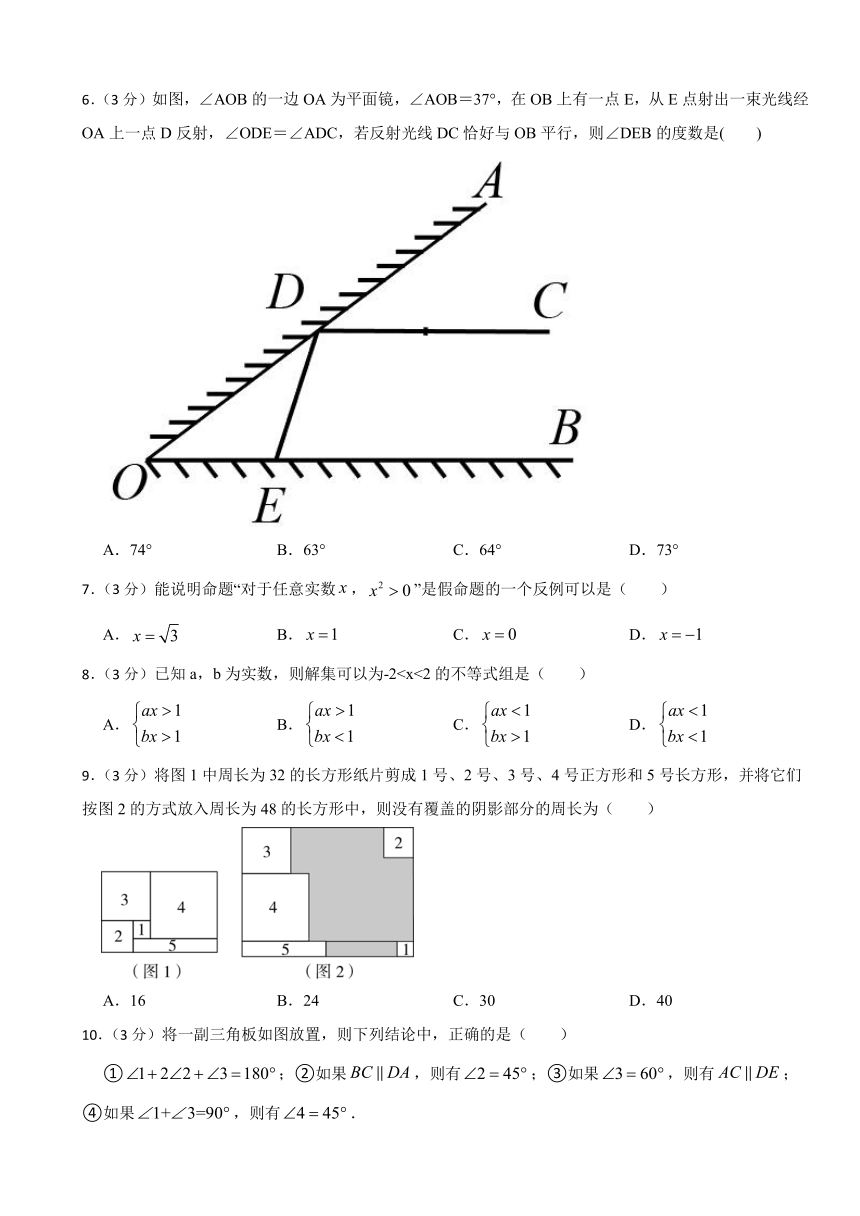
2023-2024学年七年级下学期人教版数学期末提升训练(含简单答案)
文档属性
| 名称 | 2023-2024学年七年级下学期人教版数学期末提升训练(含简单答案) |  | |
| 格式 | docx | ||
| 文件大小 | 323.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-30 16:06:11 | ||
图片预览


文档简介
2023-2024学年七年级下学期人教版数学期末提升训练
一、单选题(共10题;共30分)
1.(3分)某校图书管理员清理阅览室的课外书籍时,将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图,已知甲类书有30本,则丙类书的本数是( )
A.90 B.144 C.200 D.80
2.(3分)湿地公园位于学校北偏西方向处,下列选项中表示正确的是( )
A. B.
C. D.
3.(3分)已知,要使,则( )
A. B. C. D.为任意数
4.(3分)把不等式组的解集表示在数轴上,下列选项正确的是( )
A. B.
C. D.
5.(3分)已知,则下列各式中一定成立的是( )
A. B.
C. D.
6.(3分)如图,∠AOB的一边OA为平面镜,∠AOB=37°,在OB上有一点E,从E点射出一束光线经OA上一点D反射,∠ODE=∠ADC,若反射光线DC恰好与OB平行,则∠DEB的度数是( )
A.74° B.63° C.64° D.73°
7.(3分)能说明命题“对于任意实数,”是假命题的一个反例可以是( )
A. B. C. D.
8.(3分)已知a,b为实数,则解集可以为-2A. B. C. D.
9.(3分)将图1中周长为32的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形,并将它们按图2的方式放入周长为48的长方形中,则没有覆盖的阴影部分的周长为( )
A.16 B.24 C.30 D.40
10.(3分)将一副三角板如图放置,则下列结论中,正确的是( )
①;②如果,则有;③如果,则有;④如果,则有.
A.①②③④ B.③④ C.①②④ D.①②③
二、填空题(共6题;共21分)
11.(3分)中国清代学者华衡芳和英国人傅兰雅合译英国瓦里斯的《代数学》,卷首有“代数之法,无论何数,皆可以任何记号代之”,说明了所谓“代数”,就是用符号来代表数的一种方法.若一个正数的平方根分别是2a-1和-a+2,则这个正数是 .
12.(3分)将实数﹣ , ,π,﹣ 按从小到大的顺序排列,并用“<”连接: .
13.(3分)设a,b是两个连续的整数,已知 是一个无理数,若 ,是,则 = .
14.(3分)已知不等式的正整数解恰好是1、2、3,则的取值范围是 .
15.(3分)若关于x的不等式恰有三个整数解,则,实数a的取值范围是 .
16.(6分)在平面直角坐标系 中,我们把横 、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
三、解答题(共7题;共49分)
17.(6分)计算:|π﹣3|+( )2+( ﹣1)0.
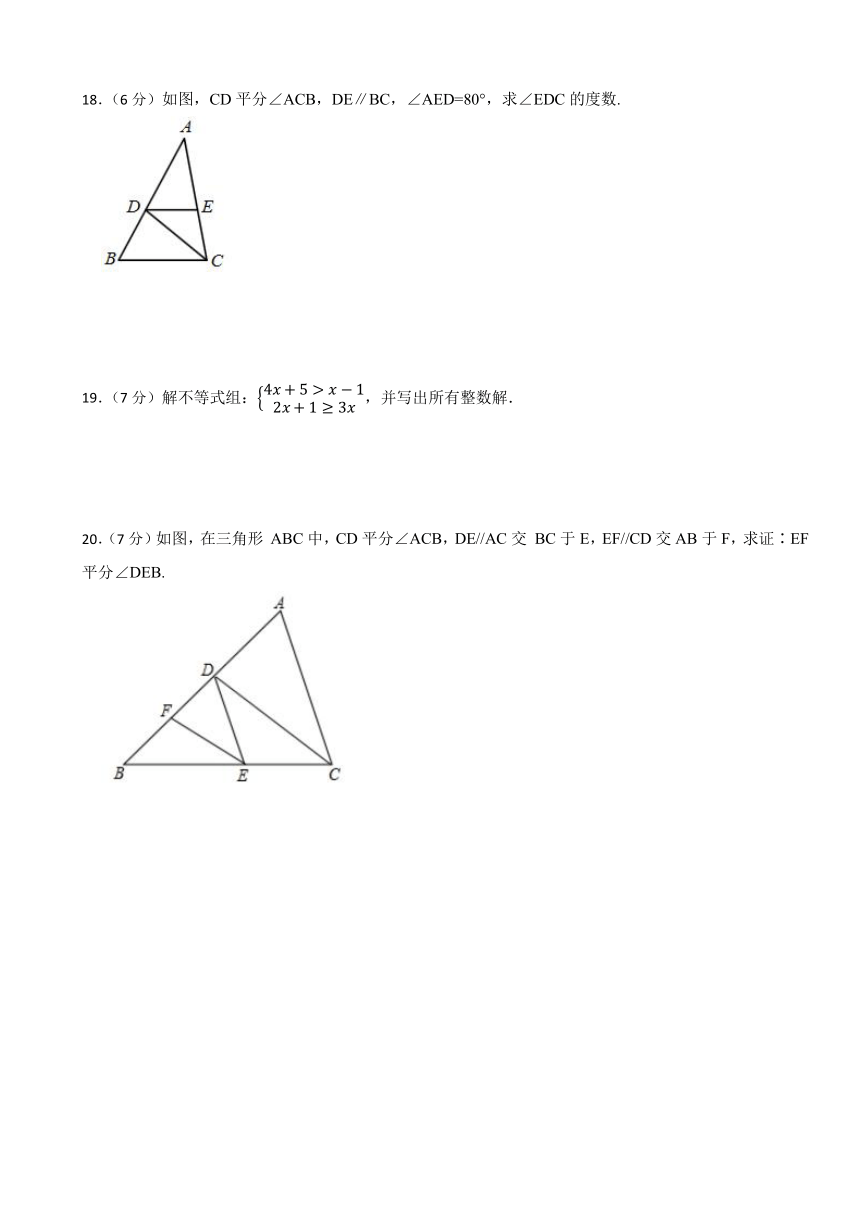
18.(6分)如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠EDC的度数.
19.(7分)解不等式组:,并写出所有整数解.
20.(7分)如图,在三角形 ABC中,CD平分∠ACB,DE//AC交 BC于E,EF//CD交AB于F,求证∶EF平分∠DEB.
21.(7分)阅读以下例题:解不等式:
解:①当,则
即可以写成:,解不等式组得:
②当若,则
即可以写成:解不等式组得:
综合以上两种情况:不等式解集:或.
以上解法的依据为:当,则,或,
(1)(3分)若,则,b______0或,b______0
(2)(4分)请你模仿例题的解法,解不等式:
①;
②.
22.(8分)如图,在折线中,已知,延长、交于点,猜想与的关系,并说明理由.
23.(8分)对于平面直角坐标系中的图形G和点P,给出如下定义:将图形G沿上、下、左、右四个方向中的任意一个方向平移一次,平移距离小于或者等于1个单位长度,平移后的图形记为,若点P在图形上,则称点P为图形G的稳定点,例如,当图形G为点时,点都是图形G的稳定点.
(1)(4分)已知点.
①在点中,线段的稳定点是___________.
②若将线段向上平移t个单位长度,使得点或者点为线段的稳定点,写出t的取值范围___________.
(2)(4分)边长为a的正方形,一个顶点是原点O,相邻两边分别在x轴、y轴的正半轴上,这个正方形及其内部记为图形G.若以为端点的线段上的所有点都是这个图形G的稳定点,直接写出a的最小值___________.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】A
4.【答案】B
5.【答案】B
6.【答案】A
7.【答案】C
8.【答案】D
9.【答案】D
10.【答案】D
11.【答案】9
12.【答案】﹣ <﹣ < <π
13.【答案】9
14.【答案】9≤a<12
15.【答案】或
16.【答案】3或4;6n-3
17.【答案】解:原式 .
18.【答案】40°
19.【答案】;不等式组的所有整数解是:,0,1
20.【答案】证明:CD平分∠ACB,
∴∠ACD=∠DCB,
∵DE//AC,EF//CD,
∴∠ACD=∠EDC,∠FED=∠EDC,∠BEF=∠DCB
∴∠ACD=∠FED=∠DCB=∠BEF,
∴EF平分∠DEB.
21.【答案】(1)<;>
(2)①或;②
22.【答案】解:.理由如下:
延长交于点,
因为,
所以,
所以,
又,
所以,
所以,
所以.
.
23.【答案】(1)①,;②0≤t≤2或4≤t≤6;
(2)3
一、单选题(共10题;共30分)
1.(3分)某校图书管理员清理阅览室的课外书籍时,将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图,已知甲类书有30本,则丙类书的本数是( )
A.90 B.144 C.200 D.80
2.(3分)湿地公园位于学校北偏西方向处,下列选项中表示正确的是( )
A. B.
C. D.
3.(3分)已知,要使,则( )
A. B. C. D.为任意数
4.(3分)把不等式组的解集表示在数轴上,下列选项正确的是( )
A. B.
C. D.
5.(3分)已知,则下列各式中一定成立的是( )
A. B.
C. D.
6.(3分)如图,∠AOB的一边OA为平面镜,∠AOB=37°,在OB上有一点E,从E点射出一束光线经OA上一点D反射,∠ODE=∠ADC,若反射光线DC恰好与OB平行,则∠DEB的度数是( )
A.74° B.63° C.64° D.73°
7.(3分)能说明命题“对于任意实数,”是假命题的一个反例可以是( )
A. B. C. D.
8.(3分)已知a,b为实数,则解集可以为-2
9.(3分)将图1中周长为32的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形,并将它们按图2的方式放入周长为48的长方形中,则没有覆盖的阴影部分的周长为( )
A.16 B.24 C.30 D.40
10.(3分)将一副三角板如图放置,则下列结论中,正确的是( )
①;②如果,则有;③如果,则有;④如果,则有.
A.①②③④ B.③④ C.①②④ D.①②③
二、填空题(共6题;共21分)
11.(3分)中国清代学者华衡芳和英国人傅兰雅合译英国瓦里斯的《代数学》,卷首有“代数之法,无论何数,皆可以任何记号代之”,说明了所谓“代数”,就是用符号来代表数的一种方法.若一个正数的平方根分别是2a-1和-a+2,则这个正数是 .
12.(3分)将实数﹣ , ,π,﹣ 按从小到大的顺序排列,并用“<”连接: .
13.(3分)设a,b是两个连续的整数,已知 是一个无理数,若 ,是,则 = .
14.(3分)已知不等式的正整数解恰好是1、2、3,则的取值范围是 .
15.(3分)若关于x的不等式恰有三个整数解,则,实数a的取值范围是 .
16.(6分)在平面直角坐标系 中,我们把横 、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
三、解答题(共7题;共49分)
17.(6分)计算:|π﹣3|+( )2+( ﹣1)0.
18.(6分)如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠EDC的度数.
19.(7分)解不等式组:,并写出所有整数解.
20.(7分)如图,在三角形 ABC中,CD平分∠ACB,DE//AC交 BC于E,EF//CD交AB于F,求证∶EF平分∠DEB.
21.(7分)阅读以下例题:解不等式:
解:①当,则
即可以写成:,解不等式组得:
②当若,则
即可以写成:解不等式组得:
综合以上两种情况:不等式解集:或.
以上解法的依据为:当,则,或,
(1)(3分)若,则,b______0或,b______0
(2)(4分)请你模仿例题的解法,解不等式:
①;
②.
22.(8分)如图,在折线中,已知,延长、交于点,猜想与的关系,并说明理由.
23.(8分)对于平面直角坐标系中的图形G和点P,给出如下定义:将图形G沿上、下、左、右四个方向中的任意一个方向平移一次,平移距离小于或者等于1个单位长度,平移后的图形记为,若点P在图形上,则称点P为图形G的稳定点,例如,当图形G为点时,点都是图形G的稳定点.
(1)(4分)已知点.
①在点中,线段的稳定点是___________.
②若将线段向上平移t个单位长度,使得点或者点为线段的稳定点,写出t的取值范围___________.
(2)(4分)边长为a的正方形,一个顶点是原点O,相邻两边分别在x轴、y轴的正半轴上,这个正方形及其内部记为图形G.若以为端点的线段上的所有点都是这个图形G的稳定点,直接写出a的最小值___________.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】A
4.【答案】B
5.【答案】B
6.【答案】A
7.【答案】C
8.【答案】D
9.【答案】D
10.【答案】D
11.【答案】9
12.【答案】﹣ <﹣ < <π
13.【答案】9
14.【答案】9≤a<12
15.【答案】或
16.【答案】3或4;6n-3
17.【答案】解:原式 .
18.【答案】40°
19.【答案】;不等式组的所有整数解是:,0,1
20.【答案】证明:CD平分∠ACB,
∴∠ACD=∠DCB,
∵DE//AC,EF//CD,
∴∠ACD=∠EDC,∠FED=∠EDC,∠BEF=∠DCB
∴∠ACD=∠FED=∠DCB=∠BEF,
∴EF平分∠DEB.
21.【答案】(1)<;>
(2)①或;②
22.【答案】解:.理由如下:
延长交于点,
因为,
所以,
所以,
又,
所以,
所以,
所以.
.
23.【答案】(1)①,;②0≤t≤2或4≤t≤6;
(2)3
同课章节目录
