【高中数学北师大版(2019)同步练习】 4对数函数增长的比较(含答案)
文档属性
| 名称 | 【高中数学北师大版(2019)同步练习】 4对数函数增长的比较(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 09:24:55 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【高中数学北师大版(2019)同步练习】
4对数函数增长的比较
一、单选题
1.某地区植被被破坏,土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,则沙漠增加数y(万公顷)关于年数x的函数关系较为近似的是( )
A.y=0.2x B. C. D.y=0.2+log16x
2.已知某炮弹飞行高度h(单位:m)与时间x(单位:s)之间的函数关系式为 ,则炮弹飞行高度高于 的时间长为( )
A. B. C. D.
3.为落实党的二十大提出的“加快建设农业强国,扎实推动乡村振兴”的目标,银行拟在乡村开展小额贷款业务.根据调查的数据,建立了实际还款比例关于贷款人的年收入(单位:万元)的Logistic,模型:,已知当贷款人的年收入为8万元时,其实际还款比例为50%.若银行希望实际还款比例为40%,则贷款人的年收入为( )(精确到0.01万元,参考数据:,)
A.4.65万元 B.5.63万元 C.6.40万元 D.10.00万元
4.流行病学基本参数:基本再生数 指一个感染者传染的平均人数,世代间隔T指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可用模型: (其中 是开始确诊病例数)描述累计感染病例 随时间t(单位:天)的变化规律,指数增长率r与 ,T满足 ,有学者估计出 .据此,在新冠肺炎疫情初始阶段,当 时,t的值为( )( )
A.1.2 B.1.7 C.2.0 D.2.5
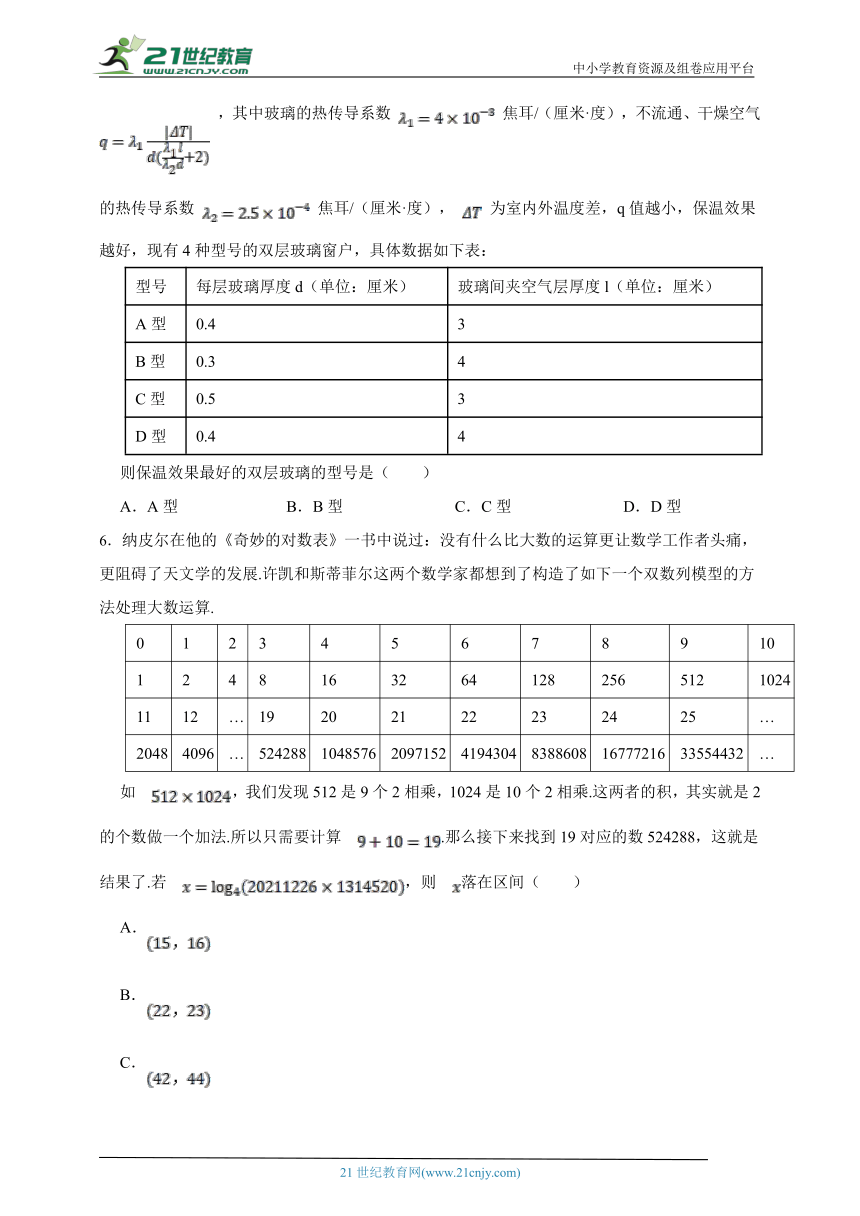
5.某学校数学建模小组为了研究双层玻璃窗户中每层玻璃厚度d(每层玻璃的厚度相同)及两层玻璃间夹空气层厚度l对保温效果的影响,利用热传导定律得到热传导量q满足关系式 ,其中玻璃的热传导系数 焦耳/(厘米·度),不流通、干燥空气的热传导系数 焦耳/(厘米·度), 为室内外温度差,q值越小,保温效果越好,现有4种型号的双层玻璃窗户,具体数据如下表:
型号 每层玻璃厚度d(单位:厘米) 玻璃间夹空气层厚度l(单位:厘米)
A型 0.4 3
B型 0.3 4
C型 0.5 3
D型 0.4 4
则保温效果最好的双层玻璃的型号是( )
A.A型 B.B型 C.C型 D.D型
6.纳皮尔在他的《奇妙的对数表》一书中说过:没有什么比大数的运算更让数学工作者头痛,更阻碍了天文学的发展.许凯和斯蒂菲尔这两个数学家都想到了构造了如下一个双数列模型的方法处理大数运算.
0 1 2 3 4 5 6 7 8 9 10
1 2 4 8 16 32 64 128 256 512 1024
11 12 … 19 20 21 22 23 24 25 …
2048 4096 … 524288 1048576 2097152 4194304 8388608 16777216 33554432 …
如 ,我们发现512是9个2相乘,1024是10个2相乘.这两者的积,其实就是2的个数做一个加法.所以只需要计算 .那么接下来找到19对应的数524288,这就是结果了.若 ,则 落在区间( )
A.
B.
C.
D.
二、多选题
7.某医药研究机构开发了一种新药,据监测,如果患者每次按规定的剂量注射该药物,注射后每毫升血液中的含药量y(微克)与时间t(小时)之间的关系近似满足如图所示的曲线.据进一步测定,当每毫升血液中含药量不少于0.125微克时,治疗该病有效,则( )
A.
B.注射一次治疗该病的有效时间长度为6小时
C.注射该药物 小时后每毫升血液中的含药量为0.4微克
D.注射一次治疗该病的有效时间长度为 时
8.一家货物公司计划租地建造仓库储存货物,经市场调查了解到下列信息:每月土地占地费 (单位:万元)与仓库到车站的距离x(单位:km)成反比,每月库存货物费 (单位:万元)与x成正比,若在距离车站10km处建仓库,则 为1万元, 为4万元,下列结论正确的是( )
A. B.
C. 有最小值4 D. 无最小值
三、填空题
9.物体在常温下的温度变化可以用牛顿冷却规律来描述:设物体的初始温度是,经过一定时间t(单位:min)后的温度是T,则,其中称为环境温度,h为常数,现有一杯用85℃热水冲的速溶咖啡,放在21℃的房间中,如果咖啡降到37℃需要16min,那么这杯咖啡要从37℃降到25℃,还需要 min.
10.某城市出租车按如下方法收费:起步价8元,可行3km(含3km),3km到10km(含10km)每走1km加价1.5元,10km后每走1km加价0.8元,某人坐该城市的出租车走了20km,他应交费 元.
11.按照国家的相关税法规定,作者的稿酬应该缴纳个人所得税,具体规定为:个人每次取得的稿酬收入,定额或定率减去规定费用后的余额为应纳税所得额,每次收入不超过4000元,首先减去每次稿酬所得费用800元;每次收入在4000元以上的,首先减除20%的费用并且以上两种情况均使用20%的比例税率,且按规定应纳税额征30%,已知某人出版一份书稿,共纳税280元,这个人应得稿费(扣税前)为 .
12.长江流域水库群的修建和联合调度,极大地降低了洪涝灾害风险,发挥了重要的防洪减灾效益.每年洪水来临之际,为保证防洪需要、降低防洪风险,水利部门需要在原有蓄水量的基础上联合调度,统一蓄水,用蓄满指数(蓄满指数=(水库实际蓄水量)÷(水库总蓄水量)×100)来衡量每座水库的水位情况.假设某次联合调度要求如下:
(ⅰ)调度后每座水库的蓄满指数仍属于区间 ;
(ⅱ)调度后每座水库的蓄满指数都不能降低;
(ⅲ)调度前后,各水库之间的蓄满指数排名不变.
记x为调度前某水库的蓄满指数,y为调度后该水库的蓄满指数,给出下面四个y关于x的函数解析式:
① ;② ;③ ;④ .
则满足此次联合调度要求的函数解析式的序号是 .
13.铅酸电池是一种蓄电池,电极主要由铅及其氧化物制成,电解液是硫酸溶液.这种电池具有电压稳定、价格便宜等优点,在交通、通信、电力、军事、航海、航空等领域有着广泛应用.但是由于在实际生活中使用方法不当,电池能量未被完全使用导致了能源的浪费,因此准确预测铅酸电池剩余放电时间是使用中急需解决的问题.
研究发现当电池以某恒定电流放电时,电压U关于放电时间1的变化率y满足y=aebt+ (其中a,b为常数,无理数e=2.71828……),实验数据显示当时间t的值为0和5时,电压U,关于放电时间t的变化率y分别为-2和-752,则a= ,b= (保留小数点后三位).
14.某公司决定采用增加广告投入和技术改造投入两项措施来获得更大的收益.通过市场的预测发现,当对两项投入都不大于3百万元时,每投入x百万元广告费,增加的销售额可近似的用函数 (百万元)来计算;每投入x百万元技术改造费用,增加的销售额可近似的用函数 (百万元)来计算.如果现在该公司共投入3百万元,分别用于广告投入和技术改造投入,那么预测该公司可增加的最大收益为 百万元.(注:收益=销售额﹣投入)
四、解答题
15.如图,某动物园要建造两间一样大小的长方形动物居室,可供建造围墙的材料总长为60m,设每间动物居室的宽为 m,面积为 m2
(1)若 ,求每间动物居室的面积 的值;
(2)求 关于 的函数关系式,并求函数的定义域;
(3)当动物居室的宽为多少时,才能使所建的每间动物居室面积最大,并求最大面积.
16.如图所示,设矩形 的周长为 ,把 沿 向 折叠, 折过去后交 于点 ,设 , .
(1)建立变量 与 之间的函数关系式 ,并写出函数 的定义域;
(2)求 的最大面积以及此时的 的值.
17.做一个体积为27 ,高为3m的长方形纸盒,当底面的边长取什么值时,用纸最少?最少用纸是多少?
18.某地打算修建一条公路,但设计路线正好经过一个野生动物迁徙路线,为了保护野生动物,决定修建高架桥,为野生动物的迁徙提供安全通道.若高架桥的两端及两端的桥墩已建好,两端的桥墩相距1200米,余下的工程只需要建两端桥墩之间的桥面和桥墩.经预测,一个桥墩的工程费用为500万元,距离为x米的相邻两桥墩之间的桥面工程费用为 万元,假设桥墩等距离分布,所有桥墩都视为点,且不考虑其它因素,记余下工程的费用为y万元.
(1)试写出y关于x的函数关系式;
(2)需新建多少个桥墩才能使y最小?并求出其最小值.参考数据: ,
19.某企业生产一种产品,根据经验,其次品率 与日产量 (万件)之间满足关系, (其中 为常数,且 ,已知每生产1万件合格的产品以盈利2万元,但每生产1万件次品将亏损1万元(注:次品率=次品数/生产量, 如 表示每生产10件产品,有1件次品,其余为合格品).
(1)试将生产这种产品每天的盈利额 (万元)表示为日产量 (万件)的函数;
(2)当日产量为多少时,可获得最大利润
20.设矩形 的周长为 ,把 沿 向 折叠, 折过去后交 于点 ,设 ,求 的最大面积及相应 的值.
答案解析部分
1.【答案】C
【知识点】根据实际问题选择函数类型
2.【答案】A
【知识点】函数模型的选择与应用
3.【答案】A
【知识点】一次函数、指数函数、对数函数的增长差异
4.【答案】B
【知识点】函数模型的选择与应用
5.【答案】D
【知识点】函数模型的选择与应用
6.【答案】B
【知识点】函数模型的选择与应用
7.【答案】A,D
【知识点】根据实际问题选择函数类型
8.【答案】B,C,D
【知识点】函数的最大(小)值;函数模型的选择与应用
9.【答案】16
【知识点】函数模型的选择与应用
10.【答案】26.5
【知识点】根据实际问题选择函数类型
11.【答案】2800
【知识点】函数模型的选择与应用
12.【答案】②④
【知识点】根据实际问题选择函数类型
13.【答案】;1.141
【知识点】有理数指数幂的运算性质;函数模型的选择与应用
14.【答案】
【知识点】函数模型的选择与应用
15.【答案】(1)解:当 时,每间动物居室的长为 ,
故 .
(2)解:由题意得,每间居室的长为 ,则 ,
由 得 ,故函数的定义域为 .
(3)解: ,
当 时, 有最大值,且最大值为75.
故当动物居室的宽为 时,所建的每间动物居室面积最大,且最大面积为 .
【知识点】根据实际问题选择函数类型
16.【答案】(1)依题意有: ,
折叠之后, , , ,
,则 , ,
又 , ,
在 中,有 ,化简得: ,即 .
即 ,解得 ,所以函数 的定义域为: .
(2)依题意有:
,
由基本不等式可得: ,当且仅当 即 时取等号,
于是 ,
综上: 的最大面积为 ,此时 .
【知识点】函数的最大(小)值;基本不等式在最值问题中的应用;函数模型的选择与应用
17.【答案】解:一个体积为27 ,高为3m,则底面面积为 ,
设长方体的底面边长为 ,则底面宽为 ,
所以长方体表面积
,
当且仅当 时,取等号,
所以当底面的边长取 时,用纸最少,最少用纸是 .
【知识点】根据实际问题选择函数类型
18.【答案】(1)解:由已知两端的桥墩相距1200米,且相邻两桥墩相距x米,故需要建桥墩 个,
则
所以y关于x的函数关系式为 ,
(2)解:由(1)知
令 ,即 ,解得 (舍)或
当 时, ,函数单调递减;当 时, ,函数单调递增;
所以当 时,y有最小值,
且
又
(万元)
所以需新建19个桥墩才能使y最小,最小值为24740万元.
【知识点】函数的最大(小)值;函数模型的选择与应用
19.【答案】(1)解:当 时, ,
∴ .
当 时, ,
∴ .
综上,日盈利额 (万元)与日产量x(万件)的函数关系式为
,(其中a为常数,且 ).
(2)解:当 时, ,其最大值为55万元.
当 时, ,设 ,则 ,
此时, ,
显然,当且仅当 ,即 时, 有最大值,为13.5万元.
令 ,得 ,
解得 (舍去)或 ,
则(i)当 时,日产量为11万件时,可获得最大利润5.5万元.
(ii)当 时, 时,
函数 可看成是由函数 与 复合而成的.
因为 ,所以 ,故 在 上为减函数
又 在 上为减函数,所以 在 上为增函数
故当日产量为a万件时,可获得最大利润 万元.
(iii)当 时,日产量为9万件时,可获得最大利润13.5万元.
【知识点】复合函数的单调性;基本不等式在最值问题中的应用;函数模型的选择与应用
20.【答案】解:如图,
设 ,由矩形 的周长为 ,可知 .设 ,则 ,
, , , ,
.
在 中,由勾股定理得 ,即 ,
解得 ,所以 .
所以 的面积为
.
由基本不等式与不等式的性质,得 ,
当且仅当 时,即当 时, 的面积最大,面积的最大值为
【知识点】基本不等式在最值问题中的应用;函数模型的选择与应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【高中数学北师大版(2019)同步练习】
4对数函数增长的比较
一、单选题
1.某地区植被被破坏,土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,则沙漠增加数y(万公顷)关于年数x的函数关系较为近似的是( )
A.y=0.2x B. C. D.y=0.2+log16x
2.已知某炮弹飞行高度h(单位:m)与时间x(单位:s)之间的函数关系式为 ,则炮弹飞行高度高于 的时间长为( )
A. B. C. D.
3.为落实党的二十大提出的“加快建设农业强国,扎实推动乡村振兴”的目标,银行拟在乡村开展小额贷款业务.根据调查的数据,建立了实际还款比例关于贷款人的年收入(单位:万元)的Logistic,模型:,已知当贷款人的年收入为8万元时,其实际还款比例为50%.若银行希望实际还款比例为40%,则贷款人的年收入为( )(精确到0.01万元,参考数据:,)
A.4.65万元 B.5.63万元 C.6.40万元 D.10.00万元
4.流行病学基本参数:基本再生数 指一个感染者传染的平均人数,世代间隔T指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可用模型: (其中 是开始确诊病例数)描述累计感染病例 随时间t(单位:天)的变化规律,指数增长率r与 ,T满足 ,有学者估计出 .据此,在新冠肺炎疫情初始阶段,当 时,t的值为( )( )
A.1.2 B.1.7 C.2.0 D.2.5
5.某学校数学建模小组为了研究双层玻璃窗户中每层玻璃厚度d(每层玻璃的厚度相同)及两层玻璃间夹空气层厚度l对保温效果的影响,利用热传导定律得到热传导量q满足关系式 ,其中玻璃的热传导系数 焦耳/(厘米·度),不流通、干燥空气的热传导系数 焦耳/(厘米·度), 为室内外温度差,q值越小,保温效果越好,现有4种型号的双层玻璃窗户,具体数据如下表:
型号 每层玻璃厚度d(单位:厘米) 玻璃间夹空气层厚度l(单位:厘米)
A型 0.4 3
B型 0.3 4
C型 0.5 3
D型 0.4 4
则保温效果最好的双层玻璃的型号是( )
A.A型 B.B型 C.C型 D.D型
6.纳皮尔在他的《奇妙的对数表》一书中说过:没有什么比大数的运算更让数学工作者头痛,更阻碍了天文学的发展.许凯和斯蒂菲尔这两个数学家都想到了构造了如下一个双数列模型的方法处理大数运算.
0 1 2 3 4 5 6 7 8 9 10
1 2 4 8 16 32 64 128 256 512 1024
11 12 … 19 20 21 22 23 24 25 …
2048 4096 … 524288 1048576 2097152 4194304 8388608 16777216 33554432 …
如 ,我们发现512是9个2相乘,1024是10个2相乘.这两者的积,其实就是2的个数做一个加法.所以只需要计算 .那么接下来找到19对应的数524288,这就是结果了.若 ,则 落在区间( )
A.
B.
C.
D.
二、多选题
7.某医药研究机构开发了一种新药,据监测,如果患者每次按规定的剂量注射该药物,注射后每毫升血液中的含药量y(微克)与时间t(小时)之间的关系近似满足如图所示的曲线.据进一步测定,当每毫升血液中含药量不少于0.125微克时,治疗该病有效,则( )
A.
B.注射一次治疗该病的有效时间长度为6小时
C.注射该药物 小时后每毫升血液中的含药量为0.4微克
D.注射一次治疗该病的有效时间长度为 时
8.一家货物公司计划租地建造仓库储存货物,经市场调查了解到下列信息:每月土地占地费 (单位:万元)与仓库到车站的距离x(单位:km)成反比,每月库存货物费 (单位:万元)与x成正比,若在距离车站10km处建仓库,则 为1万元, 为4万元,下列结论正确的是( )
A. B.
C. 有最小值4 D. 无最小值
三、填空题
9.物体在常温下的温度变化可以用牛顿冷却规律来描述:设物体的初始温度是,经过一定时间t(单位:min)后的温度是T,则,其中称为环境温度,h为常数,现有一杯用85℃热水冲的速溶咖啡,放在21℃的房间中,如果咖啡降到37℃需要16min,那么这杯咖啡要从37℃降到25℃,还需要 min.
10.某城市出租车按如下方法收费:起步价8元,可行3km(含3km),3km到10km(含10km)每走1km加价1.5元,10km后每走1km加价0.8元,某人坐该城市的出租车走了20km,他应交费 元.
11.按照国家的相关税法规定,作者的稿酬应该缴纳个人所得税,具体规定为:个人每次取得的稿酬收入,定额或定率减去规定费用后的余额为应纳税所得额,每次收入不超过4000元,首先减去每次稿酬所得费用800元;每次收入在4000元以上的,首先减除20%的费用并且以上两种情况均使用20%的比例税率,且按规定应纳税额征30%,已知某人出版一份书稿,共纳税280元,这个人应得稿费(扣税前)为 .
12.长江流域水库群的修建和联合调度,极大地降低了洪涝灾害风险,发挥了重要的防洪减灾效益.每年洪水来临之际,为保证防洪需要、降低防洪风险,水利部门需要在原有蓄水量的基础上联合调度,统一蓄水,用蓄满指数(蓄满指数=(水库实际蓄水量)÷(水库总蓄水量)×100)来衡量每座水库的水位情况.假设某次联合调度要求如下:
(ⅰ)调度后每座水库的蓄满指数仍属于区间 ;
(ⅱ)调度后每座水库的蓄满指数都不能降低;
(ⅲ)调度前后,各水库之间的蓄满指数排名不变.
记x为调度前某水库的蓄满指数,y为调度后该水库的蓄满指数,给出下面四个y关于x的函数解析式:
① ;② ;③ ;④ .
则满足此次联合调度要求的函数解析式的序号是 .
13.铅酸电池是一种蓄电池,电极主要由铅及其氧化物制成,电解液是硫酸溶液.这种电池具有电压稳定、价格便宜等优点,在交通、通信、电力、军事、航海、航空等领域有着广泛应用.但是由于在实际生活中使用方法不当,电池能量未被完全使用导致了能源的浪费,因此准确预测铅酸电池剩余放电时间是使用中急需解决的问题.
研究发现当电池以某恒定电流放电时,电压U关于放电时间1的变化率y满足y=aebt+ (其中a,b为常数,无理数e=2.71828……),实验数据显示当时间t的值为0和5时,电压U,关于放电时间t的变化率y分别为-2和-752,则a= ,b= (保留小数点后三位).
14.某公司决定采用增加广告投入和技术改造投入两项措施来获得更大的收益.通过市场的预测发现,当对两项投入都不大于3百万元时,每投入x百万元广告费,增加的销售额可近似的用函数 (百万元)来计算;每投入x百万元技术改造费用,增加的销售额可近似的用函数 (百万元)来计算.如果现在该公司共投入3百万元,分别用于广告投入和技术改造投入,那么预测该公司可增加的最大收益为 百万元.(注:收益=销售额﹣投入)
四、解答题
15.如图,某动物园要建造两间一样大小的长方形动物居室,可供建造围墙的材料总长为60m,设每间动物居室的宽为 m,面积为 m2
(1)若 ,求每间动物居室的面积 的值;
(2)求 关于 的函数关系式,并求函数的定义域;
(3)当动物居室的宽为多少时,才能使所建的每间动物居室面积最大,并求最大面积.
16.如图所示,设矩形 的周长为 ,把 沿 向 折叠, 折过去后交 于点 ,设 , .
(1)建立变量 与 之间的函数关系式 ,并写出函数 的定义域;
(2)求 的最大面积以及此时的 的值.
17.做一个体积为27 ,高为3m的长方形纸盒,当底面的边长取什么值时,用纸最少?最少用纸是多少?
18.某地打算修建一条公路,但设计路线正好经过一个野生动物迁徙路线,为了保护野生动物,决定修建高架桥,为野生动物的迁徙提供安全通道.若高架桥的两端及两端的桥墩已建好,两端的桥墩相距1200米,余下的工程只需要建两端桥墩之间的桥面和桥墩.经预测,一个桥墩的工程费用为500万元,距离为x米的相邻两桥墩之间的桥面工程费用为 万元,假设桥墩等距离分布,所有桥墩都视为点,且不考虑其它因素,记余下工程的费用为y万元.
(1)试写出y关于x的函数关系式;
(2)需新建多少个桥墩才能使y最小?并求出其最小值.参考数据: ,
19.某企业生产一种产品,根据经验,其次品率 与日产量 (万件)之间满足关系, (其中 为常数,且 ,已知每生产1万件合格的产品以盈利2万元,但每生产1万件次品将亏损1万元(注:次品率=次品数/生产量, 如 表示每生产10件产品,有1件次品,其余为合格品).
(1)试将生产这种产品每天的盈利额 (万元)表示为日产量 (万件)的函数;
(2)当日产量为多少时,可获得最大利润
20.设矩形 的周长为 ,把 沿 向 折叠, 折过去后交 于点 ,设 ,求 的最大面积及相应 的值.
答案解析部分
1.【答案】C
【知识点】根据实际问题选择函数类型
2.【答案】A
【知识点】函数模型的选择与应用
3.【答案】A
【知识点】一次函数、指数函数、对数函数的增长差异
4.【答案】B
【知识点】函数模型的选择与应用
5.【答案】D
【知识点】函数模型的选择与应用
6.【答案】B
【知识点】函数模型的选择与应用
7.【答案】A,D
【知识点】根据实际问题选择函数类型
8.【答案】B,C,D
【知识点】函数的最大(小)值;函数模型的选择与应用
9.【答案】16
【知识点】函数模型的选择与应用
10.【答案】26.5
【知识点】根据实际问题选择函数类型
11.【答案】2800
【知识点】函数模型的选择与应用
12.【答案】②④
【知识点】根据实际问题选择函数类型
13.【答案】;1.141
【知识点】有理数指数幂的运算性质;函数模型的选择与应用
14.【答案】
【知识点】函数模型的选择与应用
15.【答案】(1)解:当 时,每间动物居室的长为 ,
故 .
(2)解:由题意得,每间居室的长为 ,则 ,
由 得 ,故函数的定义域为 .
(3)解: ,
当 时, 有最大值,且最大值为75.
故当动物居室的宽为 时,所建的每间动物居室面积最大,且最大面积为 .
【知识点】根据实际问题选择函数类型
16.【答案】(1)依题意有: ,
折叠之后, , , ,
,则 , ,
又 , ,
在 中,有 ,化简得: ,即 .
即 ,解得 ,所以函数 的定义域为: .
(2)依题意有:
,
由基本不等式可得: ,当且仅当 即 时取等号,
于是 ,
综上: 的最大面积为 ,此时 .
【知识点】函数的最大(小)值;基本不等式在最值问题中的应用;函数模型的选择与应用
17.【答案】解:一个体积为27 ,高为3m,则底面面积为 ,
设长方体的底面边长为 ,则底面宽为 ,
所以长方体表面积
,
当且仅当 时,取等号,
所以当底面的边长取 时,用纸最少,最少用纸是 .
【知识点】根据实际问题选择函数类型
18.【答案】(1)解:由已知两端的桥墩相距1200米,且相邻两桥墩相距x米,故需要建桥墩 个,
则
所以y关于x的函数关系式为 ,
(2)解:由(1)知
令 ,即 ,解得 (舍)或
当 时, ,函数单调递减;当 时, ,函数单调递增;
所以当 时,y有最小值,
且
又
(万元)
所以需新建19个桥墩才能使y最小,最小值为24740万元.
【知识点】函数的最大(小)值;函数模型的选择与应用
19.【答案】(1)解:当 时, ,
∴ .
当 时, ,
∴ .
综上,日盈利额 (万元)与日产量x(万件)的函数关系式为
,(其中a为常数,且 ).
(2)解:当 时, ,其最大值为55万元.
当 时, ,设 ,则 ,
此时, ,
显然,当且仅当 ,即 时, 有最大值,为13.5万元.
令 ,得 ,
解得 (舍去)或 ,
则(i)当 时,日产量为11万件时,可获得最大利润5.5万元.
(ii)当 时, 时,
函数 可看成是由函数 与 复合而成的.
因为 ,所以 ,故 在 上为减函数
又 在 上为减函数,所以 在 上为增函数
故当日产量为a万件时,可获得最大利润 万元.
(iii)当 时,日产量为9万件时,可获得最大利润13.5万元.
【知识点】复合函数的单调性;基本不等式在最值问题中的应用;函数模型的选择与应用
20.【答案】解:如图,
设 ,由矩形 的周长为 ,可知 .设 ,则 ,
, , , ,
.
在 中,由勾股定理得 ,即 ,
解得 ,所以 .
所以 的面积为
.
由基本不等式与不等式的性质,得 ,
当且仅当 时,即当 时, 的面积最大,面积的最大值为
【知识点】基本不等式在最值问题中的应用;函数模型的选择与应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
