湖北省襄阳市2023-2024学年高一下学期期末教学质量统一检测数学试题(无答案)
文档属性
| 名称 | 湖北省襄阳市2023-2024学年高一下学期期末教学质量统一检测数学试题(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 453.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-30 00:00:00 | ||
图片预览


文档简介
湖北省襄阳市22023-2024学年高一下学期期末教学质量统一检测数学试题
一、选择题:本题共 8 小题, 每小题 5 分, 共 40 分. 在每小题给出的四个选项中, 只有一项是符合题目要求的.
1. 已知,则( )
A. B. C. D.
2. 已知向量,不共线,且向量与共线,则实数的值为( )
A. -2或-1 B. -2或1 C. -1或2 D. 1或2
3. 利用简单随机抽样,从个个体中抽取一个容量为10的样本.若抽完第一个个体后,余下的每个个体被抽到的机会为,则在整个抽样过程中,每个个体被抽到的机会为( )
A. B. C. D.
4. 《九章算术》问题十:今有方亭,下方五丈,上方四丈.高五丈.问积几何(今译:已知正四棱台体建筑物(方亭)如图,下底边长丈,上底边长丈.高丈.问它的体积是多少立方丈?( )
A. B. C. D.
5. 甲在微信群中发布6元“拼手气”红包一个,被乙、丙、丁三人抢完.若三人均领到整数元,且每人至少领到1元,则乙获得“最佳手气”(即乙领取的钱数不少于其他任何人)的概率是( )
A. B. C. D.
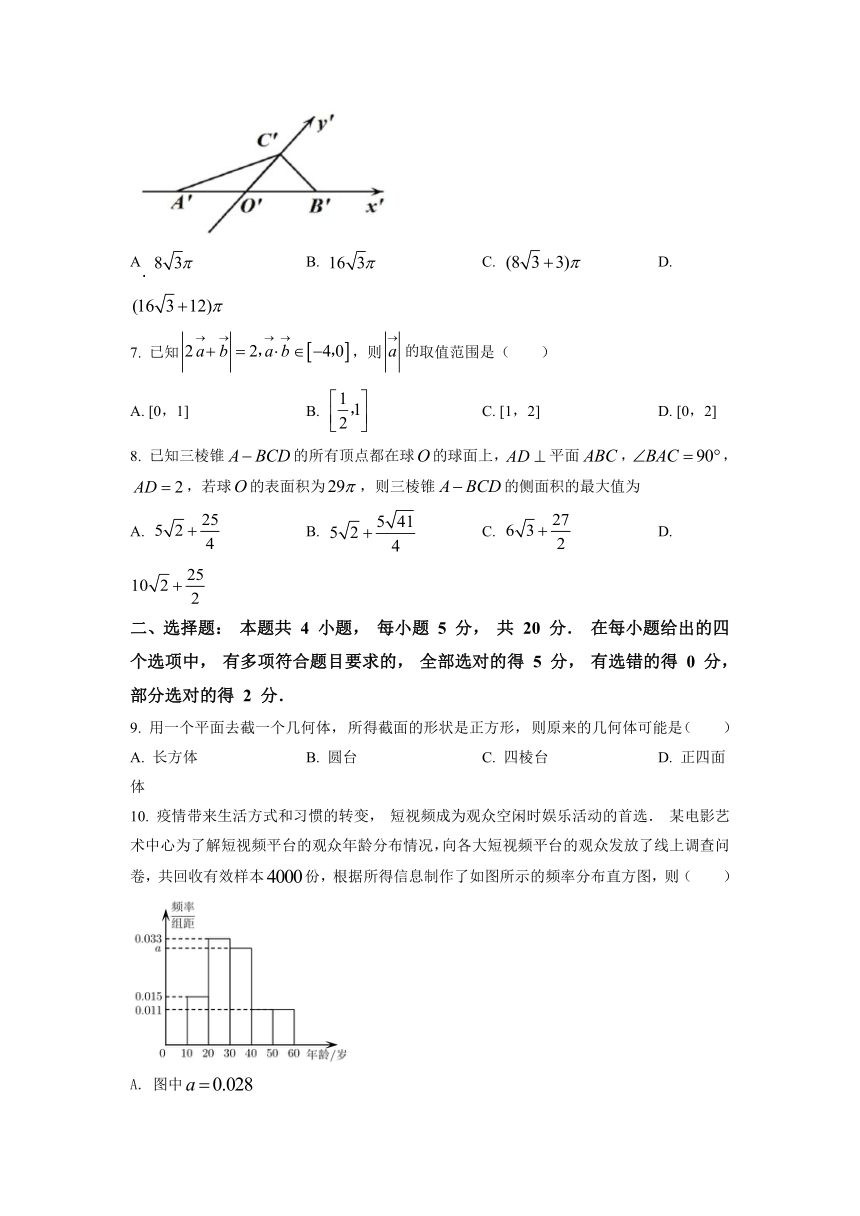
6. 水平放置的,用斜二测画法作出的直观图是如图所示的,其中 ,则绕AB所在直线旋转一周后形成的几何体的表面积为( )
A B. C. D.
7. 已知,则取值范围是( )
A. [0,1] B. C. [1,2] D. [0,2]
8. 已知三棱锥的所有顶点都在球的球面上,平面,,,若球的表面积为,则三棱锥的侧面积的最大值为
A. B. C. D.
二、选择题: 本题共 4 小题, 每小题 5 分, 共 20 分. 在每小题给出的四个选项中, 有多项符合题目要求的, 全部选对的得 5 分, 有选错的得 0 分, 部分选对的得 2 分.
9. 用一个平面去截一个几何体, 所得截面的形状是正方形, 则原来的几何体可能是( )
A. 长方体 B. 圆台 C. 四棱台 D. 正四面体
10. 疫情带来生活方式和习惯的转变, 短视频成为观众空闲时娱乐活动的首选. 某电影艺术中心为了解短视频平台的观众年龄分布情况,向各大短视频平台的观众发放了线上调查问卷,共回收有效样本份,根据所得信息制作了如图所示的频率分布直方图,则( )
A. 图中
B. 在份有效样本中, 短视频观众年龄在岁的有人
C. 估计短视频观众的平均年龄为岁
D. 估计短视频观众年龄的分位数为岁
11. 已知是等腰直角三角形, , 用斜二测画法画出它的直观图 , 则的长可能是( )
A. B. C. D.
12. 如图, 已知均为等边三角形, 分别为中点,为内一点 (含边界). , 下列说法正确的是( )
A. 延长交于, 则
B. 若, 则为的重心
C. 若,则点的轨迹是一条线段
D. 最小值是
非选择题部分
三、填空题: 本题共 4 小题, 每小题 5 分, 共 20 分.
13. 直播带货已成为一种新的消费方式, 据某平台统计, 在直播带货销量中, 服装鞋帽类占, 食品饮料类占, 家居生活类占19%, 美妆护肤类占, 其他占.为了解直播带货各品类的质量情况,现按分层随机抽样的方法抽取一个容量为的样本.已知在抽取的样本中,服装鞋帽类有560件,则家居生活类有_____________件
14. 如图,在四面体中,,,、分别为、的中点,,则异面直线与所成的角是_____________.
15. 如图, 在Rt 中, 点是斜边的中点, 点在边上, 且, 则___________.
16. 已知,且,实数满足,且,则最小值是___________.
四、解答题: 本题共 6小题, 共 70 分, 解答应写出文字说明、证明过和或演算步骤.
17. 已知向量满足.
(1)若,求||的值;
(2)若,求的值.
18. 如图,已知在正三棱柱中,D为棱AC的中点,.
(1)求正三棱柱的表面积;
(2)求证:直线//平面.
19. 如图, 四棱锥的底面四边形为正方形, 顶点 在底面的射影为线段的中点 是的中点,
(1)求证:平面;
(2)求过点的平面截该棱锥得到两部分的体积之比.
20. 在①,②,③, 这三个条件中任选一个, 补充在下面问题中并求解. 问题: 如图, 在中, 角所对的边分别为是边上一点, , , 若_________,
(1)求角A的值;
(2)求的值.
21. 如图, 在正六边形中,,为上一点, 且 交于点
(1)当 时, 试用表示;
(2)求的取值范围.
22. 某校有高中生2000人,其中男女生比例约为,为了获得该校全体高中生的身高信息,采取了以下两种方案:方案一:采用比例分配的分层随机抽样方法,抽收了样本容量为的样本,得到频数分布表和频率分布直方图.方案二:采用分层随机抽样方法,抽取了男、女生样本量均为25的样本,计算得到男生样本的均值为170,方差为16,女生样本的均值为160,方差为20.
身高(单位:)
频数 6 4
(1)根据图表信息,求,并补充完整频率分布直方图,估计该校高中生的身高均值;(同一组中的数据以这组数据所在区间中点的值为代表)
(2)计算方案二中总样本的均值及方差;
(3)计算两种方案总样本均值的差,并说明用方案二总样本的均值作为总体均值的估计合适吗?为什么?
一、选择题:本题共 8 小题, 每小题 5 分, 共 40 分. 在每小题给出的四个选项中, 只有一项是符合题目要求的.
1. 已知,则( )
A. B. C. D.
2. 已知向量,不共线,且向量与共线,则实数的值为( )
A. -2或-1 B. -2或1 C. -1或2 D. 1或2
3. 利用简单随机抽样,从个个体中抽取一个容量为10的样本.若抽完第一个个体后,余下的每个个体被抽到的机会为,则在整个抽样过程中,每个个体被抽到的机会为( )
A. B. C. D.
4. 《九章算术》问题十:今有方亭,下方五丈,上方四丈.高五丈.问积几何(今译:已知正四棱台体建筑物(方亭)如图,下底边长丈,上底边长丈.高丈.问它的体积是多少立方丈?( )
A. B. C. D.
5. 甲在微信群中发布6元“拼手气”红包一个,被乙、丙、丁三人抢完.若三人均领到整数元,且每人至少领到1元,则乙获得“最佳手气”(即乙领取的钱数不少于其他任何人)的概率是( )
A. B. C. D.
6. 水平放置的,用斜二测画法作出的直观图是如图所示的,其中 ,则绕AB所在直线旋转一周后形成的几何体的表面积为( )
A B. C. D.
7. 已知,则取值范围是( )
A. [0,1] B. C. [1,2] D. [0,2]
8. 已知三棱锥的所有顶点都在球的球面上,平面,,,若球的表面积为,则三棱锥的侧面积的最大值为
A. B. C. D.
二、选择题: 本题共 4 小题, 每小题 5 分, 共 20 分. 在每小题给出的四个选项中, 有多项符合题目要求的, 全部选对的得 5 分, 有选错的得 0 分, 部分选对的得 2 分.
9. 用一个平面去截一个几何体, 所得截面的形状是正方形, 则原来的几何体可能是( )
A. 长方体 B. 圆台 C. 四棱台 D. 正四面体
10. 疫情带来生活方式和习惯的转变, 短视频成为观众空闲时娱乐活动的首选. 某电影艺术中心为了解短视频平台的观众年龄分布情况,向各大短视频平台的观众发放了线上调查问卷,共回收有效样本份,根据所得信息制作了如图所示的频率分布直方图,则( )
A. 图中
B. 在份有效样本中, 短视频观众年龄在岁的有人
C. 估计短视频观众的平均年龄为岁
D. 估计短视频观众年龄的分位数为岁
11. 已知是等腰直角三角形, , 用斜二测画法画出它的直观图 , 则的长可能是( )
A. B. C. D.
12. 如图, 已知均为等边三角形, 分别为中点,为内一点 (含边界). , 下列说法正确的是( )
A. 延长交于, 则
B. 若, 则为的重心
C. 若,则点的轨迹是一条线段
D. 最小值是
非选择题部分
三、填空题: 本题共 4 小题, 每小题 5 分, 共 20 分.
13. 直播带货已成为一种新的消费方式, 据某平台统计, 在直播带货销量中, 服装鞋帽类占, 食品饮料类占, 家居生活类占19%, 美妆护肤类占, 其他占.为了解直播带货各品类的质量情况,现按分层随机抽样的方法抽取一个容量为的样本.已知在抽取的样本中,服装鞋帽类有560件,则家居生活类有_____________件
14. 如图,在四面体中,,,、分别为、的中点,,则异面直线与所成的角是_____________.
15. 如图, 在Rt 中, 点是斜边的中点, 点在边上, 且, 则___________.
16. 已知,且,实数满足,且,则最小值是___________.
四、解答题: 本题共 6小题, 共 70 分, 解答应写出文字说明、证明过和或演算步骤.
17. 已知向量满足.
(1)若,求||的值;
(2)若,求的值.
18. 如图,已知在正三棱柱中,D为棱AC的中点,.
(1)求正三棱柱的表面积;
(2)求证:直线//平面.
19. 如图, 四棱锥的底面四边形为正方形, 顶点 在底面的射影为线段的中点 是的中点,
(1)求证:平面;
(2)求过点的平面截该棱锥得到两部分的体积之比.
20. 在①,②,③, 这三个条件中任选一个, 补充在下面问题中并求解. 问题: 如图, 在中, 角所对的边分别为是边上一点, , , 若_________,
(1)求角A的值;
(2)求的值.
21. 如图, 在正六边形中,,为上一点, 且 交于点
(1)当 时, 试用表示;
(2)求的取值范围.
22. 某校有高中生2000人,其中男女生比例约为,为了获得该校全体高中生的身高信息,采取了以下两种方案:方案一:采用比例分配的分层随机抽样方法,抽收了样本容量为的样本,得到频数分布表和频率分布直方图.方案二:采用分层随机抽样方法,抽取了男、女生样本量均为25的样本,计算得到男生样本的均值为170,方差为16,女生样本的均值为160,方差为20.
身高(单位:)
频数 6 4
(1)根据图表信息,求,并补充完整频率分布直方图,估计该校高中生的身高均值;(同一组中的数据以这组数据所在区间中点的值为代表)
(2)计算方案二中总样本的均值及方差;
(3)计算两种方案总样本均值的差,并说明用方案二总样本的均值作为总体均值的估计合适吗?为什么?
同课章节目录
