【新教材】人教A版(2019)高中数学选择性必修第一册《空间向量及其线性运算》课件(共71张PPT)
文档属性
| 名称 | 【新教材】人教A版(2019)高中数学选择性必修第一册《空间向量及其线性运算》课件(共71张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 00:00:00 | ||
图片预览







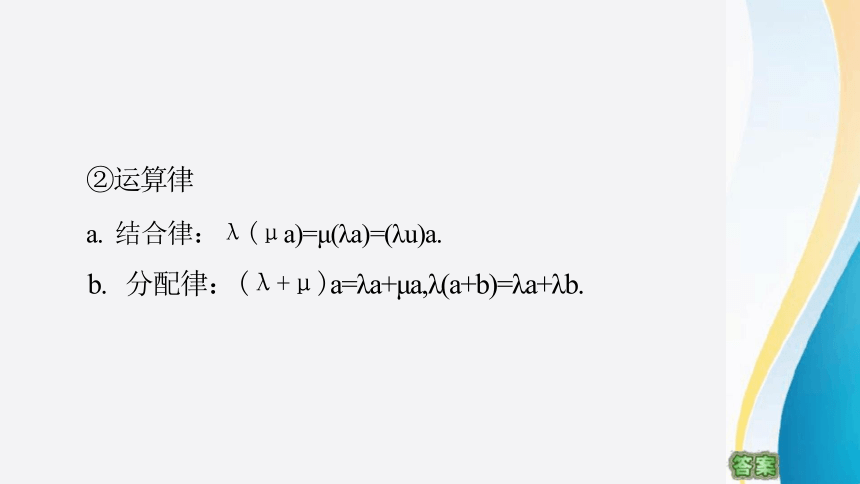


文档简介
(共71张PPT)
第一章空间向量与立体几何
1. 1 空间向量及其运算
1.1.1 空间向量及其线性运算
学 习 目 标
核 心 素 养
1.理解空间向量的概念.(难点) 2.掌握空间向量的线性运算.(重 点 ) 3.掌握共线向量定理、共面向量 定理及推论的应用.(重点、难 点 )
1.通过空间向量有关概念的学习,
培养学生的数学抽象核心素养.
2.借助向量的线性运算、共线向量
及共面向量的学习,提升学生的直
观想象和逻辑推理的核心素养.
.情景导学:探、新知
情境引入·助学助教
国庆期间,某游客从上海世博园(O)游览结束后乘车到外滩(A)观
赏黄浦江,然后抵达东方明珠(B)游玩,如图1,游客的实际位移是什
么 可以用什么数学概念来表示这个过程
如果游客还要登上东方明珠顶端(D)俯瞰上海美丽的夜景,如图
2,那么他实际发生的位移是什么 又如何表示呢
新知初探一
1.空间向量
(1)定义:在空间,具有大小和方向的量叫做空间向量.
(2)长度或模:空间向量的大小.
(3)表示方法:
①几何表示法:空间向量用有向线段表示;
②字母表示法:用字母a,b,c, … 表示;若向量a 的起点是A,
终点是B, 也可记作:AB, 其模记为la 或 B
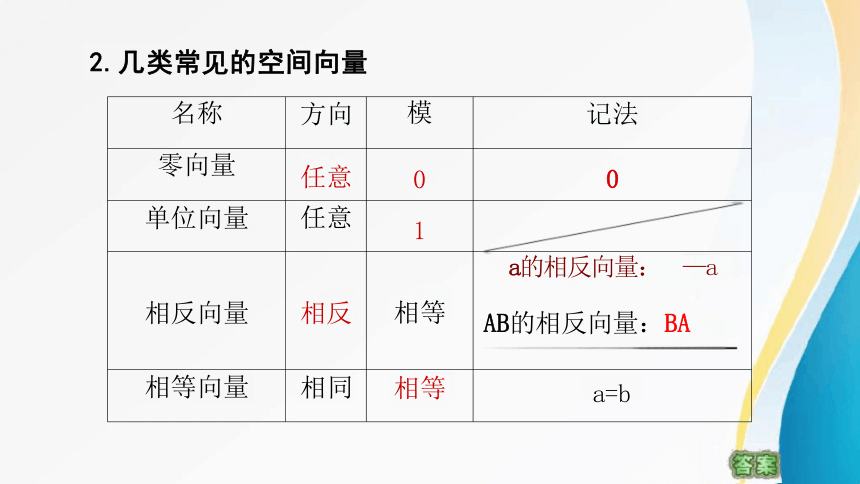
名称 方向 模
记法
零向量 任意 0
0
单位向量 任意 1
相反向量 相反 相等
a的相反向量: —a
AB的相反向量:BA
相等向量 相同 相等
a=b
2.几类常见的空间向量
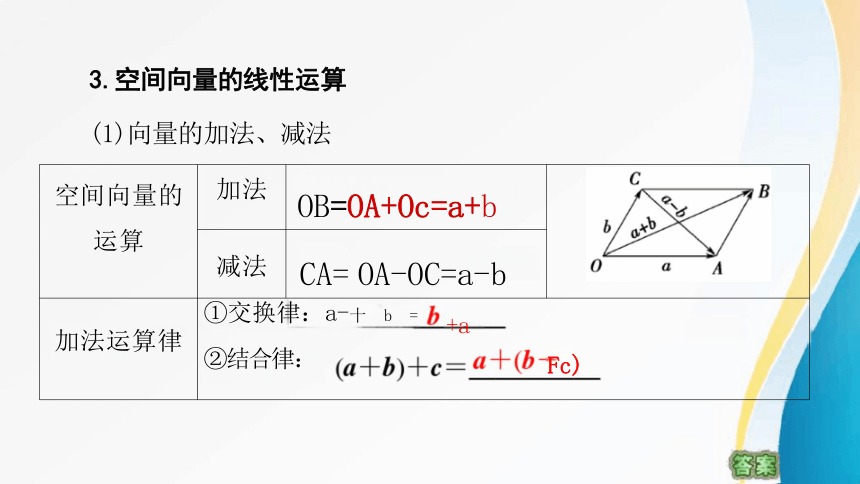
空间向量的 运算 加法 OB=OA+Oc=a+b
减法 CA= OA-OC=a-b
加法运算律 ①交换律:a-十 b = ②结合律: +a Fc)
3.空间向量的线性运算
(1)向量的加法、减法
(2)空间向量的数乘运算
①定义:实数λ与空间向量a 的乘积λa 仍然是一个向量,称为
向量的数乘运算.
当λ>0时, λa 与向量a 方向相同;
当λ<0时, λa 与向量a 方 向相反;
当λ=0时, λa= 0 ;λa 的长度是a 的长度的风 _倍.
②运算律
a. 结合律:λ(μa)=μ(λa)=(λu)a.
b. 分配律:(λ+μ)a=λa+μa,λ(a+b)=λa+λb.
思考:向量运算的结果与向量起点的选择有关系吗
提示没有关系.
4.共线向量
(1)定义:表示若干空间向量的有向线段所在的直线
互相平行或重合,则这些向量叫做共线向量或平行向量.
(2)方向向量:在直线1上取非零向量a, 与 向 量a 平行的非零向
量称为直线l 的方向向量.
规定:零向量与任意向量平行,即对任意向量a, 都有0//a.
(3)共线向量定理:对于空间任意两个向量a,b(b≠0),a// b 的
充要条件是存在实数λ使a=λb .
(4)如图,O 是直线l上一点,在直线l上取非零向量a, 则对于
直线l 上任意一点P, 由数乘向量定义及向量共线的充要条件可知,
存在实数入,使得OP=λa.
5.共面向量
(1)定义:平行于同一个平面的向量叫做共面向量.
(2)共面向量定理:若两个向量a,b 不共线,则向量p 与向量a,
b 共面的充要条件是存在唯一的有序实数对(x,y), 使p=xa+yb.
(3)空间一点P 位于平面ABC 内的充要条件:存在有序实数对(x,
y), 使AP= xAB+yAC 或对空间任意一 点0,有oP=OA+xAB+yAC
思 考:(1)空间中任意两个向量一定是共面向量吗
(2)若空间任意一点O 和不共线的三点A,B,C, 满足
则点P 与 点A,B,C 是否共面
为同一个平面的两个向量,因此一定是共面向量.
(2)由op=s0A+soB+sOC 得op-oA=(oB-oA
OA)
因此点P 与 点A,B,C 共面 .
[提示] (1)空间中任意两个向量都可以平移到同一个平面内,成
初试身手一
1. 思考辨析(正确的打“√ ”,错误的打“×”)
(1)空间向量a,b,c, 若 a//b,b //c,则a//c.
(2)相等向量一定是共线向量.
(3)三个空间向量一定是共面向量.
(4)零向量没有方向.
( )
( )
( )
( )
[提示] ( 1 ) × 若b=0 时 ,a 与 c 不一定平行.
(2) √ 相等向量一定共线,但共线不一定相等.
(3)×空间两个向量一定是共面向量,但三个空间向量可能是
共面的,也可以是不共面的.
(4)× 零向量有方向,它的方向是任意的.
2.如图所示,在四棱柱ABCD-A B C D 所有的棱中,可作为直
线A B 的方向向量的有( )
A.1 个 B.2 个 C.3 个 D.4
D [共四条AB,A B ,CD,C D .]
个
[因为 C 在线段AB 上,所以AB与BC方向相反,又因|AB
=5,|BC|=3,故
3 . 点C 在线段AB上,且AB|=5,|BC|=3,AB=λBC, 则λ=
0 [延长DE交边BC于
点F, 连接AF, 则有
BC=AF,
DF=AF, 故
DE-AD=0.]
4.在三棱锥A-BCD中,若△BCD
是正三角形,E 为其中心,则
化简的结果为 .
合.作.探究.释、疑:难
【例1】 (1)给出下列命题:
①若|a|=|b|,则 a=b 或a=—b;
②若向量a 是向量b 的相反向量,则|a|=|b;
③在正方体ABCD-A B C D 中 ,AC=A C1;
④若空间向量m, n,p 满足m=n , n=p, 则 m=p.
其中正确命题的序号是 .
类 型1 空间向量的有关概念
(2)如图所示,在平行六面体ABCD-A'B'C'D'中,顶点连接的向量
中,与向量AA'相等的向量有 ;与向量AB '相反的向量有
.(要求写出所有适合条件的向量)
(1)②③④ (2)BB',Cc,DD′BA',BA,CD,CD′ [(1)对于
①, 向 量a 与 b 的方向不一定相同或相反,故①错;
对于②,根据相反向量的定义知|a|=|b|,故②正确;
对于③,根据相等向量的定义知,AC=A C , 故③正确;
对于④,根据相等向量的定义知正确.
(2)根据相等向量的定义知,与向量AA'相等的向量有BB',CC
DD.与向量AB'相反的向量有BA',BA,CD,CD'.]
规律方法
解答空间向量有关概念问题的关键点及注意点
(1)关键点:紧紧抓住向量的两个要素,即大小和方向.
(2)注意点:注意一些特殊向量的特性.
①零向量不是没有方向,而是它的方向是任意的,且与任何向
量都共线,这一点说明了共线向量不具备传递性.
规律方法
②单位向量方向虽然不一定相同,但它们的长度都是1.
③两个向量模相等,不一定是相等向量;反之,若两个向量相
等,则它们不仅模相等,方向也相同.若两个向量模相等,方向相反,
则它们为相反向量.
[跟进训练]
1.下列关于空间向量的命题中,正确命题的个数是( )
①长度相等、方向相同的两个向量是相等向量;
②平行且模相等的两个向量是相等向量;
③若a≠b , 则| a|≠|b|;
④两个向量相等,则它们的起点与终点相同.
A.0 B.1 C.2 D.3
B [根据向量的定义,知长度相等、方向相同的两个向量是相等
向量,①正确;平行且模相等的两个向量可能是相等向量,也可能是
相反向量,②不正确;当a=—b 时,也有|a|=|b,③ 不正确;只要
模相等、方向相同,两个向量就是相等向量,与向量的起点与终点无 关,④不正确.综上可知只有①正确,故选B.]
式中运算结果为向量AC 的有( )
① B+BC
C ;
③(AB+BB )+B C ;
1B B C .
A.1 个 B.2 个 C.3 个 D.4 个
类 型2 空间向量的线性运算
【例 2】 (1)如图所示,在正方体 ABCD-A B C D 中,下列各
(2)已知正四棱锥P-ABCD,O 是正方形 ABCD 的中心,Q 是 CD
的中点,求下列各式中x,y,z 的值 .
①0Q=PQ+yPC+zPA;
②PA=xPO+yPQ+PD.
[思路探究] (1)合理根据向量的三角形和平行四边形法则,以及
在平行六面体中,体对角线向量等于从同一起点出发的三条棱向量的
和 . 如AC =AB+AD+AA1.
(2)根据数乘向量及三角形或平行四边形法则求解.
(1)D [对于①,(AB+BC)+Cc =AC+CC =AC ;
对 于 ② ,(AA +A D )+D C =AD +D C =AC ;
对 于 ③ ,(AB+BB )+B C =AB +B C =AC ;
对 于 ④ ,(AA +A B )+B C =AB +B C =AC .]
②∵ 0 为AC的中点,Q 为 CD的中点,
∴PA+PC=2PO,PC+PD=2PQ,
∴PA=2PO-PC,PC=2PQ-PD,
∴PA=2PO-2PQ+PD,∴x=2,y=-2.
规律方法
1.空间向量加法、减法运算的两个技巧
(1)巧用相反向量:向量减法的三角形法则是解决空间向量加法、
减法的关键,灵活运用相反向量可使向量首尾相接.
(2)巧用平移:利用三角形法则和平行四边形法则进行向量加、
减法运算时,务必注意和向量、差向量的方向,必要时可采用空间向
量的自由平移获得运算结果.
规律方法
2.利用数乘运算进行向量表示的技巧
(1)数形结合:利用数乘运算解题时,要结合具体图形,利用三
角形法则、平行四边形法则,将目标向量转化为已知向量.
(2)明确目标:在化简过程中要有目标意识,巧妙运用中点性质.
[跟进训练]
2.已知空间四边形ABCD, 连接AC,BD, 设 M,G 分别是BC,
CD的中点,则MG-AB+AD 等于( )
A. B.3MG C.3GM D.2MG
B [MG-AB+AD=MG-(AB-AD)=MG-DB
=MG+BD=MG+2MG=3MG.]
类型37 共线问题
【 例 3 】( 1 ) 设 e ,e 是空间两个不共线的向量,已知AB=e
+ke ,BC=5e +4e ,DCc=—e -2e , 且A,B,D 三点共线,实数
k= _.
(2)如图所示,已知四边形ABCD,ABEF 都是平行四边形且不共
面 ,M,N 分别是AC,BF 的中点,判断CE与MN是否共线.
思 论究 (1)根据向量共线的充要条件求解.
(2)根据数乘向量及三角形法则,把MN表示成λCE的形式,再根
据向量共线的充要条件求解.
(1)1 [AD=AB+BC+CD=(e +ke )+(5e +4e )+(e +2e )=
7e +(k+6)e .
设AD=λAB,则 7e +(k+6)e =λ(e +ke )
所 ,解得k=1.]
以上
两式相加得CE=2MN,
所以CE//MN, 即 CE 与MN 共线.
(2)[解] 法 一:因为 M,N 分别是 AC,BF 的中点,且四边形
ABCD,四边形ABEF都是平行四边形,所以
法二:因为四边形 ABEF 为平行四边形,所以连接 AE 时 ,AE
必过点N.
∴CE=AE-AC=2AN—2AM
=2(AN-AM)=2MN.
所以CE//MN, 即 CE 与MN 共线.
● 规 律 方 法
证明空间三点共线的三种思路
对于空间三点P,A,B 可通过证明下列结论来证明三点共线.
(1)存在实数λ,使A=λPB 成立.
(2)对空间任一点O, 有OP=OA+tAB(t∈ R).
(3)对空间任一点O, 有OP=xOA+yOB(x+y=1).
2ED ,F 在对角线A C上 ,
求 证 :E,F,B 三点共线.
3.如图,在正方体ABCD-A B C D 中 ,E 在A D 上,且 A E =
[跟进训练]
[证明] 设AB=a,AD=b,AA =c,
因为A E=2ED , 9
所 9 9
所 所以E,F,B 三点共线.
所以EF=
[探究问题]
1.什么样的向量算是共面向量
[提示] 能够平移到同一个平面内的向量称为共面向量.
类 型 4 向量共面问题
2 . 能说明P,A,B,C 四点共面的结论有哪些
[提示] ( 1)存在有序实数对(x,y), 使得AP=xAB
(2)空间一点P在平面ABC内的充要条件是存在有序实数组(x,
y,z) 使得OP=xOA+yOB+zOC (其中x+y+z=1).
(3)四点中任意两点的方向向量与另外两点的方向向量共线,如
PA//BC.
3 . 已知向量a,b,c 不共面,且p=3a+2b +c,m=a—b+c,
n=a+b—c, 试判断p,m,n 是否共面.
[提示] 设p=xm+yn, 即3a+2b+c=x(a-b+c)+
y(a+b—c)=(x+y)a+ (一x+y)b+(x—y)c.
因为a,b,c 不共面,所以
而此方程组无解,所以p不能用m,n 表示,
即p,m,n 不共面.
【例4】 已 知A,B,C 三点不共线,O 为平面ABC外一点,若
点M 满足
(1)判断MA,MB,M C三个向量是否共面;
(2)判断M 是否在平面ABC 内 .
元(1)根据向量共面的充要条件,即判断是否 MA =
xMB+yMC;(2) 根据(1)的结论,也可以利用OM=xOA+yOB+ zoC
中x+y+z 是否等于1.
[解] (1)∵OA+OB+0c=30M,
∴OA-OM=(OM-OB)+(OM-OC),
∴MA=BM+CM=—MB—MC,
∴向量MA,MB,MC 共面.
(2)由(1)知向量MA,MB,M C共面,而它们有共同的起点M , 且
A,B,C 三点不共线,∴M,A,B,C 共面,即M在平面ABC内 .
1. [变条件] 若把本例中条件
“OA+2OB=6OP-30C”, 点P 是否与点A 、B 、C 共面.
[解]∵3OP-30c=OA+2OB-3OP=(OA
2OP),
∴3CP=PA+2PB,即PA=-2PB-3PC.
根据共面向量定理的推论知:点P 与点A,B,C 共面.
[母题探究]
改为
OB—
2. [变条件] 若把本例条件变成“OP+0C=40A-OB”,
是否与点A 、B 、C 共面.
[解] 设OP=0A+xAB+yAC(x,y∈R), 则
OA+xAB+yAC+0c=40A-OB,
∴OA+x(OB-OA)+y(OC-OA)+0C=40A-OB,
∴(1-x-y-4)OA+(1+x)OB+(1+y)OC=0,
点 P
由题意知OA,OB,OC 均为非零向量,所以x,y 满足:
显然此方程组无解,故点P 与点A,B,C 不
共面.
3.[变解法] 上面两个母题探究,还可以用什么方法判断
[解] ( 1)由题意知,
, 点P与点A 、B 、C共面.
(2)∵OP=40A-OB-OC,而4-1-1=2≠1.
∴点P 与点A 、B 、C 不共面.
·
●规律方法
解决向量共面的策略
(1)若已知点P 在平面ABC内,则有AP=xAB+yAC 或OP=xOA+
yOB+zOC(x+y +z =1), 然后利用指定向量表示出已知向量,用待
定系数法求出参数.
(2)证明三个向量共面(或四点共面),需利用共面向量定理,证
明过程中要灵活进行向量的分解与合成,将其中一个向量用另外两 个向量来表示.
课堂小结. 提素· 养
必 备 素 养一
1.一些特殊向量的特性
(1)零向量不是没有方向,而是它的方向是任意的.
(2)单位向量方向虽然不一定相同,但它们的长度都是1.
(3)两个向量模相等,不一定是相等向量,反之,若两个向量相
等,则它们不仅模相等,方向也相同.若两个向量模相等,方向相
反,则它们为相反向量.
2.OP=OA+xAB+yAC 称为空间平面ABC的向量表达式.由此
可知空间中任意平面由空间一点及两个不共线向量唯一确定.
3.证明(或判断)A,B,C 三点共线时,只需证明存在实数λ,使
AB=λBC (或AB= λAC)即可,也可用“对空间任意一点O, 有 0c =
tOA+(1-t)OB” 来证明A,B,C 三点共线.
4. 空间一点P 位于平面MAB内的充要条件是存在有序实数对
(x,y), 使 MP=x MA +y MB, 满足这个关系式的点都在平面MAB
内;反之,平面MAB内的任一点都满足这个关系式.这个充要条件
常用于证明四点共面.
5.直线的方向向量是指与直线平行或共线的非零向量, 一条直
线的方向向量有无穷多个,它们的方向相同或相反.
6 . 向量p与向量a,b 共面的充要条件是在a 与b不共线的前提下
才成立的,若a 与b共线,则不成立.
MC=0 得MA=—MB—
MC ,故M,A,B,C 共
面 . ]
学以致用一
1.下列条件中使M与A,B,C
共面的是( )
A.OM=20A-OB-OC
C.MA+MB+MC=0
D.OM+OA+OB+OC=0
C [由MA+ MB +
一定
2. 已知正方体ABCD-A B C D , 若 点F 是侧面CD 的中心,且
AF=AD+mAB-nAA , 则m,n 的值分别为( )
A. ,-2 B. ,-2
C. 人 D.
AA ,所 故答案为A.]
3 . 化简:
4.给出下列四个命题:
①方向相反的两个向量是相反向量;
②若a,b 满足 |a|>|b|且a,b 同向,则a>b;
③不相等的两个空间向量的模必不相等; ④对于任何向量a,b, 必 有 |a+b| ≤|a|+b|. 其中正确命题的序号为
④ [对于①,长度相等且方向相反的两个向量是相反向量,故
①错;对于②,向量是不能比较大小的,故不正确;对于③,不相
等的两个空间向量的模也可以相等,故③错;只有④正确.]
5.设两非零向量e ,e 不共线,且ke +e 与 e +ke 共线,求k
的值.
[解] ∵两非零向量e ,e 不共线,且ke +e 与e +ke 共线,
∴ke +e =t(e +ke ), 则(k—t)e +(1—tk)e =0.
∵非零向量e ,e 不共线,∴k—t=0,1—kt=0, 解得k=±1.
点击右图进入…
Thankyou for watching!
第一章空间向量与立体几何
1. 1 空间向量及其运算
1.1.1 空间向量及其线性运算
学 习 目 标
核 心 素 养
1.理解空间向量的概念.(难点) 2.掌握空间向量的线性运算.(重 点 ) 3.掌握共线向量定理、共面向量 定理及推论的应用.(重点、难 点 )
1.通过空间向量有关概念的学习,
培养学生的数学抽象核心素养.
2.借助向量的线性运算、共线向量
及共面向量的学习,提升学生的直
观想象和逻辑推理的核心素养.
.情景导学:探、新知
情境引入·助学助教
国庆期间,某游客从上海世博园(O)游览结束后乘车到外滩(A)观
赏黄浦江,然后抵达东方明珠(B)游玩,如图1,游客的实际位移是什
么 可以用什么数学概念来表示这个过程
如果游客还要登上东方明珠顶端(D)俯瞰上海美丽的夜景,如图
2,那么他实际发生的位移是什么 又如何表示呢
新知初探一
1.空间向量
(1)定义:在空间,具有大小和方向的量叫做空间向量.
(2)长度或模:空间向量的大小.
(3)表示方法:
①几何表示法:空间向量用有向线段表示;
②字母表示法:用字母a,b,c, … 表示;若向量a 的起点是A,
终点是B, 也可记作:AB, 其模记为la 或 B
名称 方向 模
记法
零向量 任意 0
0
单位向量 任意 1
相反向量 相反 相等
a的相反向量: —a
AB的相反向量:BA
相等向量 相同 相等
a=b
2.几类常见的空间向量
空间向量的 运算 加法 OB=OA+Oc=a+b
减法 CA= OA-OC=a-b
加法运算律 ①交换律:a-十 b = ②结合律: +a Fc)
3.空间向量的线性运算
(1)向量的加法、减法
(2)空间向量的数乘运算
①定义:实数λ与空间向量a 的乘积λa 仍然是一个向量,称为
向量的数乘运算.
当λ>0时, λa 与向量a 方向相同;
当λ<0时, λa 与向量a 方 向相反;
当λ=0时, λa= 0 ;λa 的长度是a 的长度的风 _倍.
②运算律
a. 结合律:λ(μa)=μ(λa)=(λu)a.
b. 分配律:(λ+μ)a=λa+μa,λ(a+b)=λa+λb.
思考:向量运算的结果与向量起点的选择有关系吗
提示没有关系.
4.共线向量
(1)定义:表示若干空间向量的有向线段所在的直线
互相平行或重合,则这些向量叫做共线向量或平行向量.
(2)方向向量:在直线1上取非零向量a, 与 向 量a 平行的非零向
量称为直线l 的方向向量.
规定:零向量与任意向量平行,即对任意向量a, 都有0//a.
(3)共线向量定理:对于空间任意两个向量a,b(b≠0),a// b 的
充要条件是存在实数λ使a=λb .
(4)如图,O 是直线l上一点,在直线l上取非零向量a, 则对于
直线l 上任意一点P, 由数乘向量定义及向量共线的充要条件可知,
存在实数入,使得OP=λa.
5.共面向量
(1)定义:平行于同一个平面的向量叫做共面向量.
(2)共面向量定理:若两个向量a,b 不共线,则向量p 与向量a,
b 共面的充要条件是存在唯一的有序实数对(x,y), 使p=xa+yb.
(3)空间一点P 位于平面ABC 内的充要条件:存在有序实数对(x,
y), 使AP= xAB+yAC 或对空间任意一 点0,有oP=OA+xAB+yAC
思 考:(1)空间中任意两个向量一定是共面向量吗
(2)若空间任意一点O 和不共线的三点A,B,C, 满足
则点P 与 点A,B,C 是否共面
为同一个平面的两个向量,因此一定是共面向量.
(2)由op=s0A+soB+sOC 得op-oA=(oB-oA
OA)
因此点P 与 点A,B,C 共面 .
[提示] (1)空间中任意两个向量都可以平移到同一个平面内,成
初试身手一
1. 思考辨析(正确的打“√ ”,错误的打“×”)
(1)空间向量a,b,c, 若 a//b,b //c,则a//c.
(2)相等向量一定是共线向量.
(3)三个空间向量一定是共面向量.
(4)零向量没有方向.
( )
( )
( )
( )
[提示] ( 1 ) × 若b=0 时 ,a 与 c 不一定平行.
(2) √ 相等向量一定共线,但共线不一定相等.
(3)×空间两个向量一定是共面向量,但三个空间向量可能是
共面的,也可以是不共面的.
(4)× 零向量有方向,它的方向是任意的.
2.如图所示,在四棱柱ABCD-A B C D 所有的棱中,可作为直
线A B 的方向向量的有( )
A.1 个 B.2 个 C.3 个 D.4
D [共四条AB,A B ,CD,C D .]
个
[因为 C 在线段AB 上,所以AB与BC方向相反,又因|AB
=5,|BC|=3,故
3 . 点C 在线段AB上,且AB|=5,|BC|=3,AB=λBC, 则λ=
0 [延长DE交边BC于
点F, 连接AF, 则有
BC=AF,
DF=AF, 故
DE-AD=0.]
4.在三棱锥A-BCD中,若△BCD
是正三角形,E 为其中心,则
化简的结果为 .
合.作.探究.释、疑:难
【例1】 (1)给出下列命题:
①若|a|=|b|,则 a=b 或a=—b;
②若向量a 是向量b 的相反向量,则|a|=|b;
③在正方体ABCD-A B C D 中 ,AC=A C1;
④若空间向量m, n,p 满足m=n , n=p, 则 m=p.
其中正确命题的序号是 .
类 型1 空间向量的有关概念
(2)如图所示,在平行六面体ABCD-A'B'C'D'中,顶点连接的向量
中,与向量AA'相等的向量有 ;与向量AB '相反的向量有
.(要求写出所有适合条件的向量)
(1)②③④ (2)BB',Cc,DD′BA',BA,CD,CD′ [(1)对于
①, 向 量a 与 b 的方向不一定相同或相反,故①错;
对于②,根据相反向量的定义知|a|=|b|,故②正确;
对于③,根据相等向量的定义知,AC=A C , 故③正确;
对于④,根据相等向量的定义知正确.
(2)根据相等向量的定义知,与向量AA'相等的向量有BB',CC
DD.与向量AB'相反的向量有BA',BA,CD,CD'.]
规律方法
解答空间向量有关概念问题的关键点及注意点
(1)关键点:紧紧抓住向量的两个要素,即大小和方向.
(2)注意点:注意一些特殊向量的特性.
①零向量不是没有方向,而是它的方向是任意的,且与任何向
量都共线,这一点说明了共线向量不具备传递性.
规律方法
②单位向量方向虽然不一定相同,但它们的长度都是1.
③两个向量模相等,不一定是相等向量;反之,若两个向量相
等,则它们不仅模相等,方向也相同.若两个向量模相等,方向相反,
则它们为相反向量.
[跟进训练]
1.下列关于空间向量的命题中,正确命题的个数是( )
①长度相等、方向相同的两个向量是相等向量;
②平行且模相等的两个向量是相等向量;
③若a≠b , 则| a|≠|b|;
④两个向量相等,则它们的起点与终点相同.
A.0 B.1 C.2 D.3
B [根据向量的定义,知长度相等、方向相同的两个向量是相等
向量,①正确;平行且模相等的两个向量可能是相等向量,也可能是
相反向量,②不正确;当a=—b 时,也有|a|=|b,③ 不正确;只要
模相等、方向相同,两个向量就是相等向量,与向量的起点与终点无 关,④不正确.综上可知只有①正确,故选B.]
式中运算结果为向量AC 的有( )
① B+BC
C ;
③(AB+BB )+B C ;
1B B C .
A.1 个 B.2 个 C.3 个 D.4 个
类 型2 空间向量的线性运算
【例 2】 (1)如图所示,在正方体 ABCD-A B C D 中,下列各
(2)已知正四棱锥P-ABCD,O 是正方形 ABCD 的中心,Q 是 CD
的中点,求下列各式中x,y,z 的值 .
①0Q=PQ+yPC+zPA;
②PA=xPO+yPQ+PD.
[思路探究] (1)合理根据向量的三角形和平行四边形法则,以及
在平行六面体中,体对角线向量等于从同一起点出发的三条棱向量的
和 . 如AC =AB+AD+AA1.
(2)根据数乘向量及三角形或平行四边形法则求解.
(1)D [对于①,(AB+BC)+Cc =AC+CC =AC ;
对 于 ② ,(AA +A D )+D C =AD +D C =AC ;
对 于 ③ ,(AB+BB )+B C =AB +B C =AC ;
对 于 ④ ,(AA +A B )+B C =AB +B C =AC .]
②∵ 0 为AC的中点,Q 为 CD的中点,
∴PA+PC=2PO,PC+PD=2PQ,
∴PA=2PO-PC,PC=2PQ-PD,
∴PA=2PO-2PQ+PD,∴x=2,y=-2.
规律方法
1.空间向量加法、减法运算的两个技巧
(1)巧用相反向量:向量减法的三角形法则是解决空间向量加法、
减法的关键,灵活运用相反向量可使向量首尾相接.
(2)巧用平移:利用三角形法则和平行四边形法则进行向量加、
减法运算时,务必注意和向量、差向量的方向,必要时可采用空间向
量的自由平移获得运算结果.
规律方法
2.利用数乘运算进行向量表示的技巧
(1)数形结合:利用数乘运算解题时,要结合具体图形,利用三
角形法则、平行四边形法则,将目标向量转化为已知向量.
(2)明确目标:在化简过程中要有目标意识,巧妙运用中点性质.
[跟进训练]
2.已知空间四边形ABCD, 连接AC,BD, 设 M,G 分别是BC,
CD的中点,则MG-AB+AD 等于( )
A. B.3MG C.3GM D.2MG
B [MG-AB+AD=MG-(AB-AD)=MG-DB
=MG+BD=MG+2MG=3MG.]
类型37 共线问题
【 例 3 】( 1 ) 设 e ,e 是空间两个不共线的向量,已知AB=e
+ke ,BC=5e +4e ,DCc=—e -2e , 且A,B,D 三点共线,实数
k= _.
(2)如图所示,已知四边形ABCD,ABEF 都是平行四边形且不共
面 ,M,N 分别是AC,BF 的中点,判断CE与MN是否共线.
思 论究 (1)根据向量共线的充要条件求解.
(2)根据数乘向量及三角形法则,把MN表示成λCE的形式,再根
据向量共线的充要条件求解.
(1)1 [AD=AB+BC+CD=(e +ke )+(5e +4e )+(e +2e )=
7e +(k+6)e .
设AD=λAB,则 7e +(k+6)e =λ(e +ke )
所 ,解得k=1.]
以上
两式相加得CE=2MN,
所以CE//MN, 即 CE 与MN 共线.
(2)[解] 法 一:因为 M,N 分别是 AC,BF 的中点,且四边形
ABCD,四边形ABEF都是平行四边形,所以
法二:因为四边形 ABEF 为平行四边形,所以连接 AE 时 ,AE
必过点N.
∴CE=AE-AC=2AN—2AM
=2(AN-AM)=2MN.
所以CE//MN, 即 CE 与MN 共线.
● 规 律 方 法
证明空间三点共线的三种思路
对于空间三点P,A,B 可通过证明下列结论来证明三点共线.
(1)存在实数λ,使A=λPB 成立.
(2)对空间任一点O, 有OP=OA+tAB(t∈ R).
(3)对空间任一点O, 有OP=xOA+yOB(x+y=1).
2ED ,F 在对角线A C上 ,
求 证 :E,F,B 三点共线.
3.如图,在正方体ABCD-A B C D 中 ,E 在A D 上,且 A E =
[跟进训练]
[证明] 设AB=a,AD=b,AA =c,
因为A E=2ED , 9
所 9 9
所 所以E,F,B 三点共线.
所以EF=
[探究问题]
1.什么样的向量算是共面向量
[提示] 能够平移到同一个平面内的向量称为共面向量.
类 型 4 向量共面问题
2 . 能说明P,A,B,C 四点共面的结论有哪些
[提示] ( 1)存在有序实数对(x,y), 使得AP=xAB
(2)空间一点P在平面ABC内的充要条件是存在有序实数组(x,
y,z) 使得OP=xOA+yOB+zOC (其中x+y+z=1).
(3)四点中任意两点的方向向量与另外两点的方向向量共线,如
PA//BC.
3 . 已知向量a,b,c 不共面,且p=3a+2b +c,m=a—b+c,
n=a+b—c, 试判断p,m,n 是否共面.
[提示] 设p=xm+yn, 即3a+2b+c=x(a-b+c)+
y(a+b—c)=(x+y)a+ (一x+y)b+(x—y)c.
因为a,b,c 不共面,所以
而此方程组无解,所以p不能用m,n 表示,
即p,m,n 不共面.
【例4】 已 知A,B,C 三点不共线,O 为平面ABC外一点,若
点M 满足
(1)判断MA,MB,M C三个向量是否共面;
(2)判断M 是否在平面ABC 内 .
元(1)根据向量共面的充要条件,即判断是否 MA =
xMB+yMC;(2) 根据(1)的结论,也可以利用OM=xOA+yOB+ zoC
中x+y+z 是否等于1.
[解] (1)∵OA+OB+0c=30M,
∴OA-OM=(OM-OB)+(OM-OC),
∴MA=BM+CM=—MB—MC,
∴向量MA,MB,MC 共面.
(2)由(1)知向量MA,MB,M C共面,而它们有共同的起点M , 且
A,B,C 三点不共线,∴M,A,B,C 共面,即M在平面ABC内 .
1. [变条件] 若把本例中条件
“OA+2OB=6OP-30C”, 点P 是否与点A 、B 、C 共面.
[解]∵3OP-30c=OA+2OB-3OP=(OA
2OP),
∴3CP=PA+2PB,即PA=-2PB-3PC.
根据共面向量定理的推论知:点P 与点A,B,C 共面.
[母题探究]
改为
OB—
2. [变条件] 若把本例条件变成“OP+0C=40A-OB”,
是否与点A 、B 、C 共面.
[解] 设OP=0A+xAB+yAC(x,y∈R), 则
OA+xAB+yAC+0c=40A-OB,
∴OA+x(OB-OA)+y(OC-OA)+0C=40A-OB,
∴(1-x-y-4)OA+(1+x)OB+(1+y)OC=0,
点 P
由题意知OA,OB,OC 均为非零向量,所以x,y 满足:
显然此方程组无解,故点P 与点A,B,C 不
共面.
3.[变解法] 上面两个母题探究,还可以用什么方法判断
[解] ( 1)由题意知,
, 点P与点A 、B 、C共面.
(2)∵OP=40A-OB-OC,而4-1-1=2≠1.
∴点P 与点A 、B 、C 不共面.
·
●规律方法
解决向量共面的策略
(1)若已知点P 在平面ABC内,则有AP=xAB+yAC 或OP=xOA+
yOB+zOC(x+y +z =1), 然后利用指定向量表示出已知向量,用待
定系数法求出参数.
(2)证明三个向量共面(或四点共面),需利用共面向量定理,证
明过程中要灵活进行向量的分解与合成,将其中一个向量用另外两 个向量来表示.
课堂小结. 提素· 养
必 备 素 养一
1.一些特殊向量的特性
(1)零向量不是没有方向,而是它的方向是任意的.
(2)单位向量方向虽然不一定相同,但它们的长度都是1.
(3)两个向量模相等,不一定是相等向量,反之,若两个向量相
等,则它们不仅模相等,方向也相同.若两个向量模相等,方向相
反,则它们为相反向量.
2.OP=OA+xAB+yAC 称为空间平面ABC的向量表达式.由此
可知空间中任意平面由空间一点及两个不共线向量唯一确定.
3.证明(或判断)A,B,C 三点共线时,只需证明存在实数λ,使
AB=λBC (或AB= λAC)即可,也可用“对空间任意一点O, 有 0c =
tOA+(1-t)OB” 来证明A,B,C 三点共线.
4. 空间一点P 位于平面MAB内的充要条件是存在有序实数对
(x,y), 使 MP=x MA +y MB, 满足这个关系式的点都在平面MAB
内;反之,平面MAB内的任一点都满足这个关系式.这个充要条件
常用于证明四点共面.
5.直线的方向向量是指与直线平行或共线的非零向量, 一条直
线的方向向量有无穷多个,它们的方向相同或相反.
6 . 向量p与向量a,b 共面的充要条件是在a 与b不共线的前提下
才成立的,若a 与b共线,则不成立.
MC=0 得MA=—MB—
MC ,故M,A,B,C 共
面 . ]
学以致用一
1.下列条件中使M与A,B,C
共面的是( )
A.OM=20A-OB-OC
C.MA+MB+MC=0
D.OM+OA+OB+OC=0
C [由MA+ MB +
一定
2. 已知正方体ABCD-A B C D , 若 点F 是侧面CD 的中心,且
AF=AD+mAB-nAA , 则m,n 的值分别为( )
A. ,-2 B. ,-2
C. 人 D.
AA ,所 故答案为A.]
3 . 化简:
4.给出下列四个命题:
①方向相反的两个向量是相反向量;
②若a,b 满足 |a|>|b|且a,b 同向,则a>b;
③不相等的两个空间向量的模必不相等; ④对于任何向量a,b, 必 有 |a+b| ≤|a|+b|. 其中正确命题的序号为
④ [对于①,长度相等且方向相反的两个向量是相反向量,故
①错;对于②,向量是不能比较大小的,故不正确;对于③,不相
等的两个空间向量的模也可以相等,故③错;只有④正确.]
5.设两非零向量e ,e 不共线,且ke +e 与 e +ke 共线,求k
的值.
[解] ∵两非零向量e ,e 不共线,且ke +e 与e +ke 共线,
∴ke +e =t(e +ke ), 则(k—t)e +(1—tk)e =0.
∵非零向量e ,e 不共线,∴k—t=0,1—kt=0, 解得k=±1.
点击右图进入…
Thankyou for watching!
