6.3.1 二项式定理课件设计超好用的优秀公开课获奖课件(共25张PPT)-人教A版高中数学(2019)选择性必修三
文档属性
| 名称 | 6.3.1 二项式定理课件设计超好用的优秀公开课获奖课件(共25张PPT)-人教A版高中数学(2019)选择性必修三 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 12:43:57 | ||
图片预览








文档简介
(共25张PPT)
人教A版2019高中数学选择性必修三
6 . 3二项式定理
情景导入
如果按2021年山东省的国内生产总值为8.3万
亿,年增长率为8.3%那么10年后,我省的国内 生产总值将达到多少万亿
8.3(1+8.3%)10=
第六章 计数原理
6.3二项式定理
6.3.1 二项式定理
预习情况反馈
学 习 目 标
核 心 素 养
1.能用计数原理推导二项式定
理 . 2.掌握二项式定理及其二项展开 式的通项公式.(重点)
1.通过二项式定理的学习,培养
逻辑推理的素养.
2.借助二项式定理及展开式的通
3.能解决与二项式定理有关的简 单问题.(重点、难点)
项公式解题,提升数学运算素养.
目标与素养
6
問题引入
什么是二项式,二项式定理研究的是什么
二项式
对于a+b,(a+b) ,(a+b) ,(a+b) , 等代数式,数学
上统称为二项式,其一般形式为: (a+b)n (n∈N*)
在许多代数问题中需要将二项式展开,因此,二项式定理研
究的是(a+b)n展开后的表达式的一般结构。那么(a+b)n 的展开 式是什么呢
复习引入
当 n=1、2、3、4时 , 求(a+b)n 的展开式
(a+b) =a+b
(a+b) = a +2ab+b
(a+b) = (a+b) (a+b)=(a +2ab+b )(a+b)
=a +3a b+3ab +b
(a+b) =(a+b) (a+b)
= (a +3a b+3ab +b )(a+b)
=a +4a b+6a b +4ab +b
(a+b) 00= (a+b)n=
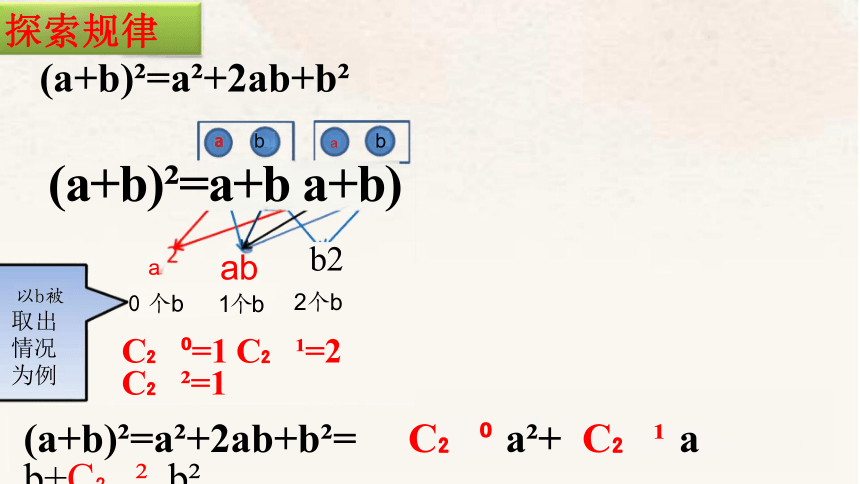
探索规律
(a+b) =a +2ab+b
b a b
(a+b) =a+b a+b)
(a+b) =a +2ab+b = C a + C a b+C b
C =1 C =2 C =1
以b被 取出 情况 为例
ab
1个b
b2
2个b
a
0 个b
(a+b) =(a+b)(g+b)(a+b)
C a C a bC ab C b
(a+b) = C a + C a b+ C ab + C b
探索规律
(a+b) =a +3a b+3ab +b
探索规律
(a+b) = C 'a C Iab +C b
(a+b) =C 0a +C a b+C ab +C 3b
(a+b) =(a+b)(a+b)(a+b)(a+b)
=C a +C a b+C a b +C ab +C Ab
(a+b) 0= Cloa 0+C o a b+C o a b ……+C 010 b 0
(a+b)"=CaOa"+C.lan-1b+Cn an-2b +…+C,kan-kbk…+C",bn
猜想推广
二项式定理
a+b)n=C,0 a"+ Cn1an-1b+Cn a -2b + ±Cnkan -kb ± C"。bn
二项式展开式 二项式系数 通项公式
思考1:二项式定理中的通项公式C,kan-kbk是展开式的第几项
思考2、二项展开式有哪些特点
1.项数规律:展开式共有n+1项
2.二项式系数规律: Cn 、Cn...Ch..·Cn
二项式系数可写成组合数的形式,组合数的下 标为二项式的次数,组合数的上标由0递增到n
3.指数规律:
(1)各项的次数和均为n;
(2)字母a 按降幂排列,次数由n 递减到0
字母b按升幂排列,次数由0递增到n
定理应用,初步体验
题型一:求二项展开式
例1、( 1 ) 求 ( 2 +x) 的展开式
(2)化简:(x—1) +5(x—1) +10(x—1) +10(x—1) +5(x—1)+1.
(1)(2+x)
=C 2 +C 2 x+C 2 x +C 2 x +Cs2x +C x
=32+80x+80x +40x +10x +x
思考:第三项是什么 第 三项的二项式系数,第三 项的系数又是什么
定理应用,初步体验
(2)(x—1) +5(x—1) +10(x—1) +10(x—1) +5(x—1)+1 .
=Cs (x-1) +C (x-1) ·1+C (x-1) 1 +C 3(x-1) -1 +C 4(x-1)·1 +C 15
=[(x-1)+1]5
=x5
公式要正用,逆用,还要变形的用
巩固练习 一
求 的展开式
[解](1)法一:
方法
定理应用,初步体验
题型二:求展开式中的特定项
【例2】 已知 展开式中第3项的系数比第2项的系数
大162.
(1)求n 的值;
(2)求展开式中含x 的项,并指出该项的二项式系数.
依题意,得4C +2C =162, 所以2C +C =81,
所以n =81,n=9.
所以第二项为含x 的 项 ,T =—2Cbx =—18x .
二项式系数为C,=9.
(2)设第r+1 项含x 项,
,r=1,
所
巩固练习二
1.在本例条件不变的情况下,求二项展开式的常数项.所有有
T =(一2) C x-6 —4608x-6;
T1o=(一2) 9x =—512x-9.
3k ∈,
的 有有理项为
∴展开式中的常数项为
9故从可取1,3,5
2
理项.
解
;
思考感悟
1.01365=37.8
0.99365=0.03
积跬步以至千 里,积怠惰以至深 渊
总结归纳
目思维导图
iT
文本样式| 插入多媒体
二项式定理
结构模板
撤销
全屏
(1) 、A 组课本第31页练习1-5
B 组课时分层训练第29页
(2)、牛顿是人类历史上最伟大的物理学家之一,同时他也是个
伟大的天文学家、数学家,在二项式的研究中牛顿也作出了巨
大贡献。请同学们搜集二项式定理的产生、完备和推广所走过
的漫长历程。
作业布置
人教A版2019高中数学选择性必修三
6 . 3二项式定理
情景导入
如果按2021年山东省的国内生产总值为8.3万
亿,年增长率为8.3%那么10年后,我省的国内 生产总值将达到多少万亿
8.3(1+8.3%)10=
第六章 计数原理
6.3二项式定理
6.3.1 二项式定理
预习情况反馈
学 习 目 标
核 心 素 养
1.能用计数原理推导二项式定
理 . 2.掌握二项式定理及其二项展开 式的通项公式.(重点)
1.通过二项式定理的学习,培养
逻辑推理的素养.
2.借助二项式定理及展开式的通
3.能解决与二项式定理有关的简 单问题.(重点、难点)
项公式解题,提升数学运算素养.
目标与素养
6
問题引入
什么是二项式,二项式定理研究的是什么
二项式
对于a+b,(a+b) ,(a+b) ,(a+b) , 等代数式,数学
上统称为二项式,其一般形式为: (a+b)n (n∈N*)
在许多代数问题中需要将二项式展开,因此,二项式定理研
究的是(a+b)n展开后的表达式的一般结构。那么(a+b)n 的展开 式是什么呢
复习引入
当 n=1、2、3、4时 , 求(a+b)n 的展开式
(a+b) =a+b
(a+b) = a +2ab+b
(a+b) = (a+b) (a+b)=(a +2ab+b )(a+b)
=a +3a b+3ab +b
(a+b) =(a+b) (a+b)
= (a +3a b+3ab +b )(a+b)
=a +4a b+6a b +4ab +b
(a+b) 00= (a+b)n=
探索规律
(a+b) =a +2ab+b
b a b
(a+b) =a+b a+b)
(a+b) =a +2ab+b = C a + C a b+C b
C =1 C =2 C =1
以b被 取出 情况 为例
ab
1个b
b2
2个b
a
0 个b
(a+b) =(a+b)(g+b)(a+b)
C a C a bC ab C b
(a+b) = C a + C a b+ C ab + C b
探索规律
(a+b) =a +3a b+3ab +b
探索规律
(a+b) = C 'a C Iab +C b
(a+b) =C 0a +C a b+C ab +C 3b
(a+b) =(a+b)(a+b)(a+b)(a+b)
=C a +C a b+C a b +C ab +C Ab
(a+b) 0= Cloa 0+C o a b+C o a b ……+C 010 b 0
(a+b)"=CaOa"+C.lan-1b+Cn an-2b +…+C,kan-kbk…+C",bn
猜想推广
二项式定理
a+b)n=C,0 a"+ Cn1an-1b+Cn a -2b + ±Cnkan -kb ± C"。bn
二项式展开式 二项式系数 通项公式
思考1:二项式定理中的通项公式C,kan-kbk是展开式的第几项
思考2、二项展开式有哪些特点
1.项数规律:展开式共有n+1项
2.二项式系数规律: Cn 、Cn...Ch..·Cn
二项式系数可写成组合数的形式,组合数的下 标为二项式的次数,组合数的上标由0递增到n
3.指数规律:
(1)各项的次数和均为n;
(2)字母a 按降幂排列,次数由n 递减到0
字母b按升幂排列,次数由0递增到n
定理应用,初步体验
题型一:求二项展开式
例1、( 1 ) 求 ( 2 +x) 的展开式
(2)化简:(x—1) +5(x—1) +10(x—1) +10(x—1) +5(x—1)+1.
(1)(2+x)
=C 2 +C 2 x+C 2 x +C 2 x +Cs2x +C x
=32+80x+80x +40x +10x +x
思考:第三项是什么 第 三项的二项式系数,第三 项的系数又是什么
定理应用,初步体验
(2)(x—1) +5(x—1) +10(x—1) +10(x—1) +5(x—1)+1 .
=Cs (x-1) +C (x-1) ·1+C (x-1) 1 +C 3(x-1) -1 +C 4(x-1)·1 +C 15
=[(x-1)+1]5
=x5
公式要正用,逆用,还要变形的用
巩固练习 一
求 的展开式
[解](1)法一:
方法
定理应用,初步体验
题型二:求展开式中的特定项
【例2】 已知 展开式中第3项的系数比第2项的系数
大162.
(1)求n 的值;
(2)求展开式中含x 的项,并指出该项的二项式系数.
依题意,得4C +2C =162, 所以2C +C =81,
所以n =81,n=9.
所以第二项为含x 的 项 ,T =—2Cbx =—18x .
二项式系数为C,=9.
(2)设第r+1 项含x 项,
,r=1,
所
巩固练习二
1.在本例条件不变的情况下,求二项展开式的常数项.所有有
T =(一2) C x-6 —4608x-6;
T1o=(一2) 9x =—512x-9.
3k ∈,
的 有有理项为
∴展开式中的常数项为
9故从可取1,3,5
2
理项.
解
;
思考感悟
1.01365=37.8
0.99365=0.03
积跬步以至千 里,积怠惰以至深 渊
总结归纳
目思维导图
iT
文本样式| 插入多媒体
二项式定理
结构模板
撤销
全屏
(1) 、A 组课本第31页练习1-5
B 组课时分层训练第29页
(2)、牛顿是人类历史上最伟大的物理学家之一,同时他也是个
伟大的天文学家、数学家,在二项式的研究中牛顿也作出了巨
大贡献。请同学们搜集二项式定理的产生、完备和推广所走过
的漫长历程。
作业布置
