2020新版教材人教A版高中数学必修第一册第一章1.3集合的基本运算 课件(共23张PPT)
文档属性
| 名称 | 2020新版教材人教A版高中数学必修第一册第一章1.3集合的基本运算 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1002.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
1.3集合的基本运算
观察下列各个集合,你能说出集合C 与集合A,B 之间的关系吗
(1) A={1,3,5},B={2,4,6},C={1,2,3,4,5,6}
(2)A={x|x 是有理数},B={x| x是无理数},
C={x|x 是实数}.
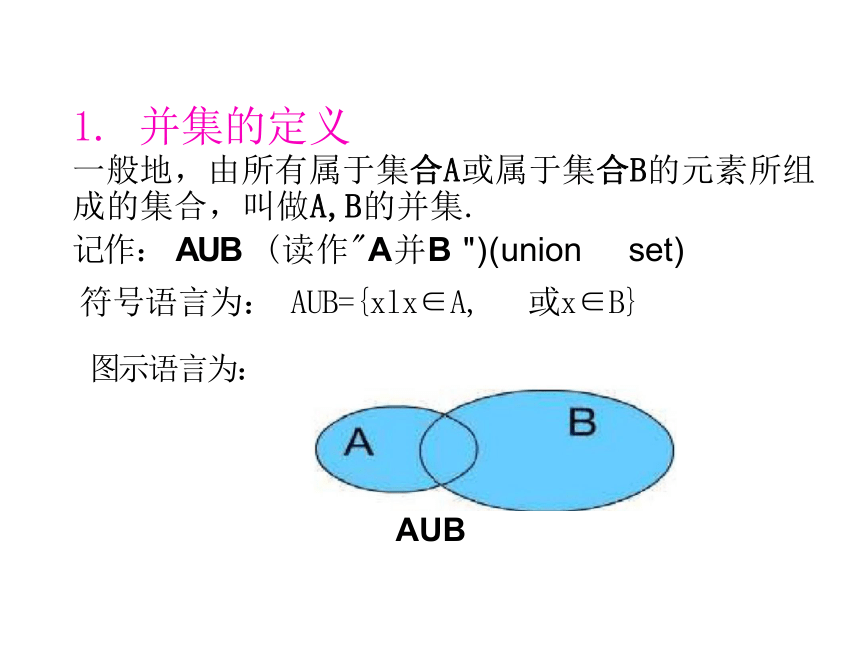
1. 并集的定义
一般地,由所有属于集合A或属于集合B的元素所组
成的集合,叫做A,B的并集.
记作: AUB (读作"A并B ")(union set)
符号语言为: AUB={xlx∈A, 或x∈B}
图示语言为:
AUB
例1 设A={4,5,6,8},B={3,5,7,8}, 求AU B.
解:AUB={4,5,6,8}U {3,5,7,8}
={3,4,5,6,7,8}
例2设集合A={x|-1求AUB.
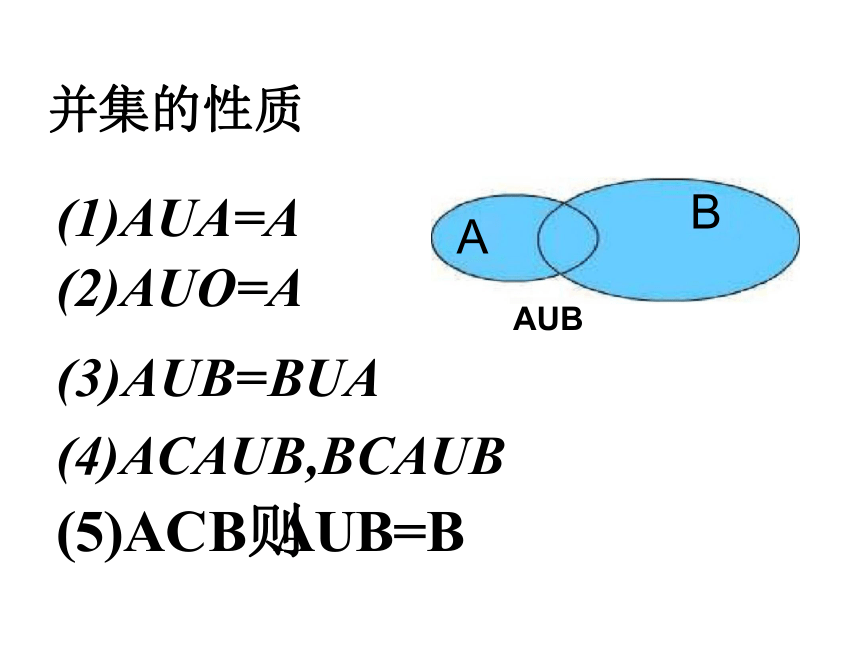
解:AUB={x|-1={x|-1集合B={x|1{x|1(3)AUB=BUA
(4)ACAUB,BCAUB
(5)ACB则AUB=B
并集的性质
(1)AUA=A
(2)AUO=A
B
A
AUB
考察下列各个集合,你能说出集合A,B 与集合C 之间的关系吗
(1)A={2,4,6,8,10},B={3,5,8,12},C={8};
(2)A={x|x 是立德中学今年在校的女同学},
B={x|x 是立德中学今年在校的高一年级同学},
C={x|x 是立德中学今年在校的高一年级女同学}.
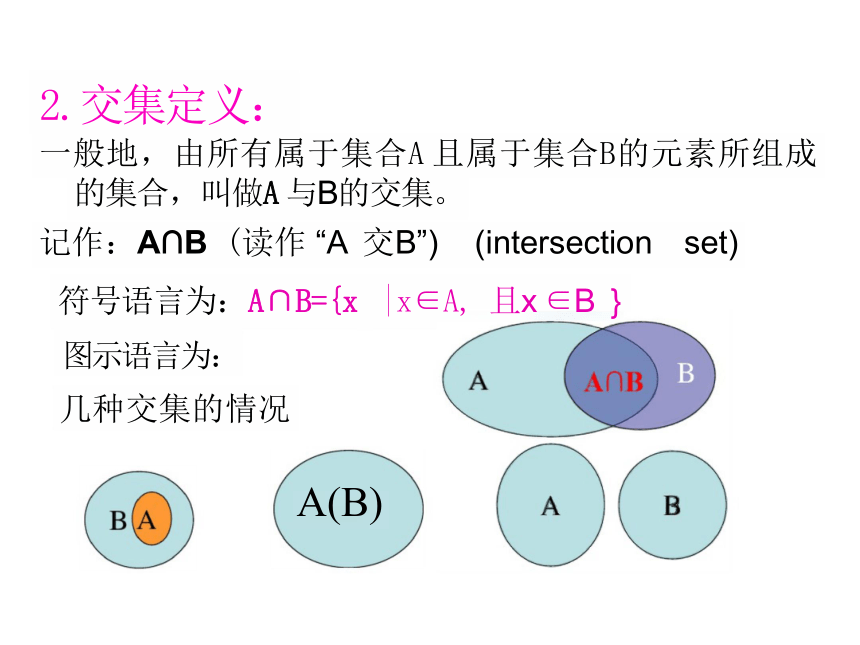
2.交集定义:
一般地,由所有属于集合A 且属于集合B的元素所组成
的集合,叫做A 与B的交集。
记作:A∩B (读作 “A 交B”) (intersection set)
符号语言为:A∩B={x |x∈A, 且x ∈B }
图示语言为:
几种交集的情况
A(B)
例3立德中学开运动会,设
A={x|x 是立德中学高一年级参加百米赛跑的同学}
B={x|x 是立德中学高一年级参加跳高比赛的同学}, 求A∩B.
解:A∩B={x| x 是立德中学高一年级既参加百米赛 跑又参加跳高比赛的同学}.
例4设平面内直线l 上的点的集合为L , 直线l 上点
的集合为L ,试用集合的运算表示lj,l 的位置关系.
解:(1)直线l,l 相交于一点P可表示为
L ∩L ={ 点P};
(2)直线l,l 平行可表示为
L ∩L =0;
(3)直线l,l 重合可表示为
L ∩L =L =L .
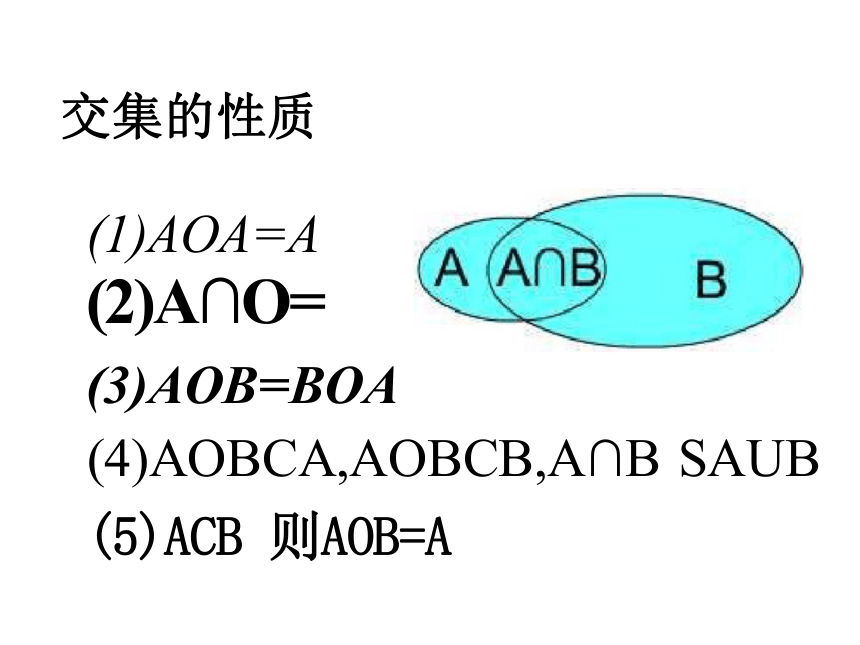
交集的性质
(1)AOA=A
(2)A∩O=
(3)AOB=BOA
(4)AOBCA,AOBCB,A∩B SAUB
(5)ACB 则AOB=A
反馈练习
|x>-2},B={x|x<3},求 ANB,AUB.
解 :ANB={x |x>-2}∩{x|x<3}={x|-21.设A={x
2. 设A={x|-1B
A
AUB
-1 0 1 2 3
解:AUB={x|-1解: A∩B={x |x是等腰三角形}N{x|x 是直角三角 形}={x|x 是等腰直角三角形}
3.设A={x |x是等腰三角形},B={x|x 求A∩B,AUB
是直角三角形},
求AUB.A∩B
提高练习
1.设A={ 三角形},B={ 等腰三角形},C={ 等边三角形},D={ 直 角三角形},则下列关系正确的是 (B)
(A)AUD=D (B)CUB=B (C)CUB=C (D)BUD=B
2.若A={1,3,x},B={x ,1}, 且AUB={1,3,x}, 则这
样不同的x有 (C) 个 .
(A)1 (B)2 (C)3 (D)4
3.设集合M={1,-3,0},N={t -t+1}, 若MUN=M,
则t= 1,0
本课小结
1.交集与并集的概念
2.交集与并集的性质
作业:课本P12 练习1,2,4
1.3集合的基本运算(2)
例:下列各组的三个集合中,哪两个集合之间有包含关系
(1)s={-2,-1,1,2}A={-1,1},B={-2,2};
2)s=R,A={xlx≤0,x∈R},B={xlx>0,x∈R};
(3)s={xlx为地球人},A={lx为中国人},B={xlx为外国 人}
解 在(1)、(2)、(3)中都有AES,BSS,
可用右图来表示
思考观察上例中每一组的三个集合,
它们之间还有一种什么关系
设AcS,由S中不属于A的所有元素组成的集合称为S的
子集A的补集(complementary set),记为[sA(读作"A
中的补集”),即[sA={xlx∈S,且x使A}.
[ A可用右图中的阴影部分来表示 .
对于上例我们有B= [ ,A,A= [ 。B
如果集合S包含我们所要研究的各个集合,这时S可以看
做一个全集(universal) ,全集通常记作U .
例如,在实数范围内讨论集合时,R便可看做一个全集U.
例 1 设U={x|x 是小于9的正整数},A={1,2,3}
B={3,4,5,6},求CuA,CyB.
解:根据题意可知,U={1,2,3,4,5,6,7,8},
所以 CuA={4,5,6,7,8}
CuB={1,2,7,8}.
例2设全集U={x|x 是三角形},A={x|x 是锐
角三角形},B={x| x 是钝角三角形}
求A∩B,Cu(AUB).
解:根据三角形的分类可知
A∩B=,
AUB={xlx 是锐角三角形或钝角三角形},
Cu(AUB)={xlx 直角三角形}.
例3:不等式组 的解集为A,U=R, 求A及
[yA,并把它们分别表示在数轴上.
解 A={xl2x-1>0,且3x-6≤0}={xl1/2[uA={xlx≤1/2,或x>2},在数轴上表示如下
2
反馈演练
1.已知A={xlx -px-2=0},B={xlx +qx+r=0}
且AUB={-2,1,5},A∩B={-2}, 求p,q,r的值。
(解得:p=-1,q=-3,r=-10)
2.设A={-4,2a-1,a },B={a-5,1-a,9},已知A∩B
={9},求a 的值,并求出AUB.
(解得a=-3 且AUB={-8,-4,4,-7,9})
解:∵A∩B={9},∴9∈A
所以a =9 或2a-1=9, 解得a=±3 或a=5
当a=3 时 ,A={9,5,-4},B={-2,-2,9},B中元素违
背了互异性,舍去
当a=-3 时 ,A={9,-7,-4},B={-8,4,9},A∩B={9}
满足题意,故AUB={-7,-4,-8,4,9}.
当a=5 时 ,A={25,9,-4},B={0,-4,9}, 此时A∩B=
{-4,9},与AnB={9} 矛盾,故舍去
综上所述,a=3 且AUB={-7,-4,-8,4,9}.
3.已知A={xlx -3x+2=0},B={xlx -ax+a-1=0}
若AUB=A, 求实数a的值.
4.设集合A={xl-21},B={xla≤x≤b}
若AUB={xlx>-2},A∩B={xl1(解得a=-1,b=3)
当B={1}时
当B={2}时:
当B={1,2}时
综上所述,a=2 或a=3.
解:∵A={1,2},AUB=A,
∴BcA
∴B≠0 或B={1}或B={2}或B={1,2}.
当B≠ 时,△<0,a不存在.
∴a=2
∴a不存在
∴a=3
本课小结
1.交集与并集的概念
2.全集与补集的概念
3.交集与并集的性质
作业:课本P13 T1,T2;P14 T4
1.3集合的基本运算
观察下列各个集合,你能说出集合C 与集合A,B 之间的关系吗
(1) A={1,3,5},B={2,4,6},C={1,2,3,4,5,6}
(2)A={x|x 是有理数},B={x| x是无理数},
C={x|x 是实数}.
1. 并集的定义
一般地,由所有属于集合A或属于集合B的元素所组
成的集合,叫做A,B的并集.
记作: AUB (读作"A并B ")(union set)
符号语言为: AUB={xlx∈A, 或x∈B}
图示语言为:
AUB
例1 设A={4,5,6,8},B={3,5,7,8}, 求AU B.
解:AUB={4,5,6,8}U {3,5,7,8}
={3,4,5,6,7,8}
例2设集合A={x|-1
解:AUB={x|-1
(4)ACAUB,BCAUB
(5)ACB则AUB=B
并集的性质
(1)AUA=A
(2)AUO=A
B
A
AUB
考察下列各个集合,你能说出集合A,B 与集合C 之间的关系吗
(1)A={2,4,6,8,10},B={3,5,8,12},C={8};
(2)A={x|x 是立德中学今年在校的女同学},
B={x|x 是立德中学今年在校的高一年级同学},
C={x|x 是立德中学今年在校的高一年级女同学}.
2.交集定义:
一般地,由所有属于集合A 且属于集合B的元素所组成
的集合,叫做A 与B的交集。
记作:A∩B (读作 “A 交B”) (intersection set)
符号语言为:A∩B={x |x∈A, 且x ∈B }
图示语言为:
几种交集的情况
A(B)
例3立德中学开运动会,设
A={x|x 是立德中学高一年级参加百米赛跑的同学}
B={x|x 是立德中学高一年级参加跳高比赛的同学}, 求A∩B.
解:A∩B={x| x 是立德中学高一年级既参加百米赛 跑又参加跳高比赛的同学}.
例4设平面内直线l 上的点的集合为L , 直线l 上点
的集合为L ,试用集合的运算表示lj,l 的位置关系.
解:(1)直线l,l 相交于一点P可表示为
L ∩L ={ 点P};
(2)直线l,l 平行可表示为
L ∩L =0;
(3)直线l,l 重合可表示为
L ∩L =L =L .
交集的性质
(1)AOA=A
(2)A∩O=
(3)AOB=BOA
(4)AOBCA,AOBCB,A∩B SAUB
(5)ACB 则AOB=A
反馈练习
|x>-2},B={x|x<3},求 ANB,AUB.
解 :ANB={x |x>-2}∩{x|x<3}={x|-2
2. 设A={x|-1
A
AUB
-1 0 1 2 3
解:AUB={x|-1
3.设A={x |x是等腰三角形},B={x|x 求A∩B,AUB
是直角三角形},
求AUB.A∩B
提高练习
1.设A={ 三角形},B={ 等腰三角形},C={ 等边三角形},D={ 直 角三角形},则下列关系正确的是 (B)
(A)AUD=D (B)CUB=B (C)CUB=C (D)BUD=B
2.若A={1,3,x},B={x ,1}, 且AUB={1,3,x}, 则这
样不同的x有 (C) 个 .
(A)1 (B)2 (C)3 (D)4
3.设集合M={1,-3,0},N={t -t+1}, 若MUN=M,
则t= 1,0
本课小结
1.交集与并集的概念
2.交集与并集的性质
作业:课本P12 练习1,2,4
1.3集合的基本运算(2)
例:下列各组的三个集合中,哪两个集合之间有包含关系
(1)s={-2,-1,1,2}A={-1,1},B={-2,2};
2)s=R,A={xlx≤0,x∈R},B={xlx>0,x∈R};
(3)s={xlx为地球人},A={lx为中国人},B={xlx为外国 人}
解 在(1)、(2)、(3)中都有AES,BSS,
可用右图来表示
思考观察上例中每一组的三个集合,
它们之间还有一种什么关系
设AcS,由S中不属于A的所有元素组成的集合称为S的
子集A的补集(complementary set),记为[sA(读作"A
中的补集”),即[sA={xlx∈S,且x使A}.
[ A可用右图中的阴影部分来表示 .
对于上例我们有B= [ ,A,A= [ 。B
如果集合S包含我们所要研究的各个集合,这时S可以看
做一个全集(universal) ,全集通常记作U .
例如,在实数范围内讨论集合时,R便可看做一个全集U.
例 1 设U={x|x 是小于9的正整数},A={1,2,3}
B={3,4,5,6},求CuA,CyB.
解:根据题意可知,U={1,2,3,4,5,6,7,8},
所以 CuA={4,5,6,7,8}
CuB={1,2,7,8}.
例2设全集U={x|x 是三角形},A={x|x 是锐
角三角形},B={x| x 是钝角三角形}
求A∩B,Cu(AUB).
解:根据三角形的分类可知
A∩B=,
AUB={xlx 是锐角三角形或钝角三角形},
Cu(AUB)={xlx 直角三角形}.
例3:不等式组 的解集为A,U=R, 求A及
[yA,并把它们分别表示在数轴上.
解 A={xl2x-1>0,且3x-6≤0}={xl1/2
2
反馈演练
1.已知A={xlx -px-2=0},B={xlx +qx+r=0}
且AUB={-2,1,5},A∩B={-2}, 求p,q,r的值。
(解得:p=-1,q=-3,r=-10)
2.设A={-4,2a-1,a },B={a-5,1-a,9},已知A∩B
={9},求a 的值,并求出AUB.
(解得a=-3 且AUB={-8,-4,4,-7,9})
解:∵A∩B={9},∴9∈A
所以a =9 或2a-1=9, 解得a=±3 或a=5
当a=3 时 ,A={9,5,-4},B={-2,-2,9},B中元素违
背了互异性,舍去
当a=-3 时 ,A={9,-7,-4},B={-8,4,9},A∩B={9}
满足题意,故AUB={-7,-4,-8,4,9}.
当a=5 时 ,A={25,9,-4},B={0,-4,9}, 此时A∩B=
{-4,9},与AnB={9} 矛盾,故舍去
综上所述,a=3 且AUB={-7,-4,-8,4,9}.
3.已知A={xlx -3x+2=0},B={xlx -ax+a-1=0}
若AUB=A, 求实数a的值.
4.设集合A={xl-2
若AUB={xlx>-2},A∩B={xl1
当B={1}时
当B={2}时:
当B={1,2}时
综上所述,a=2 或a=3.
解:∵A={1,2},AUB=A,
∴BcA
∴B≠0 或B={1}或B={2}或B={1,2}.
当B≠ 时,△<0,a不存在.
∴a=2
∴a不存在
∴a=3
本课小结
1.交集与并集的概念
2.全集与补集的概念
3.交集与并集的性质
作业:课本P13 T1,T2;P14 T4
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
