1.4充要条件 课件(共20张PPT)
文档属性
| 名称 | 1.4充要条件 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 498.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 12:50:43 | ||
图片预览








文档简介
(共20张PPT)
第一章集合与常用逻辑用语 1.4充分条件与必要条件
第四节
第五节
课时内容 充分条件与必要条件(共2课时)
全称量词与存在量词(共2课时)
所在位置 教材第17页
教材第26页
新教材 内容分析 通过列举学生熟悉的数学命题, 加深学生对命题的条件与结论的认识 主要以“若p则q”形式的命题为载体 通过考察命题中的条件p与结论q之间 的关系,学习充分条件、必要条件、 充要条件这三个逻辑用语。
全称量词和存在量词是数学中经 常使用的量词,教材通过丰富的 数学实例,介绍了这两类量词的 意 义 ,探究了全称量词命题和存 在量词命题的否定,并鼓励学生 使用新的数学符号,使学生习惯 于运用数学符号语言表达一些数 学内容。
核心素养 培养 通过观察实例,理解充分条件、必要 条件、充要条件的意义 会辨析充分不必要条件、必要不充分 条件、充要条件、既不充分又不必要 条件,体现了逻辑推理的核心素养。
通过数学实例,使学生理解全称 量词、存在量词的意义,体现了 数学抽象的核心素养;会判定命 题的真假,会写出命题的否定, 体现了逻辑推理的核心素养。
教学主线 命题的真假判断
教材分析
本小节内容选自
《普通高中数学必修第一册》
人教A 版(2019)
第一章《集合与常用逻辑用语》
第四节《充分条件与必要条件》 以下是
“常用逻辑用语”的课时安排:
1. 通过对典型数学命题的梳理,理解充要条件的意义,理解数学定义与充要条
件的关系,培养数学抽象的核心素养。
2.会对某些命题的充要条件进行证明,培养逻辑推理的核心素养。
学习目标
重点、难点
重点:理解充要条件的含义
难点:充分性、必要性证明充要条件的关系
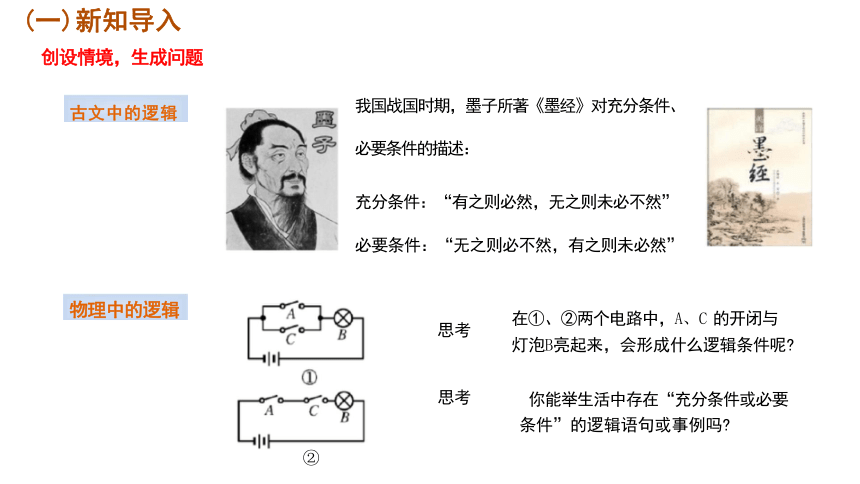
我国战国时期,墨子所著《墨经》对充分条件、
必要条件的描述:
充分条件:“有之则必然,无之则未必不然”
必要条件:“无之则必不然,有之则未必然”
在①、②两个电路中,A、C 的开闭与
灯泡B亮起来,会形成什么逻辑条件呢
你能举生活中存在“充分条件或必要
条件”的逻辑语句或事例吗
(一)新知导入
创设情境,生成问题
物理中的逻辑
古文中的逻辑
思考
思考
②
(一)新知导入
探索交流,解决问题
【问题1】
已 知 p: 整数a是6的倍数,
q: 整数a 是2和3的倍数.
请判断: p是q的充分条件吗
p是q 的必要条件吗
[答案]
p=q, 故p是q 的充分条件,又q>p, 故p
是q的必要条件.
【思考1】
通过判断,你发现了什么
这种关系是否对任意一个“若p, 则q” 的命题
只要具备上述命题的条件都成立
你能用数学语言概括出来吗
[提示]
可以发现: p 既是q的充分条件,又是q的必
要条件,且这种关系对“若p,则q”的命题 只要具备p→q,q→ p都成立,即p→q.
如果“若p, 则q” 和它的逆命题“若q, 则p” 均是真命题,即既有p=q, 又有q=p, 就 记
作__p
此 时 ,p 既是q的充分条件,也是q的必要条件,我们说p是q的 充分必要条件 ,简称为充
要条件(sufficient and necessary condition).显然,如果p是q的充要条件,那么q也是p
的 充要条件
概括地说,如果__p 4 , 那么p与q互为充要条件.
(二)充要条件
(二)充要条件
【思考2】
( 1 ) 如 果p 是q的充要条件,那么p与q是两个相互等价的命题,这种说法对吗
(2)“p 是q的充要条件”与“p的充要条件是q”的区别在哪里
(3)p 是q的条件判断还有什么情况
[答案](1)正确。
(2) p是q的充要条件说明p是条件,q 是结论;p 的充要条件是q说明q是条件,p是结论。
( 3 ) 若p>q, 但qp, 则称p是q的充分不必要条件.
若q>p, 但p q, 则称p是q的必要不充分条件.
若p=q, 且q*p, 则称p是q的既不充分也不必要条件。
(二)充要条件
【辩一辩】 判断正误:
(1)q是p的必要条件时,p 是q的充分条件 . ( √ )
(2)若p是q的充要条件,则命题p和q是两个相互等价的命题.( √)
(3)q不是p的必要条件时,“p=q” 成立 . (v)
【做一—做】
( 1 ) 已 知a,b 是实数,则“a>0且b>0”是“a+b>0, 且ab>0”的 充要 条件.
(2)“x<2” 是 的(A)
A. 充要条件 B. 必要不充分条件
C. 充分不必要条件 D. 既不充分又不必要条件
【解析】
对(1),ab=0 指其中至少有一个为零,而a +b
=0指两个都为零,因此q>p, 但p*q,p 是q的必
要不充分条件;
对(2),|x+yl=|x|+|yl平方得:x +2xy+y =x
+2|xy|+y xy=|xy|=xy≥0, 所以p是q的充要
条件;
对(3),方程x -x-m=0 有实根的充要条件是△= 1+4m>0,m>-, 所以p=q 但q*p,p 是q的充
分不必要条件;
对(4),|x-1|>2=x>3 或X<-1, 所以p*q但
q>p, 所以p是q的必要不充分条件.
【思维引导】
分两个步骤进行判断:
①判断充分性p=q;
(三)充要条件的判断
②判断必要性q=p.
例1 .
记 法 A={x|p(x)},B={x|q(x)} A g B , 且 B g A
关 系 AB)
图示
结论 p 是 q 的 充分不必 要条件 p是q的必 要不充分 条件 p,q互为充 要条件
p是q的既不
充分也不必
要条件
充分、必要条件的判断方法
若p>q, 但q*p, 则称p是q的充分不必要条件.
若q>p, 但p=q, 则称p是q的必要不充分条件. 若p>q, 且q>p, 则称p是q的充要条件。
若p=q, 且q=p, 则 称p是q的既不充分也不必要条件。
(三)充要条件的判断
【类题通法】
1.定义法
2.集合法
(三)充要条件的判断
【巩固练习1】
指出下列各组命题中,p是q 的什么条件(充分不必要条
件,必要不充分条件,充要条件,既不充分又不必要 条件).
(1)p: 数a能被6整除,q: 数a能被3整除;
(2)p:x>1,q:x >1;
(3)p:△ABC 有两个角相等,q:△ABC 是正三角形;
(4)p:|ab|=ab,q:ab>0.
[解析]
(1)∵p→q,q不能推出p,∴p 是q的充分不必要条件.
(2)∵p=q,q 不能推出p,∴p 是q的充分不必要条件. (3)∵p不能推出q,q→p,∴p 是q的必要不充分条件.
(4)∵ab=0时, |ab|=ab,∴“|ab|=ab” 不能推出
“ab>0”, 即p不能推出q.
而当ab>0时,有|ab|=ab, 即q→ p.
∴p是q的必要不充分条件.
(四)充要条件的探求与证明
例2.
[思维引导]从充分性、必要性两方面证明
[证明]
②必要性
(四)充要条件的探求与证明
【类题通法】充要条件的证明分充分性的证明和必要性的证明.
在证明时要注意两种叙述方式的区别:
①p是q的充要条件,则由p>q 证的是充分性,由q=p 证的是必要性;
②p的充要条件是q, 则由p>q 证的是必要性,由q=p 证的是充分性
【巩固练习2】
[证明]
的充要条件是xy>0.
法二: .由条件x>y=y-x<0, 故由
必要性:由 ,得 ,即 .因为x>y,所以y-x<0, 所以xy>0.
法一:充分性:由xy>0及x>y,得 ,即
所 ,即 的充要条件是xy>0.
(四)充要条件的探求与证明
例3. 求关于x的方程ax +2x+1=0 至少有一个负实根的充要条件.
【思维引导】 至少有一个负根可能是一个负根也可能是两个负根,需要分类讨论.
[解析]①当a=0 时,方程为一元一次方程,其根 事 符合要求.
②当a≠0时,方程为一元二次方程,此时 ax +2x+1=0 有实根的充要条件是判别式△≥0,
即4—4a≥0, 从而a≤1.
的两根分别为x ,x , 则
有一负根一正根的充要条件为 →a<0;
设方程ax +2x+1=0
(I) 方程ax +2x+1=0
综上所述,方程ax +2x+1=0 至少有一个负实根的充要条件是a≤1.
有两个负根的充要条件
(Ⅱ)方程ax +2x+1=0
(四)充要条件的探求与证明
【类题通法】 探求充要条件的方法
(1)探求A成立的充要条件时,先将A视为条件,并由A推导结论(设为B),
再证明B是A的充分条件,这样就能说明A 成立的充要条件是B,
即从充分性和必要性两方面说明.
(2)将原命题进行等价变形或转换,直至获得其成立的充要条件,探求的
过程同时也是证明的过程,因为探求过程每一步都是等价的,所以不 需要将充分性和必要性分开来说明.
k<-2
所以使方程x +(2k-1)x+k =0 有两个大于1的实根的充要条件是k<-2.
【巩固练习3】
已知方程x +(2k-1)x+k =0,
[解析方程x +(2k-1)x+k =0
求使方程有两个大于1的实数根的充要条件.
有两个大于1的实数根x ,x
(四)充要条件的探求与证明
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分又不必要条件
3. 已知集合A={1,a},B={1,2,3}, 则 “a=3” 是 “ASB” 的( )
A. 充分不必要条件 B. 必要不充分条件
C.充要条件 D. 既不充分又不必要条件
4.已知a,b 为实数,则“a+b>4” 是“a,b 中至少有一个大于2”的( )
A. 充分不必要条件 B. 必要不充分条件
C.充要条件 D. 既不充分又不必要条件
1. 设 x∈R, 则“1A. 必要不充分条件 B. 充分不必要条件 C. 充要条件
D. 既不充分又不必要条件
2.“x 为无理数”是 “x 为无理数”的( )
(五)操作演练 素养提升
[答案]1 .B 2.B 3.A 4.A
定义 判断 o 如果既有p=q, 又有q→ p, 那么p是 q的充要条件。
定义法
集合法
课堂小结
知识总结
(2)在解决问题时,用到了哪些数学思想
(1)通过这节课,你学到了什么知识
充分条件与 必要条件
学生反思
充分性
必要性
探求与证明
THANKS
第一章集合与常用逻辑用语 1.4充分条件与必要条件
第四节
第五节
课时内容 充分条件与必要条件(共2课时)
全称量词与存在量词(共2课时)
所在位置 教材第17页
教材第26页
新教材 内容分析 通过列举学生熟悉的数学命题, 加深学生对命题的条件与结论的认识 主要以“若p则q”形式的命题为载体 通过考察命题中的条件p与结论q之间 的关系,学习充分条件、必要条件、 充要条件这三个逻辑用语。
全称量词和存在量词是数学中经 常使用的量词,教材通过丰富的 数学实例,介绍了这两类量词的 意 义 ,探究了全称量词命题和存 在量词命题的否定,并鼓励学生 使用新的数学符号,使学生习惯 于运用数学符号语言表达一些数 学内容。
核心素养 培养 通过观察实例,理解充分条件、必要 条件、充要条件的意义 会辨析充分不必要条件、必要不充分 条件、充要条件、既不充分又不必要 条件,体现了逻辑推理的核心素养。
通过数学实例,使学生理解全称 量词、存在量词的意义,体现了 数学抽象的核心素养;会判定命 题的真假,会写出命题的否定, 体现了逻辑推理的核心素养。
教学主线 命题的真假判断
教材分析
本小节内容选自
《普通高中数学必修第一册》
人教A 版(2019)
第一章《集合与常用逻辑用语》
第四节《充分条件与必要条件》 以下是
“常用逻辑用语”的课时安排:
1. 通过对典型数学命题的梳理,理解充要条件的意义,理解数学定义与充要条
件的关系,培养数学抽象的核心素养。
2.会对某些命题的充要条件进行证明,培养逻辑推理的核心素养。
学习目标
重点、难点
重点:理解充要条件的含义
难点:充分性、必要性证明充要条件的关系
我国战国时期,墨子所著《墨经》对充分条件、
必要条件的描述:
充分条件:“有之则必然,无之则未必不然”
必要条件:“无之则必不然,有之则未必然”
在①、②两个电路中,A、C 的开闭与
灯泡B亮起来,会形成什么逻辑条件呢
你能举生活中存在“充分条件或必要
条件”的逻辑语句或事例吗
(一)新知导入
创设情境,生成问题
物理中的逻辑
古文中的逻辑
思考
思考
②
(一)新知导入
探索交流,解决问题
【问题1】
已 知 p: 整数a是6的倍数,
q: 整数a 是2和3的倍数.
请判断: p是q的充分条件吗
p是q 的必要条件吗
[答案]
p=q, 故p是q 的充分条件,又q>p, 故p
是q的必要条件.
【思考1】
通过判断,你发现了什么
这种关系是否对任意一个“若p, 则q” 的命题
只要具备上述命题的条件都成立
你能用数学语言概括出来吗
[提示]
可以发现: p 既是q的充分条件,又是q的必
要条件,且这种关系对“若p,则q”的命题 只要具备p→q,q→ p都成立,即p→q.
如果“若p, 则q” 和它的逆命题“若q, 则p” 均是真命题,即既有p=q, 又有q=p, 就 记
作__p
此 时 ,p 既是q的充分条件,也是q的必要条件,我们说p是q的 充分必要条件 ,简称为充
要条件(sufficient and necessary condition).显然,如果p是q的充要条件,那么q也是p
的 充要条件
概括地说,如果__p 4 , 那么p与q互为充要条件.
(二)充要条件
(二)充要条件
【思考2】
( 1 ) 如 果p 是q的充要条件,那么p与q是两个相互等价的命题,这种说法对吗
(2)“p 是q的充要条件”与“p的充要条件是q”的区别在哪里
(3)p 是q的条件判断还有什么情况
[答案](1)正确。
(2) p是q的充要条件说明p是条件,q 是结论;p 的充要条件是q说明q是条件,p是结论。
( 3 ) 若p>q, 但qp, 则称p是q的充分不必要条件.
若q>p, 但p q, 则称p是q的必要不充分条件.
若p=q, 且q*p, 则称p是q的既不充分也不必要条件。
(二)充要条件
【辩一辩】 判断正误:
(1)q是p的必要条件时,p 是q的充分条件 . ( √ )
(2)若p是q的充要条件,则命题p和q是两个相互等价的命题.( √)
(3)q不是p的必要条件时,“p=q” 成立 . (v)
【做一—做】
( 1 ) 已 知a,b 是实数,则“a>0且b>0”是“a+b>0, 且ab>0”的 充要 条件.
(2)“x<2” 是 的(A)
A. 充要条件 B. 必要不充分条件
C. 充分不必要条件 D. 既不充分又不必要条件
【解析】
对(1),ab=0 指其中至少有一个为零,而a +b
=0指两个都为零,因此q>p, 但p*q,p 是q的必
要不充分条件;
对(2),|x+yl=|x|+|yl平方得:x +2xy+y =x
+2|xy|+y xy=|xy|=xy≥0, 所以p是q的充要
条件;
对(3),方程x -x-m=0 有实根的充要条件是△= 1+4m>0,m>-, 所以p=q 但q*p,p 是q的充
分不必要条件;
对(4),|x-1|>2=x>3 或X<-1, 所以p*q但
q>p, 所以p是q的必要不充分条件.
【思维引导】
分两个步骤进行判断:
①判断充分性p=q;
(三)充要条件的判断
②判断必要性q=p.
例1 .
记 法 A={x|p(x)},B={x|q(x)} A g B , 且 B g A
关 系 AB)
图示
结论 p 是 q 的 充分不必 要条件 p是q的必 要不充分 条件 p,q互为充 要条件
p是q的既不
充分也不必
要条件
充分、必要条件的判断方法
若p>q, 但q*p, 则称p是q的充分不必要条件.
若q>p, 但p=q, 则称p是q的必要不充分条件. 若p>q, 且q>p, 则称p是q的充要条件。
若p=q, 且q=p, 则 称p是q的既不充分也不必要条件。
(三)充要条件的判断
【类题通法】
1.定义法
2.集合法
(三)充要条件的判断
【巩固练习1】
指出下列各组命题中,p是q 的什么条件(充分不必要条
件,必要不充分条件,充要条件,既不充分又不必要 条件).
(1)p: 数a能被6整除,q: 数a能被3整除;
(2)p:x>1,q:x >1;
(3)p:△ABC 有两个角相等,q:△ABC 是正三角形;
(4)p:|ab|=ab,q:ab>0.
[解析]
(1)∵p→q,q不能推出p,∴p 是q的充分不必要条件.
(2)∵p=q,q 不能推出p,∴p 是q的充分不必要条件. (3)∵p不能推出q,q→p,∴p 是q的必要不充分条件.
(4)∵ab=0时, |ab|=ab,∴“|ab|=ab” 不能推出
“ab>0”, 即p不能推出q.
而当ab>0时,有|ab|=ab, 即q→ p.
∴p是q的必要不充分条件.
(四)充要条件的探求与证明
例2.
[思维引导]从充分性、必要性两方面证明
[证明]
②必要性
(四)充要条件的探求与证明
【类题通法】充要条件的证明分充分性的证明和必要性的证明.
在证明时要注意两种叙述方式的区别:
①p是q的充要条件,则由p>q 证的是充分性,由q=p 证的是必要性;
②p的充要条件是q, 则由p>q 证的是必要性,由q=p 证的是充分性
【巩固练习2】
[证明]
的充要条件是xy>0.
法二: .由条件x>y=y-x<0, 故由
必要性:由 ,得 ,即 .因为x>y,所以y-x<0, 所以xy>0.
法一:充分性:由xy>0及x>y,得 ,即
所 ,即 的充要条件是xy>0.
(四)充要条件的探求与证明
例3. 求关于x的方程ax +2x+1=0 至少有一个负实根的充要条件.
【思维引导】 至少有一个负根可能是一个负根也可能是两个负根,需要分类讨论.
[解析]①当a=0 时,方程为一元一次方程,其根 事 符合要求.
②当a≠0时,方程为一元二次方程,此时 ax +2x+1=0 有实根的充要条件是判别式△≥0,
即4—4a≥0, 从而a≤1.
的两根分别为x ,x , 则
有一负根一正根的充要条件为 →a<0;
设方程ax +2x+1=0
(I) 方程ax +2x+1=0
综上所述,方程ax +2x+1=0 至少有一个负实根的充要条件是a≤1.
有两个负根的充要条件
(Ⅱ)方程ax +2x+1=0
(四)充要条件的探求与证明
【类题通法】 探求充要条件的方法
(1)探求A成立的充要条件时,先将A视为条件,并由A推导结论(设为B),
再证明B是A的充分条件,这样就能说明A 成立的充要条件是B,
即从充分性和必要性两方面说明.
(2)将原命题进行等价变形或转换,直至获得其成立的充要条件,探求的
过程同时也是证明的过程,因为探求过程每一步都是等价的,所以不 需要将充分性和必要性分开来说明.
k<-2
所以使方程x +(2k-1)x+k =0 有两个大于1的实根的充要条件是k<-2.
【巩固练习3】
已知方程x +(2k-1)x+k =0,
[解析方程x +(2k-1)x+k =0
求使方程有两个大于1的实数根的充要条件.
有两个大于1的实数根x ,x
(四)充要条件的探求与证明
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分又不必要条件
3. 已知集合A={1,a},B={1,2,3}, 则 “a=3” 是 “ASB” 的( )
A. 充分不必要条件 B. 必要不充分条件
C.充要条件 D. 既不充分又不必要条件
4.已知a,b 为实数,则“a+b>4” 是“a,b 中至少有一个大于2”的( )
A. 充分不必要条件 B. 必要不充分条件
C.充要条件 D. 既不充分又不必要条件
1. 设 x∈R, 则“1
D. 既不充分又不必要条件
2.“x 为无理数”是 “x 为无理数”的( )
(五)操作演练 素养提升
[答案]1 .B 2.B 3.A 4.A
定义 判断 o 如果既有p=q, 又有q→ p, 那么p是 q的充要条件。
定义法
集合法
课堂小结
知识总结
(2)在解决问题时,用到了哪些数学思想
(1)通过这节课,你学到了什么知识
充分条件与 必要条件
学生反思
充分性
必要性
探求与证明
THANKS
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
