高中数学人教版(A版)选择性必修 第二册(2019)_第三章 §3.4 函数中的构造问题 课件(共51张PPT)
文档属性
| 名称 | 高中数学人教版(A版)选择性必修 第二册(2019)_第三章 §3.4 函数中的构造问题 课件(共51张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 00:00:00 | ||
图片预览











文档简介
(共51张PPT)
第三章
§3.4 函数中的构造问题
g(x)=ef(x)
g(x)=x"f(x)
题型一 导数型构造函数
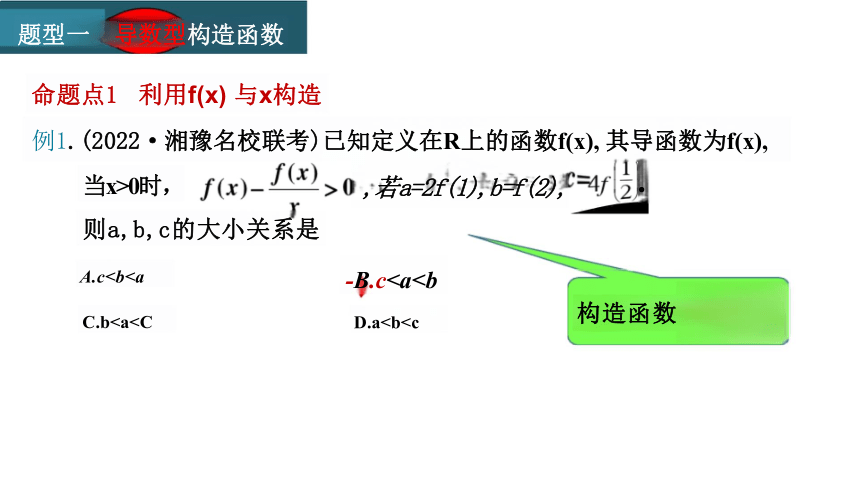
命题点1 利用f(x) 与x构造
例1.(2022·湘豫名校联考)已知定义在R上的函数f(x), 其导函数为f(x),
当x>0时,
则a,b,c的大小关系是
A.cC.b-B.cD.a,若a=2f(1),b=f(2),
构造函数
●
跟踪训练1 设f(x)为定义在R 上的奇函数,f(-3)=0.当x>0 时 ,xf(x)+2f(x)>0,
其中f(x) 为f(x) 的导函数,则使得f(x)>0成立的x的取值范围是
A.(00,-3)U(0,3) B.(-3,0)U(3,+)
C.(-3,0)U(0,3) D.(-00,-3)U(3,+o)
构造函数g(x)=x f(x)
命题点2 利用f(x) 与ex构造
例 2 (多选)已知f(x)是定义在(-00,+0o)上的函数,导函数f(x)满足f(x)对于x∈R 恒成立,则
(2)< 2f(0) B.f(2)>e f(0)
(-1)>f(1) D.e f(-1)构造函数
跟踪训练2 若定义在R 上的函数f(x)满足f(x)+2f(x)>0,且f(0)=1,
则不等 的解集为(0,+oo).
构造函数g(x)=e xf(x)
命题点3 利用f(x)与sin x、cos x构造
例3(多选)(2022·重庆模拟)定义 上的函数f(x),已知f(x) 是它的
构造函数
x:f'(x)+sin x f(x)<0成立,则有
导函数,且恒有cos
跟踪训练3 已知R 上的奇函数f(x),其导函数为f(x), 且当x∈(0,十一)
时 ,f(x)sin x+f(x)cos x<0,若 则a 与b 的大
小关系为 a构造函数
g(x)=sinx f(x)
两道题(构造法)2022.9.8
1.当1e">e, 则( )
A.e >bee-1 B.ea+b>bee C.ae4
两道题(构造法)2022.9.8
1. 当 1e >e, 则 (ABD
A.eb>bee-1 B.ea+b>bee“ C.aeb2.若不等式e +x-a≥Inx+1n(x+1)+a对一切正实数都成立,则实数a 的取值范围是()
A.[-0o,e] B.[-,1] D.[-0,0]
解析:∵e +x-a≥Inx+In(x+1)+a,∴e +×-a-Inx(x+1)-a≥0(x>0)
令t=x +x(t>0), 则∴e “-Int-a≥0(t>0)
令f(t)=e -°-Int-a, 则 (0,+0)单调递增
当t→0时f(t)<0, 当 t→+o 时f(t)>0, 所以存在t。>0, 使得f( )=0, 即
∴f(t)=e-a-Int-a 在(0,t ) 递减,在(t%,+0) 递增,即f(t)mn=e -a-Int 。-a≥0 即可,
, ∴a=to+Int 。,
∴a=t 。+Int ∈(-0,1)
即O两道题(构造法)2022.9.8
1.当1e >e, 则 ( )
A.eb>bee-1 B.ea+b>be° C.aeb原 式 ex x-a>,(x+x)+a
令七二x^2+x
∵XeR ::to
eta ≥, nt+a t>o恒成立
:et-a -lnt-a>0
(t七) =etra -lnt-a t>0)
o)=et-a1
f”=etra+14>0.
't,在切o 单调递增.
2.若不等式e +x-a≥Inx+In(x+1)+a对一切正实数都成立,则实数a 的取值范围是()
A.(- B.(-o,1) D.(-0,0)
t
0-a-a5
恒 成 立
/
单 调 递 甫
单 调 递 增
lta
a≤1
2.若不等式e +x-a≥Inx+In(x+1)+a对一切正实数都成立,则实数a 的取值范围是()
A.(-0,e) B.[-0,1] D.(-0,0)
(6(x +
2
X
例4.(1)若存在x,y∈(0,+00)使得xln(2ax)+y=xlny,则实数a的最大值为
C 口
题型二(同构法构造函数
令 ,g(t)=In t-t,
则
当00, 当t>1时 ,g′(t)<0,
所以g(t)在(0,1)上单调递增,在(1,十一)上单调递减,
所以当t=1 时,
解 析 -
由xln(2ax)+y=xln y,
解 析
g(t)取得极大值即最大值g(1)=—1,
因为当t→0时 ,g(t)→—一,
所以g(t)∈[一一 ,-1],
所以In 2a≤—1,所 以
所以实数a 的最大值
(2022·新高考全国I T7)
7 . 设a=0.1e -4, ,c=-In0.9, 则( C )
A.a同构法
a-c=xex+In(1-x)
a=0.1e .1
Ina-Inb
C=-In 0.9
D.a(2022·新高考全国I T7)
7. 设a=0.1e -4, ,c=-In0.9, 则(C)
A.a解:a=0.1e 4, ,c=-In(1-0.1),
①Ina-lnb=0.1+In(1-0.1),
令f(x)=x+1n(1-x),x∈(0,0.1). 则 单
故f(x)在(0,0.1)上单调递减,可得f(0.1)②a-c=0.1e .1+In(1-0.1),
令g(x)=xe +In(1-x),x∈(0,0.1), 则
令k(x)=(1+x)(1-x)e -1, 所以k′(x)=(1-x -2x)e >0,
所以k(x)在(0.0.1)上单调递增,可得k(x)>k(0)>0, 即 g*(x)>0,
所以g(x)在[0.0.1]上单调递增,可得g(0.1)>g(0)=0,即a-c>0, 所以a>c.
故c(2)(2022·河北联考)已知当x≥e 时,不等式
正实数a 的最小值为
A.1 C.e 口
f(e*)=e-Ine*≤x“-Inx =f(x“)
恒成立,则
同构法的三种基本模式:①乘积型,如ae ≤bln b可以同构
成 ,进而构造函数 ;②比商型,如
可以同构成 ,进而构造函数 ;③和差
型,如e ±a>b±lnb,同构后可以构造函数
思维升华
跟踪训练4 (1)(多选)(2022·常州模拟)若0的是
A.x e>x eX B.x eC.e -e >Inx -In x D.eX -e 在(0,+一)上有且仅有一个零点,则实 数k= 1.
k=xeX-x-Inx
=eInx.ex-x-Inx
=eInx+x-x-Inx
例1.已知函数f(x)=(x+1)In(x+1).若对任意x>0都有f(x)>ax成立,
求实数a 的取值范围.
在解决不等式恒(能)成立,求参数的取值范围这一类问题时,最常用的
方法是分离参数法,转化成求函数的最值,但在求最值时如果出现 型 的代数式,就设法求其最值. 型的代数式,是大学数学中的不定式问 题,解决此类问题的有效方法就是利用洛必达法则.
拓展视野 洛必达法则
法则1 若函数f(x)和g(x)满足下列条件:
(1 ;
(2)在点a 的某去心邻域内,f(x) 与g(x)可导且g′(x)≠0;
那么
法则2 若函数f(x)和g(x)满足下列条件:
(1 ;
(2)在点a 的某去心邻域内,f(x) 与g(x)可导且g′(x)≠0;
那么
例1.已知函数f(x)=(x+1)In(x+1).若对任意x>0都有f(x)>ax成立,
求实数a 的取值范围.
解
方法一令φ(x)=f(x)-ax
=(x+1)ln(x+1)—ax(x>0),
则φ′(x)=1n(x+1)+1—a,
∵x>0,
∴In(x+1)>0.
①当 1 -a≥0, 即a≤1 时,φ′(x)>0,
∴φ(x)在(0,十一)上单调递增,
又φ(0)=0,
解
∴φ(x)>0恒成立,故a≤1满足题意.
②当1—a<0, 即 a>1时,
令φ′(x)=0, 得x=ea-1—1,
∴x ∈(0,ea-1—1) 时,φ′(x)<0;
x∈(ea-1—1,十一)时,φ′(x)>0,
∴φ(x)在(0,ea-1—1) 上单调递减,
在(ea-1—1,十一)上单调递增,
∴φ(x)min=φ(ea-1-1)<φ(0)=0与φ(x)>0恒成立矛盾,故a>1不满足题意
解
综上有a≤1, 故实数a的取值范围是(一0,1).
方法二 当x ∈(0, 十一)时,
(x+1)ln(x+1)>ax 恒成立,
恒成立.
令
令k(x)=x—1n(x+1)(x>0),
∴k(x)在(0,十一)上单调递增.
∴k(x)>k(0)=0,
∴x—1n(x+1)>0恒成立,
∴g'(x)>0, 故g(x)在(0,十一)上单调递增.
∴a≤1, 故实数a 的取值范围是(一一,1) .
解
8.(多选)(2022·山东济宁一中月考)已知定义域为R的函数f(x)的图象
连续不断,且Vx∈R,f(x)+f(-x)=4x ,当x ∈(0,+o)时,f(x)<4x,
若f(2m+1)-f(-m)≤6m +8m+2,则实数m的取值可以为
A.—1
11
12
1 2
4
3
解 析
依题意得,f(x)+f(一x)=4x ,
故f(x)一2x =—[f(一x)-2 (一x) ],
令g(x)=f(x)一2x ,则g(x)=—g(一x),
所以函数g(x)为奇函数,g′(x)=f′(x)一4x,
因为当x∈(0,十一)时,f′(x)<4x,
即当x ∈(0, 十一)时,g'(x)=f'(x) 一4x<0,
故g(x)在(0,十一)上单调递减,由g(x)为奇函数可知,g(x)在R 上单调
递减,
1 2
12
解 析
因为f(2m+1)一f(一m)≤6m +8m+2,
故f(2m+1)-2·(2m+1) ≤f (一m)-2· (一m) ,
即g(2m+1)≤g (一m), 故2m+1≥—m,
则
所以实数m 的取值范围
1 2
12
9.定义在R上的函数f(x)满足:f(x)+f(x)> 1,f(0)=4, 则不等式eYf(x)>e
+3的解集为(0,+) .
①②③ 4 5 10 11 12
解 析
将f(x)+f′( x)>1左右两边同乘e 得,
eYf(x)+eYf'(x)-e>0,
令g(x)=exf(x)-ex,
则g'(x)=eff(x)+exf'(x)—e >0,
所以g(x)在R上单调递增,
且g(0)=f(0)-1=3,
不等式eYf(x)>ex+3等价于eYf(x)-e >3,
即g(x)>g(0),所 以x>0.
12 3 4 10 1 12
10.(2022·江阴模拟)若x①② 3
11 12
4
),于是f(x)在R 上单调递增,
即V y
Vx∈R,
解
因为
即
解析
即
而 最小值一2,即m≤ 一2,
所以实数m 的取值范围是(一一,一2).
11.(2022·深圳模拟)已知a,b,c∈(0,1), 且 a -2ln a+1=e,b -21n b+
2=e ,c -21n c+3=e ,其 中e是自然对数的底数,则a,b,c 的大小关
系是 a>b>c
①②3④5 6 78 9 10 12
解 析
设f(x)=x —21n x,g(x)=ex—x,
则f(a)=g(1),f(b)=g(2),f(c)=g(3),
又g′(x)=ex—1>0(x>0),
所以g(x)在(0,十一)上单调递增,
所以g(3)>g(2)>g(1),
即f(c)>f(b)>f(a),
所以f(x)在(0,1)上单调递减,所以a>b>c.
12 3 4 5
11
12
10
12.若不等式ce -a≥Inx+x-1 恒成立,则实数a 的最大值为 2 .
eInx+x
11
4
6
5
8
12
10
7
2
9
3
1
解析
∵xex—a≥1n x+x—1,
∴eInx+x—a≥1n x+x—1,
令t=1n x+x,
则et—a≥t—1恒成立,
则a≤et—t+1 恒成立,
令φ(t)=et—t+1,
∴φ′(t)=et—1,
1 2 3 12
11
10
解析
当t∈(一一,0)时,φ′(t)<0;
当t∈(0,十 一 )时,φ′(t)>0,
∴φ(t)在(一一,0)上单调递减,在(0,十一)上单调递增,
∴φ(t)min=φ(0)=2,
∴a≤ 2, 故a的最大值为2.
1 10
2
12
拓展冲刺练 见《77练》P278 T4
4.(2022·常德模拟)已知函数f(x)=xe×-x. (1)讨论f(x)的单调性;
(2)证明:当x>0时,f(x)-Inx≥1.
4
2 3
1
解
由题意得f(x)=(x+1)ex—1,
设g(x)=(x+1)ex, 则g'(x)=(x+2)ex,
当x≤ 一 1时,g(x)≤0,f(x)<0,
f(x)在(一一,—1)上单调递减;
当x>—1时 ,g'(x)>0, g(x)单调递增,
又因为g(0)=1,
所以当x<0时 ,g(x)<1, 即f′(x)<0,
当x>0时 ,g(x)>1, 即f′(x)>0,
综上可知,f(x) 在(一0,0)上单调递减,在(0,十一)上单调递增.
①② 3 4
证明
要证f(x)—1nx≥1,
即证xex—x—1n x≥1,
即证ex+Inx—(x+1n x)≥1,
令t=x+1n x,易知t ∈R, 待证不等式转化为
et—t≥1.
设u(t)=et—t, 则u′(t)=et—1,
当t<0时 ,u'(t)<0, 当 t>0时 ,u'(t)>0,
故u(t)在(一0,0)上单调递减,在(0,十一)上单调递增.
所以u(t)≥u(0)=1,原命题得证.
①②3
作业:
1.考前整理
2.准备完成
《讲义》+《77练》3.4
3.选学《洛必达法则》P52
假期作业:
1.完成《77练》P281 T1 、T3
2.完成《讲义》3.5 P53~55
3.4《洛必达法则》
第三章
§3.4 函数中的构造问题
g(x)=ef(x)
g(x)=x"f(x)
题型一 导数型构造函数
命题点1 利用f(x) 与x构造
例1.(2022·湘豫名校联考)已知定义在R上的函数f(x), 其导函数为f(x),
当x>0时,
则a,b,c的大小关系是
A.c
构造函数
●
跟踪训练1 设f(x)为定义在R 上的奇函数,f(-3)=0.当x>0 时 ,xf(x)+2f(x)>0,
其中f(x) 为f(x) 的导函数,则使得f(x)>0成立的x的取值范围是
A.(00,-3)U(0,3) B.(-3,0)U(3,+)
C.(-3,0)U(0,3) D.(-00,-3)U(3,+o)
构造函数g(x)=x f(x)
命题点2 利用f(x) 与ex构造
例 2 (多选)已知f(x)是定义在(-00,+0o)上的函数,导函数f(x)满足f(x)
(2)< 2f(0) B.f(2)>e f(0)
(-1)>f(1) D.e f(-1)
跟踪训练2 若定义在R 上的函数f(x)满足f(x)+2f(x)>0,且f(0)=1,
则不等 的解集为(0,+oo).
构造函数g(x)=e xf(x)
命题点3 利用f(x)与sin x、cos x构造
例3(多选)(2022·重庆模拟)定义 上的函数f(x),已知f(x) 是它的
构造函数
x:f'(x)+sin x f(x)<0成立,则有
导函数,且恒有cos
跟踪训练3 已知R 上的奇函数f(x),其导函数为f(x), 且当x∈(0,十一)
时 ,f(x)sin x+f(x)cos x<0,若 则a 与b 的大
小关系为 a
g(x)=sinx f(x)
两道题(构造法)2022.9.8
1.当1
A.e >bee-1 B.ea+b>bee C.ae
两道题(构造法)2022.9.8
1. 当 1
A.eb>bee-1 B.ea+b>bee“ C.aeb
A.[-0o,e] B.[-,1] D.[-0,0]
解析:∵e +x-a≥Inx+In(x+1)+a,∴e +×-a-Inx(x+1)-a≥0(x>0)
令t=x +x(t>0), 则∴e “-Int-a≥0(t>0)
令f(t)=e -°-Int-a, 则 (0,+0)单调递增
当t→0时f(t)<0, 当 t→+o 时f(t)>0, 所以存在t。>0, 使得f( )=0, 即
∴f(t)=e-a-Int-a 在(0,t ) 递减,在(t%,+0) 递增,即f(t)mn=e -a-Int 。-a≥0 即可,
, ∴a=to+Int 。,
∴a=t 。+Int ∈(-0,1)
即O
1.当1
A.eb>bee-1 B.ea+b>be° C.aeb
令七二x^2+x
∵XeR ::to
eta ≥, nt+a t>o恒成立
:et-a -lnt-a>0
(t七) =etra -lnt-a t>0)
o)=et-a1
f”=etra+14>0.
't,在切o 单调递增.
2.若不等式e +x-a≥Inx+In(x+1)+a对一切正实数都成立,则实数a 的取值范围是()
A.(- B.(-o,1) D.(-0,0)
t
0-a-a5
恒 成 立
/
单 调 递 甫
单 调 递 增
lta
a≤1
2.若不等式e +x-a≥Inx+In(x+1)+a对一切正实数都成立,则实数a 的取值范围是()
A.(-0,e) B.[-0,1] D.(-0,0)
(6(x +
2
X
例4.(1)若存在x,y∈(0,+00)使得xln(2ax)+y=xlny,则实数a的最大值为
C 口
题型二(同构法构造函数
令 ,g(t)=In t-t,
则
当0
所以g(t)在(0,1)上单调递增,在(1,十一)上单调递减,
所以当t=1 时,
解 析 -
由xln(2ax)+y=xln y,
解 析
g(t)取得极大值即最大值g(1)=—1,
因为当t→0时 ,g(t)→—一,
所以g(t)∈[一一 ,-1],
所以In 2a≤—1,所 以
所以实数a 的最大值
(2022·新高考全国I T7)
7 . 设a=0.1e -4, ,c=-In0.9, 则( C )
A.a
a-c=xex+In(1-x)
a=0.1e .1
Ina-Inb
C=-In 0.9
D.a
7. 设a=0.1e -4, ,c=-In0.9, 则(C)
A.a
①Ina-lnb=0.1+In(1-0.1),
令f(x)=x+1n(1-x),x∈(0,0.1). 则 单
故f(x)在(0,0.1)上单调递减,可得f(0.1)
令g(x)=xe +In(1-x),x∈(0,0.1), 则
令k(x)=(1+x)(1-x)e -1, 所以k′(x)=(1-x -2x)e >0,
所以k(x)在(0.0.1)上单调递增,可得k(x)>k(0)>0, 即 g*(x)>0,
所以g(x)在[0.0.1]上单调递增,可得g(0.1)>g(0)=0,即a-c>0, 所以a>c.
故c
正实数a 的最小值为
A.1 C.e 口
f(e*)=e-Ine*≤x“-Inx =f(x“)
恒成立,则
同构法的三种基本模式:①乘积型,如ae ≤bln b可以同构
成 ,进而构造函数 ;②比商型,如
可以同构成 ,进而构造函数 ;③和差
型,如e ±a>b±lnb,同构后可以构造函数
思维升华
跟踪训练4 (1)(多选)(2022·常州模拟)若0
A.x e>x eX B.x e
k=xeX-x-Inx
=eInx.ex-x-Inx
=eInx+x-x-Inx
例1.已知函数f(x)=(x+1)In(x+1).若对任意x>0都有f(x)>ax成立,
求实数a 的取值范围.
在解决不等式恒(能)成立,求参数的取值范围这一类问题时,最常用的
方法是分离参数法,转化成求函数的最值,但在求最值时如果出现 型 的代数式,就设法求其最值. 型的代数式,是大学数学中的不定式问 题,解决此类问题的有效方法就是利用洛必达法则.
拓展视野 洛必达法则
法则1 若函数f(x)和g(x)满足下列条件:
(1 ;
(2)在点a 的某去心邻域内,f(x) 与g(x)可导且g′(x)≠0;
那么
法则2 若函数f(x)和g(x)满足下列条件:
(1 ;
(2)在点a 的某去心邻域内,f(x) 与g(x)可导且g′(x)≠0;
那么
例1.已知函数f(x)=(x+1)In(x+1).若对任意x>0都有f(x)>ax成立,
求实数a 的取值范围.
解
方法一令φ(x)=f(x)-ax
=(x+1)ln(x+1)—ax(x>0),
则φ′(x)=1n(x+1)+1—a,
∵x>0,
∴In(x+1)>0.
①当 1 -a≥0, 即a≤1 时,φ′(x)>0,
∴φ(x)在(0,十一)上单调递增,
又φ(0)=0,
解
∴φ(x)>0恒成立,故a≤1满足题意.
②当1—a<0, 即 a>1时,
令φ′(x)=0, 得x=ea-1—1,
∴x ∈(0,ea-1—1) 时,φ′(x)<0;
x∈(ea-1—1,十一)时,φ′(x)>0,
∴φ(x)在(0,ea-1—1) 上单调递减,
在(ea-1—1,十一)上单调递增,
∴φ(x)min=φ(ea-1-1)<φ(0)=0与φ(x)>0恒成立矛盾,故a>1不满足题意
解
综上有a≤1, 故实数a的取值范围是(一0,1).
方法二 当x ∈(0, 十一)时,
(x+1)ln(x+1)>ax 恒成立,
恒成立.
令
令k(x)=x—1n(x+1)(x>0),
∴k(x)在(0,十一)上单调递增.
∴k(x)>k(0)=0,
∴x—1n(x+1)>0恒成立,
∴g'(x)>0, 故g(x)在(0,十一)上单调递增.
∴a≤1, 故实数a 的取值范围是(一一,1) .
解
8.(多选)(2022·山东济宁一中月考)已知定义域为R的函数f(x)的图象
连续不断,且Vx∈R,f(x)+f(-x)=4x ,当x ∈(0,+o)时,f(x)<4x,
若f(2m+1)-f(-m)≤6m +8m+2,则实数m的取值可以为
A.—1
11
12
1 2
4
3
解 析
依题意得,f(x)+f(一x)=4x ,
故f(x)一2x =—[f(一x)-2 (一x) ],
令g(x)=f(x)一2x ,则g(x)=—g(一x),
所以函数g(x)为奇函数,g′(x)=f′(x)一4x,
因为当x∈(0,十一)时,f′(x)<4x,
即当x ∈(0, 十一)时,g'(x)=f'(x) 一4x<0,
故g(x)在(0,十一)上单调递减,由g(x)为奇函数可知,g(x)在R 上单调
递减,
1 2
12
解 析
因为f(2m+1)一f(一m)≤6m +8m+2,
故f(2m+1)-2·(2m+1) ≤f (一m)-2· (一m) ,
即g(2m+1)≤g (一m), 故2m+1≥—m,
则
所以实数m 的取值范围
1 2
12
9.定义在R上的函数f(x)满足:f(x)+f(x)> 1,f(0)=4, 则不等式eYf(x)>e
+3的解集为(0,+) .
①②③ 4 5 10 11 12
解 析
将f(x)+f′( x)>1左右两边同乘e 得,
eYf(x)+eYf'(x)-e>0,
令g(x)=exf(x)-ex,
则g'(x)=eff(x)+exf'(x)—e >0,
所以g(x)在R上单调递增,
且g(0)=f(0)-1=3,
不等式eYf(x)>ex+3等价于eYf(x)-e >3,
即g(x)>g(0),所 以x>0.
12 3 4 10 1 12
10.(2022·江阴模拟)若x
11 12
4
),于是f(x)在R 上单调递增,
即V y
Vx∈R,
解
因为
即
解析
即
而 最小值一2,即m≤ 一2,
所以实数m 的取值范围是(一一,一2).
11.(2022·深圳模拟)已知a,b,c∈(0,1), 且 a -2ln a+1=e,b -21n b+
2=e ,c -21n c+3=e ,其 中e是自然对数的底数,则a,b,c 的大小关
系是 a>b>c
①②3④5 6 78 9 10 12
解 析
设f(x)=x —21n x,g(x)=ex—x,
则f(a)=g(1),f(b)=g(2),f(c)=g(3),
又g′(x)=ex—1>0(x>0),
所以g(x)在(0,十一)上单调递增,
所以g(3)>g(2)>g(1),
即f(c)>f(b)>f(a),
所以f(x)在(0,1)上单调递减,所以a>b>c.
12 3 4 5
11
12
10
12.若不等式ce -a≥Inx+x-1 恒成立,则实数a 的最大值为 2 .
eInx+x
11
4
6
5
8
12
10
7
2
9
3
1
解析
∵xex—a≥1n x+x—1,
∴eInx+x—a≥1n x+x—1,
令t=1n x+x,
则et—a≥t—1恒成立,
则a≤et—t+1 恒成立,
令φ(t)=et—t+1,
∴φ′(t)=et—1,
1 2 3 12
11
10
解析
当t∈(一一,0)时,φ′(t)<0;
当t∈(0,十 一 )时,φ′(t)>0,
∴φ(t)在(一一,0)上单调递减,在(0,十一)上单调递增,
∴φ(t)min=φ(0)=2,
∴a≤ 2, 故a的最大值为2.
1 10
2
12
拓展冲刺练 见《77练》P278 T4
4.(2022·常德模拟)已知函数f(x)=xe×-x. (1)讨论f(x)的单调性;
(2)证明:当x>0时,f(x)-Inx≥1.
4
2 3
1
解
由题意得f(x)=(x+1)ex—1,
设g(x)=(x+1)ex, 则g'(x)=(x+2)ex,
当x≤ 一 1时,g(x)≤0,f(x)<0,
f(x)在(一一,—1)上单调递减;
当x>—1时 ,g'(x)>0, g(x)单调递增,
又因为g(0)=1,
所以当x<0时 ,g(x)<1, 即f′(x)<0,
当x>0时 ,g(x)>1, 即f′(x)>0,
综上可知,f(x) 在(一0,0)上单调递减,在(0,十一)上单调递增.
①② 3 4
证明
要证f(x)—1nx≥1,
即证xex—x—1n x≥1,
即证ex+Inx—(x+1n x)≥1,
令t=x+1n x,易知t ∈R, 待证不等式转化为
et—t≥1.
设u(t)=et—t, 则u′(t)=et—1,
当t<0时 ,u'(t)<0, 当 t>0时 ,u'(t)>0,
故u(t)在(一0,0)上单调递减,在(0,十一)上单调递增.
所以u(t)≥u(0)=1,原命题得证.
①②3
作业:
1.考前整理
2.准备完成
《讲义》+《77练》3.4
3.选学《洛必达法则》P52
假期作业:
1.完成《77练》P281 T1 、T3
2.完成《讲义》3.5 P53~55
3.4《洛必达法则》
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
