3.1 函数的概念 课件(共63张PPT)
文档属性
| 名称 | 3.1 函数的概念 课件(共63张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 12:52:30 | ||
图片预览




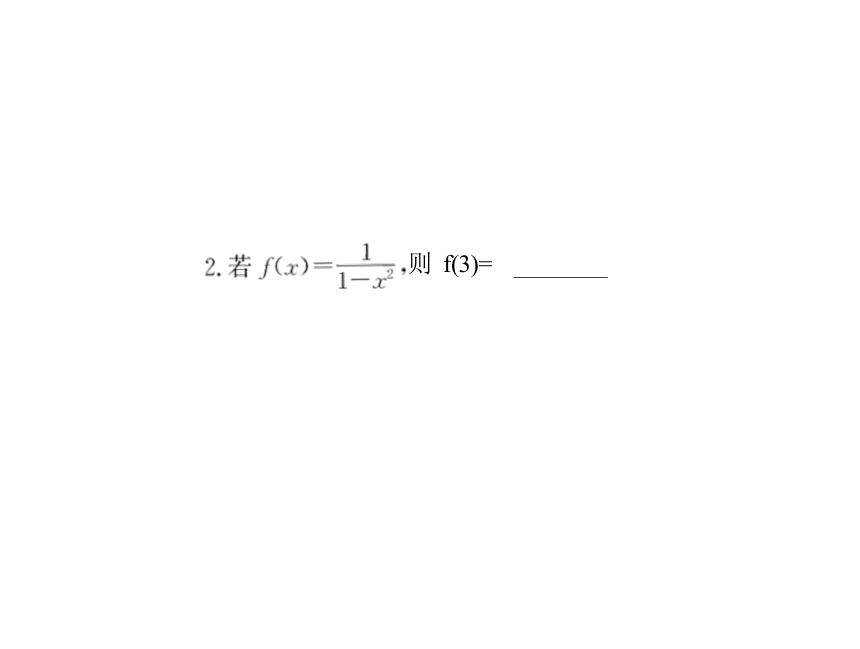




文档简介
(共63张PPT)
第三章 函数的概念与性质
3.1 函数的概念及其表示
3.1.1 函数的概念 第1课时 函数的概念
教师用书配套课性
定 义
设A,B是非空的实数集,如果对于集合A
中的任意一个数x,按照某种确定的对应关 系f,在集合B中都有唯一确定的数y和它 对应,那么就称f:A→B为从集合A到集合 B的一个函数
三 要 素 对应关系
y=f(x),x∈A
定义域
x的取值范围
值域
与x的值相对应的y的值的集合
f(x) ∈A}
基础自主学习
1.函数的概念
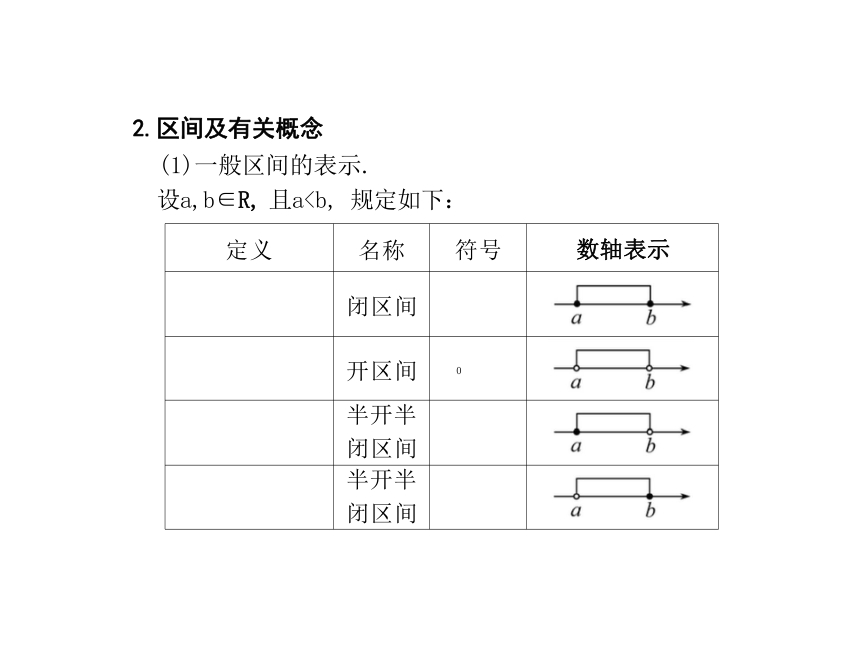
定义 名称 符号
数轴表示
闭区间
开区间 0
半开半 闭区间
半开半 闭区间
2.区间及有关概念
(1)一般区间的表示.
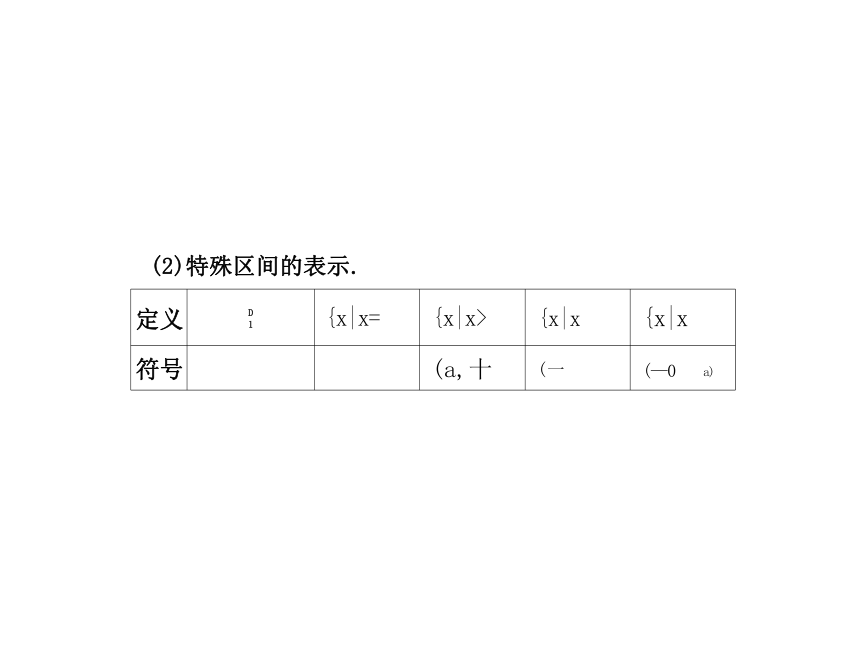
设a,b∈R, 且a定义 D 1 {x|x= {x|x> {x|x
{x|x
符号 (a,十 (一
(—0 a)
(2)特殊区间的表示.
1.思维辨析(对的打“√”,错的打“×”)
(1)“y=f(x)”表示的是“y等于f 与x 的乘积”.( )
(2)根据函数的定义,定义域中的任何一个x 可以对应
着值域中不同的y. ( )
(3)在函数的定义中,集合B 是函数的值域. ( )
(4)在研究函数时,除用符号f(x) 外,还可用g(x),
F(x),G(x) 等来表示函数. ( )
素 养 小 测
提示:(1)×.f(x) 是一个符号,“y=f(x)” 是“y 是
函数”的数学表示.
(2) ×.根据函数的定义,对于定义域中的任何一个
值域中都有唯一的y 与之对应。
(3)×.在函数的定义中,函数的值域是集合B 的子集.
(4) √.同一个题中,为了区别不同的函数,常采用g(x), F(x),G(x) 等来表示函数.
则 f(3)=
3.用区间表示函数 的定义域是
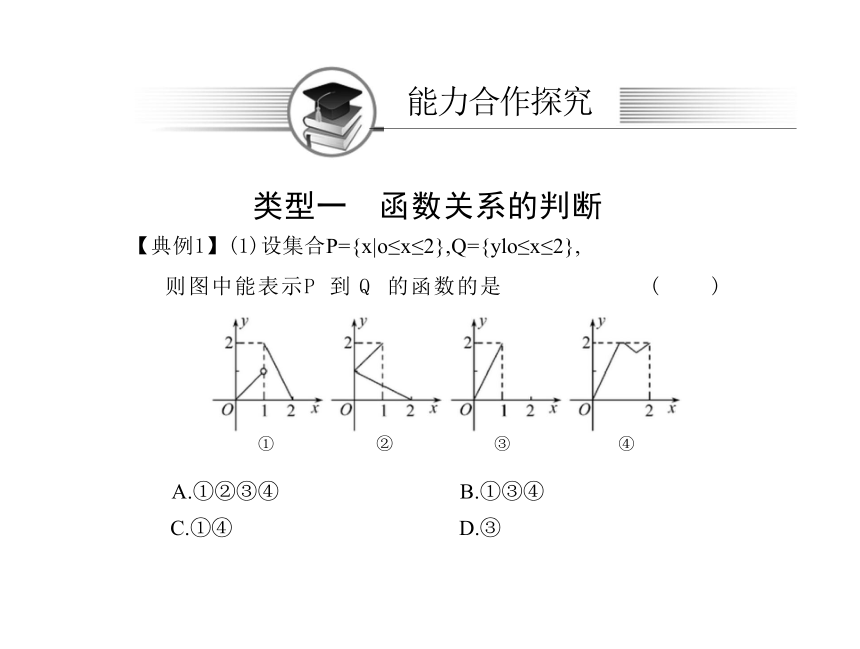
类型一 函数关系的判断
【典例1】(1)设集合P={x|o≤x≤2},Q={ylo≤x≤2},
则图中能表示P 到 Q 的函数的是 ( )
① ② ③ ④
A.①②③④ B.①③④
C.①④ D.③
能力合作探究
②A={x|x>0,x∈R},B={yly∈R}, 对应关系f:x
→y =3x;
③A={x|x∈R},B={yly∈R}, 对应关系f:x→x 十
y =25;
④A=R,B=R, 对应关系f:x→y=x ;
⑤A={(x,y)|x∈R,y∈R},B=R, 对应关系f:(x,y)
→s=x 十y;
⑥A={x|—1≤x≤1,x∈R},B={0}, 对应关系f:x→
y=0.
A.①⑤⑥ B.②④⑤⑥
C.②③④ D.①②③⑤
(2)在下列从集合A 到集合B 的对应关系中,不能确定
y是x 的函数的是 ( )
①A={x|x∈Z},B={yly∈Z}, 对应关系f:x→y
【思维·引】
1.在x 轴上区间[0,2]内作与x 轴垂直的直线,此直线
与函数的图象恰有一个公共点.
2.先看集合A,B 是否为非空数集,再判断非空数集A
中任取一个数,在非空数集 B 中是否有唯一的数与之 对应.
【解析】(1)选C.根据函数的定义,在定义域内的任何一
个x 值,都唯一对应一个y 值,故①、④正确;②中定义 域内的1对应了2个函数值,③中定义域(1,2)内的x 值,没有对应的y 值,故②、③错误.
(2)选D.① 在对应关系f 下 ,A中不能被3整除的数在
B 中没有唯一确定的数与它对应,所以不能确定y 是x 的函数.②在对应关系f 下 ,A 中的数在B 中有两个数 与之对应,所以不能确定y 是x 的函数.③在对应关系 f 下,A 中的数(除去5与一5外)在B 中有两个数与之 对应,所以不能确定y 是 x 的函数.⑤A 不是数集,所 以不能确定y 是x 的 函 数 .④⑥显然满足函数的特征, y 是x 的函数.
两非空实数集A,B
一对一或多对一
A中不能有剩余元素
1.判断一个对应是否是函数的方法
类题 · 通
函数的
概念
作出
判断
2.根据图形判断对应是否为函数的步骤
(1)任做一条垂直于x 轴的直线l.
(2)在定义域内平行移动直线l.
(3)若l 与图形有且只有一个交点,则是函数;若在定义
域内没有交点或有两个或两个以上的交点,则不是函 数.如图所示:
不是函数图象
是函数图象
★习练·破
已知集合A={1,2,3,4},B={5,6,7}, 在下列A 到B 的
四种对应关系中,存在函数关系的个数是 ( )
① ② ③ ④
A.1 B.2 C.3 D.4
A B
A B
【解析】选B.根据函数的定义可知,集合A 中每一个实
数在B 中都有唯一确定的实数与之对应,其中①③均满 足函数的定义.
类型二 求函数的定义域
【典例2】(1)若将长为a 的铁丝折成矩形,则矩形面积 关
于一边长x 的解析式为 ,此函数的定义域 为
(2)求下列函数的定义域.
【思维·引】
(1)先用a 和x 表示另外一条边,然后根据两条边长都
大于0,列不等式组求定义域.
(2)①依据分式的分母不为0,列不等式求定义域。
②依据分式的分母不为0,二次根式的被开方数大于或
等于0,列不等式组求定义域.
【解析】(1)已知矩形的一边长为x, 则另一边长为
—2x),
,故定义域为
由 得
(2)①因为|x+1|≠0,x+1≠0,
所以定义域为{ x|x≠—1}.
所以定义域为{—1}.
所以x≠—1.
②因为
★ 类题·通
已知函数的解析式,求函数的定义域
(1)本质:求使得函数解析式有意义的自变量的取值
范围.
(2)常见题型:
①如果f( x) 是整式,那么函数的定义域是实数集R.
②如 果f(x) 是分式,那么函数的定义域是使分母不等于
零的实数的集合.
③如果f(x) 是二次根式,那么函数的定义域是使根号内
的式子大于或等于零的实数的集合.
④如果y=x°, 那么x≠0.
⑤如果f(x) 是由几个部分的数学式子构成的,那么函数
定义域是使各部分式子都有意义的实数集合(即求各部 分定义域的交集).
⑥对于由实际问题的背景确定的函数,其定义域还要受
实际问题的制约.
★习练·破
求下列函数的定义域:
;(2)y=√x- 1·√ 1—x;
;(4)
③
(1
得函数的定义域为
(2)由 →x=1, 得函数的定义域为{1}.
(3)由
得函数的定义域为{x|x≤1, 且x ≠0}.
(4)因为 ,解得x>—1, 且x≠1.
所以函数的定义域为{x|x>-1, 且x≠1}.
【解析】(1)由
●
的
【加练·固】
求下列函数的定义域.
得x>—2 且 x≠3.
所以所求函数的定义域为(—2,3)U(3, 十 ) .
(2)要使函数有意义,需满足
所以所求函数的定义域为(0,1) U(1, 十一).
【解析】(1)要使函数有意义,需满足
所以x>0 且 x≠1,
即
类型三 函数的对应关系的应用
角度1 求值问题
【典例3】(1)已知f(3x+1)=4x+3, 则 f(4)= ( )
A.6 B.7 C.8 D.9
(2)如图,函数f(x) 的图象是曲线OAB, 其中点O,A,B
的坐标分别为(0,0),(1,2),(3,1),则f(f(3)) 的值为
B
3 x
y
2
1
O
2
【思维·引】
1.注意到f(4)=f(3×1 +1) 就可以利用f(3x+1)=
4x+3 求f(4).
2.根据图象确定自变量x=1 和 x=3 时,对应的函数
值即可求f(f(3)).
【解析】(1)选B.由3x+1=4, 得x=1, 所以f(4)=f(3
×1+1)=4×1+3=7.
(2)据图象知,f(3)=1,f(f(3))=f(1)=2.
答案:2
①求f(3),f(4),f(g(3))及f(g(4))的值.
②求f(g(x)), 并证明f(x)+f(g(x)) 是常数.
角度2 求解析式问题
【典例4】已知函数
●
。
【解析
●
则
类题 · 通
函数求值的方法及关注点
(1)方法.
①求 f(a): 已 知f(x) 的解析式时,只需用a 替换解析式
中的x 即得f(a) 的值.
②求f(g(a)): 已 知f(x) 与 g(x), 求 f(g(a)) 的值应遵
循由里往外的原则.
(2)关注点:用来替换解析式中x 的 数a 必须是函数定
义域内的值,否则函数无意义.
习练 · 破
1.若f(x)=ax —√2,a
为正实数,且f(f(√2))=—√2, 则
a=
2.设f(x)=2x +2, ●
( 1 ) 求 f(2),f(a+3),g (a)+g(0)(a≠
—2),g(f(2)).
(2)求g(f(x)).
≠—2),
【加练·固】
若 (x≠—1), 求 f(0),f(1),
f(1—a)(a≠2),f(f(2)) 的值.
课堂达标检测
1.下列图形中,不能确定y 是x 的函数的是 ( )
y
3
x
B.
C. D.
3
A.
【解析】选D.任作一条垂直于x 轴的直线x=a, 移动直
线,根据函数的定义可知,此直线与函数图象至多有一 个交点.结合选项可知D 不满足要求,因此不表示函数 关系.
2.设函数f(x)=ax+b, 若f(1)=—2,f(—1)=0, 则
( )
A.a=1,b=— 1 B.a=— 1,b=— 1
C.a=—1,b=1 D.a=1,b=1
3.用区间表示数集{xlx≤2 或x>3} 为
,且 f(a)=2, 则 a=
若两个函数的对应关系相同,值域也相同,但定义域不
同,则称这两个函数为同族函数.那么与函数y=x ,x∈
{—1,0,1,2}为同族函数的个数有 ( )
A.5 个 B.6 个 C.7 个 D.8 个
新情境 · 新思维
【解析】选D. 由题意知同族函数是只有定义域不同的函
数,函数解析式为y=x , 值域为{0,1,4}时,定义域中,0 是肯定有的,正负1,至少含一个,正负2,至少含一个.它 的定义域可以是{0,1,2},{0,1,—2},{0,—1,2},{0, — 1,—2},{0,1,—2,2},{0,—1,—2,2},{0,1,—1, —2},{0,1,—1,2,—2},共有8种不同的情况,所以 D 选项是正确的.
函数的概念
基础练
一、选择题
1.设f:x→x 是集合A 到集合B 的函数,如果集合B=
{1},那么集合A 可能是 ( )
A.{1} B.{0}
C.{—1,1,0} D.{—1,0}
课时素养评价(十六)
A.(—1,2)U(2, 十○) B.(—1, 十 )
C.(—1,2) D.(—1, 十 )
2.函数 的定义域为
( )
【加练·固】已知集合A={x|x≥4},
的定义域为B, 若 A∩B=
,则实数a 的取值范围是 ( )
A.(—2,4) B.(3, 十 )
C. ( 一 , 3 ) D. ( 一 , 3 )
3.设M={x|o≤x≤2},N={ylo≤y≤2}, 给出以下四个
图形,其中能表示集合M 到集合N 的函数关系的有
( )
(1) (2) (3) (4)
A.0 个 B.1 个 C.2 个 D.3 个
【解析】选C.图象(1)中,集合M 内(1,2)的元素在集合
N 内没有对应元素,所以图象(1)不能表示集合M 到集 合N 的函数关系;图象(2)中,集合M 内的任意元素在 集合N 中都有唯一确定的对应元素,所以图象(2)能表 示集合M 到集合N 的函数关系;图象(3)中,集合M 内的任意元素在集合N 中都有唯一确定的对应元素, 所以图象(3)能表示集合M 到集合N 的函数关系;图 象(4)中,集合M 内的元素在集合N 中对应的元素不 唯一,所以图象(4)不能表示集合M 到集合N 的函数 关系.所以能表示集合M 到集合N 的函数关系的是 (2)、(3).
4.设f(x)=|x—1|—|x|,
B.0
则 等于
C.1
( )
A
口
【加练·固】已知函数 ,则
( )
B. C.a D.3a
A
二、填空题
5.(2a,3a—1) 为一确定的区间,则 a 的取值范围
是
6.已知函数 ,则g(x)=
,函数g(x) 的定义域是 .(用区间表
示 )
【加练·固】已知等腰△ABC 的周长为
10,底边长y 关于腰长x 的函数关系式为y=
10—2x,则此函数的定义域为
(1)求函数f(x) 的定义域;(2)求f(—1),f(12) 的值.
三 、解答题
能力练
1.给定的下列四个式子中,能确定y 是x 的函数的是
( )
A.x +y =1 B.|x—1|+√y -1=0
C.√x—1+√y-1=1 D.y=√x—3+√2—x
【解析】选C.A. 由x +y =1, 得y=± √1-x , 不满足
函数的定义,所以A 不是函数.B.由 |x—1|+√y -1=
0得, |x—1|=0,√y -1=0, 所以x=1,y=±1, 所以
B不是函数.C. 由√ x—1+√y-1 =1, 得 y=(1— √x—1) +1, 满足函数的定义,所以C 是函数.D. 要使 函数y=√x—3+ √2—x有意义,则 解得 此时不等式组无解,所以D 不是函数.
2.下列函数中,不满足f(2x)=2f(x) 的是 ( )
A.f(x)=|x| B.f(x)=x—|xl
C.f(x)=x+1 D.f(x)= 一x
3.设函数y=f(x) 对任意正实数x,y 都有f(x·y)=
f(x)+f(y), 已知 f(8)=3, 则 f( √2)=
的定义域为R, 则 m 的取值 范围为
5.已知函数
(1)化简
(2)求
+f(4) 的值.
●
【加练·固】已知f(x)=2x+a,g(x)=
,若g(f(x))=x +x+1,
的值.
求 a
第三章 函数的概念与性质
3.1 函数的概念及其表示
3.1.1 函数的概念 第1课时 函数的概念
教师用书配套课性
定 义
设A,B是非空的实数集,如果对于集合A
中的任意一个数x,按照某种确定的对应关 系f,在集合B中都有唯一确定的数y和它 对应,那么就称f:A→B为从集合A到集合 B的一个函数
三 要 素 对应关系
y=f(x),x∈A
定义域
x的取值范围
值域
与x的值相对应的y的值的集合
f(x) ∈A}
基础自主学习
1.函数的概念
定义 名称 符号
数轴表示
闭区间
开区间 0
半开半 闭区间
半开半 闭区间
2.区间及有关概念
(1)一般区间的表示.
设a,b∈R, 且a
{x|x
符号 (a,十 (一
(—0 a)
(2)特殊区间的表示.
1.思维辨析(对的打“√”,错的打“×”)
(1)“y=f(x)”表示的是“y等于f 与x 的乘积”.( )
(2)根据函数的定义,定义域中的任何一个x 可以对应
着值域中不同的y. ( )
(3)在函数的定义中,集合B 是函数的值域. ( )
(4)在研究函数时,除用符号f(x) 外,还可用g(x),
F(x),G(x) 等来表示函数. ( )
素 养 小 测
提示:(1)×.f(x) 是一个符号,“y=f(x)” 是“y 是
函数”的数学表示.
(2) ×.根据函数的定义,对于定义域中的任何一个
值域中都有唯一的y 与之对应。
(3)×.在函数的定义中,函数的值域是集合B 的子集.
(4) √.同一个题中,为了区别不同的函数,常采用g(x), F(x),G(x) 等来表示函数.
则 f(3)=
3.用区间表示函数 的定义域是
类型一 函数关系的判断
【典例1】(1)设集合P={x|o≤x≤2},Q={ylo≤x≤2},
则图中能表示P 到 Q 的函数的是 ( )
① ② ③ ④
A.①②③④ B.①③④
C.①④ D.③
能力合作探究
②A={x|x>0,x∈R},B={yly∈R}, 对应关系f:x
→y =3x;
③A={x|x∈R},B={yly∈R}, 对应关系f:x→x 十
y =25;
④A=R,B=R, 对应关系f:x→y=x ;
⑤A={(x,y)|x∈R,y∈R},B=R, 对应关系f:(x,y)
→s=x 十y;
⑥A={x|—1≤x≤1,x∈R},B={0}, 对应关系f:x→
y=0.
A.①⑤⑥ B.②④⑤⑥
C.②③④ D.①②③⑤
(2)在下列从集合A 到集合B 的对应关系中,不能确定
y是x 的函数的是 ( )
①A={x|x∈Z},B={yly∈Z}, 对应关系f:x→y
【思维·引】
1.在x 轴上区间[0,2]内作与x 轴垂直的直线,此直线
与函数的图象恰有一个公共点.
2.先看集合A,B 是否为非空数集,再判断非空数集A
中任取一个数,在非空数集 B 中是否有唯一的数与之 对应.
【解析】(1)选C.根据函数的定义,在定义域内的任何一
个x 值,都唯一对应一个y 值,故①、④正确;②中定义 域内的1对应了2个函数值,③中定义域(1,2)内的x 值,没有对应的y 值,故②、③错误.
(2)选D.① 在对应关系f 下 ,A中不能被3整除的数在
B 中没有唯一确定的数与它对应,所以不能确定y 是x 的函数.②在对应关系f 下 ,A 中的数在B 中有两个数 与之对应,所以不能确定y 是x 的函数.③在对应关系 f 下,A 中的数(除去5与一5外)在B 中有两个数与之 对应,所以不能确定y 是 x 的函数.⑤A 不是数集,所 以不能确定y 是x 的 函 数 .④⑥显然满足函数的特征, y 是x 的函数.
两非空实数集A,B
一对一或多对一
A中不能有剩余元素
1.判断一个对应是否是函数的方法
类题 · 通
函数的
概念
作出
判断
2.根据图形判断对应是否为函数的步骤
(1)任做一条垂直于x 轴的直线l.
(2)在定义域内平行移动直线l.
(3)若l 与图形有且只有一个交点,则是函数;若在定义
域内没有交点或有两个或两个以上的交点,则不是函 数.如图所示:
不是函数图象
是函数图象
★习练·破
已知集合A={1,2,3,4},B={5,6,7}, 在下列A 到B 的
四种对应关系中,存在函数关系的个数是 ( )
① ② ③ ④
A.1 B.2 C.3 D.4
A B
A B
【解析】选B.根据函数的定义可知,集合A 中每一个实
数在B 中都有唯一确定的实数与之对应,其中①③均满 足函数的定义.
类型二 求函数的定义域
【典例2】(1)若将长为a 的铁丝折成矩形,则矩形面积 关
于一边长x 的解析式为 ,此函数的定义域 为
(2)求下列函数的定义域.
【思维·引】
(1)先用a 和x 表示另外一条边,然后根据两条边长都
大于0,列不等式组求定义域.
(2)①依据分式的分母不为0,列不等式求定义域。
②依据分式的分母不为0,二次根式的被开方数大于或
等于0,列不等式组求定义域.
【解析】(1)已知矩形的一边长为x, 则另一边长为
—2x),
,故定义域为
由 得
(2)①因为|x+1|≠0,x+1≠0,
所以定义域为{ x|x≠—1}.
所以定义域为{—1}.
所以x≠—1.
②因为
★ 类题·通
已知函数的解析式,求函数的定义域
(1)本质:求使得函数解析式有意义的自变量的取值
范围.
(2)常见题型:
①如果f( x) 是整式,那么函数的定义域是实数集R.
②如 果f(x) 是分式,那么函数的定义域是使分母不等于
零的实数的集合.
③如果f(x) 是二次根式,那么函数的定义域是使根号内
的式子大于或等于零的实数的集合.
④如果y=x°, 那么x≠0.
⑤如果f(x) 是由几个部分的数学式子构成的,那么函数
定义域是使各部分式子都有意义的实数集合(即求各部 分定义域的交集).
⑥对于由实际问题的背景确定的函数,其定义域还要受
实际问题的制约.
★习练·破
求下列函数的定义域:
;(2)y=√x- 1·√ 1—x;
;(4)
③
(1
得函数的定义域为
(2)由 →x=1, 得函数的定义域为{1}.
(3)由
得函数的定义域为{x|x≤1, 且x ≠0}.
(4)因为 ,解得x>—1, 且x≠1.
所以函数的定义域为{x|x>-1, 且x≠1}.
【解析】(1)由
●
的
【加练·固】
求下列函数的定义域.
得x>—2 且 x≠3.
所以所求函数的定义域为(—2,3)U(3, 十 ) .
(2)要使函数有意义,需满足
所以所求函数的定义域为(0,1) U(1, 十一).
【解析】(1)要使函数有意义,需满足
所以x>0 且 x≠1,
即
类型三 函数的对应关系的应用
角度1 求值问题
【典例3】(1)已知f(3x+1)=4x+3, 则 f(4)= ( )
A.6 B.7 C.8 D.9
(2)如图,函数f(x) 的图象是曲线OAB, 其中点O,A,B
的坐标分别为(0,0),(1,2),(3,1),则f(f(3)) 的值为
B
3 x
y
2
1
O
2
【思维·引】
1.注意到f(4)=f(3×1 +1) 就可以利用f(3x+1)=
4x+3 求f(4).
2.根据图象确定自变量x=1 和 x=3 时,对应的函数
值即可求f(f(3)).
【解析】(1)选B.由3x+1=4, 得x=1, 所以f(4)=f(3
×1+1)=4×1+3=7.
(2)据图象知,f(3)=1,f(f(3))=f(1)=2.
答案:2
①求f(3),f(4),f(g(3))及f(g(4))的值.
②求f(g(x)), 并证明f(x)+f(g(x)) 是常数.
角度2 求解析式问题
【典例4】已知函数
●
。
【解析
●
则
类题 · 通
函数求值的方法及关注点
(1)方法.
①求 f(a): 已 知f(x) 的解析式时,只需用a 替换解析式
中的x 即得f(a) 的值.
②求f(g(a)): 已 知f(x) 与 g(x), 求 f(g(a)) 的值应遵
循由里往外的原则.
(2)关注点:用来替换解析式中x 的 数a 必须是函数定
义域内的值,否则函数无意义.
习练 · 破
1.若f(x)=ax —√2,a
为正实数,且f(f(√2))=—√2, 则
a=
2.设f(x)=2x +2, ●
( 1 ) 求 f(2),f(a+3),g (a)+g(0)(a≠
—2),g(f(2)).
(2)求g(f(x)).
≠—2),
【加练·固】
若 (x≠—1), 求 f(0),f(1),
f(1—a)(a≠2),f(f(2)) 的值.
课堂达标检测
1.下列图形中,不能确定y 是x 的函数的是 ( )
y
3
x
B.
C. D.
3
A.
【解析】选D.任作一条垂直于x 轴的直线x=a, 移动直
线,根据函数的定义可知,此直线与函数图象至多有一 个交点.结合选项可知D 不满足要求,因此不表示函数 关系.
2.设函数f(x)=ax+b, 若f(1)=—2,f(—1)=0, 则
( )
A.a=1,b=— 1 B.a=— 1,b=— 1
C.a=—1,b=1 D.a=1,b=1
3.用区间表示数集{xlx≤2 或x>3} 为
,且 f(a)=2, 则 a=
若两个函数的对应关系相同,值域也相同,但定义域不
同,则称这两个函数为同族函数.那么与函数y=x ,x∈
{—1,0,1,2}为同族函数的个数有 ( )
A.5 个 B.6 个 C.7 个 D.8 个
新情境 · 新思维
【解析】选D. 由题意知同族函数是只有定义域不同的函
数,函数解析式为y=x , 值域为{0,1,4}时,定义域中,0 是肯定有的,正负1,至少含一个,正负2,至少含一个.它 的定义域可以是{0,1,2},{0,1,—2},{0,—1,2},{0, — 1,—2},{0,1,—2,2},{0,—1,—2,2},{0,1,—1, —2},{0,1,—1,2,—2},共有8种不同的情况,所以 D 选项是正确的.
函数的概念
基础练
一、选择题
1.设f:x→x 是集合A 到集合B 的函数,如果集合B=
{1},那么集合A 可能是 ( )
A.{1} B.{0}
C.{—1,1,0} D.{—1,0}
课时素养评价(十六)
A.(—1,2)U(2, 十○) B.(—1, 十 )
C.(—1,2) D.(—1, 十 )
2.函数 的定义域为
( )
【加练·固】已知集合A={x|x≥4},
的定义域为B, 若 A∩B=
,则实数a 的取值范围是 ( )
A.(—2,4) B.(3, 十 )
C. ( 一 , 3 ) D. ( 一 , 3 )
3.设M={x|o≤x≤2},N={ylo≤y≤2}, 给出以下四个
图形,其中能表示集合M 到集合N 的函数关系的有
( )
(1) (2) (3) (4)
A.0 个 B.1 个 C.2 个 D.3 个
【解析】选C.图象(1)中,集合M 内(1,2)的元素在集合
N 内没有对应元素,所以图象(1)不能表示集合M 到集 合N 的函数关系;图象(2)中,集合M 内的任意元素在 集合N 中都有唯一确定的对应元素,所以图象(2)能表 示集合M 到集合N 的函数关系;图象(3)中,集合M 内的任意元素在集合N 中都有唯一确定的对应元素, 所以图象(3)能表示集合M 到集合N 的函数关系;图 象(4)中,集合M 内的元素在集合N 中对应的元素不 唯一,所以图象(4)不能表示集合M 到集合N 的函数 关系.所以能表示集合M 到集合N 的函数关系的是 (2)、(3).
4.设f(x)=|x—1|—|x|,
B.0
则 等于
C.1
( )
A
口
【加练·固】已知函数 ,则
( )
B. C.a D.3a
A
二、填空题
5.(2a,3a—1) 为一确定的区间,则 a 的取值范围
是
6.已知函数 ,则g(x)=
,函数g(x) 的定义域是 .(用区间表
示 )
【加练·固】已知等腰△ABC 的周长为
10,底边长y 关于腰长x 的函数关系式为y=
10—2x,则此函数的定义域为
(1)求函数f(x) 的定义域;(2)求f(—1),f(12) 的值.
三 、解答题
能力练
1.给定的下列四个式子中,能确定y 是x 的函数的是
( )
A.x +y =1 B.|x—1|+√y -1=0
C.√x—1+√y-1=1 D.y=√x—3+√2—x
【解析】选C.A. 由x +y =1, 得y=± √1-x , 不满足
函数的定义,所以A 不是函数.B.由 |x—1|+√y -1=
0得, |x—1|=0,√y -1=0, 所以x=1,y=±1, 所以
B不是函数.C. 由√ x—1+√y-1 =1, 得 y=(1— √x—1) +1, 满足函数的定义,所以C 是函数.D. 要使 函数y=√x—3+ √2—x有意义,则 解得 此时不等式组无解,所以D 不是函数.
2.下列函数中,不满足f(2x)=2f(x) 的是 ( )
A.f(x)=|x| B.f(x)=x—|xl
C.f(x)=x+1 D.f(x)= 一x
3.设函数y=f(x) 对任意正实数x,y 都有f(x·y)=
f(x)+f(y), 已知 f(8)=3, 则 f( √2)=
的定义域为R, 则 m 的取值 范围为
5.已知函数
(1)化简
(2)求
+f(4) 的值.
●
【加练·固】已知f(x)=2x+a,g(x)=
,若g(f(x))=x +x+1,
的值.
求 a
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
