2.2 基本不等式课件(共40张PPT)- 高一上学期数学人教A版(2019)必修第一册
文档属性
| 名称 | 2.2 基本不等式课件(共40张PPT)- 高一上学期数学人教A版(2019)必修第一册 |
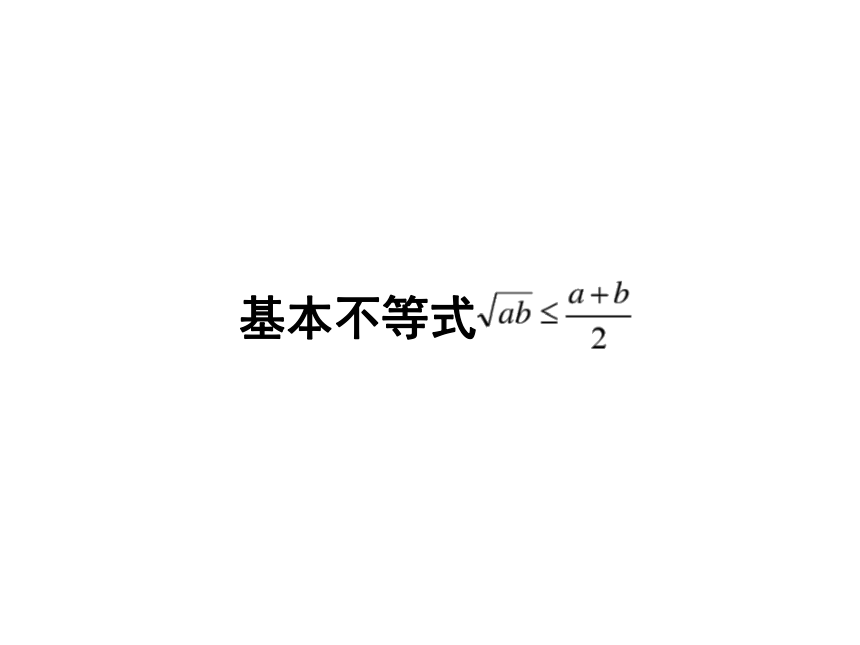
|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 15:29:40 | ||
图片预览
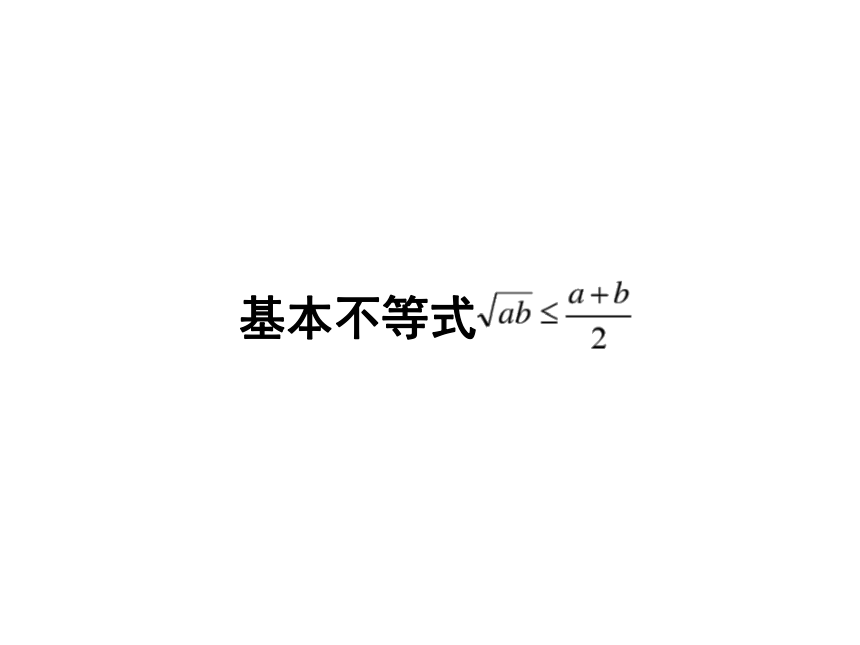










文档简介
(共40张PPT)
基本不等式
基本不等式的应用
基本不等式的推导及其证明
主要内容
第1课时
基本不等式的推导及其证明
探究
如图是在北京召开的第24界国
际数学家大会的会标,会标是根据 中国古代数学家赵爽的弦图设计的, 颜色的明暗使它看上去像一个风车, 代表中国人民热情好客.你能在这 个图案中找出一些相等关系或不等 关系吗
设直角三角形的两条直角边长为a、b,那么正方
形的边长为 √a +b ·
这样,4个直角三角形的面积的和是2ab, 正方
形的面积为a +b
将图中的“风车”抽象成如图,在正方形ABCD中
有4个全等的直角三角形.
由于4个直角三角形的面积小于正方形的面积,
我们就得到了一个不等式:
a +b ≥2ab
当直角三角形变为等腰直角三角形,即a=b 时,
正方形EFGH缩为一个点,这时有
a +b =2ab
证明:作差比较
a +b -2ab=(a-b)2
当a≠b时 ,(a-b) >0 得
a +b >2ab
当a=b时 ,(a-b) =0 得
a +b =2ab
所以对任意a,b∈R, 则a +b ≥2ab, 当且仅当a=b 时“=”成立.
若a,b∈R, 则a +b ≥2ab
时“=”成立).
(当且仅当a=b
结论1:
特别地,如果a>0,b>0,我们用 √a、 √b分别代替上 面结论中的a、b, 可得
贝
当且仅当a=b 时“=”成立
证明同前面结论1
结论2
若a>
探究 基本不等式 的几何意义
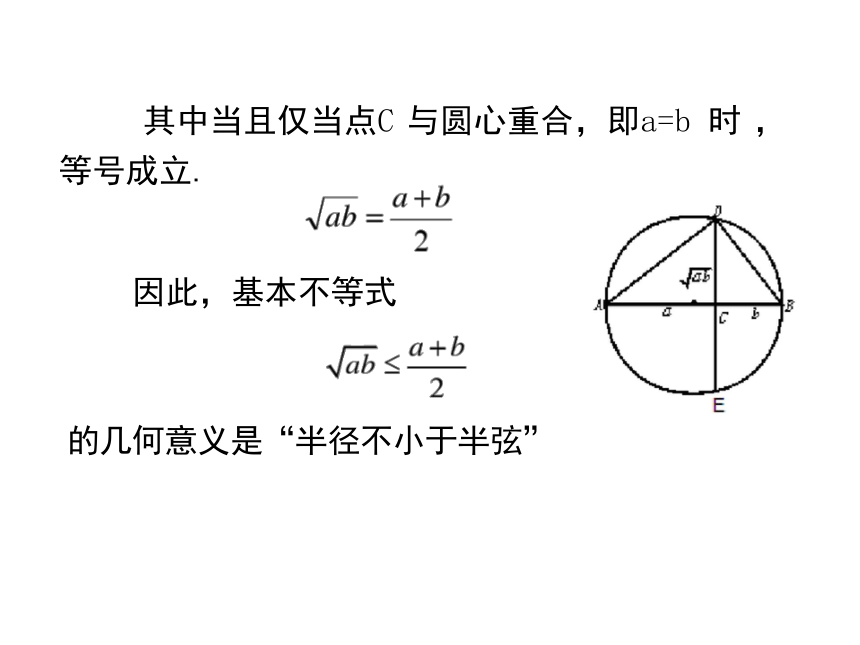
在右图中,AB是圆的直径,点C是AB上的一点,
AC=a,BC=b.过点C作垂直于AB的弦DE, 连接AD、BD. 你能利用这个图形得出基本不等式的几何解释吗
易证Rt△ACDo Rt△DCB,
即CD=√ab
由于CD不大于圆的半径
所以
那么 CD =CA·CB
其中当且仅当点C 与圆心重合,即a=b 时 ,
的几何意义是“半径不小于半弦”
因此,基本不等式
等号成立.
述为: 两个正数的等差中项不小于它们的等比中项.
为a 、b的算术平均数, √ab 为几何平均数,
那么
作是正数a 、b 的等差中项,把Jab
的等比中项,那么该定理可以叙
两个正数的算术平均数不小于它们的几何平均数.
如果
看作是正
基本不等式
代数意义
基本不等式的推广:
若a ,a2,…,an∈R+,则 叫做n
个正数的算术平均数,"a ·a …an 叫 做n个正数的
几何平均数.
n个正数的算术平均数不小于它们的几何平均数.
证明:(1)由于a∈R+, 事
当且仅当 即a=1时,等号成立.
事
(1)当a ∈R+时,
(2)当a,b∈R*时2
当且仅当 即a=b时,等号成立.
当a=b 时取“=”号)
例1 .求证
例2.已知x、y 都是正数,求证:
(x+y) (x +y ) (x +y )≥8x y .
证明:由于x、y都是正数,根据基本不等式得
x+y≥2Jxy>0
x +y ≥2xy>0
x +y ≥2√x y >0
三式相乘得
(x+y)(x +y )(x +y )≥8x y .
当且仅当x=y时等号成立.
∵x+y=2,
∴x +y ≥2
即x +y 的最小值为2,当且仅当x=y=1时取得最小值.
例3.若x>0,y>0, 且x+y=2, 求x +y 的最小值
解:∵x +y ≥2xy,
∴2(x +y )≥(x+y)
练习
(A)充分而非必要条件 (B)必要而非充分条件
(C)充要条件 (D)既非充分又非必要条件
2.甲、乙两车从A地沿同一路线到达B地,甲车一 半时间的速度为a, 另一半时间的速度为b; 乙车用速 度a行走了一半路程,用速度b行走了另一半路程,若 a≠b,则两车到达B地的情况是( A )
(A)甲车先到达B 地 (B)乙车先到达B地
(C)同时到达 (D)不能判定
1.“a>0 且b>0” 是 ”成立的(A )
(
3.已知a、b、c都是正数,求证
(a+b)(b+c)(c+a)≥8 abc
证明:由于a、b、c都是正数,根据基本不等式得
a+b≥2√ab>0
b+c≥2√bc>0
c+a≥2√ca>0
三式相乘得
(a+b) (b+c) (c+a)≥8 abc
当且仅当a=b=c 时等号成立.
(-a)+(-b)≥2√(-a)(-b)
a+b≤-2√ab
当且仅当-a=-b即a=b时等号成立.
4. 当 a,b∈R- 时,求证a+b≤-2√ab
证明:由a<0,b<0, 得 -a>0,-b>0
小结
1.基本不等式的推导及其意义
2.利用基本不等式证明简单不等式
作业
P100 练习1
P100 习题3.4 A组1,2
2.已知a 、b 、c>0, 求
3.求证:a +b +c ≥ab+bc+ca
补充作业
1.设a,b∈R+,且a≠b,则下列各式中正确的是( )
第2课时
基本不等式的应用
1.若a >2ab(当且仅当a=b 时“=”成立).
对于结论2,应把握三点: “一正、二定、三相等”
当且仅当a=b 时“=”成立
复习:基本不等式
2.若a、
, 贝
例1(1)用篱笆围成一个面积为100m 的矩形菜园,
问这个矩形的长、宽各为多少时,所用篱笆最短.最短 的篱笆是多少
(2)一段长为36 m的篱笆围成一个矩形菜园,问这
个矩形的长、宽各为多少时,菜园的面积最大,最大 面积是多少
分析:对于(1)矩形菜园的面积是确定的,长和宽没 有确定.篱笆最短即矩形的周长最短.
解:(1)设矩形菜园的长为x m,宽 为y m,则 xy=100, 篱笆的长为2(x+y)m. 由
当且仅当x=y时等号成立,此时x=y=10.
因此,这个矩形的长、宽都为10m时,所用的篱
笆最短,最短的篱笆是40m.
x+y≥2√ 100
2(x+y)≥40
可得
xy≤81
当且仅当x=y时,等号成立,此时x=y=9.
因此,这个矩形的长、宽都为9m时,菜园的面积
最大,最大面积是81m .
分析:对于(2)矩形菜园的周长是确定的,长和宽没
有确定.菜园的面积最大即矩形的面积最大.
解:(2)设矩形菜园的长为x m,宽为y m,则
2(x+y)=36,x+y=18, 矩形菜园的面积为xy m .由
可得
1. 已知两个正数x,y, 求x+y与xy的最值.
(1)xy为定值p, 那么当x=y 时,x+y有最小值2√p;
(2)x+y为定值s,那么当x=y 时,积xy有最大值
2.在使用“和为常数,积有最大值”和“积为常数,
和有最小值”这两个结论时,应把握三点: “一正、 二定、三相等”
利用基本不等式
求最值的要点
例2某工厂要建造一个长方体无盖贮水池,其
容积为4800m ,深为3m, 如果池底每1m 的造价为150 元,池壁每1m 的造价为120元,问怎样设计水池能 使总造价最低,最低总造价是多少元
分析:此题首先需要由实际问题向数学问题转
化,即建立函数关系式,然后求函数的最值,其中 用到了基本不等式定理.
=240000+720×2×40=297600
当 即x=40 时,z有最小值2976000.
因此,当水池的底面是边长为40m的正方形时,
水池的总造价最低,最低总造价是297600元.
解:设水池底面一边的长度为x
价为z元,根据题意,得
m,水池的总造
例3.已知x>1,求x 的最小值以及取得最小
值 时x 的 值 .
解:因为 x>1 所以 x—1>0
当且仅当 (x>1)即x=2时,取“=”号.
答:最小值是3,取得最小值时x的值为2.
例4已知 x,y∈R+,a、b为正常数,且 求x+y的最小值.
解1
≥2√ab+a+b=(Ja+√b)
例5.求函数 的最小值.
分析:利用函数 (t>0) 的单调性.
t∈(0,1)单调递减,t∈[1,+00)单调递增
令t= √x +4 贝
∴当t=2,即:x=0 时,
(t≥2)
练习
1. 下列函数中,最小值为4的是( C )
4
(C)y=4e^+e
D)y=log x+log 3(02.某公司租地建仓库,每月土地占用费y 与仓库到
车站的距离成反比,而每月库存货物的运费y 与到车 站的距离成正比,如果在距离车站10公里处建仓库, 这两项费用y 和y 分别为2万元和8万元,那么要使这两 项费用之和最小,仓库应建在离车站( A )
(A)5公里 (B)4公里 (C)3公里 (D)2公里
3.已知lgx+lgy=1, 的最小值是
4.若正数x 、y 满足x+2y=1. 求 的最小值.
5.已知正数a 、b 满足a+b=1.
(1)求ab的取值范围;(2)求 的最小值.
∵X>-1.∴X+1>0 又 ∵
当且仅当 即x=√5-1 时取“=”号 即当x=√5-1 时,函数的最小值为2 √5-5
的最小值.
6.求函数
7.如图,为处理含有某种杂质的矿水,要制造
一底宽为2米的无盖长方形沉淀箱,污水从A 孔流 入,经沉淀后从B孔流出,设箱体的长度为a米,高 度为b米,已知流出的水中该杂质的质量分数与a, b的乘积ab 成反比.现有制箱材料60平方米,问当 a,b 各为多少米时,经沉淀后流出的水中该杂质的 质量分数最小(A,B 孔的面积忽略不计).
小结
1. 已知两个正数x,y, 求x+y与xy 的最值.
(1)xy为定值p,那么当x=y 时,x+y有最小值2√p;
(2)x+y 为定值s, 那么当x=y 时,积xy有最大值
2.在使用“和为常数,积有最大值”和“积为常数,
和有最小值”这两个结论时,应把握三点: “一正、 二定、三相等”
3.利用基本不等式求函数最值的步骤:
①各项必须为正;
②含变数的各项和或积必须为定值;
③必须有自变量值能使函数取到等号.
一正,二定,三相等
作业
习题P100-101.A 组,2,3,4B 组1,2
基本不等式
基本不等式的应用
基本不等式的推导及其证明
主要内容
第1课时
基本不等式的推导及其证明
探究
如图是在北京召开的第24界国
际数学家大会的会标,会标是根据 中国古代数学家赵爽的弦图设计的, 颜色的明暗使它看上去像一个风车, 代表中国人民热情好客.你能在这 个图案中找出一些相等关系或不等 关系吗
设直角三角形的两条直角边长为a、b,那么正方
形的边长为 √a +b ·
这样,4个直角三角形的面积的和是2ab, 正方
形的面积为a +b
将图中的“风车”抽象成如图,在正方形ABCD中
有4个全等的直角三角形.
由于4个直角三角形的面积小于正方形的面积,
我们就得到了一个不等式:
a +b ≥2ab
当直角三角形变为等腰直角三角形,即a=b 时,
正方形EFGH缩为一个点,这时有
a +b =2ab
证明:作差比较
a +b -2ab=(a-b)2
当a≠b时 ,(a-b) >0 得
a +b >2ab
当a=b时 ,(a-b) =0 得
a +b =2ab
所以对任意a,b∈R, 则a +b ≥2ab, 当且仅当a=b 时“=”成立.
若a,b∈R, 则a +b ≥2ab
时“=”成立).
(当且仅当a=b
结论1:
特别地,如果a>0,b>0,我们用 √a、 √b分别代替上 面结论中的a、b, 可得
贝
当且仅当a=b 时“=”成立
证明同前面结论1
结论2
若a>
探究 基本不等式 的几何意义
在右图中,AB是圆的直径,点C是AB上的一点,
AC=a,BC=b.过点C作垂直于AB的弦DE, 连接AD、BD. 你能利用这个图形得出基本不等式的几何解释吗
易证Rt△ACDo Rt△DCB,
即CD=√ab
由于CD不大于圆的半径
所以
那么 CD =CA·CB
其中当且仅当点C 与圆心重合,即a=b 时 ,
的几何意义是“半径不小于半弦”
因此,基本不等式
等号成立.
述为: 两个正数的等差中项不小于它们的等比中项.
为a 、b的算术平均数, √ab 为几何平均数,
那么
作是正数a 、b 的等差中项,把Jab
的等比中项,那么该定理可以叙
两个正数的算术平均数不小于它们的几何平均数.
如果
看作是正
基本不等式
代数意义
基本不等式的推广:
若a ,a2,…,an∈R+,则 叫做n
个正数的算术平均数,"a ·a …an 叫 做n个正数的
几何平均数.
n个正数的算术平均数不小于它们的几何平均数.
证明:(1)由于a∈R+, 事
当且仅当 即a=1时,等号成立.
事
(1)当a ∈R+时,
(2)当a,b∈R*时2
当且仅当 即a=b时,等号成立.
当a=b 时取“=”号)
例1 .求证
例2.已知x、y 都是正数,求证:
(x+y) (x +y ) (x +y )≥8x y .
证明:由于x、y都是正数,根据基本不等式得
x+y≥2Jxy>0
x +y ≥2xy>0
x +y ≥2√x y >0
三式相乘得
(x+y)(x +y )(x +y )≥8x y .
当且仅当x=y时等号成立.
∵x+y=2,
∴x +y ≥2
即x +y 的最小值为2,当且仅当x=y=1时取得最小值.
例3.若x>0,y>0, 且x+y=2, 求x +y 的最小值
解:∵x +y ≥2xy,
∴2(x +y )≥(x+y)
练习
(A)充分而非必要条件 (B)必要而非充分条件
(C)充要条件 (D)既非充分又非必要条件
2.甲、乙两车从A地沿同一路线到达B地,甲车一 半时间的速度为a, 另一半时间的速度为b; 乙车用速 度a行走了一半路程,用速度b行走了另一半路程,若 a≠b,则两车到达B地的情况是( A )
(A)甲车先到达B 地 (B)乙车先到达B地
(C)同时到达 (D)不能判定
1.“a>0 且b>0” 是 ”成立的(A )
(
3.已知a、b、c都是正数,求证
(a+b)(b+c)(c+a)≥8 abc
证明:由于a、b、c都是正数,根据基本不等式得
a+b≥2√ab>0
b+c≥2√bc>0
c+a≥2√ca>0
三式相乘得
(a+b) (b+c) (c+a)≥8 abc
当且仅当a=b=c 时等号成立.
(-a)+(-b)≥2√(-a)(-b)
a+b≤-2√ab
当且仅当-a=-b即a=b时等号成立.
4. 当 a,b∈R- 时,求证a+b≤-2√ab
证明:由a<0,b<0, 得 -a>0,-b>0
小结
1.基本不等式的推导及其意义
2.利用基本不等式证明简单不等式
作业
P100 练习1
P100 习题3.4 A组1,2
2.已知a 、b 、c>0, 求
3.求证:a +b +c ≥ab+bc+ca
补充作业
1.设a,b∈R+,且a≠b,则下列各式中正确的是( )
第2课时
基本不等式的应用
1.若a >2ab(当且仅当a=b 时“=”成立).
对于结论2,应把握三点: “一正、二定、三相等”
当且仅当a=b 时“=”成立
复习:基本不等式
2.若a、
, 贝
例1(1)用篱笆围成一个面积为100m 的矩形菜园,
问这个矩形的长、宽各为多少时,所用篱笆最短.最短 的篱笆是多少
(2)一段长为36 m的篱笆围成一个矩形菜园,问这
个矩形的长、宽各为多少时,菜园的面积最大,最大 面积是多少
分析:对于(1)矩形菜园的面积是确定的,长和宽没 有确定.篱笆最短即矩形的周长最短.
解:(1)设矩形菜园的长为x m,宽 为y m,则 xy=100, 篱笆的长为2(x+y)m. 由
当且仅当x=y时等号成立,此时x=y=10.
因此,这个矩形的长、宽都为10m时,所用的篱
笆最短,最短的篱笆是40m.
x+y≥2√ 100
2(x+y)≥40
可得
xy≤81
当且仅当x=y时,等号成立,此时x=y=9.
因此,这个矩形的长、宽都为9m时,菜园的面积
最大,最大面积是81m .
分析:对于(2)矩形菜园的周长是确定的,长和宽没
有确定.菜园的面积最大即矩形的面积最大.
解:(2)设矩形菜园的长为x m,宽为y m,则
2(x+y)=36,x+y=18, 矩形菜园的面积为xy m .由
可得
1. 已知两个正数x,y, 求x+y与xy的最值.
(1)xy为定值p, 那么当x=y 时,x+y有最小值2√p;
(2)x+y为定值s,那么当x=y 时,积xy有最大值
2.在使用“和为常数,积有最大值”和“积为常数,
和有最小值”这两个结论时,应把握三点: “一正、 二定、三相等”
利用基本不等式
求最值的要点
例2某工厂要建造一个长方体无盖贮水池,其
容积为4800m ,深为3m, 如果池底每1m 的造价为150 元,池壁每1m 的造价为120元,问怎样设计水池能 使总造价最低,最低总造价是多少元
分析:此题首先需要由实际问题向数学问题转
化,即建立函数关系式,然后求函数的最值,其中 用到了基本不等式定理.
=240000+720×2×40=297600
当 即x=40 时,z有最小值2976000.
因此,当水池的底面是边长为40m的正方形时,
水池的总造价最低,最低总造价是297600元.
解:设水池底面一边的长度为x
价为z元,根据题意,得
m,水池的总造
例3.已知x>1,求x 的最小值以及取得最小
值 时x 的 值 .
解:因为 x>1 所以 x—1>0
当且仅当 (x>1)即x=2时,取“=”号.
答:最小值是3,取得最小值时x的值为2.
例4已知 x,y∈R+,a、b为正常数,且 求x+y的最小值.
解1
≥2√ab+a+b=(Ja+√b)
例5.求函数 的最小值.
分析:利用函数 (t>0) 的单调性.
t∈(0,1)单调递减,t∈[1,+00)单调递增
令t= √x +4 贝
∴当t=2,即:x=0 时,
(t≥2)
练习
1. 下列函数中,最小值为4的是( C )
4
(C)y=4e^+e
D)y=log x+log 3(0
车站的距离成反比,而每月库存货物的运费y 与到车 站的距离成正比,如果在距离车站10公里处建仓库, 这两项费用y 和y 分别为2万元和8万元,那么要使这两 项费用之和最小,仓库应建在离车站( A )
(A)5公里 (B)4公里 (C)3公里 (D)2公里
3.已知lgx+lgy=1, 的最小值是
4.若正数x 、y 满足x+2y=1. 求 的最小值.
5.已知正数a 、b 满足a+b=1.
(1)求ab的取值范围;(2)求 的最小值.
∵X>-1.∴X+1>0 又 ∵
当且仅当 即x=√5-1 时取“=”号 即当x=√5-1 时,函数的最小值为2 √5-5
的最小值.
6.求函数
7.如图,为处理含有某种杂质的矿水,要制造
一底宽为2米的无盖长方形沉淀箱,污水从A 孔流 入,经沉淀后从B孔流出,设箱体的长度为a米,高 度为b米,已知流出的水中该杂质的质量分数与a, b的乘积ab 成反比.现有制箱材料60平方米,问当 a,b 各为多少米时,经沉淀后流出的水中该杂质的 质量分数最小(A,B 孔的面积忽略不计).
小结
1. 已知两个正数x,y, 求x+y与xy 的最值.
(1)xy为定值p,那么当x=y 时,x+y有最小值2√p;
(2)x+y 为定值s, 那么当x=y 时,积xy有最大值
2.在使用“和为常数,积有最大值”和“积为常数,
和有最小值”这两个结论时,应把握三点: “一正、 二定、三相等”
3.利用基本不等式求函数最值的步骤:
①各项必须为正;
②含变数的各项和或积必须为定值;
③必须有自变量值能使函数取到等号.
一正,二定,三相等
作业
习题P100-101.A 组,2,3,4B 组1,2
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
