集合间的基本关系【新教材】人教A版高中数学必修第一册课件(共48张PPT)
文档属性
| 名称 | 集合间的基本关系【新教材】人教A版高中数学必修第一册课件(共48张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 774.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 00:00:00 | ||
图片预览










文档简介
(共48张PPT)
第一章
集合与常用逻辑用语
1.2 集合间的基本关系
· 【素养目标】
·1.理解集合之间包含和相等的含义,并会用符号和Venn图表示.(直观想 象)
·2.会识别给定集合的真子集,会判断给定集合间的关系,并会用符号 和Venn图表示.(直观想象)
·3.在具体情境中理解空集的含义.(数学抽象)
· 【学法解读】
·1.在本节学习中,学生要以义务教育阶段学过的数学内容为载体,依 据老师创设合适的问题情境,理解子集、真子集、集合相等、空集等概
今
心
·2.要注意集合之间关系的几种表述方法:自然语言、符合语言、图形 语言,应理解并掌握以上方法的转化及应用.
目 录 CONTENTS
必备知识·探新知
关键能力·攻重难
课堂检测·固双基
素养作业·提技能
必备知识·探新知
定义
一般地,对于两个集合A,B,如果集合A中 元素都是集合B中的晃素,就称集
合A为集合B的子集
记法与读法
ACB B2A
记作 ( 或 ),读作“A包含于B”(或“B包含A”)
基础知识
知识点1 子集、真子集的概念
·1.子集的概念
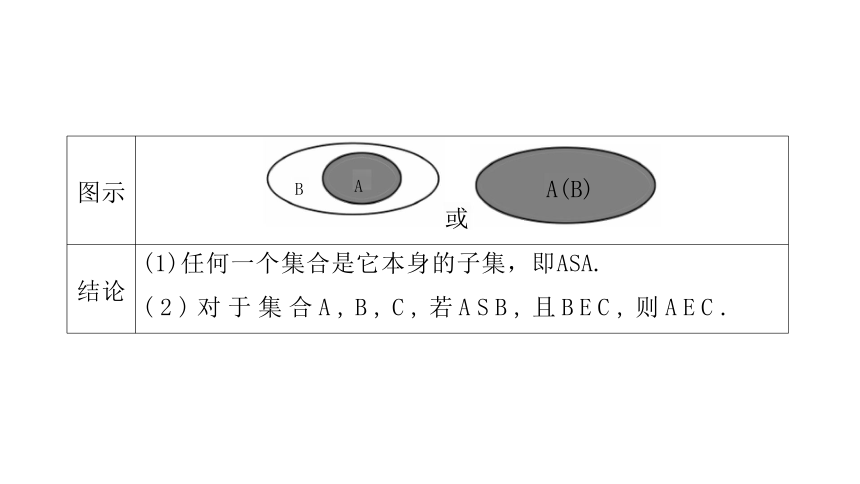
图示 B A 或
A(B)
结论 (1)任何一个集合是它本身的子集,即ASA. ( 2 ) 对 于 集 合 A , B , C , 若 A S B , 且 B E C , 则 A E C .
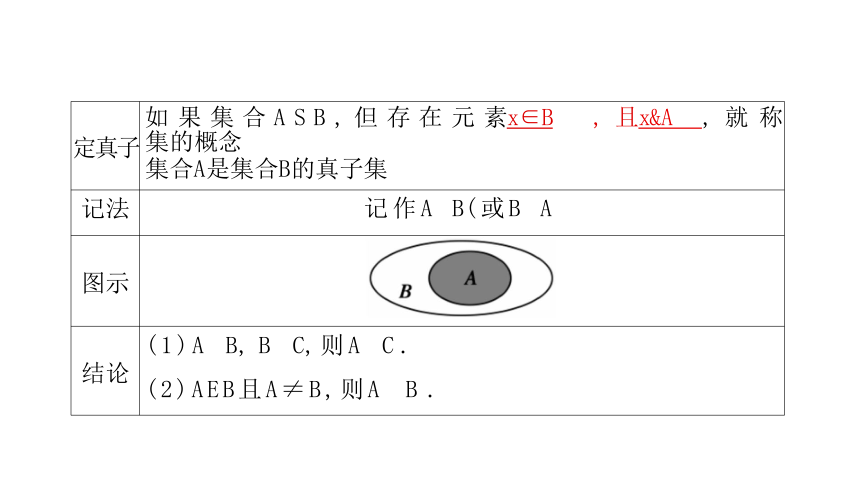
定真子
如 果 集 合 A S B , 但 存 在 元 素x∈B , 且x&A , 就 称
集的概念
集合A是集合B的真子集
记法
记作A B(或B A
图示
结论
(1)A B, B C,则A C .
(2)AEB且A≠B,则A B .
·思考1:(1)任意两个集合之间是否有包含关系
·(2)符合“∈”与 “C” 有什么区别
·提示:(1)不一定,如集合A={1,3},B={2,3},这两个集合就没有包含关
系 .
·(2)①“∈”是表示元素与集合之间的关系,比如1∈N,-1∈N.
·②“≤”是表示集合与集合之间的关系,比如NER,{1,2,3}={3,2,1}.
·③“∈”的左边是元素,右边是集合,则“三”的两边均为集合.
自然语言
如果集合A的任何一个元素都是集合B的元素,同时
集合B的任何一个元素,都是集合A的元素,那么集
合A与集合B相等,记作A=B.
符号语言
A C B 且 B A A = B
图形语言
B(A)
知识点2
集合相等
·思考2:怎样证明或判断两个集合相等
·提示:(1)若ASB且BSA, 则A=B, 这就给出了证明两个集合相等的方法, 即欲证A=B, 只需证ACB 与BEA 均成立 .
·(2)判断两个集合相等,可把握两个原则:①设两集合A,B 均为有限集, 若两集合的元素个数相同,对应元素分别相同,则两集合相等,即A=B; ②设两集合A,B 均是无限集,只需看两集合的代表元素满足的条件是 否一致,若一致,则两集合相等,即A=B.
定义
不含任何元素的集合叫做空集
记法
规定
空集是任何集合的子集,即oCA
特性
(1)空集只有一个子集,即它的本身,2
, 则)A
知识点3
空集
与0
相同点 都表示无的意思 都是集合
都是集合
不同点 0是集合;0是实数 0不含任何元素; {0}含一个元素0
0不含任何元素;
一个元素,该元素是
关系 0
· 思考3:0,0,{0}与{0}之间有怎样的关系
·提示:
Venn图
● 在数学中,经常用平面 上 的内部代表集合,这种图称为 Venn图,这种表示集合的方法叫做图票法.
·注意:1.用Venn图可以直观、形象地表示出集合之间的关系
2.Venn 图适用于元素个数较少的集合. ·思考4: Venn图的优点是什么
·提示:形象直观 .
ACB
BEA
1. 已知集合M={1},N={1,2,3}, 则有( D )
A.MC.NCM D.M N
[解析] ∵1∈{1,2,3},∴{1}{1,2,3}.故选D.
基础自测
·2.下列四个集合中,是空集的为(
·A.{0} B.{x|x>8, 且x<5}
·C.{x∈N|x —1=0} D.{x|x>4}
·[解析] x>8, 且x<5的数x不存在,∴选项B 中的集合不含有任何元素, 故选B.
·3.用适当的符号填空:
·(1)a {a,b,c};(2)0 {x|x =0};(3)Q {x∈R|x +1=0}; (4){0,1} N;(5){0} {x|x=x};(6){2,1} {xTx —3x+2=
0}.
·4.写出集合{a,b,c} 的所有子集.
· [解析]0,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}.
5. 判断下列两个集合之间的关系:
(1)A={x|x<0},B={x|x<1};
(2)A={x|x=3k,k∈N},B={x|x=6z,z∈N};
(3)A={x∈N+|x是4与10的公倍数},B={x|x=20m,m∈N+}.
[解析] (1)A B (2)A B (3)A=B
关键能力·攻重难
题型一集合间关系的判断
例 1(2020·石家庄高一教学质检)指出下列各组集合之间的关系:
(1)A={x|-1(2)A={x|x=2n,n∈Z},B={x|x=4n,n∈Z};
(3)A={x|x —x=0}, ,n∈Z};
(4)A={(x,y)|xy>0},B={(x,y)x>0,y>0 或x<0,y<0};
(5)A={xx=1+a ,a∈N+},B={x|x=a —4a+5,a∈N+}.
题型探究
·[分析] (1)中集合表示不等式,可以根据范围直接判断,也可以利用数 轴判断;(2)根据集合表示数集的意义进行判断;(3)解集合A中方程得到 集合A, 再根据集合B中n分别为奇数、偶数得到集合B, 进行判断;(4) 可以根据集合中元素的特征或者集合的几何意义判断;(5)将集合A中x关 于a的关系式改写成集合B中的形式,再进行判断.
[解析] (1)方法一集合B 中的元素都在集合A 中,但集合A 中有
些元素(比如0,—0.5)不在集合B 中,故B A.
方法二 利用数轴表示集合A,B, 如图所示,由图可知 B A.
(2)∵集合A 是偶数集,集合B 是4的倍数集,∴B A.
(3)A={x|x —x=0}={0,1}.在集合B中,当n 为奇数时,
= 0 , 当n 为偶数时, , ∴B={0,1},∴A=B.
(4)方法一 由 xy>0 得 x>0,y>0 或 x<0,y<0; 由 x>0,y>0 或 x<0,
y<0 得 xy>0, 从 而A=B.
方法二 集 合A 中的元素是平面直角坐标系中第一、三象限内的点
对应的坐标,集合 B 中的元素也是平面直角坐标系中第一、三象限内的 点对应的坐标,从而A=B.
(5)对于任意x ∈A, 有x=1+a =(a+2) -4(a+2)+5.
a∈N+, ∴a+2∈N+,∴x∈B.
由子集的定义知,ASB,
设1∈B, 此时a —4a+5=1, 解得a=2,a∈N+
∵1+a =1 在 a ∈N+时无解,∴14A.
综上所述,A B.
·[归纳提升]判断集合间关系的常用方法
·(1)列举观察法
·当集合中元素较少时,可列出集合中的全部元素,通过定义得出集合之 间的关系.
·(2)集合元素特征法
·首先确定集合的代表元素是什么,弄清集合元素的特征,再利用集合元 素的特征判断关系
·一般地,设A={x|p(x)},B={x|q(x)},①若 由p(x)可推出q(x),则ASB; ②若由q(x)可推出p(x), 则BCA;③ 若p(x),q(x) 可互相推出,则A=B;④ 若由p(x)推不出q(x), 由 q(x)也推不出p(x), 则集合A,B 无包含关系.
·(3)数形结合法
·利用Venn图、数轴等直观地判断集合间的关系.一般地,判断不等式的 解集之间的关系,适合画出数轴
· 【对点练习】①(2020·四川广元外国语高一段考)下列各式中,正确的 个数是( )
·①0={0};D②0S{0};③O∈{0};④0={0};⑤0∈{0};⑥{1}∈{1,2,3};⑦
{1,2}S{1,2,3};⑧{a,b}S{b,a}.
·A.1 B.2
·C.3 D.4
·[解析]0表示空集,没有元素_ {0}有一个元素,则o≠{0},故①错误; ∵空集是任何集合的子集,故②正确;O和{0}都表示集合,故③错误; 0表示元素,{0}表示集合,故④错误;O∈{0},故⑤正确;{1},{1,2,3} 都表示集合,故⑥错误;{1,2}中的元素都是{1,2,3}中的元素,故⑦正确; 由于集合的元素具有无序性,故{a,b}S{b,a}, 故⑧正确.综上,正
确的个数是4个.
题型二确定集合的子集、真子集
设A={x|(x —16)(x +5x+4) =0}, 写出集合A的子集,并指
[分析] 用列举法表示集合A
从子集中除去集合
A本身即得真子集
根据子集中所含元 素的个数写出子集
出其T 哪兰是它的真子集.
·[解析] 由(x -16)(x +5x+4)=0, 得(x-4)(x+1)(x+4) =0, 则方程的 根为x=-4 或x=-1 或x=4.
·故集合A={-4,-1,4}, 由0个元素构成的子集为:0.
·由1个元素构成的子集为:{-4},{-1},{4}.
·由2个元素构成的子集为:{-4,-1},{-4,4},{-1,4}.
·由3个元素构成的子集为:{-4,-1,4}.
·因此集合A的子集为:0,{-4},{-1},{4},{-4,-1},{-4,4},{- 1,4},{-4,-1,4}.
·真子集为:0,{-4},{-1},{4},{-4,-1},{-4,4},{-1,4}.
·[归纳提升](1)若集合A中有n(n∈N+)个元素,则集合A有2n个子集,有 (2n-1) 个真子集,有(2n-1) 个非空子集,有(2n-2) 个非空真子集.
·(2)写出一个集合的所有子集时,首先要注意两个特殊的子集:0和自
身.其次,依次按含有1个元素的子集,含有2个元素的子集,含有3个 元素的子集……——写出,保证不重不漏.
A.2 B.6
C.7 D.8
·[解析]由题意知,集合A可以为{a,b},{a,b,c},{a,b,d},{a,b, e},{a,b,c,d},{a,b,c,e},{a,b,d ,e}.
【对点练习】②满足{a,b}EA {a,b,c,d,e}的集合A 的个数
是(C)
题型三 由集合间的关系求参数范围问题
例 3 已知集合A={x|-3≤x≤4},B={x|2m—1BSA. 水头数m的取值范围.
·[分析]借助数轴分析,注意B是否为空集.
·[解析] (1)因为BCA,
· 当B=0 时 ,m+1≤2m-1, 解 得m≥2.
(2)当B≠0 时,有
解得— 1≤m<2, 综上得m≥—1.
·[归纳提升](1)分析集合间的关系时,首先要分析、简化每个集合.(2) 借助数轴,利用数轴分析法,将各个集合在数轴上表示出来,以形定数, 还要注意验证端点值,做到准确无误, 一般含“=”用实心点表示,不 含“=”用空心点表示.
·此类问题要注意对空集的讨论.
·【对点练习】③(1)已知集合A={— 1,3,2m—1},集合 若
BGA, 则 实 数m= ;
·(2)已知集合A={x|x<-1, 或x>4},B={x|2a≤x≤a+3}, 若BSA, 求实数a 的取值范围.
·[解析](1)因为BSA, 所以m =2m-1,
·即(m-1) =0, 所以m=1.当m=1 时 ,A={-1,3,1},B={3,1}, 满足BCA, 故m=1.
(2)当B=0 时,只需2a>a+3, 即 a>3;
当B≠o 时,根据题意作出如图所示的数轴,
-1 4 2a a+3 X
2a a+3 -1 4 X
综上可得,实数a 的取值范围为a<—4 或 a>2.
, 解 得a<—4 或 2可
已知集合A={—1,1},B={x|ax+1
所 例 4(值的集合为( )
·A.{—1} B.{1} D
·C.{—1,1}D.{—1,0,1}
因此有 所 以a=±1,
[错解] 因为 而
=0}, 若 BSA, 则 实 数 的
· 忽视“空集”的存在
误区警示
故 选C.
[错因分析] 空集是一个特殊而重要的集合,它不含任何元素,记为
0.在解隐含有空集参与的集合问题时,极易忽视空集的特殊性而导致错 解.本例求解过程中有两处错误, 一是方程ax=—1 的解不能写成x= 一
,二是忽视了BSA 时 ,B 可以为空集 .事实上a=0 时,方程无解.
[正解] 因为BSA, 所以当B≠a,即a≠0时 , 因
此有 所以a=±1; 当 B=0, 即 a=0 时满足条件.
综上可得实数a 的所有可能取值的集合是{—1,0,1}.故选D.
·[方法点拨]已知两个集合之间的关系求参数时,要根据集合间的关系 来确定元素之间的关系,需关注子集是否为空集.
·一般地,当集合为有限集时,往往通过列方程或方程组来处理,此时需 注意集合中元素的互异性;当集合为连续型无限集时,往往借助数轴列 不等式或不等式组来求解,要注意运用分类讨论、数形结合等思想方法, 尤其需注意端点值能否取到.
·分类讨论思想的应用
·分类讨论,通俗地讲,就是“化整为零,各个击破”.分类讨论要弄清 楚是依据哪个参数进行分类的,采用的标准是什么.分类讨论的原则是: (1)不重不漏;(2)一次分类只能按所确定的同一个标准进行.
学科素养
+1)=0,
当 a=0 时,集合B 中的三个元素相同,不满足集合中元素的互异性,
故a≠0,c —2c+1=0, 即 c=1.
当c=1 时,集合B 中的三个元素也相同,∴c=1 舍去,即此时无解.
·[分析] 根据集合相等的定义和集合元素的互异性求解.由于A=B, 元 素a 在两个集合中都有,故其余两个元素的情况需分类讨论.
消去b 得a+ac —2ac=0, 即 a(c —2c
已知集合A={a,a+b,a+2b},B={a,ac,ac },
[解析] ①
若A=B,
例 5
且
求 C
②若 消去b 得 2ac —ac—a=0,
即a(2c —c—1)=0,∵a≠0,∴2c —c—1=0,
∴A=B. 综上可知
即(c-1)(2c+1)=0. 又∵c≠1,∴
当 时
,
·[归纳提升] 1.两个集合相等,则所含元素完全相同,与顺序无关,但 要注意检验,排除与集合元素互异性或与已知相矛盾的情形.
·2.若两个集合中元素均为无限多个,要看两集合的代表元素是否一致, 且看代表元素满足条件是否一致,若均一致,则两集合相等.
课堂检测·固双基
点击进入WORD
文档
素养作业·提技能
点击进入WORD
文档
演示完毕
谢谢欣赏
第一章
集合与常用逻辑用语
1.2 集合间的基本关系
· 【素养目标】
·1.理解集合之间包含和相等的含义,并会用符号和Venn图表示.(直观想 象)
·2.会识别给定集合的真子集,会判断给定集合间的关系,并会用符号 和Venn图表示.(直观想象)
·3.在具体情境中理解空集的含义.(数学抽象)
· 【学法解读】
·1.在本节学习中,学生要以义务教育阶段学过的数学内容为载体,依 据老师创设合适的问题情境,理解子集、真子集、集合相等、空集等概
今
心
·2.要注意集合之间关系的几种表述方法:自然语言、符合语言、图形 语言,应理解并掌握以上方法的转化及应用.
目 录 CONTENTS
必备知识·探新知
关键能力·攻重难
课堂检测·固双基
素养作业·提技能
必备知识·探新知
定义
一般地,对于两个集合A,B,如果集合A中 元素都是集合B中的晃素,就称集
合A为集合B的子集
记法与读法
ACB B2A
记作 ( 或 ),读作“A包含于B”(或“B包含A”)
基础知识
知识点1 子集、真子集的概念
·1.子集的概念
图示 B A 或
A(B)
结论 (1)任何一个集合是它本身的子集,即ASA. ( 2 ) 对 于 集 合 A , B , C , 若 A S B , 且 B E C , 则 A E C .
定真子
如 果 集 合 A S B , 但 存 在 元 素x∈B , 且x&A , 就 称
集的概念
集合A是集合B的真子集
记法
记作A B(或B A
图示
结论
(1)A B, B C,则A C .
(2)AEB且A≠B,则A B .
·思考1:(1)任意两个集合之间是否有包含关系
·(2)符合“∈”与 “C” 有什么区别
·提示:(1)不一定,如集合A={1,3},B={2,3},这两个集合就没有包含关
系 .
·(2)①“∈”是表示元素与集合之间的关系,比如1∈N,-1∈N.
·②“≤”是表示集合与集合之间的关系,比如NER,{1,2,3}={3,2,1}.
·③“∈”的左边是元素,右边是集合,则“三”的两边均为集合.
自然语言
如果集合A的任何一个元素都是集合B的元素,同时
集合B的任何一个元素,都是集合A的元素,那么集
合A与集合B相等,记作A=B.
符号语言
A C B 且 B A A = B
图形语言
B(A)
知识点2
集合相等
·思考2:怎样证明或判断两个集合相等
·提示:(1)若ASB且BSA, 则A=B, 这就给出了证明两个集合相等的方法, 即欲证A=B, 只需证ACB 与BEA 均成立 .
·(2)判断两个集合相等,可把握两个原则:①设两集合A,B 均为有限集, 若两集合的元素个数相同,对应元素分别相同,则两集合相等,即A=B; ②设两集合A,B 均是无限集,只需看两集合的代表元素满足的条件是 否一致,若一致,则两集合相等,即A=B.
定义
不含任何元素的集合叫做空集
记法
规定
空集是任何集合的子集,即oCA
特性
(1)空集只有一个子集,即它的本身,2
, 则)A
知识点3
空集
与0
相同点 都表示无的意思 都是集合
都是集合
不同点 0是集合;0是实数 0不含任何元素; {0}含一个元素0
0不含任何元素;
一个元素,该元素是
关系 0
· 思考3:0,0,{0}与{0}之间有怎样的关系
·提示:
Venn图
● 在数学中,经常用平面 上 的内部代表集合,这种图称为 Venn图,这种表示集合的方法叫做图票法.
·注意:1.用Venn图可以直观、形象地表示出集合之间的关系
2.Venn 图适用于元素个数较少的集合. ·思考4: Venn图的优点是什么
·提示:形象直观 .
ACB
BEA
1. 已知集合M={1},N={1,2,3}, 则有( D )
A.M
[解析] ∵1∈{1,2,3},∴{1}{1,2,3}.故选D.
基础自测
·2.下列四个集合中,是空集的为(
·A.{0} B.{x|x>8, 且x<5}
·C.{x∈N|x —1=0} D.{x|x>4}
·[解析] x>8, 且x<5的数x不存在,∴选项B 中的集合不含有任何元素, 故选B.
·3.用适当的符号填空:
·(1)a {a,b,c};(2)0 {x|x =0};(3)Q {x∈R|x +1=0}; (4){0,1} N;(5){0} {x|x=x};(6){2,1} {xTx —3x+2=
0}.
·4.写出集合{a,b,c} 的所有子集.
· [解析]0,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}.
5. 判断下列两个集合之间的关系:
(1)A={x|x<0},B={x|x<1};
(2)A={x|x=3k,k∈N},B={x|x=6z,z∈N};
(3)A={x∈N+|x是4与10的公倍数},B={x|x=20m,m∈N+}.
[解析] (1)A B (2)A B (3)A=B
关键能力·攻重难
题型一集合间关系的判断
例 1(2020·石家庄高一教学质检)指出下列各组集合之间的关系:
(1)A={x|-1
(3)A={x|x —x=0}, ,n∈Z};
(4)A={(x,y)|xy>0},B={(x,y)x>0,y>0 或x<0,y<0};
(5)A={xx=1+a ,a∈N+},B={x|x=a —4a+5,a∈N+}.
题型探究
·[分析] (1)中集合表示不等式,可以根据范围直接判断,也可以利用数 轴判断;(2)根据集合表示数集的意义进行判断;(3)解集合A中方程得到 集合A, 再根据集合B中n分别为奇数、偶数得到集合B, 进行判断;(4) 可以根据集合中元素的特征或者集合的几何意义判断;(5)将集合A中x关 于a的关系式改写成集合B中的形式,再进行判断.
[解析] (1)方法一集合B 中的元素都在集合A 中,但集合A 中有
些元素(比如0,—0.5)不在集合B 中,故B A.
方法二 利用数轴表示集合A,B, 如图所示,由图可知 B A.
(2)∵集合A 是偶数集,集合B 是4的倍数集,∴B A.
(3)A={x|x —x=0}={0,1}.在集合B中,当n 为奇数时,
= 0 , 当n 为偶数时, , ∴B={0,1},∴A=B.
(4)方法一 由 xy>0 得 x>0,y>0 或 x<0,y<0; 由 x>0,y>0 或 x<0,
y<0 得 xy>0, 从 而A=B.
方法二 集 合A 中的元素是平面直角坐标系中第一、三象限内的点
对应的坐标,集合 B 中的元素也是平面直角坐标系中第一、三象限内的 点对应的坐标,从而A=B.
(5)对于任意x ∈A, 有x=1+a =(a+2) -4(a+2)+5.
a∈N+, ∴a+2∈N+,∴x∈B.
由子集的定义知,ASB,
设1∈B, 此时a —4a+5=1, 解得a=2,a∈N+
∵1+a =1 在 a ∈N+时无解,∴14A.
综上所述,A B.
·[归纳提升]判断集合间关系的常用方法
·(1)列举观察法
·当集合中元素较少时,可列出集合中的全部元素,通过定义得出集合之 间的关系.
·(2)集合元素特征法
·首先确定集合的代表元素是什么,弄清集合元素的特征,再利用集合元 素的特征判断关系
·一般地,设A={x|p(x)},B={x|q(x)},①若 由p(x)可推出q(x),则ASB; ②若由q(x)可推出p(x), 则BCA;③ 若p(x),q(x) 可互相推出,则A=B;④ 若由p(x)推不出q(x), 由 q(x)也推不出p(x), 则集合A,B 无包含关系.
·(3)数形结合法
·利用Venn图、数轴等直观地判断集合间的关系.一般地,判断不等式的 解集之间的关系,适合画出数轴
· 【对点练习】①(2020·四川广元外国语高一段考)下列各式中,正确的 个数是( )
·①0={0};D②0S{0};③O∈{0};④0={0};⑤0∈{0};⑥{1}∈{1,2,3};⑦
{1,2}S{1,2,3};⑧{a,b}S{b,a}.
·A.1 B.2
·C.3 D.4
·[解析]0表示空集,没有元素_ {0}有一个元素,则o≠{0},故①错误; ∵空集是任何集合的子集,故②正确;O和{0}都表示集合,故③错误; 0表示元素,{0}表示集合,故④错误;O∈{0},故⑤正确;{1},{1,2,3} 都表示集合,故⑥错误;{1,2}中的元素都是{1,2,3}中的元素,故⑦正确; 由于集合的元素具有无序性,故{a,b}S{b,a}, 故⑧正确.综上,正
确的个数是4个.
题型二确定集合的子集、真子集
设A={x|(x —16)(x +5x+4) =0}, 写出集合A的子集,并指
[分析] 用列举法表示集合A
从子集中除去集合
A本身即得真子集
根据子集中所含元 素的个数写出子集
出其T 哪兰是它的真子集.
·[解析] 由(x -16)(x +5x+4)=0, 得(x-4)(x+1)(x+4) =0, 则方程的 根为x=-4 或x=-1 或x=4.
·故集合A={-4,-1,4}, 由0个元素构成的子集为:0.
·由1个元素构成的子集为:{-4},{-1},{4}.
·由2个元素构成的子集为:{-4,-1},{-4,4},{-1,4}.
·由3个元素构成的子集为:{-4,-1,4}.
·因此集合A的子集为:0,{-4},{-1},{4},{-4,-1},{-4,4},{- 1,4},{-4,-1,4}.
·真子集为:0,{-4},{-1},{4},{-4,-1},{-4,4},{-1,4}.
·[归纳提升](1)若集合A中有n(n∈N+)个元素,则集合A有2n个子集,有 (2n-1) 个真子集,有(2n-1) 个非空子集,有(2n-2) 个非空真子集.
·(2)写出一个集合的所有子集时,首先要注意两个特殊的子集:0和自
身.其次,依次按含有1个元素的子集,含有2个元素的子集,含有3个 元素的子集……——写出,保证不重不漏.
A.2 B.6
C.7 D.8
·[解析]由题意知,集合A可以为{a,b},{a,b,c},{a,b,d},{a,b, e},{a,b,c,d},{a,b,c,e},{a,b,d ,e}.
【对点练习】②满足{a,b}EA {a,b,c,d,e}的集合A 的个数
是(C)
题型三 由集合间的关系求参数范围问题
例 3 已知集合A={x|-3≤x≤4},B={x|2m—1
·[分析]借助数轴分析,注意B是否为空集.
·[解析] (1)因为BCA,
· 当B=0 时 ,m+1≤2m-1, 解 得m≥2.
(2)当B≠0 时,有
解得— 1≤m<2, 综上得m≥—1.
·[归纳提升](1)分析集合间的关系时,首先要分析、简化每个集合.(2) 借助数轴,利用数轴分析法,将各个集合在数轴上表示出来,以形定数, 还要注意验证端点值,做到准确无误, 一般含“=”用实心点表示,不 含“=”用空心点表示.
·此类问题要注意对空集的讨论.
·【对点练习】③(1)已知集合A={— 1,3,2m—1},集合 若
BGA, 则 实 数m= ;
·(2)已知集合A={x|x<-1, 或x>4},B={x|2a≤x≤a+3}, 若BSA, 求实数a 的取值范围.
·[解析](1)因为BSA, 所以m =2m-1,
·即(m-1) =0, 所以m=1.当m=1 时 ,A={-1,3,1},B={3,1}, 满足BCA, 故m=1.
(2)当B=0 时,只需2a>a+3, 即 a>3;
当B≠o 时,根据题意作出如图所示的数轴,
-1 4 2a a+3 X
2a a+3 -1 4 X
综上可得,实数a 的取值范围为a<—4 或 a>2.
, 解 得a<—4 或 2
已知集合A={—1,1},B={x|ax+1
所 例 4(值的集合为( )
·A.{—1} B.{1} D
·C.{—1,1}D.{—1,0,1}
因此有 所 以a=±1,
[错解] 因为 而
=0}, 若 BSA, 则 实 数 的
· 忽视“空集”的存在
误区警示
故 选C.
[错因分析] 空集是一个特殊而重要的集合,它不含任何元素,记为
0.在解隐含有空集参与的集合问题时,极易忽视空集的特殊性而导致错 解.本例求解过程中有两处错误, 一是方程ax=—1 的解不能写成x= 一
,二是忽视了BSA 时 ,B 可以为空集 .事实上a=0 时,方程无解.
[正解] 因为BSA, 所以当B≠a,即a≠0时 , 因
此有 所以a=±1; 当 B=0, 即 a=0 时满足条件.
综上可得实数a 的所有可能取值的集合是{—1,0,1}.故选D.
·[方法点拨]已知两个集合之间的关系求参数时,要根据集合间的关系 来确定元素之间的关系,需关注子集是否为空集.
·一般地,当集合为有限集时,往往通过列方程或方程组来处理,此时需 注意集合中元素的互异性;当集合为连续型无限集时,往往借助数轴列 不等式或不等式组来求解,要注意运用分类讨论、数形结合等思想方法, 尤其需注意端点值能否取到.
·分类讨论思想的应用
·分类讨论,通俗地讲,就是“化整为零,各个击破”.分类讨论要弄清 楚是依据哪个参数进行分类的,采用的标准是什么.分类讨论的原则是: (1)不重不漏;(2)一次分类只能按所确定的同一个标准进行.
学科素养
+1)=0,
当 a=0 时,集合B 中的三个元素相同,不满足集合中元素的互异性,
故a≠0,c —2c+1=0, 即 c=1.
当c=1 时,集合B 中的三个元素也相同,∴c=1 舍去,即此时无解.
·[分析] 根据集合相等的定义和集合元素的互异性求解.由于A=B, 元 素a 在两个集合中都有,故其余两个元素的情况需分类讨论.
消去b 得a+ac —2ac=0, 即 a(c —2c
已知集合A={a,a+b,a+2b},B={a,ac,ac },
[解析] ①
若A=B,
例 5
且
求 C
②若 消去b 得 2ac —ac—a=0,
即a(2c —c—1)=0,∵a≠0,∴2c —c—1=0,
∴A=B. 综上可知
即(c-1)(2c+1)=0. 又∵c≠1,∴
当 时
,
·[归纳提升] 1.两个集合相等,则所含元素完全相同,与顺序无关,但 要注意检验,排除与集合元素互异性或与已知相矛盾的情形.
·2.若两个集合中元素均为无限多个,要看两集合的代表元素是否一致, 且看代表元素满足条件是否一致,若均一致,则两集合相等.
课堂检测·固双基
点击进入WORD
文档
素养作业·提技能
点击进入WORD
文档
演示完毕
谢谢欣赏
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
