集合间的基本关系 课件(共39张PPT) 高一上学期数学人教A版(2019)必修第一册
文档属性
| 名称 | 集合间的基本关系 课件(共39张PPT) 高一上学期数学人教A版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 15:38:30 | ||
图片预览











文档简介
(共39张PPT)
1.1.2集合间本关系
教材分析:课程标准——集合
· 1 . 集合
· 在高中数学课程中,集合是刻画一类事物的语言和工具。本单元的学习, 可以帮助学生使用集合的语言简洁、准确地表述数学的研究对象,学会用 数学的语言表达和交流,积累数学抽象的经验。
· 内容包括:集合的概念与表示、集合的基本关系、集合的基本运算。
● (1)集合的概念与表示
·①通过实例,了解集合的含义,理解元素与集合的“属于”关系。
·②针对具体问题,能够在自然语言和图形语言的基础上,用符号语言刻画
集合。
· ③在具体情境中,了解全集与空集的含义。
● (2)集合的基本关系
· 理解集合之间包含与相等的含义,能识别给定集合的子集。
(3)集合的基本运算
·①理解两个集合的并集与交集的含义,能求两个集合的并集与交集。
·②理解在给定集合中一个子集的补集的含义,能求给定子集的补集。
· ③能使用Venn图表达集合的基本关系与基本运算,体会图形对理解抽象 概念的作用。
1.内容
集合之间的包含与相等的含义;子集、真子集与空集的概念;集合的 Venn图表示。
2.内容分析
本节类比实数,发现和提出“集合是否像实数一样具有相等关系、大 小关系”的问题,抽象概括出包含关系,并从子集角度再认识相等关 系。
包含关系是集合的基本关系,包含关系和相等关系也都是从元素与集 合之间的关系定义集合之间的关系。也就是说,当我们判断集合间关 系时,其实是回归到了元素与集合的关系。明确了这一点,对于辨析 属于关系、包含关系及理解其符号表示都是很有帮助的。如“”就是 “对于任意”。
符号化是数学的重要特征。在集合的学习中,需要建立符号表示和数 学意义之间的联系,Venn图则是梳理集合间的关系以及后面所学的运 算的直观且有效的工具。通过各种问题,建立自然语言、符号语言和 图形语言 (Venn图)之间的联系,有利于表示数学问题,也有助于提 升学生数学抽象素养。
结合以上分析,确定本节课的教学重点:集合间包含与相等的含义。
二、学习目标
(1)理解集合之间的包含与相等的含义;
(2)能识别给定集合的子集,了解空集含义;
(3)能进行自然语言、图形语言(Venn 图)、符号语言间的转换,提 升数学抽象素养。
三、学情分析
学生在义务教育阶段数学学习中,已经接触过集合,对于数集、点集 等有了一定的感性认识。从初中到高中,从直观到抽象,了解集合的含义 及其性质,并不困难。难点在于两种关系的识别 元素与集合、集合与 集合,特别是符号语言的表述,提升了这部分内容学习的抽象度,
此外,对于空集这个特殊的集合,由于其本质特征“不含任何元素” 无法用列举法或描述法直观地表达出来,所以用一个单独的符号“”来标 记。看不见、摸不着,这也是让学生感到困难的原因。另外,空集也容易 和一些集合混淆,比如集合“{0}”,“{0}”是含有一个元素的集合,集 合中的元素是“0”,而是不含任何元素的,因此与{0}之间的关系是
{0}。
本节课的教学难点是集合基本关系的符号表述及识别,对空集的了解。
【引一引★温故知新】
集合与集合
之向呢
实数有大小关系
如 :5< 7,5>3
实数有相等关系
如:5=5
观察以下几组集合,并指出它们元素间的关系:
①A={1,2,3},B={1,2,3,4,5};
②设 A为某校高一(2)班全体女生组成的集合,B为这个 班全体学生组成的集合
③A={xIx 是两边相等的三角形},
B={xl x是等腰三角形}.
【想一想★得出新知】
一般地,对于两个集合A 、B, 如果集合A中任
意一个元素都是集合B中的元素,我们就说这两个集 合有包含关系,称集合A 为集合B的子集.记作:
ACB (或B2A)
读 作:“A 含于B”(或“B包含A”)
【说一说★本节新知】
1 . 子集
【说一说★本节新知】
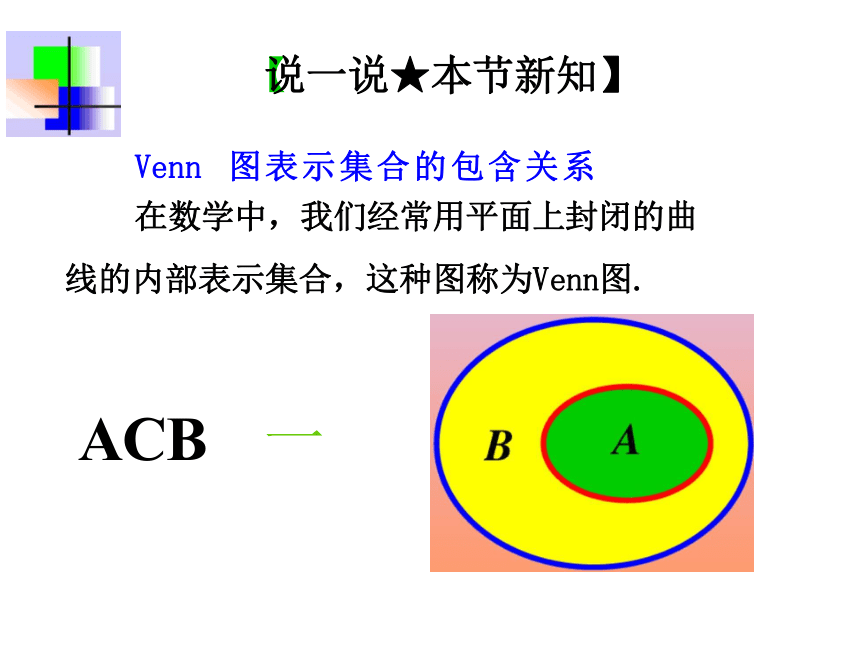
线的内部表示集合,这种图称为Venn图.
在数学中,我们经常用平面上封闭的曲
Venn 图表示集合的包含关系
ACB 一
观察以下几组集合,并指出它们元素间的关系:
① A={1,3,5,7,9},B={9,7,5,3,1}
②A={a,b,c,d},B={b,c,d,a};
③ A={xIx 是两边相等的三角形},
B={xl x是等腰三角形}.
【想一想★得出新知】
C 2.集合相等 如果集合A 是集合B的子集(即ASB), 且集合B 是集合A 的子集(即BSA) 此时集合A 与集合B中的 元素是一样的,我们称集合A 与集合B相等. 记 作 :A=B.
【说一说★本节新知】
观察以下几组集合,并指出它们元素间的关系:
①A={1,2,3},B={1,2,3,4,5};
②A={-1,0,1},B={-1,0,1,2}
③A={a,c,d},B={a,b,c,d}
【想一想★得出新知】
如果集合AEB, 但存在元素x ∈B, 且x ∈A,
我们称集合A是集合B的真子集.
记作:A B ( 或B A ).
读 作 :“A 真含于B”( 或“B 真包含A”)
【说一说★本节新知】
3.真子集
【说一说★本节新知】
4 . 子集的有关性质
(1).任何一个集合是它本身的子集,即AEA .
(2).对于集合A 、B 、C, 如 果ASB
(3).对于集合A 、B 、C, 如 果AEB
(4).对于集合A 、B 、C, 如 果AEB (5).对于集合A 、B 、C, 如 果ASB
那么AGC.
那么AEC.
那么AEC. 那么AEC.
且BSC
且BEC
且BCC 且BEC
(6).对于集合A 、B 、C, 如 果A=B 且B=C 那么A=C.
不含任何元素的集合叫做空集,记为0.
规定:空集是任何集合的子集,即 S A .
空集是任何非空集合的真子集.
即 : 年B. (B≠0)
【说一说★本节新知】
5.空集
1.包含关系{a}CA与属于关系a ∈A有什么区别
2.集合A 年B 与集合ACB 有什么区别 3.0,{0},0与{0}四者之间有什么关系
【议一议★深化概念】
【听一听★更上一层】
例1.写出集合{a,b}的所有子集,并指出哪
些是它的真子集.
解:集合{a,b}的所有子集为
,{a},{b},{a,b}
真子集为:O,{a},{b}
写出集合{a,b,c} 的所有子集,并指出它的真子集. 解:没有元素的子集:0;
有1个元素的子集:{a},{b},{c} ;
有2个元素的子集:{a,b},{a,c},{b,c};
有3个元素的子集:{a,b,c}.
集合{a,b,c}的所有子集为:
,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}.
集合{a,b,c}的所有真子集为:
,{a},{b},{c},{a,b},{a,c},{b,c}.
【听一听★更上一层
变式
· 含n个元素的集合的所有子集的个数是2n,
·所有真子集的个数是2n-1,非空真子集数
为2n-2.
题型1 集合的子集、真子集问题
例1 (1)满足{a,b}c Mc {a,b,C,d,e}的集合M的
个数为( )
A.6 B.7
C.8 D.9
(2)已知集合A={(x,y )|x+y=2,X, y∈ N}, 试写出A 的
所有子集.
答案:
(1)A
(2)0,{(0,2)},{(1,1)},{(2,0)},{(0,2),(1,1)}, {(0,2),(2,0)},{(1,1),(2,0)},{(0,2),(1,1),(2,
0)}
解析答案
方法归纳
1. 假设集合A 中含有n 个元素,则有:
(1)A 的子集有2n个;
(2)A 的非空子集有(2n—1)个;
(3)A的真子集有(2n—1)个;
(4)A的非空真子集有(2n—2)个.
2. 求给定集合的子集的两个注意点:
(1)按子集中元素个数的多少,以一定的顺序来写; (2)在写子集时要注意不要忘记空集和集合本身.
跟踪训练1(1)若集合A={x∈Z|-1集个数为( )
A.1 B.2
C.3 D.4
(2)写出满足{3,4} c P={0,1,2,3,4}的所有集合P.
答案:
(1)C
(2){0,3,4},{1,3,4},{2,3,4},{0,1,3,4},{0, 2,3,4},{1,2,3,4},{0,1,2,3,4}
解析答案
题型2 集合间关系的判断
例2 指出下列各组集合之间的关系:
(1)A={x|-1(2)A={x|x=2n,n∈Z},B={xx=4n,n∈Z};
(3)A={(x,y)|xy>0},B={(x,y)|x>0,y>0或x<0,y <0}.
(4)A={x|x=1+a2,a∈N*},B={x|x=a - 4a+5, a ∈N*}.
解析
方法归纳
判断集合间关系的方法
(1)用定义判断
首先,判断一个集合A 中的任意元素是否属于另一集合B, 若是,则ACB, 否 则A 不是B 的子集;
其次,判断另一个集合B 中的任意元素是否属于第一个集合 A, 若是,则BSA, 否 则B 不是A的子集;
若既有ACB, 又 有Bs A, 则A=B.
(2)数形结合判断
对于不等式表示的数集,可在数轴上标出集合的元素,直 观地进行判断,但要注意端点值的取舍.
跟踪训练2 (1)若集合M={x|x-1=0},T={-1,0,
1}, 则M 与 T的关系是( )
A.Mc T B.Mc T
C.M=T D.MtT
(2)设M={ 菱形}, N={ 平行四边形},P={ 四边形},Q=
{正方形},则这些集合之间的关系为( )
A.PcNcMcQ B.QEMcNcP
C.PEMENcQ D.QCNcMEP
答案: (1)A (2)B
解析答案
题型3 根据集合间关系求参数(取值范围)
例3 已知集合A={x1求
解析
方法归纳
(1)分析集合关系时,首先要分析、简化每个集合.
(2)此类问题通常借助数轴,利用数轴分析法,将各个集合 在数轴上表示出来,以形定数,还要注意验证端点值,做到 准确无误, 一般含“=”用实心点表示,不含“=”用空心 点表示.
(3)此类问题还应注意“空集”这一 “陷阱”,尤其是集合 中含有字母参数时,初学者会想当然认为非空集合而丢解, 因此分类讨论思想是必需的.
跟踪训练3 已知集合A={x1解析:∵ACB,∴B≠o, 则有:
,解之得:m≤-2. ∴实数m 的取值范围是{mm≤-2}.
解析
易错辨析 忽略空集的特殊性致误
例4 设M={x|x -2x-3=0},N={x|ax-1=0}, NSM, 求所有满足条件的a的取值集合.
解析: 由NEM,M={x|x -2x-3=0}={-1,3}, 得N= 或N={-1} 或N={3}.
当N= 时 ,ax-1=0 无解,即a=0. 当N={-1} 时,由 , 得a=-1. 当N={3} 时 , 由 , 得 ●
故满足条件的a的取值集合为 ,0,
若
解析
。
易错原因
纠错心得
忽 略 了N=0 这 种情况.
空集是任何集合的子集,解 这类问题时, 一定要注意“ 空集优先”的原则.
易错警示
1. 集 合A={—1,0,1 }, 在A的子集中,含有元素0的子集
共有( )
A.2 个 B.4 个
C.6 个 D.8 个
课 堂 十 分 钟
答案: B
答案
2.(多选)下列说法正确的是( )
C. 若a ∈N,则 一atN D.π4Q
答案: BD
A. B.oS{0}
答案
数 a的 值 为 ( ) A.1 或2 B.0 或 1
C. 0或2 D. 0或1或2
3. 已知集合A={xax=X2},B={0,1,2}, 若ACB, 则
答案: D
答案
4. 设集合A={x∈R|x2+x-1=0},B={x∈R|x —x+1= 0},则集合A,B 之间的关系是
答案
5.已知集合A={x|1≤x≤2},B={x1≤x≤a,a≥1}.
(2)若BcA, 求a的取值范围.
解析:(1)若A B, 由图可知,a>2.
(1)若AC B,求a的取值范围.
(2)若BCA, 由图可知,1≤a≤2.
解析
1. 集 合A={—1,0,1 }, 在A的子集中,含有元素0的子集
共有( )
A.2 个 B.4 个
C.6 个 D.8 个
课 堂 十 分 钟
答案: B
答案
2.(多选)下列说法正确的是( )
C. 若a ∈N,则 一atN D.π4Q
答案: BD
A. B.oS{0}
答案
数 a的 值 为 ( ) A.1 或2 B.0 或 1
C. 0或2 D. 0或1或2
3. 已知集合A={xax=X2},B={0,1,2}, 若ACB, 则
答案: D
答案
4.设集合A={x∈R|x +x-1=0},B={x∈R|x —x+1=则集合A,B 之官的关系是 —_——— ·
答案
5. 已知集合A={x|1≤x≤2},B={x1≤x≤a,a≥1}. (1)若A B, 求a 的取值范围 .
(2)若BcA, 求a的取值范围.
解析:(1)若A B, 由图可知,a>2.
(2)若BCA, 由图可知,1≤a≤2.
解析
1.1.2集合间本关系
教材分析:课程标准——集合
· 1 . 集合
· 在高中数学课程中,集合是刻画一类事物的语言和工具。本单元的学习, 可以帮助学生使用集合的语言简洁、准确地表述数学的研究对象,学会用 数学的语言表达和交流,积累数学抽象的经验。
· 内容包括:集合的概念与表示、集合的基本关系、集合的基本运算。
● (1)集合的概念与表示
·①通过实例,了解集合的含义,理解元素与集合的“属于”关系。
·②针对具体问题,能够在自然语言和图形语言的基础上,用符号语言刻画
集合。
· ③在具体情境中,了解全集与空集的含义。
● (2)集合的基本关系
· 理解集合之间包含与相等的含义,能识别给定集合的子集。
(3)集合的基本运算
·①理解两个集合的并集与交集的含义,能求两个集合的并集与交集。
·②理解在给定集合中一个子集的补集的含义,能求给定子集的补集。
· ③能使用Venn图表达集合的基本关系与基本运算,体会图形对理解抽象 概念的作用。
1.内容
集合之间的包含与相等的含义;子集、真子集与空集的概念;集合的 Venn图表示。
2.内容分析
本节类比实数,发现和提出“集合是否像实数一样具有相等关系、大 小关系”的问题,抽象概括出包含关系,并从子集角度再认识相等关 系。
包含关系是集合的基本关系,包含关系和相等关系也都是从元素与集 合之间的关系定义集合之间的关系。也就是说,当我们判断集合间关 系时,其实是回归到了元素与集合的关系。明确了这一点,对于辨析 属于关系、包含关系及理解其符号表示都是很有帮助的。如“”就是 “对于任意”。
符号化是数学的重要特征。在集合的学习中,需要建立符号表示和数 学意义之间的联系,Venn图则是梳理集合间的关系以及后面所学的运 算的直观且有效的工具。通过各种问题,建立自然语言、符号语言和 图形语言 (Venn图)之间的联系,有利于表示数学问题,也有助于提 升学生数学抽象素养。
结合以上分析,确定本节课的教学重点:集合间包含与相等的含义。
二、学习目标
(1)理解集合之间的包含与相等的含义;
(2)能识别给定集合的子集,了解空集含义;
(3)能进行自然语言、图形语言(Venn 图)、符号语言间的转换,提 升数学抽象素养。
三、学情分析
学生在义务教育阶段数学学习中,已经接触过集合,对于数集、点集 等有了一定的感性认识。从初中到高中,从直观到抽象,了解集合的含义 及其性质,并不困难。难点在于两种关系的识别 元素与集合、集合与 集合,特别是符号语言的表述,提升了这部分内容学习的抽象度,
此外,对于空集这个特殊的集合,由于其本质特征“不含任何元素” 无法用列举法或描述法直观地表达出来,所以用一个单独的符号“”来标 记。看不见、摸不着,这也是让学生感到困难的原因。另外,空集也容易 和一些集合混淆,比如集合“{0}”,“{0}”是含有一个元素的集合,集 合中的元素是“0”,而是不含任何元素的,因此与{0}之间的关系是
{0}。
本节课的教学难点是集合基本关系的符号表述及识别,对空集的了解。
【引一引★温故知新】
集合与集合
之向呢
实数有大小关系
如 :5< 7,5>3
实数有相等关系
如:5=5
观察以下几组集合,并指出它们元素间的关系:
①A={1,2,3},B={1,2,3,4,5};
②设 A为某校高一(2)班全体女生组成的集合,B为这个 班全体学生组成的集合
③A={xIx 是两边相等的三角形},
B={xl x是等腰三角形}.
【想一想★得出新知】
一般地,对于两个集合A 、B, 如果集合A中任
意一个元素都是集合B中的元素,我们就说这两个集 合有包含关系,称集合A 为集合B的子集.记作:
ACB (或B2A)
读 作:“A 含于B”(或“B包含A”)
【说一说★本节新知】
1 . 子集
【说一说★本节新知】
线的内部表示集合,这种图称为Venn图.
在数学中,我们经常用平面上封闭的曲
Venn 图表示集合的包含关系
ACB 一
观察以下几组集合,并指出它们元素间的关系:
① A={1,3,5,7,9},B={9,7,5,3,1}
②A={a,b,c,d},B={b,c,d,a};
③ A={xIx 是两边相等的三角形},
B={xl x是等腰三角形}.
【想一想★得出新知】
C 2.集合相等 如果集合A 是集合B的子集(即ASB), 且集合B 是集合A 的子集(即BSA) 此时集合A 与集合B中的 元素是一样的,我们称集合A 与集合B相等. 记 作 :A=B.
【说一说★本节新知】
观察以下几组集合,并指出它们元素间的关系:
①A={1,2,3},B={1,2,3,4,5};
②A={-1,0,1},B={-1,0,1,2}
③A={a,c,d},B={a,b,c,d}
【想一想★得出新知】
如果集合AEB, 但存在元素x ∈B, 且x ∈A,
我们称集合A是集合B的真子集.
记作:A B ( 或B A ).
读 作 :“A 真含于B”( 或“B 真包含A”)
【说一说★本节新知】
3.真子集
【说一说★本节新知】
4 . 子集的有关性质
(1).任何一个集合是它本身的子集,即AEA .
(2).对于集合A 、B 、C, 如 果ASB
(3).对于集合A 、B 、C, 如 果AEB
(4).对于集合A 、B 、C, 如 果AEB (5).对于集合A 、B 、C, 如 果ASB
那么AGC.
那么AEC.
那么AEC. 那么AEC.
且BSC
且BEC
且BCC 且BEC
(6).对于集合A 、B 、C, 如 果A=B 且B=C 那么A=C.
不含任何元素的集合叫做空集,记为0.
规定:空集是任何集合的子集,即 S A .
空集是任何非空集合的真子集.
即 : 年B. (B≠0)
【说一说★本节新知】
5.空集
1.包含关系{a}CA与属于关系a ∈A有什么区别
2.集合A 年B 与集合ACB 有什么区别 3.0,{0},0与{0}四者之间有什么关系
【议一议★深化概念】
【听一听★更上一层】
例1.写出集合{a,b}的所有子集,并指出哪
些是它的真子集.
解:集合{a,b}的所有子集为
,{a},{b},{a,b}
真子集为:O,{a},{b}
写出集合{a,b,c} 的所有子集,并指出它的真子集. 解:没有元素的子集:0;
有1个元素的子集:{a},{b},{c} ;
有2个元素的子集:{a,b},{a,c},{b,c};
有3个元素的子集:{a,b,c}.
集合{a,b,c}的所有子集为:
,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}.
集合{a,b,c}的所有真子集为:
,{a},{b},{c},{a,b},{a,c},{b,c}.
【听一听★更上一层
变式
· 含n个元素的集合的所有子集的个数是2n,
·所有真子集的个数是2n-1,非空真子集数
为2n-2.
题型1 集合的子集、真子集问题
例1 (1)满足{a,b}c Mc {a,b,C,d,e}的集合M的
个数为( )
A.6 B.7
C.8 D.9
(2)已知集合A={(x,y )|x+y=2,X, y∈ N}, 试写出A 的
所有子集.
答案:
(1)A
(2)0,{(0,2)},{(1,1)},{(2,0)},{(0,2),(1,1)}, {(0,2),(2,0)},{(1,1),(2,0)},{(0,2),(1,1),(2,
0)}
解析答案
方法归纳
1. 假设集合A 中含有n 个元素,则有:
(1)A 的子集有2n个;
(2)A 的非空子集有(2n—1)个;
(3)A的真子集有(2n—1)个;
(4)A的非空真子集有(2n—2)个.
2. 求给定集合的子集的两个注意点:
(1)按子集中元素个数的多少,以一定的顺序来写; (2)在写子集时要注意不要忘记空集和集合本身.
跟踪训练1(1)若集合A={x∈Z|-1
A.1 B.2
C.3 D.4
(2)写出满足{3,4} c P={0,1,2,3,4}的所有集合P.
答案:
(1)C
(2){0,3,4},{1,3,4},{2,3,4},{0,1,3,4},{0, 2,3,4},{1,2,3,4},{0,1,2,3,4}
解析答案
题型2 集合间关系的判断
例2 指出下列各组集合之间的关系:
(1)A={x|-1
(3)A={(x,y)|xy>0},B={(x,y)|x>0,y>0或x<0,y <0}.
(4)A={x|x=1+a2,a∈N*},B={x|x=a - 4a+5, a ∈N*}.
解析
方法归纳
判断集合间关系的方法
(1)用定义判断
首先,判断一个集合A 中的任意元素是否属于另一集合B, 若是,则ACB, 否 则A 不是B 的子集;
其次,判断另一个集合B 中的任意元素是否属于第一个集合 A, 若是,则BSA, 否 则B 不是A的子集;
若既有ACB, 又 有Bs A, 则A=B.
(2)数形结合判断
对于不等式表示的数集,可在数轴上标出集合的元素,直 观地进行判断,但要注意端点值的取舍.
跟踪训练2 (1)若集合M={x|x-1=0},T={-1,0,
1}, 则M 与 T的关系是( )
A.Mc T B.Mc T
C.M=T D.MtT
(2)设M={ 菱形}, N={ 平行四边形},P={ 四边形},Q=
{正方形},则这些集合之间的关系为( )
A.PcNcMcQ B.QEMcNcP
C.PEMENcQ D.QCNcMEP
答案: (1)A (2)B
解析答案
题型3 根据集合间关系求参数(取值范围)
例3 已知集合A={x1
解析
方法归纳
(1)分析集合关系时,首先要分析、简化每个集合.
(2)此类问题通常借助数轴,利用数轴分析法,将各个集合 在数轴上表示出来,以形定数,还要注意验证端点值,做到 准确无误, 一般含“=”用实心点表示,不含“=”用空心 点表示.
(3)此类问题还应注意“空集”这一 “陷阱”,尤其是集合 中含有字母参数时,初学者会想当然认为非空集合而丢解, 因此分类讨论思想是必需的.
跟踪训练3 已知集合A={x1
,解之得:m≤-2. ∴实数m 的取值范围是{mm≤-2}.
解析
易错辨析 忽略空集的特殊性致误
例4 设M={x|x -2x-3=0},N={x|ax-1=0}, NSM, 求所有满足条件的a的取值集合.
解析: 由NEM,M={x|x -2x-3=0}={-1,3}, 得N= 或N={-1} 或N={3}.
当N= 时 ,ax-1=0 无解,即a=0. 当N={-1} 时,由 , 得a=-1. 当N={3} 时 , 由 , 得 ●
故满足条件的a的取值集合为 ,0,
若
解析
。
易错原因
纠错心得
忽 略 了N=0 这 种情况.
空集是任何集合的子集,解 这类问题时, 一定要注意“ 空集优先”的原则.
易错警示
1. 集 合A={—1,0,1 }, 在A的子集中,含有元素0的子集
共有( )
A.2 个 B.4 个
C.6 个 D.8 个
课 堂 十 分 钟
答案: B
答案
2.(多选)下列说法正确的是( )
C. 若a ∈N,则 一atN D.π4Q
答案: BD
A. B.oS{0}
答案
数 a的 值 为 ( ) A.1 或2 B.0 或 1
C. 0或2 D. 0或1或2
3. 已知集合A={xax=X2},B={0,1,2}, 若ACB, 则
答案: D
答案
4. 设集合A={x∈R|x2+x-1=0},B={x∈R|x —x+1= 0},则集合A,B 之间的关系是
答案
5.已知集合A={x|1≤x≤2},B={x1≤x≤a,a≥1}.
(2)若BcA, 求a的取值范围.
解析:(1)若A B, 由图可知,a>2.
(1)若AC B,求a的取值范围.
(2)若BCA, 由图可知,1≤a≤2.
解析
1. 集 合A={—1,0,1 }, 在A的子集中,含有元素0的子集
共有( )
A.2 个 B.4 个
C.6 个 D.8 个
课 堂 十 分 钟
答案: B
答案
2.(多选)下列说法正确的是( )
C. 若a ∈N,则 一atN D.π4Q
答案: BD
A. B.oS{0}
答案
数 a的 值 为 ( ) A.1 或2 B.0 或 1
C. 0或2 D. 0或1或2
3. 已知集合A={xax=X2},B={0,1,2}, 若ACB, 则
答案: D
答案
4.设集合A={x∈R|x +x-1=0},B={x∈R|x —x+1=则集合A,B 之官的关系是 —_——— ·
答案
5. 已知集合A={x|1≤x≤2},B={x1≤x≤a,a≥1}. (1)若A B, 求a 的取值范围 .
(2)若BcA, 求a的取值范围.
解析:(1)若A B, 由图可知,a>2.
(2)若BCA, 由图可知,1≤a≤2.
解析
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
