命题的的否定【新教材】人教A版高中数学必修第一册优秀课件(共22张PPT)
文档属性
| 名称 | 命题的的否定【新教材】人教A版高中数学必修第一册优秀课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第一章集合与常用 逻辑用语
1.5.2
全称量词命题和存在量 词命题的否定
科学家的自我否定
● 不久前,著名科学杂志自然发表了英国物理学家霍金
的一篇论文。他在文中提出,自己当初对世界的认识是有 缺陷的。按照经典理论,黑洞内部不会放过任何物质信息, 但最新理论却证明能量和信息能够逃离黑洞,这样,黑洞 是否真的存在就值得怀疑了
作为认识宇宙的重要突破,提出论证黑洞曾为,霍金
赢得世界声誉。质疑黑洞的存在,无疑对是对自己的否定。 这不是霍金第一次自我否定,两年前当一种与上帝粒子特 性一致的新粒子,希格斯粒子被发现时,霍金向她之前的, 打赌对象,预言上帝粒子存在的物理学家彼得希格斯寄去 一张100美元的支票,承认自己当年的无知。
· 霍金的自我否定并没有损害他在科学界的形象,反而赢 得了更多的掌声,同时也使他对宇宙的认识,更前进了一 步。
写出下列命题的否定:
(1)所有的矩形都是平行四边形;
(2)每一个素数都是奇数; (3) x ∈R,x +| x|≥0.
它们与原命题在形式上有什么变化
一个命题和它的否定
不能同时为真命题,也不 能同时为假命题,只能
一真一假.
探究一
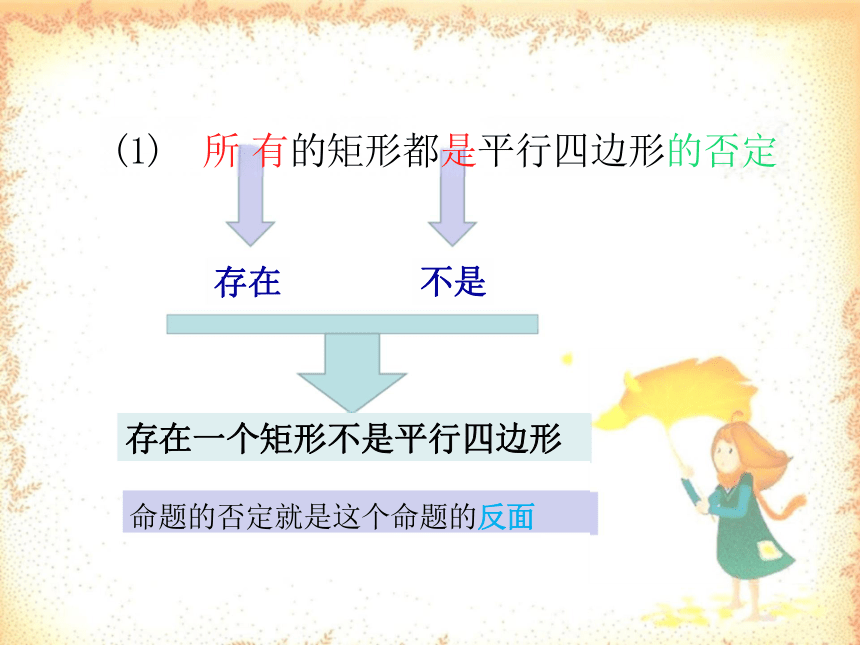
命题的否定就是这个命题的反面
存在一个矩形不是平行四边形
(1) 所 有的矩形都是平行四边形的否定
存在
不是
(2)的否定是“并非每一个素数都是奇数”,
也就是说,
存在一个素数不是奇数;
(3)的否定是“并非所有的x∈R,x+|x|≥0 ”
也就是说,
3x∈R,x+|xl <0
·全称量词命题: Vx∈R,p (x),
·它的否定:3 x∈R,-p(x) .
·也就是说,全称量词命题的否定是存在量 词命题.
概念1
1.全称量词命题的否定一定是存在
量词命题吗
提 示 :是,因为全称量词的否定一定是存在 量词,所以全称量词命题的否定一定是存在量词 命题 .
2.用自然语言描述的全称量词
命题 的否定形式唯一吗
提 示 :不唯一,如“所有的菱形都是平行四 边形”,它的否定是“并不是所有的菱形都是平 行四边形”,也可以是“有些菱形不是平行四边 形” .
思考
例题讲解
例1写出下列全称量词命题的否定:
(1)所有能被3整除的整数都是奇数;
(2)每一个四边形的四个顶点在同一个圆上;
( 3 ) 对 任 意x ∈Z,x 的个位数字不等于3.
解 : (1)该命题的否定: 存在 一个能被3整除 的整数不是奇数.
(2)该命题的否定: 存 在一个四边形,它 的四个顶点不在同一个圆上.
(3)该命题的否定:3 x∈Z,x 的个位数字 等于3.
练习写出下列全称量词命题的否定,并判断真假: (1)Vx∈R,1-
(2)所有的正方形都是矩形.
(3)对任意x ∈Z,x 的个位数字不等于3.
(4)正数的绝对值是它本身.
解(1)该命题的 :3x∈R,1- (x>
R, ,所以- <0)
恒成立,所以这是一个假命题.
(2)该命题的否定:至少存在一个正方形不是矩形,
假命题.
(3)该命题的否定:至少存在一个x∈Z,x 的个位数
等于3,因为0 =0,1 =1,2 =4,3 =9,4 =16,
52=25,6 =36,72=49,82=64,92=81, …
所以这是一个假命题.
·
写出下列命题的否定:
(1)存在一个实数的绝对值是正数;
(2)有些平行四边形是菱形;
(3) 3x∈R,x —2x+3=0.
它们与原命题在形式上有什么变化
探究二
(1) 存在一个实数的绝对值是正数的否定
所有实数的绝对值都不是正数
命题的否定就是这个命题的反面
所有
不是
概念2
对含有一个量词的存在量词命题的否定, 有下面的结论:
存在量词命题:
3x∈R, -p(x)
它的否定:
Vx∈R,p(x)
也就是说,存在量词命题的否定是全称量 词命题.
原词 否定词 原词
否定词
等于 不等于 至多一个
至少两个
大于 不大于 至少一个
一个也没有
小于 不小于 任意
某个
是 不是 所有的
某些
都是 不都是
否定词总结
小结
1. 对全称命题否定的步骤
第一步改变量词:把全称量词换为恰当 的存在量词;
第二步否定性质:原命题中的“p(x)成立” 改为“非p(x)成立”。
2. 对存在性命题否定的步骤
第一步改变量词:把存在量词换为恰当 的全称量词;
第二步否定性质:原命题中的“p(x)成立” 改为“非p(x) 成立”。
练习
命题“3x∈R,x +2x+3=0”的否定是
【解析】因为存在量词命题的 否定是全称量词命题,所以命
题“3x ∈R,x +2x+3=0”
否定是“Vx∈R,
x2+2x+3≠0”
答案:Vx∈R,x +2x+3≠0
的
为什么存在量词命题的否定
一定是全称量词命题
提示:因为对“有的”,“存在 一个”,“至少一个”等词语的否定 是“都没有”,“都不存在”, “全 都不”等,所以存在量词命题的否定 一定是全称量词命题.
思考
“一般命题的否定”与“全称量词
命题和存在量词命题的否定”有
什么区别与联系
(1)一般命题的否定通常是保留条件否定其结论, 得到真假性完全相反的两个命题;全称量词命题和存 在量词命题的否定要在否定结论p(x)的同时,改变量 词的属性,即全称量词改为存在量词,存在量词改为 全称量词.
(2)与一般命题的否定相同,全称量词命题和 存在量词命题的否定的关键也是对关键词的否定.因 此,对全称量词命题和存在量词命题的否定,应根据 命题所叙述的对象的特征,挖掘其中的量词.全称量 词命题的否定与全称量词命题的真假性相反;存在量 词命题的否定与存在量词命题的真假性相反.
思考
练习
1. 写出下列命题的否定,并判断其真假.
(1)p: 所有的方程都有实数解;
(2)q:Vx∈R,4x —4x+1≥0;
(3)r:3x ∈R,x +2x +2≤0;
(4)s:某些平行四边形是菱形.
解 (1)非p: 存在一个方程没有实数解,真命 题.比如方程x +1=0 就没有实数解.
(2)非q:3x ∈R, 使 4x0(2)一4x +1<0, 假命 题 .这里由于Vx∈R,4x —4x+1=(2x—1) ≥0 恒成 立,是真命题,所以非q是假命题.
(3)非r:Vx∈R,x +2x+2>0, 真命题.
(4)非s: 每一个平行四边形都不是菱形,假命题。
2.把下列命题进行否定,并写在横线上.
(1)p:有些三角形是直角三角
(2)q: 所有的质数都是奇
(3)r所 有的所酌三角形都不是直角三角形
(4):有些实数的数愿数不是奇数
(3)有的人不睡觉
(4)所有实数的相反数都不比本身大
形 .
数.
觉 .
大.
练习
练习
3. 在本节,我们介绍了命题的否定的概念,知道一个命题 的否定仍是一个命题,它和原先的命题只能一真一假,不 能同真或同假.
在数学中,有很多“若p, 则q”形式的命题,有的是 真命题,有的是假命题.例如:
① 若x>1, 则 2x+1>5; (假命题)
② 若四边形为等腰梯形,则这个四边形的对角线相 等 . (真命题)
这里,命题①②都是省略了量词的全称量词命题.
有人认为,①的否定是“若x>1, 则 2x+ 1≤5”,
②的否定是“若四边形为等腰梯形,则这个四边形的对角 线不相等”.你认为对吗 如果不对,请你正确地写出命 题①②的否定.
谢谢
观看
第一章集合与常用 逻辑用语
1.5.2
全称量词命题和存在量 词命题的否定
科学家的自我否定
● 不久前,著名科学杂志自然发表了英国物理学家霍金
的一篇论文。他在文中提出,自己当初对世界的认识是有 缺陷的。按照经典理论,黑洞内部不会放过任何物质信息, 但最新理论却证明能量和信息能够逃离黑洞,这样,黑洞 是否真的存在就值得怀疑了
作为认识宇宙的重要突破,提出论证黑洞曾为,霍金
赢得世界声誉。质疑黑洞的存在,无疑对是对自己的否定。 这不是霍金第一次自我否定,两年前当一种与上帝粒子特 性一致的新粒子,希格斯粒子被发现时,霍金向她之前的, 打赌对象,预言上帝粒子存在的物理学家彼得希格斯寄去 一张100美元的支票,承认自己当年的无知。
· 霍金的自我否定并没有损害他在科学界的形象,反而赢 得了更多的掌声,同时也使他对宇宙的认识,更前进了一 步。
写出下列命题的否定:
(1)所有的矩形都是平行四边形;
(2)每一个素数都是奇数; (3) x ∈R,x +| x|≥0.
它们与原命题在形式上有什么变化
一个命题和它的否定
不能同时为真命题,也不 能同时为假命题,只能
一真一假.
探究一
命题的否定就是这个命题的反面
存在一个矩形不是平行四边形
(1) 所 有的矩形都是平行四边形的否定
存在
不是
(2)的否定是“并非每一个素数都是奇数”,
也就是说,
存在一个素数不是奇数;
(3)的否定是“并非所有的x∈R,x+|x|≥0 ”
也就是说,
3x∈R,x+|xl <0
·全称量词命题: Vx∈R,p (x),
·它的否定:3 x∈R,-p(x) .
·也就是说,全称量词命题的否定是存在量 词命题.
概念1
1.全称量词命题的否定一定是存在
量词命题吗
提 示 :是,因为全称量词的否定一定是存在 量词,所以全称量词命题的否定一定是存在量词 命题 .
2.用自然语言描述的全称量词
命题 的否定形式唯一吗
提 示 :不唯一,如“所有的菱形都是平行四 边形”,它的否定是“并不是所有的菱形都是平 行四边形”,也可以是“有些菱形不是平行四边 形” .
思考
例题讲解
例1写出下列全称量词命题的否定:
(1)所有能被3整除的整数都是奇数;
(2)每一个四边形的四个顶点在同一个圆上;
( 3 ) 对 任 意x ∈Z,x 的个位数字不等于3.
解 : (1)该命题的否定: 存在 一个能被3整除 的整数不是奇数.
(2)该命题的否定: 存 在一个四边形,它 的四个顶点不在同一个圆上.
(3)该命题的否定:3 x∈Z,x 的个位数字 等于3.
练习写出下列全称量词命题的否定,并判断真假: (1)Vx∈R,1-
(2)所有的正方形都是矩形.
(3)对任意x ∈Z,x 的个位数字不等于3.
(4)正数的绝对值是它本身.
解(1)该命题的 :3x∈R,1- (x>
R, ,所以- <0)
恒成立,所以这是一个假命题.
(2)该命题的否定:至少存在一个正方形不是矩形,
假命题.
(3)该命题的否定:至少存在一个x∈Z,x 的个位数
等于3,因为0 =0,1 =1,2 =4,3 =9,4 =16,
52=25,6 =36,72=49,82=64,92=81, …
所以这是一个假命题.
·
写出下列命题的否定:
(1)存在一个实数的绝对值是正数;
(2)有些平行四边形是菱形;
(3) 3x∈R,x —2x+3=0.
它们与原命题在形式上有什么变化
探究二
(1) 存在一个实数的绝对值是正数的否定
所有实数的绝对值都不是正数
命题的否定就是这个命题的反面
所有
不是
概念2
对含有一个量词的存在量词命题的否定, 有下面的结论:
存在量词命题:
3x∈R, -p(x)
它的否定:
Vx∈R,p(x)
也就是说,存在量词命题的否定是全称量 词命题.
原词 否定词 原词
否定词
等于 不等于 至多一个
至少两个
大于 不大于 至少一个
一个也没有
小于 不小于 任意
某个
是 不是 所有的
某些
都是 不都是
否定词总结
小结
1. 对全称命题否定的步骤
第一步改变量词:把全称量词换为恰当 的存在量词;
第二步否定性质:原命题中的“p(x)成立” 改为“非p(x)成立”。
2. 对存在性命题否定的步骤
第一步改变量词:把存在量词换为恰当 的全称量词;
第二步否定性质:原命题中的“p(x)成立” 改为“非p(x) 成立”。
练习
命题“3x∈R,x +2x+3=0”的否定是
【解析】因为存在量词命题的 否定是全称量词命题,所以命
题“3x ∈R,x +2x+3=0”
否定是“Vx∈R,
x2+2x+3≠0”
答案:Vx∈R,x +2x+3≠0
的
为什么存在量词命题的否定
一定是全称量词命题
提示:因为对“有的”,“存在 一个”,“至少一个”等词语的否定 是“都没有”,“都不存在”, “全 都不”等,所以存在量词命题的否定 一定是全称量词命题.
思考
“一般命题的否定”与“全称量词
命题和存在量词命题的否定”有
什么区别与联系
(1)一般命题的否定通常是保留条件否定其结论, 得到真假性完全相反的两个命题;全称量词命题和存 在量词命题的否定要在否定结论p(x)的同时,改变量 词的属性,即全称量词改为存在量词,存在量词改为 全称量词.
(2)与一般命题的否定相同,全称量词命题和 存在量词命题的否定的关键也是对关键词的否定.因 此,对全称量词命题和存在量词命题的否定,应根据 命题所叙述的对象的特征,挖掘其中的量词.全称量 词命题的否定与全称量词命题的真假性相反;存在量 词命题的否定与存在量词命题的真假性相反.
思考
练习
1. 写出下列命题的否定,并判断其真假.
(1)p: 所有的方程都有实数解;
(2)q:Vx∈R,4x —4x+1≥0;
(3)r:3x ∈R,x +2x +2≤0;
(4)s:某些平行四边形是菱形.
解 (1)非p: 存在一个方程没有实数解,真命 题.比如方程x +1=0 就没有实数解.
(2)非q:3x ∈R, 使 4x0(2)一4x +1<0, 假命 题 .这里由于Vx∈R,4x —4x+1=(2x—1) ≥0 恒成 立,是真命题,所以非q是假命题.
(3)非r:Vx∈R,x +2x+2>0, 真命题.
(4)非s: 每一个平行四边形都不是菱形,假命题。
2.把下列命题进行否定,并写在横线上.
(1)p:有些三角形是直角三角
(2)q: 所有的质数都是奇
(3)r所 有的所酌三角形都不是直角三角形
(4):有些实数的数愿数不是奇数
(3)有的人不睡觉
(4)所有实数的相反数都不比本身大
形 .
数.
觉 .
大.
练习
练习
3. 在本节,我们介绍了命题的否定的概念,知道一个命题 的否定仍是一个命题,它和原先的命题只能一真一假,不 能同真或同假.
在数学中,有很多“若p, 则q”形式的命题,有的是 真命题,有的是假命题.例如:
① 若x>1, 则 2x+1>5; (假命题)
② 若四边形为等腰梯形,则这个四边形的对角线相 等 . (真命题)
这里,命题①②都是省略了量词的全称量词命题.
有人认为,①的否定是“若x>1, 则 2x+ 1≤5”,
②的否定是“若四边形为等腰梯形,则这个四边形的对角 线不相等”.你认为对吗 如果不对,请你正确地写出命 题①②的否定.
谢谢
观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
