人教A版高中数学必修第一册 第5章 三角函数 课件(1)(共37张PPT)
文档属性
| 名称 | 人教A版高中数学必修第一册 第5章 三角函数 课件(1)(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 16:32:10 | ||
图片预览









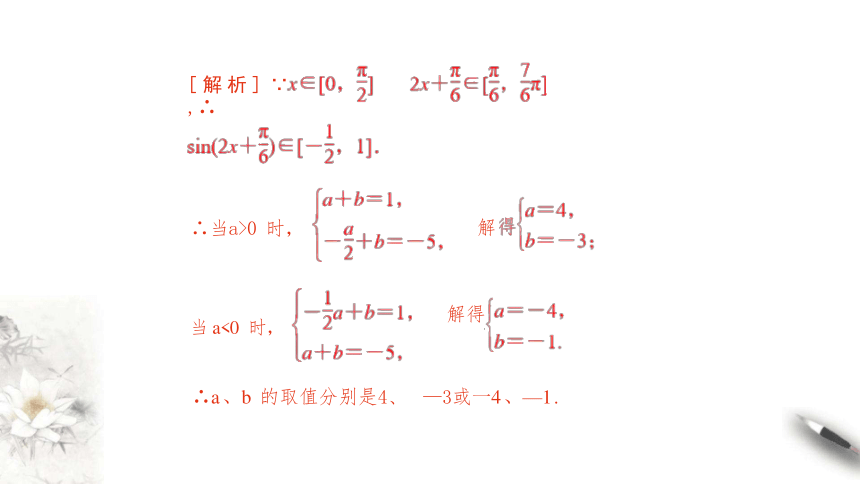
文档简介
(共37张PPT)
人教2019A版必修第一册
第五章 三角函数
小结与复习
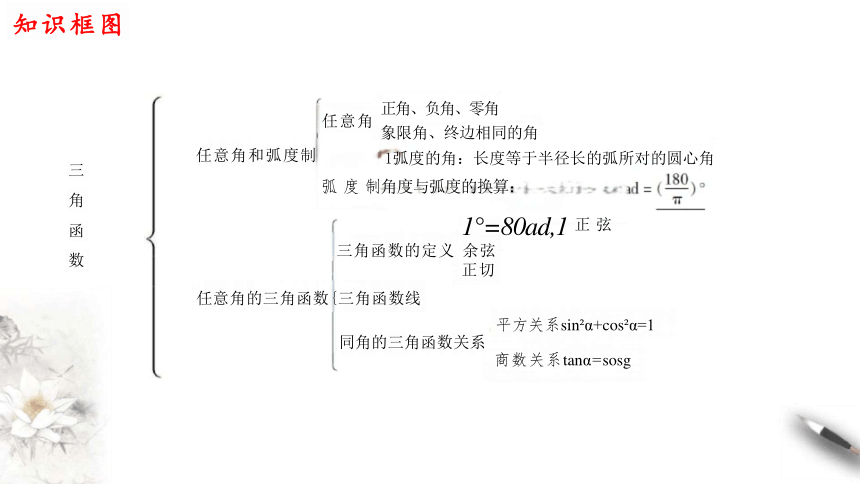
任意角的三角函数{三角函数线
平方关系sin α+cos α=1 同角的三角函数关系
商数关系tanα=sosg
弧 度 制角度与弧度的换算:1°=80ad,1 正 弦
三角函数的定义 余弦
正切
正角、负角、零角
象限角、终边相同的角
1弧度的角:长度等于半径长的弧所对的圆心角
任意角
任意角和弧度制
知识框图
三 角 函 数
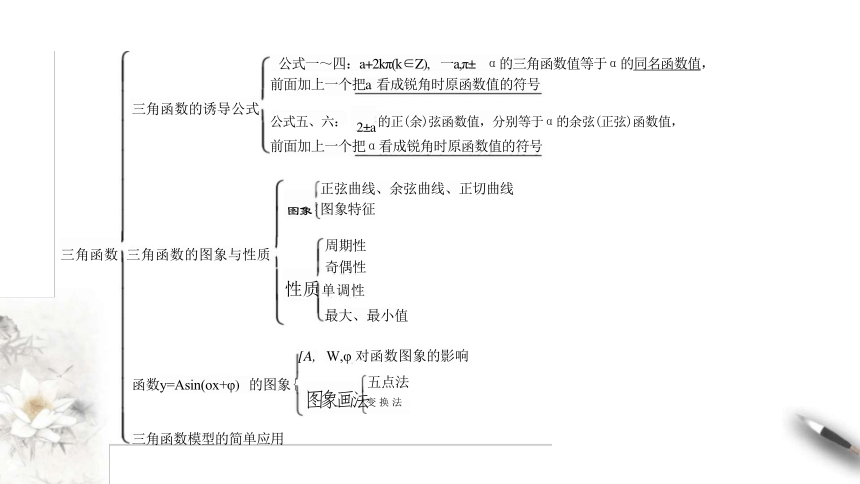
公式一~四:a+2kπ(k∈Z), 一a,π± α的三角函数值等于α的同名函数值,
前面加上一个把a 看成锐角时原函数值的符号
公式五、六: 2±a 的正(余)弦函数值,分别等于α的余弦(正弦)函数值,
前面加上一个把α看成锐角时原函数值的符号
[A, W,φ 对函数图象的影响
函数y=Asin(ox+φ) 的图象{ 五点法
三角函数模型的简单应用
周期性
奇偶性
性质单调性
最大、最小值
正弦曲线、余弦曲线、正切曲线
图象特征
三角函数 三角函数的图象与性质
图象画法变换法
三角函数的诱导公式
图象{
专题训练
专题一 正弦函数与余弦函数的对称性问题
正弦函数y=sinx, 余弦函数y=cosx, 在教材中已研究了
它们的定义域、值域、单调性、奇偶性、周期性.除了上述有 关内容之外,近年来有关正弦函数、余弦函数等对称性问题在 高考中有所出现,有必要对其作进一步的探讨.
函数y=sinx,x∈ R 的图象是中心对称图形,并且有无穷
多个对称中心,对称中心是图象与x 轴的任一交点,坐标为(kπ,
0)(k∈Z); 函 数y=cosx,x∈ R 的对称中心坐标为 0)(k
∈Z), 以上两个函数图象,也是轴对称图形,它们的对称轴分
别是x=kπ+z(k∈Z) 和x=kπ(k∈Z); 函 数y=tanx 的对称中心 坐标为 0)(k∈Z),,但它不是轴对称图形.
例题① 求 函 数 的对称中心和对称轴方程.
[分析] 利用三角函数的图象,把 看做一个变量,
用换元的方法求对称中心或对称轴方程,也可以考虑 y=sinx
的关系,利用变换的思想求对称轴与对称中
心 .
设
0),
则函数y=sinA 的对称中心为(kπ,
0),对称轴为x
的对称中心为
对称轴方程为
所以
即
少
重
[点拨] 本例中给出求三角函数的对称轴与对称中心的
两种方法,这都是解决三角问题的基本方法,要切实理解好.
专题二 三角函数的值域与最值问题
求三角函数的值域(最值)可分为几类:(1)是y=Asin(wx+
φ)+k 类型的,应利用其图象与性质、数形结合求解.(2)是可 化为以三角函数为元的二次函数类型,应确定三角函数的范 围,再用二次函数求解.(3)利用几何意义求解等.
为[一5,1],求a、b 的值.
[分析] 先 由x 的范围确定 的范围,再根据 a
的符号,讨论a 、b 的值 .
在 上的值域
例题 ②已知函数
解
解得
[ 解 析 ] ∵ ,∴
∴a 、b 的取值分别是4、 —3或一4 、—1 .
∴当a>0 时,
当 a<0 时,
,
[点拨] 本题是先由定义域确定正弦函数 的
值域,但对整个函数的最值的取得与a 有关系,故对a 进行分
类讨论.
例题③ 设a≥0, 若 y=cos x—asinx+b 的最大值为0,最
小值为一4,试求a 、b 的值 .
[分析] 通过换元化为一元二次函数最值问题求解.
由以上两式①②,得a=2,b=—2, 舍 a=—6 (与0≤a≤2
矛盾).
当0≤a≤2 时,
[解析] 原函数变形为
由以上两式③④,得a=2, 不 适 合a>2,∴ 应舍去 .
综上知,只有一组解
当 a>2 时,
[点拨] 一元二次函数区间最值问题含有参数时,应按照
对称轴与区间的相对位置去讨论.
专题三 三角函数的性质及应用
例题④若θ为第二象限角,试判断 的符号.
[分析] 确定符号,关键是确定每个因式的符号,而每个
因式的符号关键是看角所在的象限.
—1∴sin(cosθ)<0,cos(sin2θ)>0,∴
∴—1(1)求函数fi(x) 的表达式;
(2)将函数y=fi(x) 的图象向右平移 个单位,得函数y=f (x
的图象,求y=f (x) 的最大值,并求出此时自变量x 的集合 .
专题四 三角函数图象的平移及变换
例 题 5 函 数fi(x)=Asin(ox+φ)(A>0,w>0,
图象过点(0,1),如图所示.
的一段
[分析] 首先由图可确定周期 可得y
=Asinwx, 利用平移知识可知,图象对应的函数为y=Asino(x
[解析] (1)由图知,T=π, 于是 .将 y=Asin2x
的图象向左平移 ,得y=Asin2(x+12)=Asin(2x+6),∴
将(0,1)代入
当
即 时 ,ymax=2.
∴此时x 的值集合为 ,k∈Z}.
专题五三角函数式的化简
1. 三角函数式化简的基本原则:
(1)“切”化“弦”.
(2)异名化同名
(3)异角化同角.
(4)高次降幂.
(5)分式通分.
(6)无理化有理.
(7)常数的处理(特别注意“1”的代换).
2.三角函数式化简的基本技巧.
(1)sina,cosa→ 凑倍角公式.
(2)1±cosa→升幂公式.
(3)1±sina化为 再升幂或化
(4)asina+bcosa→辅助角公式 asina+bcosa=√a +b ·sin(a+
φ),其中 或asina+bcosα=√a +b cos(a-φ), 其中 tang
[特别提醒] 化简的基本思想方法是统一角、统一三角各个名
称 .
例 5 化简:
专题六 三角函数的求值
三角函数的求值有三种类型:
(1)给角求值: 一般所给的角都是非特殊角,要观察所给角与特殊角之间的关系,
利用三角变换消去非特殊角,转化为求特殊角的三角函数问题;(2)给值求值:
给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于
“变角”,如:a=(a+β) 一β,2a=(a+β)+(a —β)等.把所求角用含已知角的式
子表示,求解时要注意角范围的讨论;(3)给值求角:实质上是转化为“给值求
值”,关键也是变角,把所求角用含有已知角的式子表示,由所得的函数值结合该
函数的单调性求得角.
[探究] 利用β=(a+β)—α进行角的代换,则cosβ=cos[(a+
β)一a],利用公式展开,结合已知条件求解.
[解析] ∵a 、 β 均为锐角,∴0例6已知tana=43,
cosβ的值.
,a 、β
均为锐角,求
故cosβ=cos[(a+β)一a]
=cos(a+β)cosa+sin(a+β)sina
又tana=4√3,
1. 三角恒等式的证明问题主要有两种类型:不附加条件的恒
等式证明和条件恒等式证明.
(1)不附加条件的恒等式证明.
就是通过三角恒等变换,消除三角等式两端的差异,这是三角变
换的重要思想之一.证明的一般思路是由繁到简,如果两边都较 繁,则采用左右互推的思路,找一个桥梁过渡.
专题七 三角恒等式的证明
(2)条件恒等式的证明.
这类问题的解题思路是恰当、适时地使用条件,或仔细探求所给
条件与要证明的等式之间的内在联系,常用方法是代入法和消元 法 .
2. 证明三角恒等式常用的方法.
(1)从复杂的一边入手,逐步化简,证得与另一边相等;在证明过
程中,时刻“盯”住目标,分析其特征,时刻向着目标“奔”.
(2)从两边入手,证得等式两边都等于同一个式子.
(3)把要证的等式进行等价变形.
(4)作差法,证明其差为0.
例7求证:
[探究] 本题目中角有x 、4x, 函数名称有切、有弦.证明可
从左到右,或从右到左,统一角,统一函数名称.
原式得证.
[证明]
专题 八 三角恒等变换
三角恒等变换是三角函数的重要内容,搞清公式间的关系是
学习的关键.对于和、差角的三角函数公式,关键是弄清楚角的 变化,从整体上把握公式,既要学会正向运用,也要学会逆向运
用;对于倍、半角公式,可从a 与 之间的关系出发思考,通过这
种关系的思考而建立函数式之间的联系.对于和积互化公式,应
抓住公式特点进行变形,辅助角公式则是应用较为广泛的公式, 讨论三角函数的最值、周期、单调性等性质时,常使用此公式变 换 .
[探究] 将 f(x) 化成一角一函数的形式,再用y=Asin(wx+φ)
的性质作出解答.
(1)求 f(x)的最大值及最小正周期;
(2)若锐角α满足f(a)=3-2√3, 求
例 8 设f(x)=6cos x-√3sin2x.
的值.
故f(x)的最大值为2 √3+3;
最小正周期
又由
故
(2)由f(a)=3-2√3, 得
从而
解得
故
人教2019A版必修第一册
第五章 三角函数
小结与复习
任意角的三角函数{三角函数线
平方关系sin α+cos α=1 同角的三角函数关系
商数关系tanα=sosg
弧 度 制角度与弧度的换算:1°=80ad,1 正 弦
三角函数的定义 余弦
正切
正角、负角、零角
象限角、终边相同的角
1弧度的角:长度等于半径长的弧所对的圆心角
任意角
任意角和弧度制
知识框图
三 角 函 数
公式一~四:a+2kπ(k∈Z), 一a,π± α的三角函数值等于α的同名函数值,
前面加上一个把a 看成锐角时原函数值的符号
公式五、六: 2±a 的正(余)弦函数值,分别等于α的余弦(正弦)函数值,
前面加上一个把α看成锐角时原函数值的符号
[A, W,φ 对函数图象的影响
函数y=Asin(ox+φ) 的图象{ 五点法
三角函数模型的简单应用
周期性
奇偶性
性质单调性
最大、最小值
正弦曲线、余弦曲线、正切曲线
图象特征
三角函数 三角函数的图象与性质
图象画法变换法
三角函数的诱导公式
图象{
专题训练
专题一 正弦函数与余弦函数的对称性问题
正弦函数y=sinx, 余弦函数y=cosx, 在教材中已研究了
它们的定义域、值域、单调性、奇偶性、周期性.除了上述有 关内容之外,近年来有关正弦函数、余弦函数等对称性问题在 高考中有所出现,有必要对其作进一步的探讨.
函数y=sinx,x∈ R 的图象是中心对称图形,并且有无穷
多个对称中心,对称中心是图象与x 轴的任一交点,坐标为(kπ,
0)(k∈Z); 函 数y=cosx,x∈ R 的对称中心坐标为 0)(k
∈Z), 以上两个函数图象,也是轴对称图形,它们的对称轴分
别是x=kπ+z(k∈Z) 和x=kπ(k∈Z); 函 数y=tanx 的对称中心 坐标为 0)(k∈Z),,但它不是轴对称图形.
例题① 求 函 数 的对称中心和对称轴方程.
[分析] 利用三角函数的图象,把 看做一个变量,
用换元的方法求对称中心或对称轴方程,也可以考虑 y=sinx
的关系,利用变换的思想求对称轴与对称中
心 .
设
0),
则函数y=sinA 的对称中心为(kπ,
0),对称轴为x
的对称中心为
对称轴方程为
所以
即
少
重
[点拨] 本例中给出求三角函数的对称轴与对称中心的
两种方法,这都是解决三角问题的基本方法,要切实理解好.
专题二 三角函数的值域与最值问题
求三角函数的值域(最值)可分为几类:(1)是y=Asin(wx+
φ)+k 类型的,应利用其图象与性质、数形结合求解.(2)是可 化为以三角函数为元的二次函数类型,应确定三角函数的范 围,再用二次函数求解.(3)利用几何意义求解等.
为[一5,1],求a、b 的值.
[分析] 先 由x 的范围确定 的范围,再根据 a
的符号,讨论a 、b 的值 .
在 上的值域
例题 ②已知函数
解
解得
[ 解 析 ] ∵ ,∴
∴a 、b 的取值分别是4、 —3或一4 、—1 .
∴当a>0 时,
当 a<0 时,
,
[点拨] 本题是先由定义域确定正弦函数 的
值域,但对整个函数的最值的取得与a 有关系,故对a 进行分
类讨论.
例题③ 设a≥0, 若 y=cos x—asinx+b 的最大值为0,最
小值为一4,试求a 、b 的值 .
[分析] 通过换元化为一元二次函数最值问题求解.
由以上两式①②,得a=2,b=—2, 舍 a=—6 (与0≤a≤2
矛盾).
当0≤a≤2 时,
[解析] 原函数变形为
由以上两式③④,得a=2, 不 适 合a>2,∴ 应舍去 .
综上知,只有一组解
当 a>2 时,
[点拨] 一元二次函数区间最值问题含有参数时,应按照
对称轴与区间的相对位置去讨论.
专题三 三角函数的性质及应用
例题④若θ为第二象限角,试判断 的符号.
[分析] 确定符号,关键是确定每个因式的符号,而每个
因式的符号关键是看角所在的象限.
—1
∴—1
(2)将函数y=fi(x) 的图象向右平移 个单位,得函数y=f (x
的图象,求y=f (x) 的最大值,并求出此时自变量x 的集合 .
专题四 三角函数图象的平移及变换
例 题 5 函 数fi(x)=Asin(ox+φ)(A>0,w>0,
图象过点(0,1),如图所示.
的一段
[分析] 首先由图可确定周期 可得y
=Asinwx, 利用平移知识可知,图象对应的函数为y=Asino(x
[解析] (1)由图知,T=π, 于是 .将 y=Asin2x
的图象向左平移 ,得y=Asin2(x+12)=Asin(2x+6),∴
将(0,1)代入
当
即 时 ,ymax=2.
∴此时x 的值集合为 ,k∈Z}.
专题五三角函数式的化简
1. 三角函数式化简的基本原则:
(1)“切”化“弦”.
(2)异名化同名
(3)异角化同角.
(4)高次降幂.
(5)分式通分.
(6)无理化有理.
(7)常数的处理(特别注意“1”的代换).
2.三角函数式化简的基本技巧.
(1)sina,cosa→ 凑倍角公式.
(2)1±cosa→升幂公式.
(3)1±sina化为 再升幂或化
(4)asina+bcosa→辅助角公式 asina+bcosa=√a +b ·sin(a+
φ),其中 或asina+bcosα=√a +b cos(a-φ), 其中 tang
[特别提醒] 化简的基本思想方法是统一角、统一三角各个名
称 .
例 5 化简:
专题六 三角函数的求值
三角函数的求值有三种类型:
(1)给角求值: 一般所给的角都是非特殊角,要观察所给角与特殊角之间的关系,
利用三角变换消去非特殊角,转化为求特殊角的三角函数问题;(2)给值求值:
给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于
“变角”,如:a=(a+β) 一β,2a=(a+β)+(a —β)等.把所求角用含已知角的式
子表示,求解时要注意角范围的讨论;(3)给值求角:实质上是转化为“给值求
值”,关键也是变角,把所求角用含有已知角的式子表示,由所得的函数值结合该
函数的单调性求得角.
[探究] 利用β=(a+β)—α进行角的代换,则cosβ=cos[(a+
β)一a],利用公式展开,结合已知条件求解.
[解析] ∵a 、 β 均为锐角,∴0
cosβ的值.
,a 、β
均为锐角,求
故cosβ=cos[(a+β)一a]
=cos(a+β)cosa+sin(a+β)sina
又tana=4√3,
1. 三角恒等式的证明问题主要有两种类型:不附加条件的恒
等式证明和条件恒等式证明.
(1)不附加条件的恒等式证明.
就是通过三角恒等变换,消除三角等式两端的差异,这是三角变
换的重要思想之一.证明的一般思路是由繁到简,如果两边都较 繁,则采用左右互推的思路,找一个桥梁过渡.
专题七 三角恒等式的证明
(2)条件恒等式的证明.
这类问题的解题思路是恰当、适时地使用条件,或仔细探求所给
条件与要证明的等式之间的内在联系,常用方法是代入法和消元 法 .
2. 证明三角恒等式常用的方法.
(1)从复杂的一边入手,逐步化简,证得与另一边相等;在证明过
程中,时刻“盯”住目标,分析其特征,时刻向着目标“奔”.
(2)从两边入手,证得等式两边都等于同一个式子.
(3)把要证的等式进行等价变形.
(4)作差法,证明其差为0.
例7求证:
[探究] 本题目中角有x 、4x, 函数名称有切、有弦.证明可
从左到右,或从右到左,统一角,统一函数名称.
原式得证.
[证明]
专题 八 三角恒等变换
三角恒等变换是三角函数的重要内容,搞清公式间的关系是
学习的关键.对于和、差角的三角函数公式,关键是弄清楚角的 变化,从整体上把握公式,既要学会正向运用,也要学会逆向运
用;对于倍、半角公式,可从a 与 之间的关系出发思考,通过这
种关系的思考而建立函数式之间的联系.对于和积互化公式,应
抓住公式特点进行变形,辅助角公式则是应用较为广泛的公式, 讨论三角函数的最值、周期、单调性等性质时,常使用此公式变 换 .
[探究] 将 f(x) 化成一角一函数的形式,再用y=Asin(wx+φ)
的性质作出解答.
(1)求 f(x)的最大值及最小正周期;
(2)若锐角α满足f(a)=3-2√3, 求
例 8 设f(x)=6cos x-√3sin2x.
的值.
故f(x)的最大值为2 √3+3;
最小正周期
又由
故
(2)由f(a)=3-2√3, 得
从而
解得
故
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
