数学人教A版(2019)选择性必修第一册1.1.1空间向量及其运算 课件(共20张PPT)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.1.1空间向量及其运算 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 18:46:35 | ||
图片预览






文档简介
(共20张PPT)
高中数学 性必
选择
高中数学
1 空间向量的基本概念( 重 点 )
2 空间向量的线性运算( 重 点 )
空间 向量
共线、共面定理
01
空间向量的基本概念
一.空间向量的概念
章前图展示的是一个做滑翔伞运动的场景.
在滑翔过程中,飞行员会受到来自不同方向、大小各异的 力,例如绳索的拉力、风力、重力等,显然,这些力不在 同一个平面内.
类比的
方法
空间向量 平面向量
平面向量
一.空间向量的概念
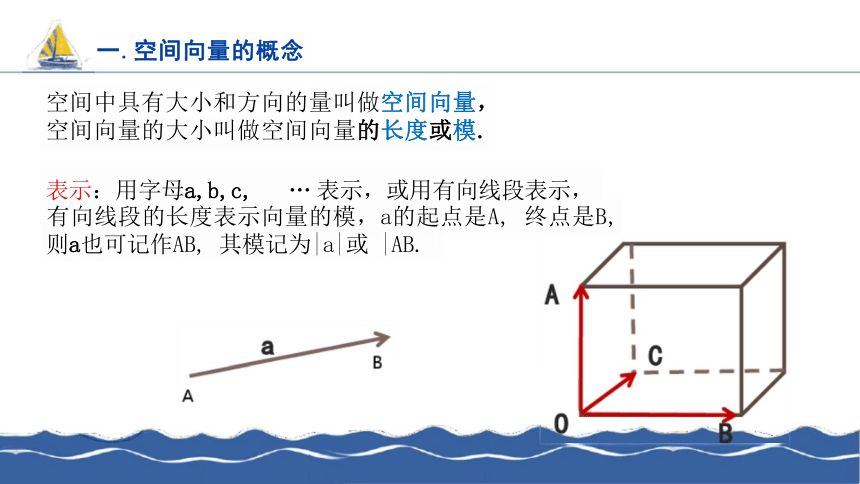
空间中具有大小和方向的量叫做空间向量,
空间向量的大小叫做空间向量的长度或模.
表示:用字母a,b,c, … 表示,或用有向线段表示,
有向线段的长度表示向量的模,a的起点是A, 终点是B,
则a也可记作AB, 其模记为|a|或 |AB.
一.空间向量的概念
特殊向量
零向量:规定长度为0的向量叫零向量, 记为0.
单位向量:模为1的向量叫单位向量. 相反向量:与向量a长度相等而方向相
反的向量,称为a的相反向 量,记为-a.
一.空间向量的概念
共线向量:如果表示若干空间向量的有向线段所在的直线互相平 行或重合,那么这些向量叫做共线向量或平行向量。
规定:零向量与任意向量平行,即对于任意向量a, 都有0//a
a b c
一.空间向量的概念
相等向量:方向相同且模相等的向量称为相等向量, 同向且等长的有向线段表示同一向量或相等向量.
空间向量是自由的,所以对于空间中的任意两个非零向量,我们都可以通过 平移使它们的起点重合.因为两条相交直线确定一个平面,所以起点重合的两个不 共线向量可以确定一个平面,也就是说,任意两个空问向量都可以平移到同一个
T rJ 1 w/2I T r H3r 的 1 I7 王 0
如 图,已知空间向量a,b , 以任意点O为起点,作向量OA=a,OB=b, 我
们就可以把它们平移到同一个平面a内 .
图1.1-3
a
结论:空间任意两个向量都可以平移到同一个平面内,所以 它们可用同一平面内的两条有向线段表示.
因此凡是涉及空间任意两个向量的问题,平面向量 中有关结论仍适用于它们
思考:空间中任意两个向量是否一定能够平移到同一
个平面内
B
一.空间向量的概念
3.(2022湖南长沙周南中学月考)如图所示,
在四棱柱的上底面ABCD中 ,AB=DC,则下
列向量相等的是 ( )
A.AD与CB B.0A与OC
C.AC与DB D.DO与OB
空间向量的线性运算
二.空间向量的线性运算
加减运算
在空间中,任意两个向量都可以平移到同一个平面 内,所以空间向量的加法和减法运算与平面向量相 同 .
(1)空间向量加法运算:
注:首尾顺次相接,起点指向终点
OC=OA+OB
OC=OA+AC
平行四边形法则:
三角形法则:
首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终 点的向量.
三角形法则推广
在空间中,任意两个向量都可以平 移到同一个平面内,所以空间向量的 加法和减法运算与平面向量相同.
(2)空间向量的减法运 算 :AB=OB-OA
注:起点相同,差向量为减向量终点指向被减向量的终点
二.空间向量的线性运算
数乘运算
实数λ与向量a的积是一个向量,这穗算叫向量的数乘
记作λa, 它的长度和方向规痴下:
(1)aa
(2)当λ>0时, λa的方向与的方向相同;
当λ<0时, λa的方向与的方向相反;
当λ=0时, λa=0.
向量的加、减、数乘运算统称向量的线性运算.
二.空间向量的线性运算
二.空间向量的线性运算
加法:三角形法则:a+ b= 0A+AB=OB;
平行四边形法则:a+b= 0A+Oc=OB;
减法:a-b= 0A-Oc=CA;
数乘运算:
运算律(λ,μeR):交换律:a+b=b+a
结合律:(a+b)+c=a+(b+c),λ(μa)=(λμ)a
分配律:(λ+μ)a=λa+μa,λ(a+b)=λa+λb
二.空间向量的线性运算
例 :已知平行六面体A BCD-A'B' C'D', 化简下
列向量表达式,并标出化简结果的向量:
(1)AB+BB +A'D
(2)AC -AC+BC
(1)AB+BB +A'D (2)ACi-AC+BC
=AB'+A'D' =CCi+BC
=AB'+B'Ci
=AC =BCi
练一练:
1.空间任意五个点A,B,C,D,E, 则DA+AE+CD-CB+EA 等于( )
A.DB B.AC C.AB D.BA
2.如图,在平行六面体ABCD-A B C D 中,E为A D 的中点,设AB=a,AD=b,AA =
c, 则CE=( )
二.空间向量的线性运算
名称 概念
记法
零向量 长度为0的向量
0
单位向量 模为1的向量
a|=1
相反向量 与向量a长度相等而方向相反的向量,叫做a的相反向量
-a
共线向量或 平行向量 相等向量 如果表示若干空间向量的有向线段所在的直线互相平 行或重合,那么这些向量叫做共线向量 方向相同且模相等的向量
a l b
a=b
小结:
小结:
加法:三角形法则:a+b = 0A+AB=OB;
平行四边形法则:a+b= 0A+Oc=OB;
减法:a-b= 0A-oc=CA;
数乘运算:
运算律(λ,μeR):交 换 律:a+b=b+a
结合律:(a+b)+c=a+(b+c),λ(μa)=(λμ)a
分配律:(λ+μ)a=λa+μa,λ(a+b)=λa+λb
高中数学 性必
选择
高中数学
1 空间向量的基本概念( 重 点 )
2 空间向量的线性运算( 重 点 )
空间 向量
共线、共面定理
01
空间向量的基本概念
一.空间向量的概念
章前图展示的是一个做滑翔伞运动的场景.
在滑翔过程中,飞行员会受到来自不同方向、大小各异的 力,例如绳索的拉力、风力、重力等,显然,这些力不在 同一个平面内.
类比的
方法
空间向量 平面向量
平面向量
一.空间向量的概念
空间中具有大小和方向的量叫做空间向量,
空间向量的大小叫做空间向量的长度或模.
表示:用字母a,b,c, … 表示,或用有向线段表示,
有向线段的长度表示向量的模,a的起点是A, 终点是B,
则a也可记作AB, 其模记为|a|或 |AB.
一.空间向量的概念
特殊向量
零向量:规定长度为0的向量叫零向量, 记为0.
单位向量:模为1的向量叫单位向量. 相反向量:与向量a长度相等而方向相
反的向量,称为a的相反向 量,记为-a.
一.空间向量的概念
共线向量:如果表示若干空间向量的有向线段所在的直线互相平 行或重合,那么这些向量叫做共线向量或平行向量。
规定:零向量与任意向量平行,即对于任意向量a, 都有0//a
a b c
一.空间向量的概念
相等向量:方向相同且模相等的向量称为相等向量, 同向且等长的有向线段表示同一向量或相等向量.
空间向量是自由的,所以对于空间中的任意两个非零向量,我们都可以通过 平移使它们的起点重合.因为两条相交直线确定一个平面,所以起点重合的两个不 共线向量可以确定一个平面,也就是说,任意两个空问向量都可以平移到同一个
T rJ 1 w/2I T r H3r 的 1 I7 王 0
如 图,已知空间向量a,b , 以任意点O为起点,作向量OA=a,OB=b, 我
们就可以把它们平移到同一个平面a内 .
图1.1-3
a
结论:空间任意两个向量都可以平移到同一个平面内,所以 它们可用同一平面内的两条有向线段表示.
因此凡是涉及空间任意两个向量的问题,平面向量 中有关结论仍适用于它们
思考:空间中任意两个向量是否一定能够平移到同一
个平面内
B
一.空间向量的概念
3.(2022湖南长沙周南中学月考)如图所示,
在四棱柱的上底面ABCD中 ,AB=DC,则下
列向量相等的是 ( )
A.AD与CB B.0A与OC
C.AC与DB D.DO与OB
空间向量的线性运算
二.空间向量的线性运算
加减运算
在空间中,任意两个向量都可以平移到同一个平面 内,所以空间向量的加法和减法运算与平面向量相 同 .
(1)空间向量加法运算:
注:首尾顺次相接,起点指向终点
OC=OA+OB
OC=OA+AC
平行四边形法则:
三角形法则:
首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终 点的向量.
三角形法则推广
在空间中,任意两个向量都可以平 移到同一个平面内,所以空间向量的 加法和减法运算与平面向量相同.
(2)空间向量的减法运 算 :AB=OB-OA
注:起点相同,差向量为减向量终点指向被减向量的终点
二.空间向量的线性运算
数乘运算
实数λ与向量a的积是一个向量,这穗算叫向量的数乘
记作λa, 它的长度和方向规痴下:
(1)aa
(2)当λ>0时, λa的方向与的方向相同;
当λ<0时, λa的方向与的方向相反;
当λ=0时, λa=0.
向量的加、减、数乘运算统称向量的线性运算.
二.空间向量的线性运算
二.空间向量的线性运算
加法:三角形法则:a+ b= 0A+AB=OB;
平行四边形法则:a+b= 0A+Oc=OB;
减法:a-b= 0A-Oc=CA;
数乘运算:
运算律(λ,μeR):交换律:a+b=b+a
结合律:(a+b)+c=a+(b+c),λ(μa)=(λμ)a
分配律:(λ+μ)a=λa+μa,λ(a+b)=λa+λb
二.空间向量的线性运算
例 :已知平行六面体A BCD-A'B' C'D', 化简下
列向量表达式,并标出化简结果的向量:
(1)AB+BB +A'D
(2)AC -AC+BC
(1)AB+BB +A'D (2)ACi-AC+BC
=AB'+A'D' =CCi+BC
=AB'+B'Ci
=AC =BCi
练一练:
1.空间任意五个点A,B,C,D,E, 则DA+AE+CD-CB+EA 等于( )
A.DB B.AC C.AB D.BA
2.如图,在平行六面体ABCD-A B C D 中,E为A D 的中点,设AB=a,AD=b,AA =
c, 则CE=( )
二.空间向量的线性运算
名称 概念
记法
零向量 长度为0的向量
0
单位向量 模为1的向量
a|=1
相反向量 与向量a长度相等而方向相反的向量,叫做a的相反向量
-a
共线向量或 平行向量 相等向量 如果表示若干空间向量的有向线段所在的直线互相平 行或重合,那么这些向量叫做共线向量 方向相同且模相等的向量
a l b
a=b
小结:
小结:
加法:三角形法则:a+b = 0A+AB=OB;
平行四边形法则:a+b= 0A+Oc=OB;
减法:a-b= 0A-oc=CA;
数乘运算:
运算律(λ,μeR):交 换 律:a+b=b+a
结合律:(a+b)+c=a+(b+c),λ(μa)=(λμ)a
分配律:(λ+μ)a=λa+μa,λ(a+b)=λa+λb
