新教材高中数学人教A版选择性必修一 椭圆及其标准方程 课件(共24张PPT)
文档属性
| 名称 | 新教材高中数学人教A版选择性必修一 椭圆及其标准方程 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 20:12:05 | ||
图片预览






文档简介
(共24张PPT)
第三章圆锥曲线的方程 3.1椭圆
3.1.1 椭圆及其标准方程
人教A 版2019 选择性必修第一册
我们的太阳系
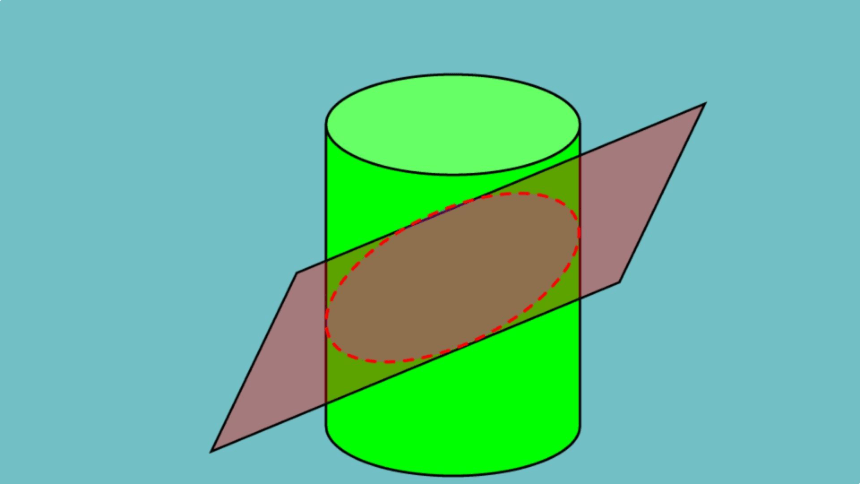
我们知道,用一个垂直于圆锥的轴的平面截 圆锥,截口曲线(截面与圆锥侧面的交线) 是一个圆.如果改变圆锥的轴与截平面所成 的角,那么会得到怎样的曲线呢
如图,用一个不垂直于圆锥的轴的平面截圆 锥,当圆锥的轴与截面所成的角不同时,可 以得到不同的截口曲线,它们分别是椭圆、
抛物线和双曲线.我们通常把椭圆、抛物线、 双曲线统称为圆锥曲线 (conicsections).
圆
双曲线
抛物线
椭 圆
圆锥曲线与科研、生产以及人类生活有着紧密的关系.如行星绕太阳运 行的轨道是椭圆,发电厂冷却塔的外形线是双曲线,探照灯反射镜面、 卫星接收天线是抛物线绕其对称轴旋转所成的抛物面....为什么圆锥曲 线有如此广泛的应用呢 我们可以从它们的几何特征及其性质中找到答 案 .
圆锥曲线的发现与研究始于古希腊.当时人们用纯几何的方法研究这些 与圆密切相关的曲线,它们的几何性质是圆的几何性质的自然推广.17 世纪,笛卡儿发明了坐标系,人们开始借助坐标系,运用代数方法研究 圆锥曲线.
本章我们继续采用坐标法,在探究圆锥曲线几何特征的基础上,建立它 们的方程,通过方程研究它们的性质,并解决与圆锥曲线有关的几何问 题和实际问题,进一步感受数形结合的思想方法,体会坐标法的魅力与
威力.
椭圆是圆锥曲线的一种,具有丰富的几何性质,在科研、生产和人类生 活中具有广泛的应用.那么,椭圆到底有怎样的几何特征 我们该如何 利用这些特征建立椭圆的方程,从而为研究椭圆的几何性质奠定基础
一
探究
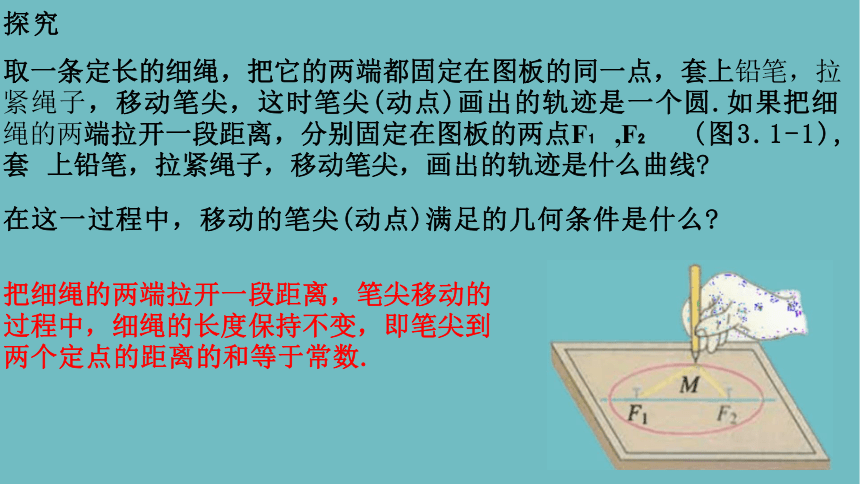
取一条定长的细绳,把它的两端都固定在图板的同一点,套上铅笔,拉 紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个圆.如果把细 绳的两端拉开一段距离,分别固定在图板的两点F ,F (图3.1-1),套 上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线
在这一过程中,移动的笔尖(动点)满足的几何条件是什么
把细绳的两端拉开一段距离,笔尖移动的 过程中,细绳的长度保持不变,即笔尖到 两个定点的距离的和等于常数.
我们把平面内与两个定点F1,F 的距离的和等于常数(大于|F F )的 点
的轨迹叫做椭圆(ellipse).
这两个定点叫做椭圆的焦点(focus),
两焦点间的距离叫做椭圆的焦距(focusdistance),
焦距的一半称为半焦距.
由椭圆的定义可知,
上述移动的笔尖(动点)画出的轨迹是椭圆.
思考
观察椭圆的形状,你认为怎样建立坐标系可能使所得的椭圆方程形式简 单
观察我们画出的图形,可以发现椭圆具有对称性,
而且过两个焦点的直线是它的对称轴,所以我们
以经过椭圆两焦点F ,F 的直线为x轴,线段F ,F
的垂直平分线为y轴,建立平面直角坐标系,
如图3.1-2所示.
图3.1-2
设M(x,y) 是椭圆上任意一点,椭圆的焦距为2c(c>0),那么焦点F ,F 的
坐标分别为(-c,0),(c,0).根据椭圆的定义,设点M 与焦点F ,F 的距离的
和等于2a. 设为2a能为问题研究带来方便.
由椭圆的定义可知,椭圆可看作点集P={M||MF |+|MF |=2a}.
因为|MF |= √ (x+c) +y ,MF |= √ (x-c) +y .
所以√(x+c) +y +√(x-c) +y =2a. ①
为了化简方程①,我们将其左边的一个根式移到右边,得
√(x+c) +y =2a-√(x-c) +y ②
对方程②两边平方,得
(x+c) +y =4a -4aJ(x-c) +y +(x-c) +y
整理,得a -cx=a √ (x-c) +y ③
对方程③两边平方,得a -2a cx+c x =a x -2a cx+a c +a y ,
整理,得(a -c )x +a y =a (a -c ) ④
将方程④两边同除以a (a -c ),得 ⑤
由椭圆的定义可知,2a>2c>0, 即a>c>0, 所以a -c >0.
思考
观察图3.1-3,你能从中找出表示a,c,Ja -c 的线段吗
由图3.1-3可知,PF |=|PF |=a,OF |=|OF I=c,|PO|= √a -c .
令b=|PO= √a -c , 那么方程⑤就是
图3.1-3
由于方程②③的两边都是非负实数,因此方程①到方程⑥的变形都是
同解变形.这样,椭圆上任意一点的坐标(x,y) 都满足方程⑥;
反之,以方程⑥的解为坐标的点(x,y) 与椭圆的两个焦点(c,0),(-c,0)的
距离之和为2a,即以方程⑥的解为坐标的点都在椭圆上.
我们称方程⑥是椭圆的方程,这个方程叫做椭圆的标准方程.它表示焦
点 在x轴上,两个焦点分别是F (-c,0),F (c,0)的椭圆,这 里c =a - b .
思 考
如图3.1-4,如果焦点F ,F 在y轴上,且F ,F 的坐标分别为(0,-c),(0,c),
a,b的意义同上,那么椭圆的方程是什么
容易知道,此时椭圆的方程是
这个方程也是椭圆的标准方程.
图3.1-4
例1已知椭圆的两个焦点坐标分别是(-2,0),(2,0),并且经过点
求它的标准方程.
解:由于椭圆的焦点在x轴上,所以设它的标准方程为
由椭圆的定义知(=2
所以a=√ 10.b =a -c =10-4=6,
所以所求椭圆的标准方程为
你还能用其他方法求它的标准方程吗 试比较不同方法的特点.
解法二:由于椭圆的焦点在x轴上,
所以设它的标准方程为
由椭圆的定义知c=2, 所以a =b +c =b +4, 所以
将 代入,得 整理得2b -9b -18=0,
∴(2b +3)(b -6)=0, 解得b =6,:a =b +4=10,
所以所求椭圆的标准方程为
例2如图3.1-5,在圆x +y =4 上任取一点P,过点P作x轴的垂线段PD,
D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹是什么 为什么
分析:点P在圆x +y =4 上运动,点P的运动
引起点M 运动.我们可以由M 为线段PD 的中
点得到点M与点P坐标之间的关系式,并由
点P的坐标满足圆的方程得到点M 的坐标
所满足的方程.
图3.1-5
解:设点M 的坐标为(x,y),点P的坐标为(x ,y ),则点D的坐标为(x ,0),
由点M 是线段PD的中点,
因为点在圆x +y =4 上,所以x +y =4 ①
把x,=x,y,=2y 代入方程①,得x +4y =4,
即 . 所以点M 的轨迹是椭圆
寻求点M 的坐标(x,y)中x,y与x ,y 之间的关系,
然后消去x ,y ,得到点M 的轨迹方程。这是解
析几何中求点的轨迹方程常用的方法.利用
信息技术,可以更方便地探究点M的轨迹的形状.
●
思考
由例2我们发现,可以由圆通过“压缩”得到椭圆.你能由圆通过“拉
伸”得到椭圆吗 如何“拉伸” 由此你能发现椭圆与圆之间的关系吗
例3如图3.1-6,设A,B两点的坐标分别为(-5,0),(5,0).直线AM,BM 相
交于点M, 且它们的斜率之积是 ,求点M的轨迹方程.
分析:设点M 的坐标为(x,y),那么直线AM,BM 的斜率就可用含x,y的
关系式分别表示.由直线AM,BM 的斜率
图3.1-6之积是 可得出x,y之间的关
系式,进而得到点M的轨迹方程.
图3.1-6
所以直线AM的斜率k
同理,直线BM 的斜率人 由已知,有
化简,得点M的轨迹方程为
解:设点M 的坐标为(x,y),因为点A的坐标是(-5,0),
点M 的轨迹是除去(-5,0),(5,0)两点的椭圆.
图3.1-6
● ●
特殊情况,当b=a 时,c=0, 此时
直径所对的圆周角是直角
结论:已知椭圆方程为
为椭圆上任一点,则
椭圆的第三定义
●
推广:已知椭圆方程为
对称的两点,P(x,y) 为椭圆上任一点,则
,点4,B是椭圆上关于原点
第三章圆锥曲线的方程 3.1椭圆
3.1.1 椭圆及其标准方程
人教A 版2019 选择性必修第一册
我们的太阳系
我们知道,用一个垂直于圆锥的轴的平面截 圆锥,截口曲线(截面与圆锥侧面的交线) 是一个圆.如果改变圆锥的轴与截平面所成 的角,那么会得到怎样的曲线呢
如图,用一个不垂直于圆锥的轴的平面截圆 锥,当圆锥的轴与截面所成的角不同时,可 以得到不同的截口曲线,它们分别是椭圆、
抛物线和双曲线.我们通常把椭圆、抛物线、 双曲线统称为圆锥曲线 (conicsections).
圆
双曲线
抛物线
椭 圆
圆锥曲线与科研、生产以及人类生活有着紧密的关系.如行星绕太阳运 行的轨道是椭圆,发电厂冷却塔的外形线是双曲线,探照灯反射镜面、 卫星接收天线是抛物线绕其对称轴旋转所成的抛物面....为什么圆锥曲 线有如此广泛的应用呢 我们可以从它们的几何特征及其性质中找到答 案 .
圆锥曲线的发现与研究始于古希腊.当时人们用纯几何的方法研究这些 与圆密切相关的曲线,它们的几何性质是圆的几何性质的自然推广.17 世纪,笛卡儿发明了坐标系,人们开始借助坐标系,运用代数方法研究 圆锥曲线.
本章我们继续采用坐标法,在探究圆锥曲线几何特征的基础上,建立它 们的方程,通过方程研究它们的性质,并解决与圆锥曲线有关的几何问 题和实际问题,进一步感受数形结合的思想方法,体会坐标法的魅力与
威力.
椭圆是圆锥曲线的一种,具有丰富的几何性质,在科研、生产和人类生 活中具有广泛的应用.那么,椭圆到底有怎样的几何特征 我们该如何 利用这些特征建立椭圆的方程,从而为研究椭圆的几何性质奠定基础
一
探究
取一条定长的细绳,把它的两端都固定在图板的同一点,套上铅笔,拉 紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个圆.如果把细 绳的两端拉开一段距离,分别固定在图板的两点F ,F (图3.1-1),套 上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线
在这一过程中,移动的笔尖(动点)满足的几何条件是什么
把细绳的两端拉开一段距离,笔尖移动的 过程中,细绳的长度保持不变,即笔尖到 两个定点的距离的和等于常数.
我们把平面内与两个定点F1,F 的距离的和等于常数(大于|F F )的 点
的轨迹叫做椭圆(ellipse).
这两个定点叫做椭圆的焦点(focus),
两焦点间的距离叫做椭圆的焦距(focusdistance),
焦距的一半称为半焦距.
由椭圆的定义可知,
上述移动的笔尖(动点)画出的轨迹是椭圆.
思考
观察椭圆的形状,你认为怎样建立坐标系可能使所得的椭圆方程形式简 单
观察我们画出的图形,可以发现椭圆具有对称性,
而且过两个焦点的直线是它的对称轴,所以我们
以经过椭圆两焦点F ,F 的直线为x轴,线段F ,F
的垂直平分线为y轴,建立平面直角坐标系,
如图3.1-2所示.
图3.1-2
设M(x,y) 是椭圆上任意一点,椭圆的焦距为2c(c>0),那么焦点F ,F 的
坐标分别为(-c,0),(c,0).根据椭圆的定义,设点M 与焦点F ,F 的距离的
和等于2a. 设为2a能为问题研究带来方便.
由椭圆的定义可知,椭圆可看作点集P={M||MF |+|MF |=2a}.
因为|MF |= √ (x+c) +y ,MF |= √ (x-c) +y .
所以√(x+c) +y +√(x-c) +y =2a. ①
为了化简方程①,我们将其左边的一个根式移到右边,得
√(x+c) +y =2a-√(x-c) +y ②
对方程②两边平方,得
(x+c) +y =4a -4aJ(x-c) +y +(x-c) +y
整理,得a -cx=a √ (x-c) +y ③
对方程③两边平方,得a -2a cx+c x =a x -2a cx+a c +a y ,
整理,得(a -c )x +a y =a (a -c ) ④
将方程④两边同除以a (a -c ),得 ⑤
由椭圆的定义可知,2a>2c>0, 即a>c>0, 所以a -c >0.
思考
观察图3.1-3,你能从中找出表示a,c,Ja -c 的线段吗
由图3.1-3可知,PF |=|PF |=a,OF |=|OF I=c,|PO|= √a -c .
令b=|PO= √a -c , 那么方程⑤就是
图3.1-3
由于方程②③的两边都是非负实数,因此方程①到方程⑥的变形都是
同解变形.这样,椭圆上任意一点的坐标(x,y) 都满足方程⑥;
反之,以方程⑥的解为坐标的点(x,y) 与椭圆的两个焦点(c,0),(-c,0)的
距离之和为2a,即以方程⑥的解为坐标的点都在椭圆上.
我们称方程⑥是椭圆的方程,这个方程叫做椭圆的标准方程.它表示焦
点 在x轴上,两个焦点分别是F (-c,0),F (c,0)的椭圆,这 里c =a - b .
思 考
如图3.1-4,如果焦点F ,F 在y轴上,且F ,F 的坐标分别为(0,-c),(0,c),
a,b的意义同上,那么椭圆的方程是什么
容易知道,此时椭圆的方程是
这个方程也是椭圆的标准方程.
图3.1-4
例1已知椭圆的两个焦点坐标分别是(-2,0),(2,0),并且经过点
求它的标准方程.
解:由于椭圆的焦点在x轴上,所以设它的标准方程为
由椭圆的定义知(=2
所以a=√ 10.b =a -c =10-4=6,
所以所求椭圆的标准方程为
你还能用其他方法求它的标准方程吗 试比较不同方法的特点.
解法二:由于椭圆的焦点在x轴上,
所以设它的标准方程为
由椭圆的定义知c=2, 所以a =b +c =b +4, 所以
将 代入,得 整理得2b -9b -18=0,
∴(2b +3)(b -6)=0, 解得b =6,:a =b +4=10,
所以所求椭圆的标准方程为
例2如图3.1-5,在圆x +y =4 上任取一点P,过点P作x轴的垂线段PD,
D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹是什么 为什么
分析:点P在圆x +y =4 上运动,点P的运动
引起点M 运动.我们可以由M 为线段PD 的中
点得到点M与点P坐标之间的关系式,并由
点P的坐标满足圆的方程得到点M 的坐标
所满足的方程.
图3.1-5
解:设点M 的坐标为(x,y),点P的坐标为(x ,y ),则点D的坐标为(x ,0),
由点M 是线段PD的中点,
因为点在圆x +y =4 上,所以x +y =4 ①
把x,=x,y,=2y 代入方程①,得x +4y =4,
即 . 所以点M 的轨迹是椭圆
寻求点M 的坐标(x,y)中x,y与x ,y 之间的关系,
然后消去x ,y ,得到点M 的轨迹方程。这是解
析几何中求点的轨迹方程常用的方法.利用
信息技术,可以更方便地探究点M的轨迹的形状.
●
思考
由例2我们发现,可以由圆通过“压缩”得到椭圆.你能由圆通过“拉
伸”得到椭圆吗 如何“拉伸” 由此你能发现椭圆与圆之间的关系吗
例3如图3.1-6,设A,B两点的坐标分别为(-5,0),(5,0).直线AM,BM 相
交于点M, 且它们的斜率之积是 ,求点M的轨迹方程.
分析:设点M 的坐标为(x,y),那么直线AM,BM 的斜率就可用含x,y的
关系式分别表示.由直线AM,BM 的斜率
图3.1-6之积是 可得出x,y之间的关
系式,进而得到点M的轨迹方程.
图3.1-6
所以直线AM的斜率k
同理,直线BM 的斜率人 由已知,有
化简,得点M的轨迹方程为
解:设点M 的坐标为(x,y),因为点A的坐标是(-5,0),
点M 的轨迹是除去(-5,0),(5,0)两点的椭圆.
图3.1-6
● ●
特殊情况,当b=a 时,c=0, 此时
直径所对的圆周角是直角
结论:已知椭圆方程为
为椭圆上任一点,则
椭圆的第三定义
●
推广:已知椭圆方程为
对称的两点,P(x,y) 为椭圆上任一点,则
,点4,B是椭圆上关于原点
