2.3 一元二次不等式及其解法 课件(共30张PPT) 高中数学人教版(A版)必修 第一册
文档属性
| 名称 | 2.3 一元二次不等式及其解法 课件(共30张PPT) 高中数学人教版(A版)必修 第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
一元二次不等式及其解法
一、课前小练
(一)判一判(对的打“ √ ”,错的打“×”)
(1)若不等式 ax +bx+c<0 的解集为(x ,x ),则必有a>0.( √)
(2)若方程ax +bx+c=0(a≠0) 没有实数根,则不等式ax +bx
十c>0的解集为R. (×)
(3)若二次函数y=ax +bx+c 的图象开口向下,则不等式 ax
十bx+c<0 的解集一定不是空集. ( √)
所以不等式2x —x—3>0的解集 故选B.
答案:B
(二)选一选
1. 不等式2x —x—3>0的解集为
B.
解析:由2x —x—3=(2x—3)(x+1)>0,得
x<—1,
( )
2. 若集合M={xlx +5x—14<0},N={xl1于 ( )
A.0 B.(1,4)
C.(2,4) D.(1,2)
解析:因为M={xlx +5x—14<0}={xl(x—2)·(x+7)<0}=
{xl—7答案:D
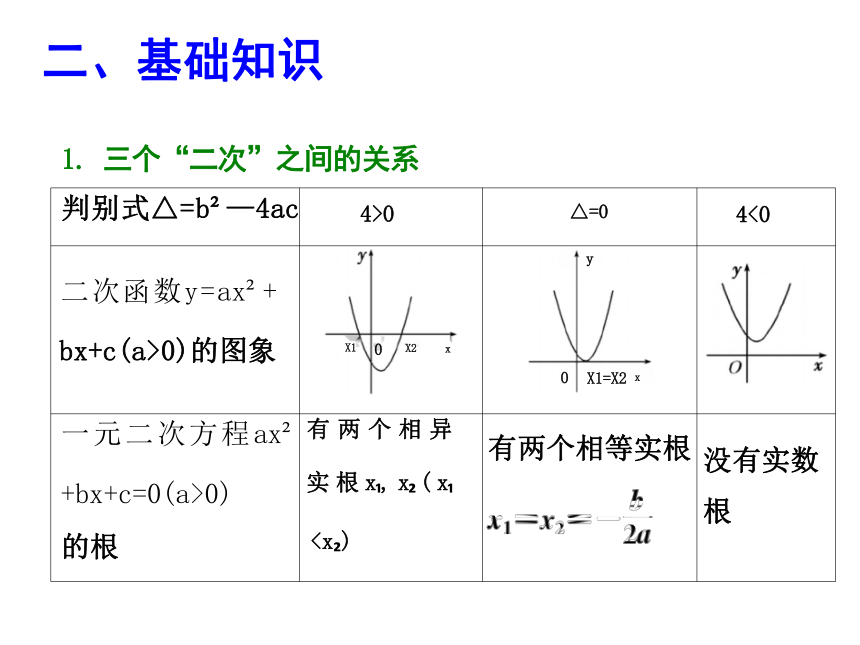
判别式△=b —4ac 4>0 △=0
4<0
二次函数y=ax + bx+c(a>0)的图象 X1 0 X2 x y 0 X1=X2 x
一元二次方程ax +bx+c=0(a>0) 的根 有 两 个 相 异 实 根 x , x ( x没有实数
根
二、基础知识
1. 三个“二次”之间的关系
判别式 4= 4>0 4=0
4<0
一元二次不等式 ax + >0)的解集 {xlxx }
R
一元二次不等式 ax >0)的解集 {x|x2.一元二次不等式的解法步骤
(1)将不等式化为右边为零,左边为二
次项系数大于零的不等式 ax +bx
十c>0(a>0)或 ax +bx+c<0(a>0).
(2)求出相应的一元二次方程的根.
在不等式 ax +bx+
c>0(a≠0) 中,如果二
次项系数 a<0, 可 根 据不等式的性质,将 其转化为正数.
开口向上的二次不等式的解法顺口溜:
大于取两边,小于取中间.
(3)利用二次函数的图象与x 轴的交点确定一元二次不等式的
解集.
3.一元二次不等式恒成立问题
(1)不等式ax +bx+c>0(a≠0),x∈R 恒成立→a>0 且4<0;
(2)不等式 ax +bx+c<0(a≠0),x∈R 恒成立 a<0 且4<0;
(3)若a 可以为0,需要分类讨论, 一般优先考虑a=0 的
情形.
考点一一元二次不等式的解法
三、典型例题分析
考法(一)不含参数的一元二次不等式
[典例] 解下列不等式:(1)—3x —2x+8≥0;
(2)0[解]( 1)原不等式可化为3x +2x—8≤0,
即(3x—4)(x+2)≤0, 解 得
所以原不等式的解集
(2)原不等式等价
0
,
借助于数轴,如图所示, 原不等式的解集为{xl—2≤x<一1或2把不等式变形为二次项系数大于零的标准形式
计算对应方程的判别式
求出对应的一元二次方程的根,或根据判别式说明
方程有没有实根
利用“大于取两边,小于取中间”写出不等式的解集
[解题技法]
解一元二次不等式的4个步骤
判 求 写
变 —
考法(二)含参数的一元二次不等式
[典例] 解不等式ax —(a+1)x+1<0(a>0).
[解] 原不等式变为(ax—1)(x—1)<0,
因 为a>0, 所 以
所以当a>1, 时,解
当 a=1 时,解集为o; 当 0综上,当0当a=1 时,不等式的解集为o;
当a>1 时,不等式的解集为
[解题技法]
1. 解含参数的一元二次不等式的步骤
(1)若二次项系数含有参数,则应讨论参数是等于0,小于
0 , 还是大于0,然后将不等式转化为二次项系数为正的形式;
(2)判断方程根的个数,讨论判别式△与0的关系;
(3)确定无根时可直接写出解集;确定方程有两个根时,要
讨论两根的大小关系,从而确定不等式的解集.
以(2x+9)(x—1)≤0, 解 得 所以不等式(x+5)(3—
2x)≥6 的解集 .故选D.
答案: D
[题组训练]
1.不 等 式(x+5)(3—2x)≥6 的解集是
解析:不等式(x+5)(3—2x)≥6 可 化 为 2
( )
2. 已知不等式ax —bx—1≥0 的解集是 则不等式
x —bx—a<0 的解集是 ( )
A.(2,3) B. ( 一 , 2 )U(3, 十 一)
C.
解析:由题意知 ,-3是方程ax —bx—1=0的两根,
所以由根与系数的关系
解 不等式x —bx—a<0 即为x —5x+6<0,
解集为(2,3). 答案:A
3. 求不等式12x —ax>a (a∈R)的解集.
解:原不等式可化为12x —ax—a >0,
即(4x+a)(3x—a)>0,
令(4x+a)(3x—a)=0, 解 得 ●
当a>0 时,不等式的解集
当a=0 时,不等式的解集为(一0,0)U(0, 十一);
当a<0 时,不等式的解集为
考点二绝对值不等式
和分式不等式
考法(一)含绝对值不等式的解法
【典例】解下列不等式:
(1)|2x-1≥3(2)|2x-1≥3x-1
(1)解法1:由|2x-1≥3 得2x-1≥3 或2x-1≤-3
故x≥2 或x≤-1:. 解集为{x|x≥2 或x≤-1}
(1)解法2:由|2x-1≥3 得(2x-1) ≥9
故4x -4x-8≥0:. 解集为{x|x≥2 或x≤-1}
(2)解:由|2x-1≥3x-1| 得(2x-1) ≥3x-1|
故5x -2x≤0:解集为{x|0≤x≤
解题技法:解绝对值不等式的一般步骤是:(1)解对应的
方程;(2)把根从小到大排列;(3)利用“大于取两边,
小于取中间”的原则去取解集.特别地,若两边都有
绝对值,则可两边同时平方求解集.
题组训练
(1)|3x-2<4(2)|2x-1≥3x-1
(2)解集为{x|x≤3
(1)解法1:由
∴{x| 或x<-3}
(1)解法2:由
·
:
考法(二)分式不等式的解法
【典例】解下列不等式:
解题技法:解分式不等式的一般步骤是:先移项
(必须把所有的项都移到同一边),再通分;
题组训练:
1-2<-x的解集为
解集为{x|x<-2 或0考点三 一元二次不等式恒成立
问题
考法(一) 在 R 上的恒成立问题
[典例]若不等式(a—2)x +2(a—2)x—4<0 对一切 x∈R 恒成
立,则实数a 的取值范围是 ( )
A. ( 一 , 2 ) B.[—2,2] C.(—2,2) D.(—,—2)
[解析] 当 a—2=0, 即 a=2 时,不等式为一4<0,对一切x ∈R
恒成立.
当a≠2 时,贝
解得—2[答案] C
日只
[解题技法] 一元二次不等式恒成立的条件
(1)ax +bx+c>0(a≠0)恒成立的充要条件
(2)ax +bx+c<0(a≠0)恒成立的充要条件
考法(二)在给定区间上的恒成立问题
[典例] 若对任意的x∈[—1,2], 都有
常数),则a 的取值范围是 ( )
A. [ 一 0 , — 3 ] B. ( 一 0 , 0 )
C.[1,十 0 ] D. ( 一 0 , 1 )
[解析] 法一:令 f(x)=x —2x+a, 则由题意,得
法二:当x∈[—1,2]时,不等式x —2x+a≤0恒成立等价于a≤
—x +2x恒成立,则由题意,得a≤(—x +2x)min(x∈[-1,2]).而 —x +2x=—(x—1) +1, 则 当x=—1 时,(—x +2x)min=—3, 所
以 a≤—3, 故 选A. [答案] A
f(一1)=(一1) -2×(一1)+a≤0, f(2)=2 -2×2+a≤0,
解得a≤—3, 故选A.
[解题技法]
一元二次不等式在给定区间上的恒成立问题的求解方法
(1)直接转化为最值问题求解:
f(x)≥0 恒成立→f(x)min≥0;
f(x)≤0恒成立→f(x)max≤0.
(2)先分离变量,再转化为最值问题求解:
f(x)≥a恒成立→f(x)min≥a;
f(x)≤a 恒成立→f(x)max≤a.
[题组训练]
1.(2018·忻州第一中学模拟)已知关于x 的不等式x —4x≥m
对任意x ∈[0,1]恒成立,则实数m 的取值范围为 ( )
A. ( 一 0, — 3) B.[—3, 十 一 ]
C.[—3,0] D. [一4,十一]
解析:x —4x≥m对任意x∈(0,1)恒成立,令f(x)=x -4x,
∵f(x)图象的对称轴为直线 x=2,∴f(x) 在(0,1)上单调递减, ∴当x=1 时 ,f(x)取到最小值,为一3,∴实数m 的取值范围 是[一0, — 3],故选A.
答案: A
2.若不等式 x +mx—1<0对于任意x∈[m,m+1] 都成立,则
实数m 的取值范围是
解析:由题意,得函数f(x)=x +mx—1在[m,m+1] 上的
最大值小于0,又抛物线f(x)=x +mx—1开口向上,
所以只需
答案:
一元二次不等式及其解法
一、课前小练
(一)判一判(对的打“ √ ”,错的打“×”)
(1)若不等式 ax +bx+c<0 的解集为(x ,x ),则必有a>0.( √)
(2)若方程ax +bx+c=0(a≠0) 没有实数根,则不等式ax +bx
十c>0的解集为R. (×)
(3)若二次函数y=ax +bx+c 的图象开口向下,则不等式 ax
十bx+c<0 的解集一定不是空集. ( √)
所以不等式2x —x—3>0的解集 故选B.
答案:B
(二)选一选
1. 不等式2x —x—3>0的解集为
B.
解析:由2x —x—3=(2x—3)(x+1)>0,得
x<—1,
( )
2. 若集合M={xlx +5x—14<0},N={xl1
A.0 B.(1,4)
C.(2,4) D.(1,2)
解析:因为M={xlx +5x—14<0}={xl(x—2)·(x+7)<0}=
{xl—7
判别式△=b —4ac 4>0 △=0
4<0
二次函数y=ax + bx+c(a>0)的图象 X1 0 X2 x y 0 X1=X2 x
一元二次方程ax +bx+c=0(a>0) 的根 有 两 个 相 异 实 根 x , x ( x
根
二、基础知识
1. 三个“二次”之间的关系
判别式 4= 4>0 4=0
4<0
一元二次不等式 ax + >0)的解集 {xlx
R
一元二次不等式 ax >0)的解集 {x|x
(1)将不等式化为右边为零,左边为二
次项系数大于零的不等式 ax +bx
十c>0(a>0)或 ax +bx+c<0(a>0).
(2)求出相应的一元二次方程的根.
在不等式 ax +bx+
c>0(a≠0) 中,如果二
次项系数 a<0, 可 根 据不等式的性质,将 其转化为正数.
开口向上的二次不等式的解法顺口溜:
大于取两边,小于取中间.
(3)利用二次函数的图象与x 轴的交点确定一元二次不等式的
解集.
3.一元二次不等式恒成立问题
(1)不等式ax +bx+c>0(a≠0),x∈R 恒成立→a>0 且4<0;
(2)不等式 ax +bx+c<0(a≠0),x∈R 恒成立 a<0 且4<0;
(3)若a 可以为0,需要分类讨论, 一般优先考虑a=0 的
情形.
考点一一元二次不等式的解法
三、典型例题分析
考法(一)不含参数的一元二次不等式
[典例] 解下列不等式:(1)—3x —2x+8≥0;
(2)0
即(3x—4)(x+2)≤0, 解 得
所以原不等式的解集
(2)原不等式等价
0
,
借助于数轴,如图所示, 原不等式的解集为{xl—2≤x<一1或2
计算对应方程的判别式
求出对应的一元二次方程的根,或根据判别式说明
方程有没有实根
利用“大于取两边,小于取中间”写出不等式的解集
[解题技法]
解一元二次不等式的4个步骤
判 求 写
变 —
考法(二)含参数的一元二次不等式
[典例] 解不等式ax —(a+1)x+1<0(a>0).
[解] 原不等式变为(ax—1)(x—1)<0,
因 为a>0, 所 以
所以当a>1, 时,解
当 a=1 时,解集为o; 当 0
当a>1 时,不等式的解集为
[解题技法]
1. 解含参数的一元二次不等式的步骤
(1)若二次项系数含有参数,则应讨论参数是等于0,小于
0 , 还是大于0,然后将不等式转化为二次项系数为正的形式;
(2)判断方程根的个数,讨论判别式△与0的关系;
(3)确定无根时可直接写出解集;确定方程有两个根时,要
讨论两根的大小关系,从而确定不等式的解集.
以(2x+9)(x—1)≤0, 解 得 所以不等式(x+5)(3—
2x)≥6 的解集 .故选D.
答案: D
[题组训练]
1.不 等 式(x+5)(3—2x)≥6 的解集是
解析:不等式(x+5)(3—2x)≥6 可 化 为 2
( )
2. 已知不等式ax —bx—1≥0 的解集是 则不等式
x —bx—a<0 的解集是 ( )
A.(2,3) B. ( 一 , 2 )U(3, 十 一)
C.
解析:由题意知 ,-3是方程ax —bx—1=0的两根,
所以由根与系数的关系
解 不等式x —bx—a<0 即为x —5x+6<0,
解集为(2,3). 答案:A
3. 求不等式12x —ax>a (a∈R)的解集.
解:原不等式可化为12x —ax—a >0,
即(4x+a)(3x—a)>0,
令(4x+a)(3x—a)=0, 解 得 ●
当a>0 时,不等式的解集
当a=0 时,不等式的解集为(一0,0)U(0, 十一);
当a<0 时,不等式的解集为
考点二绝对值不等式
和分式不等式
考法(一)含绝对值不等式的解法
【典例】解下列不等式:
(1)|2x-1≥3(2)|2x-1≥3x-1
(1)解法1:由|2x-1≥3 得2x-1≥3 或2x-1≤-3
故x≥2 或x≤-1:. 解集为{x|x≥2 或x≤-1}
(1)解法2:由|2x-1≥3 得(2x-1) ≥9
故4x -4x-8≥0:. 解集为{x|x≥2 或x≤-1}
(2)解:由|2x-1≥3x-1| 得(2x-1) ≥3x-1|
故5x -2x≤0:解集为{x|0≤x≤
解题技法:解绝对值不等式的一般步骤是:(1)解对应的
方程;(2)把根从小到大排列;(3)利用“大于取两边,
小于取中间”的原则去取解集.特别地,若两边都有
绝对值,则可两边同时平方求解集.
题组训练
(1)|3x-2<4(2)|2x-1≥3x-1
(2)解集为{x|x≤3
(1)解法1:由
∴{x| 或x<-3}
(1)解法2:由
·
:
考法(二)分式不等式的解法
【典例】解下列不等式:
解题技法:解分式不等式的一般步骤是:先移项
(必须把所有的项都移到同一边),再通分;
题组训练:
1-2<-x的解集为
解集为{x|x<-2 或0
问题
考法(一) 在 R 上的恒成立问题
[典例]若不等式(a—2)x +2(a—2)x—4<0 对一切 x∈R 恒成
立,则实数a 的取值范围是 ( )
A. ( 一 , 2 ) B.[—2,2] C.(—2,2) D.(—,—2)
[解析] 当 a—2=0, 即 a=2 时,不等式为一4<0,对一切x ∈R
恒成立.
当a≠2 时,贝
解得—2
日只
[解题技法] 一元二次不等式恒成立的条件
(1)ax +bx+c>0(a≠0)恒成立的充要条件
(2)ax +bx+c<0(a≠0)恒成立的充要条件
考法(二)在给定区间上的恒成立问题
[典例] 若对任意的x∈[—1,2], 都有
常数),则a 的取值范围是 ( )
A. [ 一 0 , — 3 ] B. ( 一 0 , 0 )
C.[1,十 0 ] D. ( 一 0 , 1 )
[解析] 法一:令 f(x)=x —2x+a, 则由题意,得
法二:当x∈[—1,2]时,不等式x —2x+a≤0恒成立等价于a≤
—x +2x恒成立,则由题意,得a≤(—x +2x)min(x∈[-1,2]).而 —x +2x=—(x—1) +1, 则 当x=—1 时,(—x +2x)min=—3, 所
以 a≤—3, 故 选A. [答案] A
f(一1)=(一1) -2×(一1)+a≤0, f(2)=2 -2×2+a≤0,
解得a≤—3, 故选A.
[解题技法]
一元二次不等式在给定区间上的恒成立问题的求解方法
(1)直接转化为最值问题求解:
f(x)≥0 恒成立→f(x)min≥0;
f(x)≤0恒成立→f(x)max≤0.
(2)先分离变量,再转化为最值问题求解:
f(x)≥a恒成立→f(x)min≥a;
f(x)≤a 恒成立→f(x)max≤a.
[题组训练]
1.(2018·忻州第一中学模拟)已知关于x 的不等式x —4x≥m
对任意x ∈[0,1]恒成立,则实数m 的取值范围为 ( )
A. ( 一 0, — 3) B.[—3, 十 一 ]
C.[—3,0] D. [一4,十一]
解析:x —4x≥m对任意x∈(0,1)恒成立,令f(x)=x -4x,
∵f(x)图象的对称轴为直线 x=2,∴f(x) 在(0,1)上单调递减, ∴当x=1 时 ,f(x)取到最小值,为一3,∴实数m 的取值范围 是[一0, — 3],故选A.
答案: A
2.若不等式 x +mx—1<0对于任意x∈[m,m+1] 都成立,则
实数m 的取值范围是
解析:由题意,得函数f(x)=x +mx—1在[m,m+1] 上的
最大值小于0,又抛物线f(x)=x +mx—1开口向上,
所以只需
答案:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
