5.6匀速圆周运动的数学模型及函数y=Asinωx+φ的图象【新教材】人教A版高中数学必修第一册 课件(共25张PPT)
文档属性
| 名称 | 5.6匀速圆周运动的数学模型及函数y=Asinωx+φ的图象【新教材】人教A版高中数学必修第一册 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
第五章 三角函数
5.6 函数y=Asin(wx+φ)
第 1 课 时 匀 速 圆 周运动的数学模型及函数y=Asin(wx+φ)的图象
[学习目标] 1.了解函数y=Asin(wx+φ)的现实背景,经历匀 速圆周运动的数学建模过程,进一步体会三角函数与现实世界的密 切联系,发展数学建模素养.
2.掌握参数A,w,φ 对函数y=Asin(wx+φ)的图象的影响,理解参 数A,w,φ 在圆周运动中的实际意义,发展数学抽象、逻辑推理与直 观想象的素养.
3.理解从正弦曲线到函数 y=Asin(wx+φ)的图象的变换过程,能 用“五点法”作函数y=Asin(wx+φ)的图象.
预习导学 思维启动一
一 、匀速圆周运动的函数模型
[知识梳理]
形如 y=Asin(wx+φ) 函数模型的建立:
模型准备(匀速圆周运动)→模型假设(三角函数模型)→
模型建立(H=rsin(wt+φ)+h).
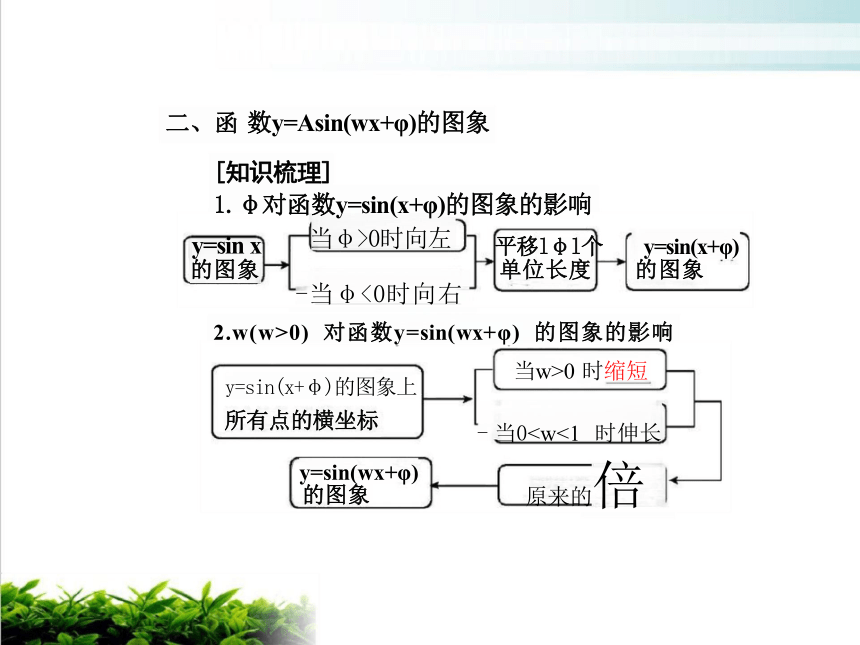
二、函 数y=Asin(wx+φ)的图象
[知识梳理]
1.φ对函数y=sin(x+φ)的图象的影响
y=sin x 当φ>0时向左 平移lφl个 y=sin(x+φ)
的图象 单位长度 的图象
-当φ<0时向右
2.w(w>0) 对函数y=sin(wx+φ) 的图象的影响
当w>0 时缩短
- 当0y=sin(x+φ)的图象上
所有点的横坐标
y=sin(wx+φ) 的图象
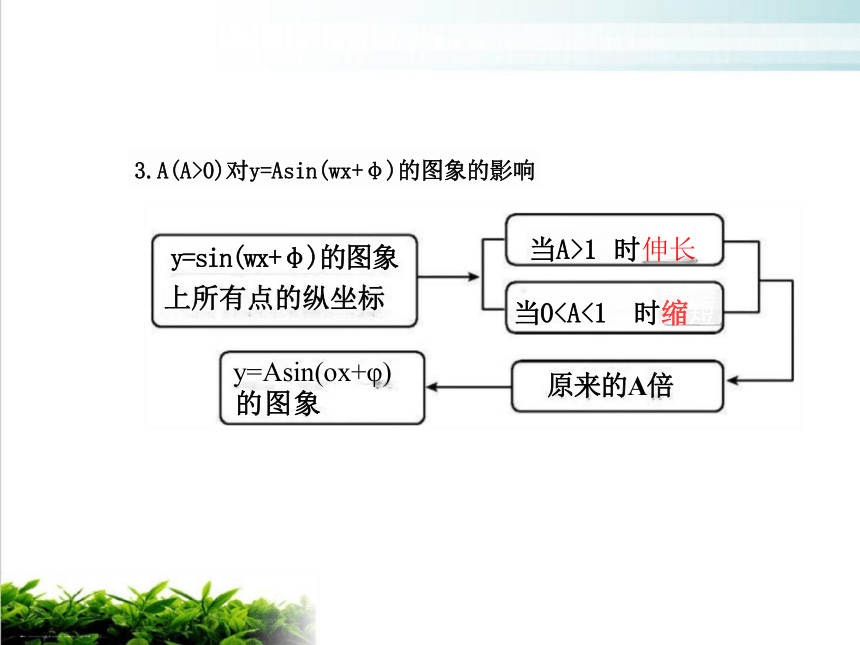
y=sin(wx+φ)的图象
上所有点的纵坐标
y=Asin(ox+φ)
的图象
当A>1 时伸长
当0原来的A倍
3.A(A>0)对y=Asin(wx+φ)的图象的影响
4.函 数y=sin x的图象与y=Asin(wx+φ)(A>0,w>0)的图象关系
正弦曲线 y=sinx 到函数y=Asin(wx+φ)的图象的变换过程:
y=sin x的图象 的图象
所有点的横坐标变为原来的 倍
y=sin(x+φ)的图象 纵坐标不变 y=sin(wx+φ)的图象
所有点的纵坐标变为原来的A倍
y=sin(wx+φ)的图象 横坐标不变 y=Asin(wx+φ)的图象.
【思考】
由函数 y=sin x的图象得到y=Asin(wx+φ)(A>0,w>0)
的图象时必须先进行平移变换吗
[基础测试]
判断.(正确的画“ √ ”,错误的画“×”)
(1)y=sin x 的图象上所有点的横坐标不变,纵坐标变为原来
的2倍所得到的图象对应的函数解析式为
的图象上所有点的横坐标不变,纵坐标变
为原来的 ,所得图象对应的函数解析式为 .( )
重点探究认知发展—
探索点一“五点法”作函数图象及应用
【例1】 已知函数 “五点法”作出
其简图.
解:列表.
2x-3 0 π 3π 2
2π
X 5π 12 2π 3 11π 12
7π
6
y=2sin(2x-3 0 2 0 -2
0
π
6
π
2
描点,连线得函数 在一个周期内的图象.
再将这部分图象向左、向右延伸kπ(k∈Z)个单位长度,
即可得函数 )的图象(如图).
第二步:在同一平面直角坐标系中描出各点.
第三步:用平滑的曲线连接这些点,先得到一个周期
内的图象,再将这部分图象向左、向右延伸整数个周期即 可,得到函数y=Asin(wx+φ)的图象.
wx+φ 0 π 2 π 3 一兀 2
2π
X eia π_ φ 2w w π_ Φ ww 3π φ 20 w
2π φ ww
y 0 A 0 -A
0
方法规律
“五点法”作函数y=Asin(wx+φ)图象的步骤 第一步:列表.
2+3 0 h 1 2 π 3π 2
2π
X 3 π - 3 4π 3 7π 3
10π
3
y 1 - 2 0 1 1 2 0
1
-
2
【跟踪训练】
1.作出函数
解:列表.
在一个周期内的图象.
描点,连线得函数 在一个周期内的图象,如图.
【例2】 (1)要得到
的图象( )
A.向左平移”个单位长度
C. 向左平移 "个单位长度
向左平移
解析:y=3sin 2x的图象—
的图象,即y=3sin(2x+) 的图象.
个单位长度
→y=3sin 2(x+g
B.向右平移
D.向右平移
探索点二三角函数图象之间的变换
个单位长度
个单位长度
)的图象,只需将y=3sin 2x
解析:由题意,y=sin x的图象
的图象个 举vsin2( x+) 的图象即 的
图象.
(2)先把函数y=sin x的图象上所有点的横坐标都缩小到
原来的一半,纵坐标保持不变,再把图象向左平移 个单位长 度,则所得图象对应的函数解析式为( )
B.y=-sin 2x
C.y=cos 2x
(3)若把函数y=f(x)图象上的每一点的纵坐标扩大到原来的
4倍,横坐标扩大到原来的2倍,然后把所得的图象沿x 轴向左平
单位长度,这样得到的图象和y=2sinx 的图象相同,则函数 y=f(x)的解析式为
解析:y=2sin x的图象— 移 的图象
个
的
的图象,即
图象上各点纵坐标缩小为原来的
图 象
的图象.
横坐标不变
天化
方法规律
1.三角函数图象平移变换问题的分类及解题策略
(1)确定函数y=sin x的图象经过平移变换后图象对应 的函数解析式,关键是明确左右平移的方向,按“左加右减” 的原则进行.
(2)已知两个函数解析式判断其图象间的平移关系时, 首先要将函数解析式化为同名三角函数形式,然后再确定 平移方向和长度.
方法规律
2.三角函数图象伸缩变换的方法
方法1:y=A sin w x的图象
y=A sin w x的图象—— →y=A sin w x的图象
方法2:y=A sin w x的图象— —
=Asx 的图象丝标支为原来的 倍y=A sin o x的图象.
倍
来的
标变
横坐标变为原来的 倍
横坐标变为原来的 倍
【跟踪训练】
2.变式练本例题(1)中由
y=3sin 2x的图象,如何平移
解 :由例题知由
的图象应该向右平移"个单位长度
的图象得到y=3sin 2x
)的图象得到
度,再把所得图象上各点的横坐标缩短为原来的 所得图象的 函数解析式为
向右平移4
解析: 的图象 个单位长度y=sin[5(x-2)-2I=
横坐标缩短
的图象 的图象.
3.同类练先将函数
的图象向右平移 个单位长
4.拔高练定义运算: 将函数
的图象向左平移m(m>0) 个单位
长度,所得图象对应的函数g(x)为偶函数,则m 的 最
小值是( )
C.
人
B.
D.
解析:由题意,可知
向左平移m(m>0)个单位长度即为
又因为新函数g(x)为偶函数,由三角函数图象的性质可得, 当x=0 时函数值为最大值或最小值,
即 或
所! 即
又因为m>0, 所以m 的最小值 故选C.
匀速圆周运动
的数学模型
函 数y=Asin(ox+φ) 的图象
φ,W,A 对函数 y=Asin(wx+φ)的 图象的影响
“五点法”作函 数图象的步骤
函数图象的变换 方法
直观想象 数学建模 数学抽象
课堂建构
知识
素养
方法
演讲完毕,谢谢观看!
第五章 三角函数
5.6 函数y=Asin(wx+φ)
第 1 课 时 匀 速 圆 周运动的数学模型及函数y=Asin(wx+φ)的图象
[学习目标] 1.了解函数y=Asin(wx+φ)的现实背景,经历匀 速圆周运动的数学建模过程,进一步体会三角函数与现实世界的密 切联系,发展数学建模素养.
2.掌握参数A,w,φ 对函数y=Asin(wx+φ)的图象的影响,理解参 数A,w,φ 在圆周运动中的实际意义,发展数学抽象、逻辑推理与直 观想象的素养.
3.理解从正弦曲线到函数 y=Asin(wx+φ)的图象的变换过程,能 用“五点法”作函数y=Asin(wx+φ)的图象.
预习导学 思维启动一
一 、匀速圆周运动的函数模型
[知识梳理]
形如 y=Asin(wx+φ) 函数模型的建立:
模型准备(匀速圆周运动)→模型假设(三角函数模型)→
模型建立(H=rsin(wt+φ)+h).
二、函 数y=Asin(wx+φ)的图象
[知识梳理]
1.φ对函数y=sin(x+φ)的图象的影响
y=sin x 当φ>0时向左 平移lφl个 y=sin(x+φ)
的图象 单位长度 的图象
-当φ<0时向右
2.w(w>0) 对函数y=sin(wx+φ) 的图象的影响
当w>0 时缩短
- 当0
所有点的横坐标
y=sin(wx+φ) 的图象
y=sin(wx+φ)的图象
上所有点的纵坐标
y=Asin(ox+φ)
的图象
当A>1 时伸长
当0
3.A(A>0)对y=Asin(wx+φ)的图象的影响
4.函 数y=sin x的图象与y=Asin(wx+φ)(A>0,w>0)的图象关系
正弦曲线 y=sinx 到函数y=Asin(wx+φ)的图象的变换过程:
y=sin x的图象 的图象
所有点的横坐标变为原来的 倍
y=sin(x+φ)的图象 纵坐标不变 y=sin(wx+φ)的图象
所有点的纵坐标变为原来的A倍
y=sin(wx+φ)的图象 横坐标不变 y=Asin(wx+φ)的图象.
【思考】
由函数 y=sin x的图象得到y=Asin(wx+φ)(A>0,w>0)
的图象时必须先进行平移变换吗
[基础测试]
判断.(正确的画“ √ ”,错误的画“×”)
(1)y=sin x 的图象上所有点的横坐标不变,纵坐标变为原来
的2倍所得到的图象对应的函数解析式为
的图象上所有点的横坐标不变,纵坐标变
为原来的 ,所得图象对应的函数解析式为 .( )
重点探究认知发展—
探索点一“五点法”作函数图象及应用
【例1】 已知函数 “五点法”作出
其简图.
解:列表.
2x-3 0 π 3π 2
2π
X 5π 12 2π 3 11π 12
7π
6
y=2sin(2x-3 0 2 0 -2
0
π
6
π
2
描点,连线得函数 在一个周期内的图象.
再将这部分图象向左、向右延伸kπ(k∈Z)个单位长度,
即可得函数 )的图象(如图).
第二步:在同一平面直角坐标系中描出各点.
第三步:用平滑的曲线连接这些点,先得到一个周期
内的图象,再将这部分图象向左、向右延伸整数个周期即 可,得到函数y=Asin(wx+φ)的图象.
wx+φ 0 π 2 π 3 一兀 2
2π
X eia π_ φ 2w w π_ Φ ww 3π φ 20 w
2π φ ww
y 0 A 0 -A
0
方法规律
“五点法”作函数y=Asin(wx+φ)图象的步骤 第一步:列表.
2+3 0 h 1 2 π 3π 2
2π
X 3 π - 3 4π 3 7π 3
10π
3
y 1 - 2 0 1 1 2 0
1
-
2
【跟踪训练】
1.作出函数
解:列表.
在一个周期内的图象.
描点,连线得函数 在一个周期内的图象,如图.
【例2】 (1)要得到
的图象( )
A.向左平移”个单位长度
C. 向左平移 "个单位长度
向左平移
解析:y=3sin 2x的图象—
的图象,即y=3sin(2x+) 的图象.
个单位长度
→y=3sin 2(x+g
B.向右平移
D.向右平移
探索点二三角函数图象之间的变换
个单位长度
个单位长度
)的图象,只需将y=3sin 2x
解析:由题意,y=sin x的图象
的图象个 举vsin2( x+) 的图象即 的
图象.
(2)先把函数y=sin x的图象上所有点的横坐标都缩小到
原来的一半,纵坐标保持不变,再把图象向左平移 个单位长 度,则所得图象对应的函数解析式为( )
B.y=-sin 2x
C.y=cos 2x
(3)若把函数y=f(x)图象上的每一点的纵坐标扩大到原来的
4倍,横坐标扩大到原来的2倍,然后把所得的图象沿x 轴向左平
单位长度,这样得到的图象和y=2sinx 的图象相同,则函数 y=f(x)的解析式为
解析:y=2sin x的图象— 移 的图象
个
的
的图象,即
图象上各点纵坐标缩小为原来的
图 象
的图象.
横坐标不变
天化
方法规律
1.三角函数图象平移变换问题的分类及解题策略
(1)确定函数y=sin x的图象经过平移变换后图象对应 的函数解析式,关键是明确左右平移的方向,按“左加右减” 的原则进行.
(2)已知两个函数解析式判断其图象间的平移关系时, 首先要将函数解析式化为同名三角函数形式,然后再确定 平移方向和长度.
方法规律
2.三角函数图象伸缩变换的方法
方法1:y=A sin w x的图象
y=A sin w x的图象—— →y=A sin w x的图象
方法2:y=A sin w x的图象— —
=Asx 的图象丝标支为原来的 倍y=A sin o x的图象.
倍
来的
标变
横坐标变为原来的 倍
横坐标变为原来的 倍
【跟踪训练】
2.变式练本例题(1)中由
y=3sin 2x的图象,如何平移
解 :由例题知由
的图象应该向右平移"个单位长度
的图象得到y=3sin 2x
)的图象得到
度,再把所得图象上各点的横坐标缩短为原来的 所得图象的 函数解析式为
向右平移4
解析: 的图象 个单位长度y=sin[5(x-2)-2I=
横坐标缩短
的图象 的图象.
3.同类练先将函数
的图象向右平移 个单位长
4.拔高练定义运算: 将函数
的图象向左平移m(m>0) 个单位
长度,所得图象对应的函数g(x)为偶函数,则m 的 最
小值是( )
C.
人
B.
D.
解析:由题意,可知
向左平移m(m>0)个单位长度即为
又因为新函数g(x)为偶函数,由三角函数图象的性质可得, 当x=0 时函数值为最大值或最小值,
即 或
所! 即
又因为m>0, 所以m 的最小值 故选C.
匀速圆周运动
的数学模型
函 数y=Asin(ox+φ) 的图象
φ,W,A 对函数 y=Asin(wx+φ)的 图象的影响
“五点法”作函 数图象的步骤
函数图象的变换 方法
直观想象 数学建模 数学抽象
课堂建构
知识
素养
方法
演讲完毕,谢谢观看!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
