第一章章末梳理1-【新教材】人教A版(2019)高中数学必修第一册课件(共44张PPT)
文档属性
| 名称 | 第一章章末梳理1-【新教材】人教A版(2019)高中数学必修第一册课件(共44张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 686.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 00:00:00 | ||
图片预览










文档简介
(共44张PPT)
第一章
集合与常用逻辑用语
章末梳理
目录 CONTENTS
知识结构·理脉络
要点梳理·晰精华
素养突破·提技能
高考链接·悟考情
·第一册·RJA)
知识结构·理脉络
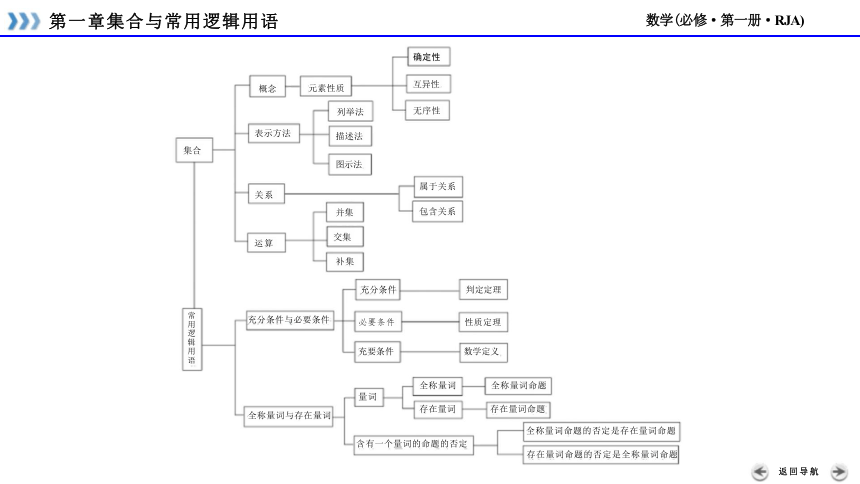
》》》第一章集合与常用逻辑用语
返回导航
数学(必修
交集
补集
充分条件 判定定理
必要条件 性质定理
充要条件 数学定义
全称量词 全称量词命题
量词
存在量词 存在量词命题
全称量词命题的否定是存在量词命题
运算
充分条件与必要条件
全称量词与存在量词
含有一个量词的命题的否定
存在量词命题的否定是全称量词命题
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
元素性质
列举法
确定性
互异性
无序性
属于关系
包含关系
描述法
图示法
常用逻辑用语
表示方法
关系
概念
集合
并集
·第一册·RJA)
要点梳理·晰精华
》》》第一章集合与常用逻辑用语
返回导航
数学(必修
要点梳理·晰精华
本章我们学习了集合的有关概念、关系和运算,还学习了充分条
件、必要条件、充要条件,全称量词、存在量词、全称量词命题与存在 量词命题及它们的否定.这些知识在后续学习中会得到大量应用,是进 一步学习的重要基础.
为了有效使用集合语言表述数学的研究对象,首先应掌握集合语言
的表述方式.为此,我们先学习了集合的含义,明确了集合中元素的确 定性、无序性和互异性等特征;
集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
第一章
再学习了列举法、描述法等集合的表示法,其中描述法利用了研究对象
的某种特征,需要先理解研究对象的性质;类比数与数的关系,我们研 究了集合之间的包含关系与相等关系,这些关系是由元素与集合的关系 决定的,其中集合的相等关系很重要;类比数的运算,我们学习了集合 的交、并、补运算,通过这些运算可以得到与原有集合紧密关联的集 合,由此可以表示研究对象的某些关系,从中我们可以体会到,数学中 的运算并不局限于数的运算,这对提升我们的数学运算素养是很有意义 的.在学习中,要注意“集合的含义与表示一集合的关系-集合的运算” 这个研究路径.
返回导航
集合与常用逻辑用语
数学(必修·第一册·RJA)
第一章
常用逻辑用语是数学语言的重要组成部分,是逻辑思维的基本语
言,也是数学表达和交流的工具.结合初中学过的平面几何和代数知 识,我们学习了常用逻辑用语,发现初中学过的数学定义、定理、命题 都可以用常用逻辑用语表达,利用常用逻辑用语表述数学内容、进行推 理论证,可以大大提升表述的逻辑性和准确性,从而提升我们的逻辑推 理素养.
本章的学习不仅要为后续学习做好知识技能的准备,更重要的是要
为整个高中数学学习做好心理准备,初步形成适合高中数学学习的方式 方法,使我们能更好地适应高中数学学习.
返回导航
集合与常用逻辑用语
数学(必修·第一册·RJA)
第一章
1. 集合中的元素具有确定性、互异性和无序性,你能结合例子说明
这些特性吗
例如,确定性:2∈Q, C
互异性:给定集合{x,x }, 则x≠x , 即 x≠0,1;
无序性:{1,2,3}={3,2,1}.
2. 你能用集合表示平面内线段AB 的垂直平分线吗 结合集合的描
述法谈谈你的体会.
平面内线段AB 的垂直平分线可以表示为{P|PA|=|PB|}.
返回导航
集合与常用逻辑用语
数学(必修·第一册·RJA)
第一章
3. 用联系的观点看问题,可以使我们更深刻地理解数学知识.本章
中,我们类比数与数的关系和运算研究了集合与集合的关系和运算.你 认为这样的类比对发现和提出集合的问题有什么意义 你能类比数的减 法运算给出集合的减法运算吗
集合的减法运算: CyA={x|x∈U, 且x∈A}, 或 A—B={x|x∈A 且
x ∈B}.
4.对给定的p 和q, 如何判定p是q的充分不必要条件、必要不充分条
件、充要条件、既不充分也不必要条件 你能举例说明吗
集合与常用逻辑用语
数学(必修·第一册·RJA)
第一章
返回导航
方法 解读
适合题型
定义 法 第一步,分清条件和结论:分清谁是条 件,谁是结论;第二步,找推式:判断 “p=q”及“q=p”的真假;第三步, 下结论:根据推式及定义下结论
定义法是判断充分、必 要条件最根本、最适用 的方法
集合 法 记条件p, q对应的集合分别是A, B . 若A B,则p是q的充分不必要条 件;若A B,则p是q的必要不充分条 件;若A=B,则p是q的充要条件
适用于“当所要判断的
命题与方程的根、不等
式的解集以及集合有
关,或所描述的对象可
以用集合表示”的情况
熟记判断充分、必要条件的2种方法
集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导
第一章
5.如何否定含有一个量词的全称量词命题和存在量词命题 你能举例
说明吗
否定含有一个量词的命题分两步:
(1)改写量词:找到命题所含的量词,没有量词的要结合命题的含义
加上量词,再改变量词.
(2)否定结论:对原命题的结论进行否定.
数学(必修·第一册·RJA)
集合与常用逻辑用语
返回导航
第一章
·第一册·RJA)
素养突破·提技能
》》》第一章集合与常用逻辑用语
返回导航
数学(必修
考查方向 集合的基本概念
例 1 (1)集合M={x|ax —3x—2=0,a∈R}
数a的值是 0 或
(2)已知集合A={m+2,2m +m}, 若3∈A,
中只有一个元素,则实
则m的值为
数学抽象
核心素养一
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
—2=0只有一个根.
当 a=0 时,方程为一3x—2=0, 只有一个根
=(一3) -4×a× (一2)=0,得
综上所述,a的值是0或
[解析] (1)由题意可知若集合M 中只有一个元素,则方程 ax -3x
》》》第一章集合与常用逻辑用语
当 a≠0 时,△
数学(必修·第一册·RJA)
返回导航
(2)因为3∈A, 则 m+2=3 或 2m +m=3.
当m+2=3, 即 m=1 时 ,m+2=2m +m, 不符合题意,故舍去;
当 2m +m=3, 即 m=1 或 ,m=1 不合题意,若
+2≠2m +m, 满足题意,故
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
[归纳提升]解决集合的概念问题的关注点
(1)研究一个集合,首先要看集合中的代表元素,然后再看元素的限
制条件.当集合用描述法表示时,注意弄清元素表示的意义是什么.
(2)对于含有字母的集合,在求出字母的值后,要注意检验集合的元
素是否满足互异性.
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
考查方向 集合基本运算
例 2(1)设全集U={x∈N*|x<6},集合A={1,3},B={3,5}, 则
UB) 等于( D )
A.{1,4} B.{1,5}
C.{2,5} D.{2,4}
数学运算
核心素养二
》》》第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
(2)设集合A={-1,2,7},B={x|x —7x+m=0}, 若A∩B={2}, 则B
=(C)
A.{2,—10} B.{2,0}
C.{2,5} D.{2,10}
[解析] (1)因为U={1,2,3,4,5},AUB={1,3,5}, 所以Cu(AUB)=
{2,4}.
(2)由题意知2是方程x -7x+m=0 的解,把x=2 代入方程得m=10,
因为x -7x+10=0 的解为x=2 或x=5, 所以B={2,5}.故选C.
》》》第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
[归纳提升]集合基本运算的方法
一般来讲,集合中的元素若是离散的,则用Venn图表示;集合中的
元素若是连续的实数,则用数轴表示,此时要注意端点的情况.
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
考查方向 利用集合运算求参数
例 3 (1)已知集合A={1,3,m},B={1,m},AUB=A, 则 m
等于( B )
A.0 或 3 B.0 或 3
C.1 或 √3 D.1 或 3
(2)设集合A={0,1}, 集 合B={x|x>a}, 若A∩B=0, 则实数a 的取
值范围是( B )
A.{a|a≤1} B.{a|a≥1}
C.{a|a≥0} D.{a|a≤0}
返回导航
集合与常用逻辑用语
数学(必修·第一册·RJA)
第一章
[解析] (1)由AUB=A 知BEA, 所 以 或 m=√m. 当m=3时,A={1,3,√3},B={1,3}, 满足AUB=A;
若m=√m, 即m=1 或0,当m=1时, √m=1,不合题意,舍去, 当m=0时,A={1,3,0},B={1,0},满足AUB=A.
(2)因为A∩B=0, 所以0∈B, 且 1 4B, 所 以a≥1.
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
[归纳提升]利用集合的运算求参数的范围的注意点
(1)要弄清楚集合运算的结果或可能的结果,再根据其中的结果判定
参数的值或范围.
(2)当集合的运算较为复杂时,要借助于数轴或韦恩图解决问题.
(3)注意参数的值或范围应该满足集合中元素的互异性.
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
考查方向 集合运算的综合应用
例 4 已知集合A={x|0≤x≤2},B={x|a≤x≤a
+3}.
(1)若(CgA)UB=R, 求a 的取值范围;
(2)是否存在a,使 (CgA)UB=R 且ANB=0
[解析](1)因为A={x|0≤x<2},
所以CgA={x|x<0或x>2}
因为(CgA)UB=R.(如图)
直观想象
核心素养
集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
第一章
所以
所以- 1≤a≤0. 即a 的取值范围是[一1,0].
(2)由(1)知当(lrA)U B=R 时, —1≤a≤0, 则 a+3∈[2,3],
所以ASB, 这与A∩B=0 矛盾.
即这样的a 不存在.
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
[归纳提升]集合运算的综合应用的注意点
(1)进行集合的运算时要看集合的组成,并且要对有的集合进行化
简 .
(2)涉及含字母的集合时,要注意该集合是否可能为空集.
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
考查方向 充分必要条件的判断
例 5 设 集 合S={0,a},T={x∈Z|x <2}, 则 “a=1” 是
“Sc 充”分的必要 条件 . (填“充分不必要”“必要不充
分”“充要”或“既不充分也不必要”)
[解析] T={x∈Z|x <2}={-1,0,1},a=1 时 ,S={0,1}, 所以SET;
反之,若SCT, 则 S={0,1}或S={0,-1}. 所 以“a=1” 是 “SCT”
的充分不必要条件.
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
[归纳提升]充分(必要)条件是学习中的一个难点.要解决这个难
点,将抽象的概念用直观、形象的图形表示出来,看得见、想得通,才 是最好的方法.本章使用集合模型对充要条件的外延与内涵作了直观形 象的解释,实践证明效果较好.集合模型解释如下:(1)A是B 的充分条
第一章集合与常用逻辑用语
件,即AEB.
数学(必修·第一册·RJA)
返回导航
(2)A是 B 的必要条件,即BEA.
(3)A是 B 的充要条件,即A=B.
集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
第一章
(4)A是B的即不充分也不必要条件,
即ANB=0 或A,B 既有公共元素也有非公共元素
A B 或 A B
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
考查方向 充分必要条件的判断
例 6 设集合M={x|x>2},P={x|x<3}, 那 么“x∈M或x ∈P” 是
“x∈(PNM)”的 必要不充分 条件.(填“充分不必要”“必要不充 分”“充要”或“既不充分也不必要”)
逻辑推理
核心素养四
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
[解析] 条件p:x∈M 或x∈P; 结论q:x∈(PNM).
若x∈M, 则 x 不一定属于P, 即 x 不一定属于PNM, 所 以p≠q;
若x∈(P∩M),则x∈M 且x∈P,所以q→p.综上知, “x∈M 或x∈P”
是“x∈(P∩M)”的必要不充分条件.
[归纳提升]利用定义判断充分必要条件的方法
如果p=q, 那么称p 是q的充分条件,同时称q是p的必要条件.判断
时的关键是分清条件与结论.
集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
第一章
考查方向 利用充分必要条件求参数的取值范围
例7 已知p:—2≤x≤10,q:1—m≤x≤1十
m(m>0), 若p是g的充分不必要条件,则m的取值范围是
集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
第一章
[解析] 设p,q 分别对应集合P,Q,
则P={x|-2≤x≤10},Q={x|1—m≤x≤1+m(m>0)},
由题意知p→q, 但q≠p, 故P Q,
解得m≥9, 即 m 的取值范围是{mlm≥9}.
》》》第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
所以
或
[归纳提升] 运用集合思想来判断充分条件和必要条件是一种行之
有效的方法,若p 以非空集合A 的形式出现,q 以非空集合B 的形式出 现,则①若AEB, 则 p 是 q 的充分条件;②若BSA, 则 p 是 q 的必要 条件;③若A B,则p 是 q 的充分不必要条件;④若B A,则p 是 q 的 必要不充分条件;⑤若A=B, 则 p 是 q 的充要条件.
集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
第一章
·第一册·RJA)
高考链接·悟考情
》》》第一章集合与常用逻辑用语
返回导航
数学(必修
A.{x|x>-1} B.{x|x<2}
C.{x|-1[解析] ∵A={x|x>-1},B={x|x<2},
∴ANB={x|-11.(2019·全国Ⅱ高考)已知集合A={x|x>-1},B={x|x<2}, 则A∩B
=(C)
》》》第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
2. 已知集合A={(x,y)|x +y ≤3,x∈Z,y∈Z}, 则A中元素的个数
为( A )
A.9 B.8
C.5 D.4
[解析] 将满足x +y ≤3的整数数对(x,y) 全部列举出来,即(-1,-
1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1),共 有9个,故选A.
》》》第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
3. 设集合A={—1,2,6},B={x|x —5x+m=0}, 若3∈(AUB), 则B
=(C)
A.{3,—6} B.{3,—2}
C.{3,2} D.{3,6}
[解析] 因为3∈(AUB), 所以3∈B, 于是32-5×3+ m=0, m
=6.故B={x|x -5x+6=0}={2,3}. 故选C.
》》第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
4.命题“Vx∈R, 3n∈N+, 使得n≥x ”的否定形式是( D
A.Vx∈ R, 3n∈N+, 使得nB.Vx∈ R, Vn∈N+, 使得nC.3x∈ R, 3n∈N+, 使得nD.3x∈ R, Vn∈N+, 使得n[解析] 将“V”改写为“3”,“3”改写为“V”, 再否定结论可
得,命题的否定为“3x∈R,Vn∈N+, 使得n第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
5.(2019·上海高考)已知集合A={1,2,3,4,5},B={3,5,6}, 则A∩B=
{3,5}
[解析] ∵集合A={1,2,3,4,5},B={3,5,6},∴A∩B={3,5}.
6.某网店统计了连续三天售出商品的种类情况:第一天售出19种商
品,第二天售出13种商品,第三天售出18种商品;前两天都售出的商品 有3种,后两天都售出的商品有4种.则该网店
(1)第一天售出但第二天未售出的商品有 16 种;
(2)这三天售出的商品最少有 29 种 .
集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
第一章
(2)由(1)知,前两天售出的商品为19+13-3=29(种),当第三天售出
的18种都是前两天售出的商品时,这三天售出的商品种类最少,售出的 商品最少为29种.
返回导航
[解析] (1)设第一天售出的商品为集合A, 则A 中有19个元素,第二
天售出的商品为集合B, 则B中有13个元素.由于前两天都售出的商品有3 种,则A∩B中有3个元素,如图所示,所以该网店第一天售出但第二天未
售出的商品有19-3=16(种).
集合与常用逻辑用语
数学(必修·第一册·RJA)
第一章
演示完毕
谢谢欣赏
第一章
集合与常用逻辑用语
章末梳理
目录 CONTENTS
知识结构·理脉络
要点梳理·晰精华
素养突破·提技能
高考链接·悟考情
·第一册·RJA)
知识结构·理脉络
》》》第一章集合与常用逻辑用语
返回导航
数学(必修
交集
补集
充分条件 判定定理
必要条件 性质定理
充要条件 数学定义
全称量词 全称量词命题
量词
存在量词 存在量词命题
全称量词命题的否定是存在量词命题
运算
充分条件与必要条件
全称量词与存在量词
含有一个量词的命题的否定
存在量词命题的否定是全称量词命题
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
元素性质
列举法
确定性
互异性
无序性
属于关系
包含关系
描述法
图示法
常用逻辑用语
表示方法
关系
概念
集合
并集
·第一册·RJA)
要点梳理·晰精华
》》》第一章集合与常用逻辑用语
返回导航
数学(必修
要点梳理·晰精华
本章我们学习了集合的有关概念、关系和运算,还学习了充分条
件、必要条件、充要条件,全称量词、存在量词、全称量词命题与存在 量词命题及它们的否定.这些知识在后续学习中会得到大量应用,是进 一步学习的重要基础.
为了有效使用集合语言表述数学的研究对象,首先应掌握集合语言
的表述方式.为此,我们先学习了集合的含义,明确了集合中元素的确 定性、无序性和互异性等特征;
集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
第一章
再学习了列举法、描述法等集合的表示法,其中描述法利用了研究对象
的某种特征,需要先理解研究对象的性质;类比数与数的关系,我们研 究了集合之间的包含关系与相等关系,这些关系是由元素与集合的关系 决定的,其中集合的相等关系很重要;类比数的运算,我们学习了集合 的交、并、补运算,通过这些运算可以得到与原有集合紧密关联的集 合,由此可以表示研究对象的某些关系,从中我们可以体会到,数学中 的运算并不局限于数的运算,这对提升我们的数学运算素养是很有意义 的.在学习中,要注意“集合的含义与表示一集合的关系-集合的运算” 这个研究路径.
返回导航
集合与常用逻辑用语
数学(必修·第一册·RJA)
第一章
常用逻辑用语是数学语言的重要组成部分,是逻辑思维的基本语
言,也是数学表达和交流的工具.结合初中学过的平面几何和代数知 识,我们学习了常用逻辑用语,发现初中学过的数学定义、定理、命题 都可以用常用逻辑用语表达,利用常用逻辑用语表述数学内容、进行推 理论证,可以大大提升表述的逻辑性和准确性,从而提升我们的逻辑推 理素养.
本章的学习不仅要为后续学习做好知识技能的准备,更重要的是要
为整个高中数学学习做好心理准备,初步形成适合高中数学学习的方式 方法,使我们能更好地适应高中数学学习.
返回导航
集合与常用逻辑用语
数学(必修·第一册·RJA)
第一章
1. 集合中的元素具有确定性、互异性和无序性,你能结合例子说明
这些特性吗
例如,确定性:2∈Q, C
互异性:给定集合{x,x }, 则x≠x , 即 x≠0,1;
无序性:{1,2,3}={3,2,1}.
2. 你能用集合表示平面内线段AB 的垂直平分线吗 结合集合的描
述法谈谈你的体会.
平面内线段AB 的垂直平分线可以表示为{P|PA|=|PB|}.
返回导航
集合与常用逻辑用语
数学(必修·第一册·RJA)
第一章
3. 用联系的观点看问题,可以使我们更深刻地理解数学知识.本章
中,我们类比数与数的关系和运算研究了集合与集合的关系和运算.你 认为这样的类比对发现和提出集合的问题有什么意义 你能类比数的减 法运算给出集合的减法运算吗
集合的减法运算: CyA={x|x∈U, 且x∈A}, 或 A—B={x|x∈A 且
x ∈B}.
4.对给定的p 和q, 如何判定p是q的充分不必要条件、必要不充分条
件、充要条件、既不充分也不必要条件 你能举例说明吗
集合与常用逻辑用语
数学(必修·第一册·RJA)
第一章
返回导航
方法 解读
适合题型
定义 法 第一步,分清条件和结论:分清谁是条 件,谁是结论;第二步,找推式:判断 “p=q”及“q=p”的真假;第三步, 下结论:根据推式及定义下结论
定义法是判断充分、必 要条件最根本、最适用 的方法
集合 法 记条件p, q对应的集合分别是A, B . 若A B,则p是q的充分不必要条 件;若A B,则p是q的必要不充分条 件;若A=B,则p是q的充要条件
适用于“当所要判断的
命题与方程的根、不等
式的解集以及集合有
关,或所描述的对象可
以用集合表示”的情况
熟记判断充分、必要条件的2种方法
集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导
第一章
5.如何否定含有一个量词的全称量词命题和存在量词命题 你能举例
说明吗
否定含有一个量词的命题分两步:
(1)改写量词:找到命题所含的量词,没有量词的要结合命题的含义
加上量词,再改变量词.
(2)否定结论:对原命题的结论进行否定.
数学(必修·第一册·RJA)
集合与常用逻辑用语
返回导航
第一章
·第一册·RJA)
素养突破·提技能
》》》第一章集合与常用逻辑用语
返回导航
数学(必修
考查方向 集合的基本概念
例 1 (1)集合M={x|ax —3x—2=0,a∈R}
数a的值是 0 或
(2)已知集合A={m+2,2m +m}, 若3∈A,
中只有一个元素,则实
则m的值为
数学抽象
核心素养一
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
—2=0只有一个根.
当 a=0 时,方程为一3x—2=0, 只有一个根
=(一3) -4×a× (一2)=0,得
综上所述,a的值是0或
[解析] (1)由题意可知若集合M 中只有一个元素,则方程 ax -3x
》》》第一章集合与常用逻辑用语
当 a≠0 时,△
数学(必修·第一册·RJA)
返回导航
(2)因为3∈A, 则 m+2=3 或 2m +m=3.
当m+2=3, 即 m=1 时 ,m+2=2m +m, 不符合题意,故舍去;
当 2m +m=3, 即 m=1 或 ,m=1 不合题意,若
+2≠2m +m, 满足题意,故
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
[归纳提升]解决集合的概念问题的关注点
(1)研究一个集合,首先要看集合中的代表元素,然后再看元素的限
制条件.当集合用描述法表示时,注意弄清元素表示的意义是什么.
(2)对于含有字母的集合,在求出字母的值后,要注意检验集合的元
素是否满足互异性.
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
考查方向 集合基本运算
例 2(1)设全集U={x∈N*|x<6},集合A={1,3},B={3,5}, 则
UB) 等于( D )
A.{1,4} B.{1,5}
C.{2,5} D.{2,4}
数学运算
核心素养二
》》》第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
(2)设集合A={-1,2,7},B={x|x —7x+m=0}, 若A∩B={2}, 则B
=(C)
A.{2,—10} B.{2,0}
C.{2,5} D.{2,10}
[解析] (1)因为U={1,2,3,4,5},AUB={1,3,5}, 所以Cu(AUB)=
{2,4}.
(2)由题意知2是方程x -7x+m=0 的解,把x=2 代入方程得m=10,
因为x -7x+10=0 的解为x=2 或x=5, 所以B={2,5}.故选C.
》》》第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
[归纳提升]集合基本运算的方法
一般来讲,集合中的元素若是离散的,则用Venn图表示;集合中的
元素若是连续的实数,则用数轴表示,此时要注意端点的情况.
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
考查方向 利用集合运算求参数
例 3 (1)已知集合A={1,3,m},B={1,m},AUB=A, 则 m
等于( B )
A.0 或 3 B.0 或 3
C.1 或 √3 D.1 或 3
(2)设集合A={0,1}, 集 合B={x|x>a}, 若A∩B=0, 则实数a 的取
值范围是( B )
A.{a|a≤1} B.{a|a≥1}
C.{a|a≥0} D.{a|a≤0}
返回导航
集合与常用逻辑用语
数学(必修·第一册·RJA)
第一章
[解析] (1)由AUB=A 知BEA, 所 以 或 m=√m. 当m=3时,A={1,3,√3},B={1,3}, 满足AUB=A;
若m=√m, 即m=1 或0,当m=1时, √m=1,不合题意,舍去, 当m=0时,A={1,3,0},B={1,0},满足AUB=A.
(2)因为A∩B=0, 所以0∈B, 且 1 4B, 所 以a≥1.
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
[归纳提升]利用集合的运算求参数的范围的注意点
(1)要弄清楚集合运算的结果或可能的结果,再根据其中的结果判定
参数的值或范围.
(2)当集合的运算较为复杂时,要借助于数轴或韦恩图解决问题.
(3)注意参数的值或范围应该满足集合中元素的互异性.
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
考查方向 集合运算的综合应用
例 4 已知集合A={x|0≤x≤2},B={x|a≤x≤a
+3}.
(1)若(CgA)UB=R, 求a 的取值范围;
(2)是否存在a,使 (CgA)UB=R 且ANB=0
[解析](1)因为A={x|0≤x<2},
所以CgA={x|x<0或x>2}
因为(CgA)UB=R.(如图)
直观想象
核心素养
集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
第一章
所以
所以- 1≤a≤0. 即a 的取值范围是[一1,0].
(2)由(1)知当(lrA)U B=R 时, —1≤a≤0, 则 a+3∈[2,3],
所以ASB, 这与A∩B=0 矛盾.
即这样的a 不存在.
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
[归纳提升]集合运算的综合应用的注意点
(1)进行集合的运算时要看集合的组成,并且要对有的集合进行化
简 .
(2)涉及含字母的集合时,要注意该集合是否可能为空集.
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
考查方向 充分必要条件的判断
例 5 设 集 合S={0,a},T={x∈Z|x <2}, 则 “a=1” 是
“Sc 充”分的必要 条件 . (填“充分不必要”“必要不充
分”“充要”或“既不充分也不必要”)
[解析] T={x∈Z|x <2}={-1,0,1},a=1 时 ,S={0,1}, 所以SET;
反之,若SCT, 则 S={0,1}或S={0,-1}. 所 以“a=1” 是 “SCT”
的充分不必要条件.
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
[归纳提升]充分(必要)条件是学习中的一个难点.要解决这个难
点,将抽象的概念用直观、形象的图形表示出来,看得见、想得通,才 是最好的方法.本章使用集合模型对充要条件的外延与内涵作了直观形 象的解释,实践证明效果较好.集合模型解释如下:(1)A是B 的充分条
第一章集合与常用逻辑用语
件,即AEB.
数学(必修·第一册·RJA)
返回导航
(2)A是 B 的必要条件,即BEA.
(3)A是 B 的充要条件,即A=B.
集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
第一章
(4)A是B的即不充分也不必要条件,
即ANB=0 或A,B 既有公共元素也有非公共元素
A B 或 A B
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
考查方向 充分必要条件的判断
例 6 设集合M={x|x>2},P={x|x<3}, 那 么“x∈M或x ∈P” 是
“x∈(PNM)”的 必要不充分 条件.(填“充分不必要”“必要不充 分”“充要”或“既不充分也不必要”)
逻辑推理
核心素养四
第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
[解析] 条件p:x∈M 或x∈P; 结论q:x∈(PNM).
若x∈M, 则 x 不一定属于P, 即 x 不一定属于PNM, 所 以p≠q;
若x∈(P∩M),则x∈M 且x∈P,所以q→p.综上知, “x∈M 或x∈P”
是“x∈(P∩M)”的必要不充分条件.
[归纳提升]利用定义判断充分必要条件的方法
如果p=q, 那么称p 是q的充分条件,同时称q是p的必要条件.判断
时的关键是分清条件与结论.
集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
第一章
考查方向 利用充分必要条件求参数的取值范围
例7 已知p:—2≤x≤10,q:1—m≤x≤1十
m(m>0), 若p是g的充分不必要条件,则m的取值范围是
集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
第一章
[解析] 设p,q 分别对应集合P,Q,
则P={x|-2≤x≤10},Q={x|1—m≤x≤1+m(m>0)},
由题意知p→q, 但q≠p, 故P Q,
解得m≥9, 即 m 的取值范围是{mlm≥9}.
》》》第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
所以
或
[归纳提升] 运用集合思想来判断充分条件和必要条件是一种行之
有效的方法,若p 以非空集合A 的形式出现,q 以非空集合B 的形式出 现,则①若AEB, 则 p 是 q 的充分条件;②若BSA, 则 p 是 q 的必要 条件;③若A B,则p 是 q 的充分不必要条件;④若B A,则p 是 q 的 必要不充分条件;⑤若A=B, 则 p 是 q 的充要条件.
集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
第一章
·第一册·RJA)
高考链接·悟考情
》》》第一章集合与常用逻辑用语
返回导航
数学(必修
A.{x|x>-1} B.{x|x<2}
C.{x|-1
∴ANB={x|-1
=(C)
》》》第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
2. 已知集合A={(x,y)|x +y ≤3,x∈Z,y∈Z}, 则A中元素的个数
为( A )
A.9 B.8
C.5 D.4
[解析] 将满足x +y ≤3的整数数对(x,y) 全部列举出来,即(-1,-
1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1),共 有9个,故选A.
》》》第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
3. 设集合A={—1,2,6},B={x|x —5x+m=0}, 若3∈(AUB), 则B
=(C)
A.{3,—6} B.{3,—2}
C.{3,2} D.{3,6}
[解析] 因为3∈(AUB), 所以3∈B, 于是32-5×3+ m=0, m
=6.故B={x|x -5x+6=0}={2,3}. 故选C.
》》第一章集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
4.命题“Vx∈R, 3n∈N+, 使得n≥x ”的否定形式是( D
A.Vx∈ R, 3n∈N+, 使得n
得,命题的否定为“3x∈R,Vn∈N+, 使得n
数学(必修·第一册·RJA)
返回导航
5.(2019·上海高考)已知集合A={1,2,3,4,5},B={3,5,6}, 则A∩B=
{3,5}
[解析] ∵集合A={1,2,3,4,5},B={3,5,6},∴A∩B={3,5}.
6.某网店统计了连续三天售出商品的种类情况:第一天售出19种商
品,第二天售出13种商品,第三天售出18种商品;前两天都售出的商品 有3种,后两天都售出的商品有4种.则该网店
(1)第一天售出但第二天未售出的商品有 16 种;
(2)这三天售出的商品最少有 29 种 .
集合与常用逻辑用语
数学(必修·第一册·RJA)
返回导航
第一章
(2)由(1)知,前两天售出的商品为19+13-3=29(种),当第三天售出
的18种都是前两天售出的商品时,这三天售出的商品种类最少,售出的 商品最少为29种.
返回导航
[解析] (1)设第一天售出的商品为集合A, 则A 中有19个元素,第二
天售出的商品为集合B, 则B中有13个元素.由于前两天都售出的商品有3 种,则A∩B中有3个元素,如图所示,所以该网店第一天售出但第二天未
售出的商品有19-3=16(种).
集合与常用逻辑用语
数学(必修·第一册·RJA)
第一章
演示完毕
谢谢欣赏
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
