人教版2024年八年级上册数学知识点分类训练 :11.1 与三角形有关的线段 (含答案)
文档属性
| 名称 | 人教版2024年八年级上册数学知识点分类训练 :11.1 与三角形有关的线段 (含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 349.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-01 10:34:01 | ||
图片预览



文档简介
人教版2024年八年级上册知识分类训练
11.1 与三角形有关的线段
一.三角形的分类
1、定义:由不在同一直线上的三条线段首尾顺次相接组成的图形叫做三角形。
2、三角形相关定义:三角形有三条边,三个内角,三个顶点.组成三角形的线段叫做三角形的边;相邻两边所组成的角叫做三角形的内角;相邻两边的公共端点是三角形的顶点。
3、符号表示:三角形ABC用符号表示为△ABC,三角形ABC的边AB可用边AB所对的角C的小写字母c表示,AC可用b表示,BC可用a表示.三个顶点用大写字母A,B,C来表示。
4、三角形根据不同的分类依据可分为不同类型:
①、按角分:1、锐角三角形;2、直角三角形;3、钝角三角形。
②、按边分:1、不等边三角形;2、等腰三角形;3、等边三角形(特殊等腰三角形)。
针对训练
1.图中的三角形被木板遮住了一部分,这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.以上都有可能
2.下列分类正确的是( )
A.三角形可分为等腰三角形、等边三角形
B.三角形可分为不等边三角形、等腰三角形以及等边三角形
C.三角形可分为不等边三角形和等边三角形
D.三角形可分为不等边三角形和等腰三角形
3.△ABC的三角之比是1:2:3,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.无法确定
4.如图,以BE为边的三角形有 个.
5.在一节数学活动课上,小敏同学用火柴棍拼成一排由三角形组成的图形,如图所示.按照这种方式继续拼下去,若图形中用了41根火柴棍,则图形中含有 个三角形.
6.图中有几个三角形?用符号表示这些三角形.
二.三角形的三边关系
1、三角形的三边关系:三角形的任意两边之和大于第三边;任意两边之差小于第三边.
注意:(1)三边关系的依据是:两点之间线段是短;
(2)围成三角形的条件是任意两边之和大于第三边.
针对训练
7.下列各组中的三条线段,能组成三角形的是( )
A.1,2,3 B.1,2,4 C.2,2,4 D.4,5,6
8.如图,人字梯的支架AB,AC的长度都为2米,则B,C两点之间的距离可能是( )
A.3米 B.4.2米 C.5米 D.6米
9.若三角形的两边长分别为5和7,则其第三边c的取值范围是( )
A.5<c<7 B.3≤c≤11 C.2<c<12 D.2≤c≤12
10.若一个三角形的边长均为整数,且两边长分别为3和5,则这样的三角形共有 个.
11.三边长不等的△ABC的两条边长分别为2和3,则且第三边长为整数值,则这个三角形的第三边长为 .
12.已知:a、b、c为△ABC的三边长,且a、b满足|2a﹣b+2|+(a+b﹣8)2=0.
(1)求c的取值范围;
(2)在(1)的条件下,若2x﹣c=1,求x的取值范围.
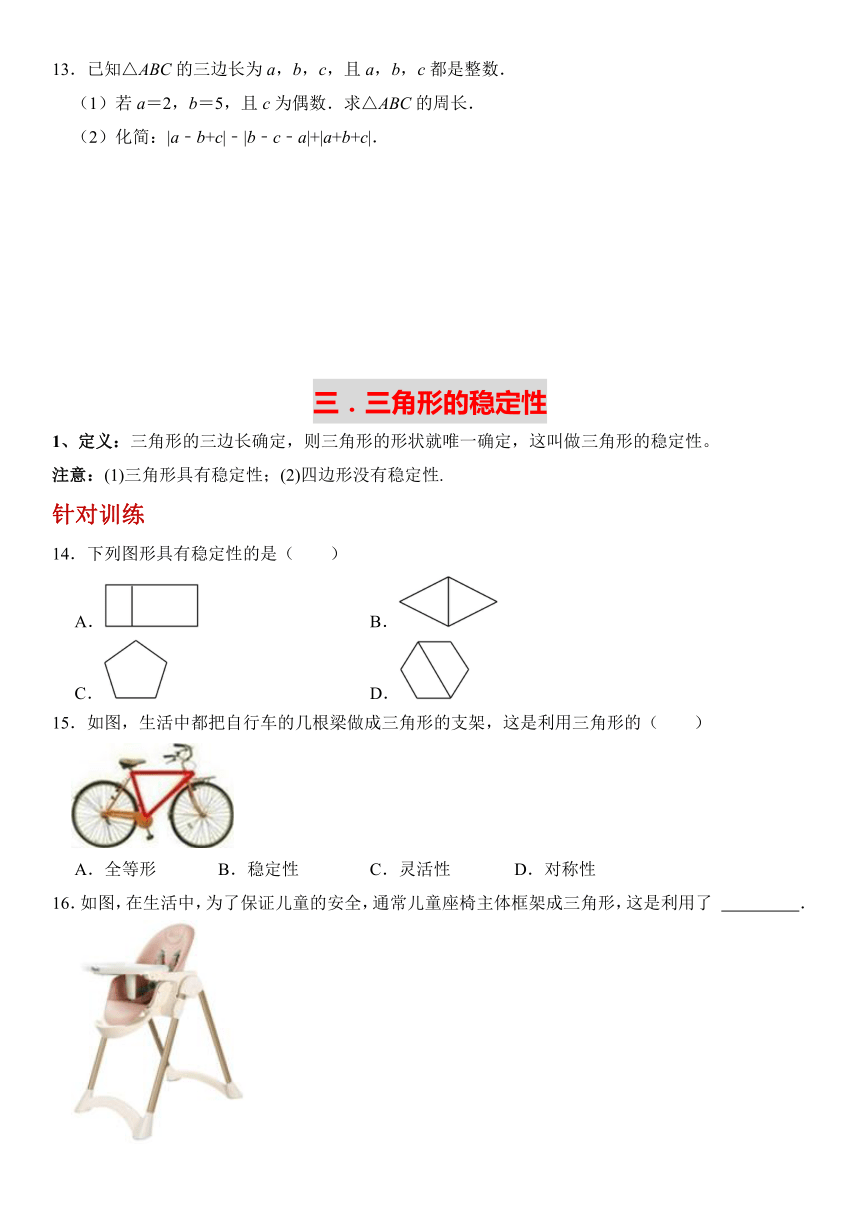
13.已知△ABC的三边长为a,b,c,且a,b,c都是整数.
(1)若a=2,b=5,且c为偶数.求△ABC的周长.
(2)化简:|a﹣b+c|﹣|b﹣c﹣a|+|a+b+c|.
三.三角形的稳定性
1、定义:三角形的三边长确定,则三角形的形状就唯一确定,这叫做三角形的稳定性。
注意:(1)三角形具有稳定性;(2)四边形没有稳定性.
针对训练
14.下列图形具有稳定性的是( )
A. B.
C. D.
15.如图,生活中都把自行车的几根梁做成三角形的支架,这是利用三角形的( )
A.全等形 B.稳定性 C.灵活性 D.对称性
16.如图,在生活中,为了保证儿童的安全,通常儿童座椅主体框架成三角形,这是利用了 .
17.如图,要使四边形木架(用四根木条钉成)不变形,至少要钉上几根木条?
四.三角形的角平分线、中线和高
1、中线:在三角形中,连接一个顶点和它对边的中点的线段叫做三角形的中线。由于三角形有三条边,所以一个三角形有三条中线。且三条中线交于一点。这点称为三角形的重心。每条三角形中线分得的两个三角形面积相等。
2、三角形的角平分线:三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点间的线段叫做三角形的角平分线。 三角形的角平分线不是角的平分线,是线段。角的平分线是射线。(这是三角形的角平分线与角平分线的区别)
3、高线:从三角形一个顶点向它的对边做垂线,顶点和垂足之间的线段叫做三角形的高线(简称三角形的高)。
针对训练
18.如图,四个图形中,线段BE是△ABC的高的图是( )
A. B.
C. D.
19.三角形一边上的中线把原三角形分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形
20.如图,△ABC中,AD⊥BC交BC的延长线于D点,BE⊥AC交AC的延长线于E,FC⊥BC,下列说法错误的是( )
A.AD是△ABC的高 B.BE是△ABC的高
C.BC是△BCF的高 D.线段CF长表示点C到直线AB的距离
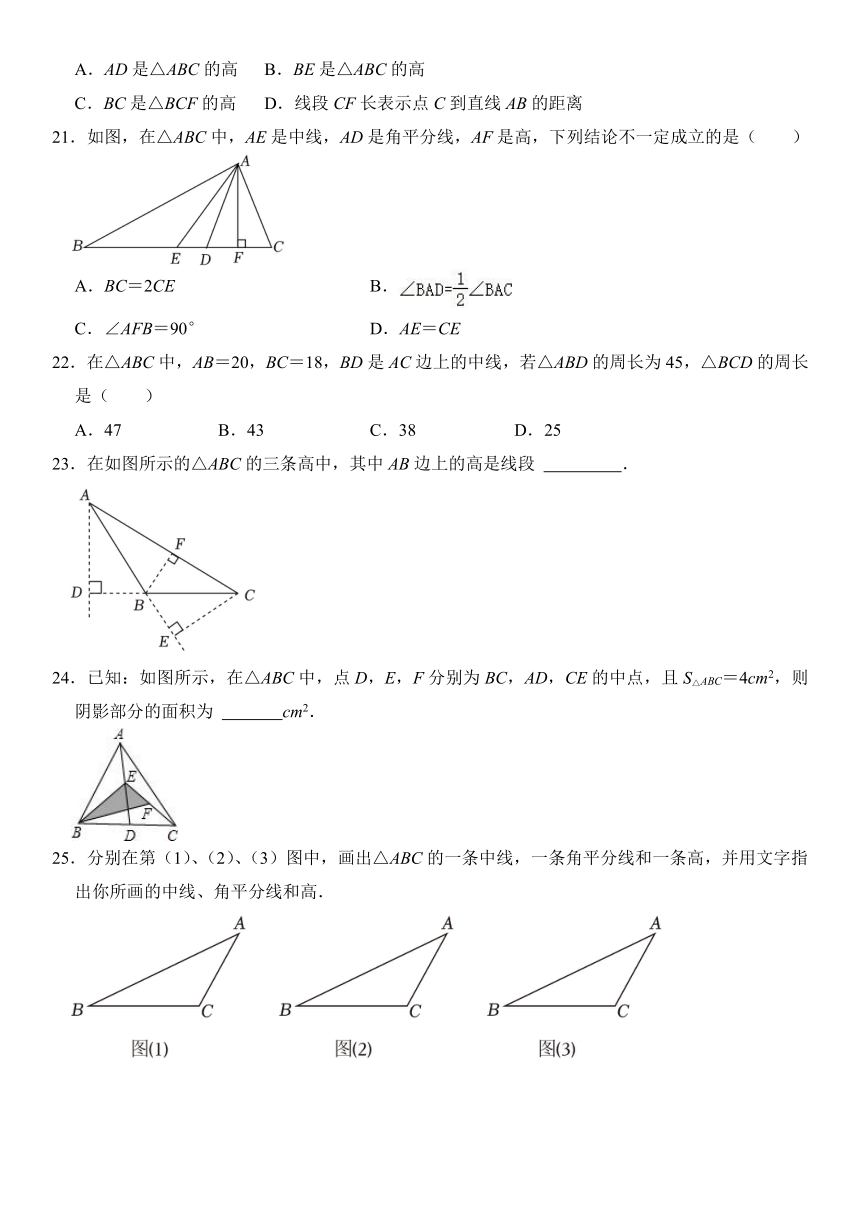
21.如图,在△ABC中,AE是中线,AD是角平分线,AF是高,下列结论不一定成立的是( )
A.BC=2CE B.
C.∠AFB=90° D.AE=CE
22.在△ABC中,AB=20,BC=18,BD是AC边上的中线,若△ABD的周长为45,△BCD的周长是( )
A.47 B.43 C.38 D.25
23.在如图所示的△ABC的三条高中,其中AB边上的高是线段 .
24.已知:如图所示,在△ABC中,点D,E,F分别为BC,AD,CE的中点,且S△ABC=4cm2,则阴影部分的面积为 cm2.
25.分别在第(1)、(2)、(3)图中,画出△ABC的一条中线,一条角平分线和一条高,并用文字指出你所画的中线、角平分线和高.
26.如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为13cm,求AC的长.
27.如图,AD是△ABC的高,CE是△ABC的角平分线,BF是△ABC的中线.
(1)若∠ACB=50°,∠BAD=65°,求∠AEC的度数;
(2)若AB=9,△BCF与△BAF的周长差为3,求BC的长.
参考答案
一.三角形的分类
1.解:从图中,只能看到一个角是锐角,其它的两个角中,可以都是锐角或有一个钝角或有一个直角.
故选:D.
2.解:三角形可分为不等边三角形和等腰三角形.
故选:D.
3.解:在△ABC中,若∠A:∠B:∠C=1:2:3,
∴设∠A=x,则∠B=2x,∠C=3x,
∴x+2x+3x=180°,
解得x=30°,
∴∠C=3x=90°,
∴此三角形是直角三角形.
故选:B.
4.解:以BE为边的三角形有△BEF,△BEC共2个.
故答案为:2.
5.解:1个三角形需要火柴棍3根,
2个三角形需要火柴棍5根,
3个三角形需要火柴棍7根,
…,
发现规律:n个三角形需要火柴棍2n+1根,
∴2n+1=41,
解得:n=20.
故答案为:20.
6.解:图中共有6个三角形,分别是△ABD,△ABE,△ACB,△ADE,△ADC,△AEC.
二.三角形的三边关系
7.解:A、1+2=3,不能组成三角形,故A不符合题意;
B、1+2<4,不能组成三角形,故B不符合题意;
C、2+2=4,不能组成三角形,故C不符合题意;
D、4+5>6,能组成三角形,故D符合题意.
故选:D.
8.解:∵AB=AC=2,
∴2﹣2<BC<2+2,即:0<BC<4,
故选:A.
9.解:由三角形三边关系定理得到:7﹣5<c<7+5,
∴2<c<12.
故选:C.
10.解:设第三边为x,则2<x<8,
∴x=3,4,5,6,7.
共有5种情形.
故答案为:5.
11.解:设第三边长为x,则
由三角形三边关系定理得3﹣2<x<3+2,即1<x<5.
∵第三边长为整数值,且△ABC是不等边三角形,
∴x的取值为4.
故答案为:4.
12.解:(1)∵|2a﹣b+2|+(a+b﹣8)2=0,
∴,
解得a=2,b=6,
∵6﹣2=4,6+2=8,
∴4<c<8,
∴c的取值范围为4<c<8;
(2)∵2x﹣c=1,
∴c=2x﹣1,
∴4<2x﹣1<8,
∴<x<,
∴x的取值范围为<x<.
13.解:(1)∵a=2,b=5,
∴5﹣2<c<5+2,
∴3<c<7,
∵c为偶数,
∴c=4或6,
当c=4时,△ABC的周长=a+b+c=2+5+4=11;
当c=6时,△ABC的周长=a+b+c=2+5+6=13,
综上所述,△ABC的周长为11或13;
(2)∵△ABC的边长为a,b,c,
∴a+c>b,
∴|a﹣b+c|﹣|b﹣c﹣a|+|a+b+c|
=a+c﹣b﹣(a+c﹣b)+a+b+c
=a+c﹣b﹣a﹣c+b+a+b+c
=a+b+c.
三.三角形的稳定性
14.解:所有图形里,只有三角形具有稳定性.
故选:B.
15.解:生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有稳定性.
故选:B.
16.解:儿童座椅主体框架成三角形,是利用三角形的稳定性,
故答案为:三角形的稳定性.
17.解:至少钉一根木条,即相对的两顶点钉一根木条就可以了.
四.三角形的角平分线、中线和高
18.解:由图可得,线段BE是△ABC的高的图是D选项.
故选:D.
19.解:三角形一边上的中线把原三角形分成两个面积相等的三角形.
故选:B.
20.解:A、AD是△ABC的高,说法正确,不符合题意;
B、BE是△ABC的高,说法正确,不符合题意;
C、BC是△BCF的高,说法正确,不符合题意;
D、线段CF长不能表示点C到直线AB的距离,故本选项说法错误,符合题意;
故选:D.
21.解:∵AE是中线,
∴BE=CE,
BC=2CE.
∴故选项A正确,不符合题意;
∵AF是高,
∴∠AFB=90°,故选项C正确,不符合题意;
∵AD是角平分线,
∴∠BAD=∠BAC.
故选项B正确,不符合题意;
根据题意不一定得出AE=CE,
故选项D不正确符合题意.
故选:D.
22.解:∵BD是AC边上的中线,
∴CD=AD,
∵△ABD的周长为45,
∴AB+AD+BD=45,
∵AB=20,
∴20+CD+BD=45,
∴CD+BD=25,
∵BC=18,
∴△BCD的周长=BC+CD+BD=18+25=43,
故选:B.
23.解:∵△ABC为钝角是三角形,CE⊥AE,
∴CE为AB边上的高.
故答案为:CE.
24.解:∵D为BC中点,根据同底等高的三角形面积相等,
∴S△ABD=S△ACD=S△ABC=×4=2(cm2),
同理S△BDE=S△CDE=S△BCE=×2=1(cm2),
∴S△BCE=2(cm2),
∵F为EC中点,
∴S△BEF=S△BCE=×2=1(cm2).
故答案为1.
25.解:如图AD为中线,AE为角平分线,AF为高
26.解:∵AD是BC边上的中线,
∴D为BC的中点,CD=BD.
∵△ADC的周长﹣△ABD的周长=5cm.
∴AC﹣AB=5cm.
又∵AB+AC=13cm,
∴AC=9cm.
即AC的长度是9cm.
27.解:(1)∵AD是△ABC的高,
∴∠ADB=90°,
∵∠BAD=65°,
∴∠ABD=90°﹣65°=25°,
∵CE是△ACB的角平分线,∠ACB=50°,
∴,
∴∠AEC=∠ABD+∠ECB=25°+25°=50°;
(2)∵F是AC中点,
∴AF=FC,
∵△BCF与△BAF的周长差为3,
∴(BC+CF+BF)﹣(AB+AF+BF)=3,
∴AB﹣BC=3,
∵AB=9,
∴BC=12.
11.1 与三角形有关的线段
一.三角形的分类
1、定义:由不在同一直线上的三条线段首尾顺次相接组成的图形叫做三角形。
2、三角形相关定义:三角形有三条边,三个内角,三个顶点.组成三角形的线段叫做三角形的边;相邻两边所组成的角叫做三角形的内角;相邻两边的公共端点是三角形的顶点。
3、符号表示:三角形ABC用符号表示为△ABC,三角形ABC的边AB可用边AB所对的角C的小写字母c表示,AC可用b表示,BC可用a表示.三个顶点用大写字母A,B,C来表示。
4、三角形根据不同的分类依据可分为不同类型:
①、按角分:1、锐角三角形;2、直角三角形;3、钝角三角形。
②、按边分:1、不等边三角形;2、等腰三角形;3、等边三角形(特殊等腰三角形)。
针对训练
1.图中的三角形被木板遮住了一部分,这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.以上都有可能
2.下列分类正确的是( )
A.三角形可分为等腰三角形、等边三角形
B.三角形可分为不等边三角形、等腰三角形以及等边三角形
C.三角形可分为不等边三角形和等边三角形
D.三角形可分为不等边三角形和等腰三角形
3.△ABC的三角之比是1:2:3,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.无法确定
4.如图,以BE为边的三角形有 个.
5.在一节数学活动课上,小敏同学用火柴棍拼成一排由三角形组成的图形,如图所示.按照这种方式继续拼下去,若图形中用了41根火柴棍,则图形中含有 个三角形.
6.图中有几个三角形?用符号表示这些三角形.
二.三角形的三边关系
1、三角形的三边关系:三角形的任意两边之和大于第三边;任意两边之差小于第三边.
注意:(1)三边关系的依据是:两点之间线段是短;
(2)围成三角形的条件是任意两边之和大于第三边.
针对训练
7.下列各组中的三条线段,能组成三角形的是( )
A.1,2,3 B.1,2,4 C.2,2,4 D.4,5,6
8.如图,人字梯的支架AB,AC的长度都为2米,则B,C两点之间的距离可能是( )
A.3米 B.4.2米 C.5米 D.6米
9.若三角形的两边长分别为5和7,则其第三边c的取值范围是( )
A.5<c<7 B.3≤c≤11 C.2<c<12 D.2≤c≤12
10.若一个三角形的边长均为整数,且两边长分别为3和5,则这样的三角形共有 个.
11.三边长不等的△ABC的两条边长分别为2和3,则且第三边长为整数值,则这个三角形的第三边长为 .
12.已知:a、b、c为△ABC的三边长,且a、b满足|2a﹣b+2|+(a+b﹣8)2=0.
(1)求c的取值范围;
(2)在(1)的条件下,若2x﹣c=1,求x的取值范围.
13.已知△ABC的三边长为a,b,c,且a,b,c都是整数.
(1)若a=2,b=5,且c为偶数.求△ABC的周长.
(2)化简:|a﹣b+c|﹣|b﹣c﹣a|+|a+b+c|.
三.三角形的稳定性
1、定义:三角形的三边长确定,则三角形的形状就唯一确定,这叫做三角形的稳定性。
注意:(1)三角形具有稳定性;(2)四边形没有稳定性.
针对训练
14.下列图形具有稳定性的是( )
A. B.
C. D.
15.如图,生活中都把自行车的几根梁做成三角形的支架,这是利用三角形的( )
A.全等形 B.稳定性 C.灵活性 D.对称性
16.如图,在生活中,为了保证儿童的安全,通常儿童座椅主体框架成三角形,这是利用了 .
17.如图,要使四边形木架(用四根木条钉成)不变形,至少要钉上几根木条?
四.三角形的角平分线、中线和高
1、中线:在三角形中,连接一个顶点和它对边的中点的线段叫做三角形的中线。由于三角形有三条边,所以一个三角形有三条中线。且三条中线交于一点。这点称为三角形的重心。每条三角形中线分得的两个三角形面积相等。
2、三角形的角平分线:三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点间的线段叫做三角形的角平分线。 三角形的角平分线不是角的平分线,是线段。角的平分线是射线。(这是三角形的角平分线与角平分线的区别)
3、高线:从三角形一个顶点向它的对边做垂线,顶点和垂足之间的线段叫做三角形的高线(简称三角形的高)。
针对训练
18.如图,四个图形中,线段BE是△ABC的高的图是( )
A. B.
C. D.
19.三角形一边上的中线把原三角形分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形
20.如图,△ABC中,AD⊥BC交BC的延长线于D点,BE⊥AC交AC的延长线于E,FC⊥BC,下列说法错误的是( )
A.AD是△ABC的高 B.BE是△ABC的高
C.BC是△BCF的高 D.线段CF长表示点C到直线AB的距离
21.如图,在△ABC中,AE是中线,AD是角平分线,AF是高,下列结论不一定成立的是( )
A.BC=2CE B.
C.∠AFB=90° D.AE=CE
22.在△ABC中,AB=20,BC=18,BD是AC边上的中线,若△ABD的周长为45,△BCD的周长是( )
A.47 B.43 C.38 D.25
23.在如图所示的△ABC的三条高中,其中AB边上的高是线段 .
24.已知:如图所示,在△ABC中,点D,E,F分别为BC,AD,CE的中点,且S△ABC=4cm2,则阴影部分的面积为 cm2.
25.分别在第(1)、(2)、(3)图中,画出△ABC的一条中线,一条角平分线和一条高,并用文字指出你所画的中线、角平分线和高.
26.如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为13cm,求AC的长.
27.如图,AD是△ABC的高,CE是△ABC的角平分线,BF是△ABC的中线.
(1)若∠ACB=50°,∠BAD=65°,求∠AEC的度数;
(2)若AB=9,△BCF与△BAF的周长差为3,求BC的长.
参考答案
一.三角形的分类
1.解:从图中,只能看到一个角是锐角,其它的两个角中,可以都是锐角或有一个钝角或有一个直角.
故选:D.
2.解:三角形可分为不等边三角形和等腰三角形.
故选:D.
3.解:在△ABC中,若∠A:∠B:∠C=1:2:3,
∴设∠A=x,则∠B=2x,∠C=3x,
∴x+2x+3x=180°,
解得x=30°,
∴∠C=3x=90°,
∴此三角形是直角三角形.
故选:B.
4.解:以BE为边的三角形有△BEF,△BEC共2个.
故答案为:2.
5.解:1个三角形需要火柴棍3根,
2个三角形需要火柴棍5根,
3个三角形需要火柴棍7根,
…,
发现规律:n个三角形需要火柴棍2n+1根,
∴2n+1=41,
解得:n=20.
故答案为:20.
6.解:图中共有6个三角形,分别是△ABD,△ABE,△ACB,△ADE,△ADC,△AEC.
二.三角形的三边关系
7.解:A、1+2=3,不能组成三角形,故A不符合题意;
B、1+2<4,不能组成三角形,故B不符合题意;
C、2+2=4,不能组成三角形,故C不符合题意;
D、4+5>6,能组成三角形,故D符合题意.
故选:D.
8.解:∵AB=AC=2,
∴2﹣2<BC<2+2,即:0<BC<4,
故选:A.
9.解:由三角形三边关系定理得到:7﹣5<c<7+5,
∴2<c<12.
故选:C.
10.解:设第三边为x,则2<x<8,
∴x=3,4,5,6,7.
共有5种情形.
故答案为:5.
11.解:设第三边长为x,则
由三角形三边关系定理得3﹣2<x<3+2,即1<x<5.
∵第三边长为整数值,且△ABC是不等边三角形,
∴x的取值为4.
故答案为:4.
12.解:(1)∵|2a﹣b+2|+(a+b﹣8)2=0,
∴,
解得a=2,b=6,
∵6﹣2=4,6+2=8,
∴4<c<8,
∴c的取值范围为4<c<8;
(2)∵2x﹣c=1,
∴c=2x﹣1,
∴4<2x﹣1<8,
∴<x<,
∴x的取值范围为<x<.
13.解:(1)∵a=2,b=5,
∴5﹣2<c<5+2,
∴3<c<7,
∵c为偶数,
∴c=4或6,
当c=4时,△ABC的周长=a+b+c=2+5+4=11;
当c=6时,△ABC的周长=a+b+c=2+5+6=13,
综上所述,△ABC的周长为11或13;
(2)∵△ABC的边长为a,b,c,
∴a+c>b,
∴|a﹣b+c|﹣|b﹣c﹣a|+|a+b+c|
=a+c﹣b﹣(a+c﹣b)+a+b+c
=a+c﹣b﹣a﹣c+b+a+b+c
=a+b+c.
三.三角形的稳定性
14.解:所有图形里,只有三角形具有稳定性.
故选:B.
15.解:生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有稳定性.
故选:B.
16.解:儿童座椅主体框架成三角形,是利用三角形的稳定性,
故答案为:三角形的稳定性.
17.解:至少钉一根木条,即相对的两顶点钉一根木条就可以了.
四.三角形的角平分线、中线和高
18.解:由图可得,线段BE是△ABC的高的图是D选项.
故选:D.
19.解:三角形一边上的中线把原三角形分成两个面积相等的三角形.
故选:B.
20.解:A、AD是△ABC的高,说法正确,不符合题意;
B、BE是△ABC的高,说法正确,不符合题意;
C、BC是△BCF的高,说法正确,不符合题意;
D、线段CF长不能表示点C到直线AB的距离,故本选项说法错误,符合题意;
故选:D.
21.解:∵AE是中线,
∴BE=CE,
BC=2CE.
∴故选项A正确,不符合题意;
∵AF是高,
∴∠AFB=90°,故选项C正确,不符合题意;
∵AD是角平分线,
∴∠BAD=∠BAC.
故选项B正确,不符合题意;
根据题意不一定得出AE=CE,
故选项D不正确符合题意.
故选:D.
22.解:∵BD是AC边上的中线,
∴CD=AD,
∵△ABD的周长为45,
∴AB+AD+BD=45,
∵AB=20,
∴20+CD+BD=45,
∴CD+BD=25,
∵BC=18,
∴△BCD的周长=BC+CD+BD=18+25=43,
故选:B.
23.解:∵△ABC为钝角是三角形,CE⊥AE,
∴CE为AB边上的高.
故答案为:CE.
24.解:∵D为BC中点,根据同底等高的三角形面积相等,
∴S△ABD=S△ACD=S△ABC=×4=2(cm2),
同理S△BDE=S△CDE=S△BCE=×2=1(cm2),
∴S△BCE=2(cm2),
∵F为EC中点,
∴S△BEF=S△BCE=×2=1(cm2).
故答案为1.
25.解:如图AD为中线,AE为角平分线,AF为高
26.解:∵AD是BC边上的中线,
∴D为BC的中点,CD=BD.
∵△ADC的周长﹣△ABD的周长=5cm.
∴AC﹣AB=5cm.
又∵AB+AC=13cm,
∴AC=9cm.
即AC的长度是9cm.
27.解:(1)∵AD是△ABC的高,
∴∠ADB=90°,
∵∠BAD=65°,
∴∠ABD=90°﹣65°=25°,
∵CE是△ACB的角平分线,∠ACB=50°,
∴,
∴∠AEC=∠ABD+∠ECB=25°+25°=50°;
(2)∵F是AC中点,
∴AF=FC,
∵△BCF与△BAF的周长差为3,
∴(BC+CF+BF)﹣(AB+AF+BF)=3,
∴AB﹣BC=3,
∵AB=9,
∴BC=12.
