最新华师版八上数学13. 2全等三角形的判定条件课件(21张PPT)
文档属性
| 名称 | 最新华师版八上数学13. 2全等三角形的判定条件课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 518.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-01 15:15:09 | ||
图片预览






文档简介
(共21张PPT)
华东师大版·八年级上册
1.全等三角形
2.全等三角形的判定条件
新课导入
下图中的几组图形有怎样的关系?
(1)
(2)
(3)
探究新知
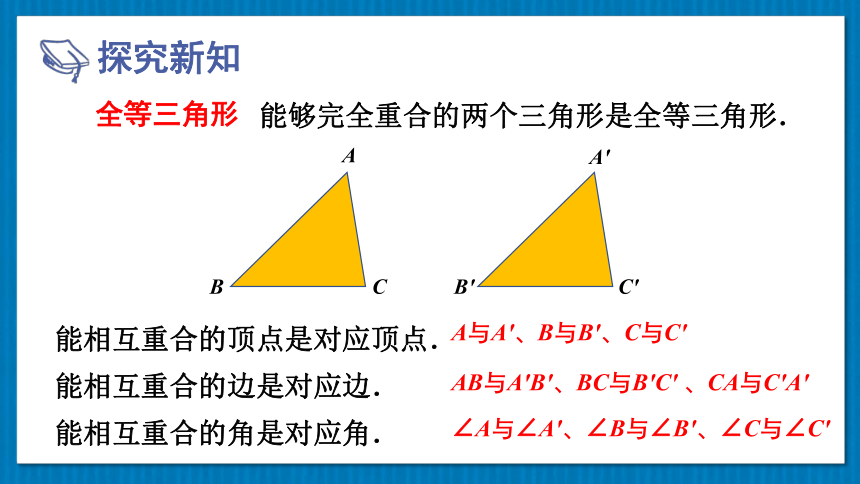
全等三角形
能够完全重合的两个三角形是全等三角形.
A
B
C
A′
B′
C′
能相互重合的顶点是对应顶点.
能相互重合的边是对应边.
能相互重合的角是对应角.
A与A′、B与B′、C与C′
AB与A′B′、BC与B′C′ 、CA与C′A′
∠A与∠A′、∠B与∠B′、∠C与∠C′
A
B
C
A′
B′
C′
全等三角形的性质:
全等三角形的对应边相等,对应角相等.
全等三角形的表示:
“全等”用符号“≌”来表示,读作“全等于”.
记两个三角形全等时,要把表示对应顶点的字母写在对应的位置上.
记作△ABC≌△A′B′C′
做
一
做
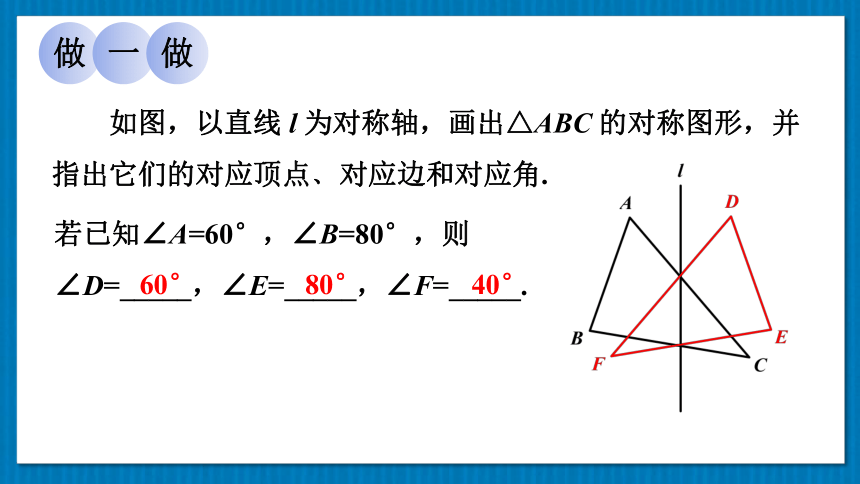
如图,以直线 l 为对称轴,画出△ABC 的对称图形,并指出它们的对应顶点﹑对应边和对应角.
若已知∠A=60°,∠B=80°,则
∠D=_____,∠E=_____,∠F=_____.
60°
80°
40°
1. 如图,将△ABC 绕点 B 按顺时针方向旋转 60°后得△A′BC′.指出对应顶点、对应边和对应角.
练习
解: 对应顶点: A 与A′,B 与B,C 与 C′;
对应边: AB 与 A′B,AC 与 A′C′,BC 与 BC′.
对应角:∠CBA 与∠C′BA′,∠A 与∠A′,
∠C 与∠C′.
【解析】∵ △ABC ≌ △DEF,
∴ ∠ACB = ∠DFE.
∴∠DFE = 180°-(∠A +∠B)=85°.
2. 如图,已知△ABC ≌△DEF,∠A =40°, ∠B =55°,则∠DFE 的度数是________.
85°
全等三角形的判定条件
对于全等三角形,从它的边、角来看,我们知道:若两个三角形的三条边与三个角都分别对应相等,那么这两个三角形一定可以互相重合,即全等.
能否再减少一些条件?对两个三角形来说?六个元素(三条边、三个角)中至少要有几个元素分别对应相等,这两个三角形才全等呢?
思考
探索
对应相等的元素
三角形是否全等
如果两个三角形只有一组对应相等的元素,那么会出现几种情况?这两个三角形会全等吗?
一条边
不一定
一个角
不一定
如果只知道两个三角形有一组对应相等的元素(边或角)﹐那么这两个三角形不一定全等.
探索
如果两个三角形有两组对应相等的元素,那么会出现几种可能的情况呢?这时,这两个三角形会全等吗?
由于一个三角形有三条边、三个角共六个元素,所以可能出现的情况会较多.可能的情况有:
_________________________________________
_________________________________________
两个角对应相等
两条边对应相等
一个角对应相等和一条边对应相等
如果只知道两个三角形有两组对应相等的元素(边或角),那么这两个三角形不一定全等.
试
一
试
分别按照下面的条件,用刻度尺或量角器画三角形,并和周围的同学比较一下,所画的图形是否全等.
(1)三角形的两个内角分别为 30°和 70°.
(2)三角形的两条边分别为 3 cm 和 5 cm.
(3)三角形的一个内角为 60°,一条边为 3 cm.
(i)这条长 3 cm 的边是 60°角的邻边;
(ii)这条长 3 cm 的边是 60°角的对边.
(1)三角形的两个内角分别为 30°和 70°.
(2)三角形的两条边分别为 3 cm 和 5 cm.
(3)三角形的一个内角为 60°,一条边为 3 cm.
(i)这条长 3 cm 的边是 60°角的邻边;
(ii)这条长 3 cm 的边是 60°角的对边.
你一定会发现,如果只知道两个三角形有两组对应相等的元素,那么这两个三角形是否全等的情况为:
对应相等的元素
三角形是否全等
两个角
不一定
两条边
不一定
一个角和一条边
不一定
由以上的探索与发现,我们知道两个三角形只有一组或两组对应相等的元素(边或角),那么这两个三角形不一定全等.
概括
三角都对应相等的三角形不一定全等.
如果两个三角形有三组对应相等的元素(边或角),又会如何呢?
三边都对应相等的三角形全等.
练 习
如图,将△AOB 绕点 O 旋转180°,得到△COD,这时△AOB≌△_____. 这两个三角形的对应边是:AO与______,OB与_______,BA与_______;
对应角是:∠AOB与_______,∠OBA与______,
∠BAO与________.
COD
CO
OD
DC
∠COD
∠ODC
∠DCO
2. 如图,AD // BC,AD = BC,AE⊥BC,将△ABE 沿
AD 方向平移,使点 A 与点 D 重合,点 E 平移至点 F,
则△ABE≌______,∠F =_____°.
△DCF
90
3. 如图,点 D 是△ABC 内一点,∠BAC = 90° ,AB = AC,将△ABD 绕点 A 逆时针旋转 90°,点 D 旋转至点 E,则△ABD≌______,AD=______,BD=______.
△ACE
AE
CE
课堂小结
全等三角形
定义
性质
1.全等三角形的对应边相等
2.全等三角形的对应角相等
探究三角形全等的条件
能够完全重合的两个三角形
1.一个元素(边或角)
两个三角形不一定全等
2.两个元素(边或角)
两个三角形不一定全等
3.三个元素(边或角)
两个三角形可能全等
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
华东师大版·八年级上册
1.全等三角形
2.全等三角形的判定条件
新课导入
下图中的几组图形有怎样的关系?
(1)
(2)
(3)
探究新知
全等三角形
能够完全重合的两个三角形是全等三角形.
A
B
C
A′
B′
C′
能相互重合的顶点是对应顶点.
能相互重合的边是对应边.
能相互重合的角是对应角.
A与A′、B与B′、C与C′
AB与A′B′、BC与B′C′ 、CA与C′A′
∠A与∠A′、∠B与∠B′、∠C与∠C′
A
B
C
A′
B′
C′
全等三角形的性质:
全等三角形的对应边相等,对应角相等.
全等三角形的表示:
“全等”用符号“≌”来表示,读作“全等于”.
记两个三角形全等时,要把表示对应顶点的字母写在对应的位置上.
记作△ABC≌△A′B′C′
做
一
做
如图,以直线 l 为对称轴,画出△ABC 的对称图形,并指出它们的对应顶点﹑对应边和对应角.
若已知∠A=60°,∠B=80°,则
∠D=_____,∠E=_____,∠F=_____.
60°
80°
40°
1. 如图,将△ABC 绕点 B 按顺时针方向旋转 60°后得△A′BC′.指出对应顶点、对应边和对应角.
练习
解: 对应顶点: A 与A′,B 与B,C 与 C′;
对应边: AB 与 A′B,AC 与 A′C′,BC 与 BC′.
对应角:∠CBA 与∠C′BA′,∠A 与∠A′,
∠C 与∠C′.
【解析】∵ △ABC ≌ △DEF,
∴ ∠ACB = ∠DFE.
∴∠DFE = 180°-(∠A +∠B)=85°.
2. 如图,已知△ABC ≌△DEF,∠A =40°, ∠B =55°,则∠DFE 的度数是________.
85°
全等三角形的判定条件
对于全等三角形,从它的边、角来看,我们知道:若两个三角形的三条边与三个角都分别对应相等,那么这两个三角形一定可以互相重合,即全等.
能否再减少一些条件?对两个三角形来说?六个元素(三条边、三个角)中至少要有几个元素分别对应相等,这两个三角形才全等呢?
思考
探索
对应相等的元素
三角形是否全等
如果两个三角形只有一组对应相等的元素,那么会出现几种情况?这两个三角形会全等吗?
一条边
不一定
一个角
不一定
如果只知道两个三角形有一组对应相等的元素(边或角)﹐那么这两个三角形不一定全等.
探索
如果两个三角形有两组对应相等的元素,那么会出现几种可能的情况呢?这时,这两个三角形会全等吗?
由于一个三角形有三条边、三个角共六个元素,所以可能出现的情况会较多.可能的情况有:
_________________________________________
_________________________________________
两个角对应相等
两条边对应相等
一个角对应相等和一条边对应相等
如果只知道两个三角形有两组对应相等的元素(边或角),那么这两个三角形不一定全等.
试
一
试
分别按照下面的条件,用刻度尺或量角器画三角形,并和周围的同学比较一下,所画的图形是否全等.
(1)三角形的两个内角分别为 30°和 70°.
(2)三角形的两条边分别为 3 cm 和 5 cm.
(3)三角形的一个内角为 60°,一条边为 3 cm.
(i)这条长 3 cm 的边是 60°角的邻边;
(ii)这条长 3 cm 的边是 60°角的对边.
(1)三角形的两个内角分别为 30°和 70°.
(2)三角形的两条边分别为 3 cm 和 5 cm.
(3)三角形的一个内角为 60°,一条边为 3 cm.
(i)这条长 3 cm 的边是 60°角的邻边;
(ii)这条长 3 cm 的边是 60°角的对边.
你一定会发现,如果只知道两个三角形有两组对应相等的元素,那么这两个三角形是否全等的情况为:
对应相等的元素
三角形是否全等
两个角
不一定
两条边
不一定
一个角和一条边
不一定
由以上的探索与发现,我们知道两个三角形只有一组或两组对应相等的元素(边或角),那么这两个三角形不一定全等.
概括
三角都对应相等的三角形不一定全等.
如果两个三角形有三组对应相等的元素(边或角),又会如何呢?
三边都对应相等的三角形全等.
练 习
如图,将△AOB 绕点 O 旋转180°,得到△COD,这时△AOB≌△_____. 这两个三角形的对应边是:AO与______,OB与_______,BA与_______;
对应角是:∠AOB与_______,∠OBA与______,
∠BAO与________.
COD
CO
OD
DC
∠COD
∠ODC
∠DCO
2. 如图,AD // BC,AD = BC,AE⊥BC,将△ABE 沿
AD 方向平移,使点 A 与点 D 重合,点 E 平移至点 F,
则△ABE≌______,∠F =_____°.
△DCF
90
3. 如图,点 D 是△ABC 内一点,∠BAC = 90° ,AB = AC,将△ABD 绕点 A 逆时针旋转 90°,点 D 旋转至点 E,则△ABD≌______,AD=______,BD=______.
△ACE
AE
CE
课堂小结
全等三角形
定义
性质
1.全等三角形的对应边相等
2.全等三角形的对应角相等
探究三角形全等的条件
能够完全重合的两个三角形
1.一个元素(边或角)
两个三角形不一定全等
2.两个元素(边或角)
两个三角形不一定全等
3.三个元素(边或角)
两个三角形可能全等
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
