最新华师版八年级上册数学第13章 全等三角形 章末复习课件(39张PPT)
文档属性
| 名称 | 最新华师版八年级上册数学第13章 全等三角形 章末复习课件(39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-01 00:00:00 | ||
图片预览











文档简介
(共39张PPT)
华东师大版·八年级数学上册
章末复习
知识结构
全等三角形
命题、定理与证明→命题、真命题、假命题、定理、证明
三角形全等的判定
S.A.S.、A.S.A.、A.A.S.、S.S.S.、H.L.
思路引导
已知两边
找夹角→S.A.S.
找直角→H.L.
找另一边→S.S.S.
已知两角
找夹边→A.S.A.
找对边→A.A.S.
已知一角一边
找夹角的另一边→S.A.S.
找夹边的另一角→A.S.A.
找边的对角或邻角→A.A.S.
直角三角形全等的判定→H.L.
知识结构
全等三角形
命题、定理与证明→命题、真命题、假命题、定理、证明
三角形全等的判定
S.A.S.、A.S.A.、A.A.S.、S.S.S.、H.L.
思路引导
已知两边
找夹角→S.A.S.
找直角→H.L.
找另一边→S.S.S.
已知两角
找夹边→A.S.A.
找对边→A.A.S.
已知一角一边
找夹角的另一边→S.A.S.
找夹边的另一角→A.S.A.
找边的对角或邻角→A.A.S.
直角三角形全等的判定→H.L.
等腰三角形
等腰三角形的性质与判定
等边三角形的性质与判定
尺规作图→作线段、作角、作角平分线、作垂线、作垂直平分线
逆命题与逆定理
互逆命题
互逆定理
线段垂直平分线的性质与判定
角平分线的性质与判定
整合归纳
这部分内容一般考查对命题真假的判定,将命题改写成“如果……,那么……”的形式,或写出已知命题的逆命题并判断真假,有时也会进行简单的推理论证.
1. 判断下列命题是真命题还是假命题,若是假命题,请举出反例说明:
(1)两直线平行,同旁内角互补;
(2)在同一平面内,垂直于同一条直线的两条直线平行;
(3)相等的角是内错角;
(4)有一个角是60°的三角形是等边三角形.
真命题
真命题
假命题,如:对顶角也相等
假命题,如:有60°、80°、40°的三角形不是等边三角形.
2.判断题(对的在括号内填“√”,错的在括号内填“×”)
(1)每个命题都有逆命题. ( )
(2)每个定理都有逆定理. ( )
(3)真命题的逆命题都是真命题. ( )
(4)假命题的逆命题都是假命题. ( )
√
×
×
×
3. 指出下列命题的条件和结论,写出它们的逆命题,并判断逆命题的真假.
(1)如果a+b<0,那么a<0,b<0 ;
条件: a+b<0.
结论: a<0,b<0.
逆命题:如果a<0,b<0,那么a+b<0.
真命题
3. 指出下列命题的条件和结论,写出它们的逆命题,并判断逆命题的真假.
(2)四个角相等的四边形是正方形.
条件:一个四边形的四个角相等.
结论:这个四边形是正方形.
逆命题:正方形的四个角相等.
真命题
全等三角形的性质与判定常用来解决一些计算或证明问题,涉及三角形、线段、角、图形面积等.全等三角形的性质: 全等三角形的对应元素相等. 全等三角形的判定方法:S.S.S.、S.A.S.、A.S.A.、A.A.S.、H.L.(只适用于直角三角形)
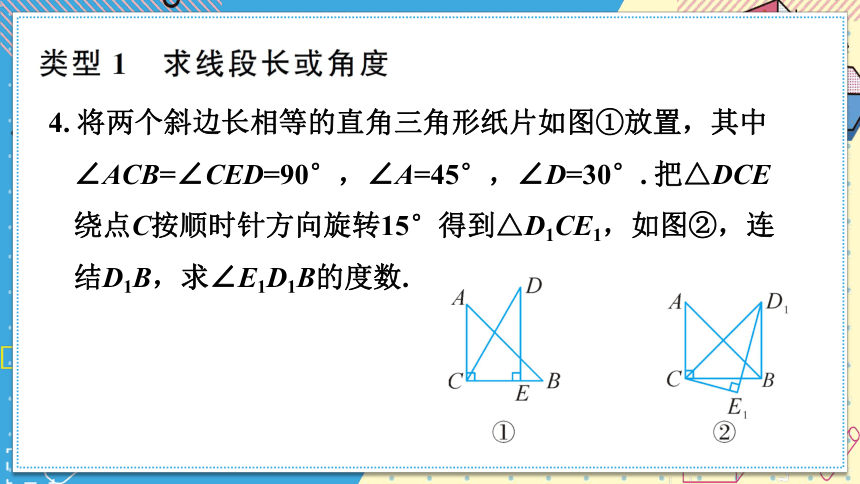
4. 将两个斜边长相等的直角三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°. 把△DCE绕点C按顺时针方向旋转15°得到△D1CE1,如图②,连结D1B,求∠E1D1B的度数.
解:∵∠CED=90°,∠D=30°,
∴∠DCE=60°.
∵△DCE绕点C按顺时针方向旋转15°,
∴∠BCE1=15°,
∴∠BCD1=60°-15°
=45°.
∴∠BCD1=∠A
在△ABC和△CD1B中,
∵AC=CB,∠A=∠BCD ,AB=CD1 ,
∴△ABC≌△CD1B(S.A.S.).
∴∠ABC=∠CD1B=45°.
∴∠E1D1B=∠BD1C-∠CD1E1
=45°-30°=15°
5. 如图,在△ABC和△ADE中,AC=AB,AE=AD,∠CAB =∠EAD = 90°,BD与CE交于点M,求证:(1)CE=BD;(2)CE⊥BD.
证明:(1)∵∠CAB=∠EAD=90°,
∴∠CAB+∠BAE=∠EAD+∠BAE,
即∠CAE=∠BAD.
5. 如图,在△ABC和△ADE中,AC=AB,AE=AD,∠CAB =∠EAD = 90°,BD与CE交于点M,求证:(1)CE=BD;(2)CE⊥BD.
在△ACE和△ABD中,
∵AC=AB,∠CAE=∠BAD,AE=AD,
∴△ACE≌△ABD.
∴CE=BD.
(2) ∵△ACE≌△ABD (已证),
∴ ∠ACE=∠ABD.
∵ ∠CAB+∠ACE=∠α=∠ABD+∠CMB,
∴ ∠CMB=∠CAB=90°
∴ CE⊥BD.
6. 如图,已知BE与CD相交于点A,M为BC的中点,∠1=∠2,AB=AC,求证:∠DBM=∠ECM.
证明:如图,连结MA.
∵ M为BC的中点﹐
∴BM=CM
在△ABM和△ACM中,
∵ AB=AC,BM=CM,AM=AM ,
∴△ABM≌△ACM(S.S.S.)
A
D
C
M
E
2
1
B
A
D
C
M
E
2
1
∴∠MAB=∠MAC,∠AMB=∠AMC.
∴∠DAM=∠EAM.
在△AMD和△AME中,
∵∠DAM=∠EAM,AM=AM,
∠AMD=∠AME,
∴△AMD≌△AME(A.S.A.)
∴MD=ME
B
∵∠1=∠2,∴∠AMD=∠AME.
A
D
C
M
E
2
1
在△MBD和△MCE中,
∴∠DBM=∠ECM.
∴△MBD≌△MCE(S.A.S.)
∴MD=ME
B
,∠1=∠2
,MB=MC,
本章中常用的作辅助线的方法有连结法、倍长中线法、截长补短法等,目的都是构造全等三角形,有时为了用角平分线的性质也要作垂线这种辅助线.
7. 如图,在四边形ABCD 中,AD =BC,AB=CD.求证:AB//CD,AD//BC.
A
B
C
D
证明:如图,连结AC.
在△ACD和△CAB中,
∵CD=AB,AC=CA ,AD=CB,
∴∠DCA=∠BAC,∠DAC=∠BCA.
∴AB//CD,AD//BC.
8. 如图,在△ABC中,AB=3,AC =4,AD是BC边上的中线,求AD的取值范围.
A
B
C
D
E
解:如图,延长AD到点E,使DE=AD,连结CE.
∵AD是BC边上的中线
∴BD=CD
在△ABD 和△ECD中,
∵BD=CD,∠ADB=∠EDC,AD=ED,
∴△ABD≌△ECD(S.A.S.).
∴AB=EC.
∵AB=3,AC =4,
∴4-3<AE<4+3,即 1<AE<7.
∵AE=2AD,∴0.5<AD<3.5.
A
B
C
D
E
等腰三角形和等边三角形都是特殊的三角形,且都有各自特殊的性质,在运用其性质或判定解决相关问题时要注意区别,结合图形具体分析,选择合适的方法解答.
9. 如图,在△ABC中,AB=AC,∠BAC = 36°,CD是∠ACB 的平分线且交AB于点D.
(1)求∠ADC的度数;
(2)过点A 作AE//BC,交CD的延长线于点E,试点E,试问△ADE是等腰三角形吗?问△ADE是等腰三角形吗
(1)求∠ADC的度数;
解:∵AB =AC, ∠BAC =36°,
∵CD 是∠ACB的平分线,
∴∠ADC=∠B+∠DCB=72°+36°=108°.
(2)过点A 作AE//BC,交CD的延长线于点E,试点E,试问△ADE是等腰三角形吗?问△ADE是等腰三角形吗
△ADE是等腰三角形.
理由:∵AE∥BC,∴∠EAB=∠B=72°.
∵∠ADC=108°,
∴∠ADE=180°-∠ADC=72°.
∴∠EAD=∠ADE,∴AE=AD,即△ADE是等腰三角形.
10. 如图,两个全等的等边三角形△ABC、△DEF的一边重叠地放在直线l上,AC、DE交于点P.
(1)判断△PCE的形状,并说明理由;
(1)解:△PCE是等边三角形.
∵△ABC、△DEF是全等的等边三角形,
∴∠EPC =180°-∠DEC-∠ACE
=180°-60°-60°
=60°
∴△PCE是等边三角形.
(2)求证:AF=DB.
(2)证明:∵△ACB 与△DEF是全等的等边三角形,
∴AC=DE,BC=EF,∠ACF=∠DEB=120°
∴BC-EC=EF-EC,即BE=FC.
在△AFC和△DBE中,
∵AC= DE,∠ACF=∠DEB,FC=BE,
∴△AFC≌△DBE(S.A.S.) ∴AF=DB.
五种基本作图分别是:①作一条线段等于已知线段;②作一个角等于已知角;③作已知角的平分线;④经过一已知点作已知直线的垂线;⑤作已知线段的垂直平分线.
11. 如图,某大学有A、B、C三栋教学楼,A、B在校内的主干道上,C在校内支路的末端. 为了方便教学和管理,现计划修建一栋办公楼P(位于∠ABC内部),使办公楼到公路AB、BC的距离相等,且到B、C两栋教学楼的距离也相等,请在图中作出办公楼P的位置.
(要求:尺规作图,不写已知、求作、作法和结论,保留作图痕迹,在所作图中标出Р的位置)
作出∠ABC的平分线,再作出BC的垂直平分线,交点即是P点位置.
角平分线的性质与判定常用来解决有关线段、角、面积等问题.线段垂直平分线的性质与判定常用来证明线段、角相等.
12. 如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE ⊥AB于点E,点F在AC上,BD=DF. 求证:(1)CF=EB ;
(2)AB=AF+2EB.
证明:(1)∵AD是∠BAC的平分线,DE⊥AB,DC ⊥AC,
∴DE=DC.
12. 如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE ⊥AB于点E,点F在AC上,BD=DF. 求证:(1)CF=EB ;
(2)AB=AF+2EB.
又∵BD=FD,
∴Rt△CDF≌Rt△EDB(H.L.).
∴CF=EB
(2)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴ED=CD.
∵AD=AD,
Rt△ADC≌Rt△ADE(H.L.)∴AC=AE.
由(1)得CF=EB,
∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.
13. 如图,AD是∠ABC 的角平分线,AD的垂直平分线交AB 于点F,交 BC的延长线于点E,连结DF、AE. 求证:
(1)∠EAD=∠EDA;
(2)DF∥AC.
证明:(1)∵EF是AD的垂直平分线,
∴AE=DE,∴∠EAD=∠EDA.
(2)∵EF为AD的垂直平分线,
∴FD=FA
∴∠FDA=∠FAD
∵AD平分∠BAC,
∴∠FAD=∠DAC,
∴∠FDA=∠DAC,
∴DF//AC.
课堂小结
通过本节课的复习,你还有哪些疑惑?
华东师大版·八年级数学上册
章末复习
知识结构
全等三角形
命题、定理与证明→命题、真命题、假命题、定理、证明
三角形全等的判定
S.A.S.、A.S.A.、A.A.S.、S.S.S.、H.L.
思路引导
已知两边
找夹角→S.A.S.
找直角→H.L.
找另一边→S.S.S.
已知两角
找夹边→A.S.A.
找对边→A.A.S.
已知一角一边
找夹角的另一边→S.A.S.
找夹边的另一角→A.S.A.
找边的对角或邻角→A.A.S.
直角三角形全等的判定→H.L.
知识结构
全等三角形
命题、定理与证明→命题、真命题、假命题、定理、证明
三角形全等的判定
S.A.S.、A.S.A.、A.A.S.、S.S.S.、H.L.
思路引导
已知两边
找夹角→S.A.S.
找直角→H.L.
找另一边→S.S.S.
已知两角
找夹边→A.S.A.
找对边→A.A.S.
已知一角一边
找夹角的另一边→S.A.S.
找夹边的另一角→A.S.A.
找边的对角或邻角→A.A.S.
直角三角形全等的判定→H.L.
等腰三角形
等腰三角形的性质与判定
等边三角形的性质与判定
尺规作图→作线段、作角、作角平分线、作垂线、作垂直平分线
逆命题与逆定理
互逆命题
互逆定理
线段垂直平分线的性质与判定
角平分线的性质与判定
整合归纳
这部分内容一般考查对命题真假的判定,将命题改写成“如果……,那么……”的形式,或写出已知命题的逆命题并判断真假,有时也会进行简单的推理论证.
1. 判断下列命题是真命题还是假命题,若是假命题,请举出反例说明:
(1)两直线平行,同旁内角互补;
(2)在同一平面内,垂直于同一条直线的两条直线平行;
(3)相等的角是内错角;
(4)有一个角是60°的三角形是等边三角形.
真命题
真命题
假命题,如:对顶角也相等
假命题,如:有60°、80°、40°的三角形不是等边三角形.
2.判断题(对的在括号内填“√”,错的在括号内填“×”)
(1)每个命题都有逆命题. ( )
(2)每个定理都有逆定理. ( )
(3)真命题的逆命题都是真命题. ( )
(4)假命题的逆命题都是假命题. ( )
√
×
×
×
3. 指出下列命题的条件和结论,写出它们的逆命题,并判断逆命题的真假.
(1)如果a+b<0,那么a<0,b<0 ;
条件: a+b<0.
结论: a<0,b<0.
逆命题:如果a<0,b<0,那么a+b<0.
真命题
3. 指出下列命题的条件和结论,写出它们的逆命题,并判断逆命题的真假.
(2)四个角相等的四边形是正方形.
条件:一个四边形的四个角相等.
结论:这个四边形是正方形.
逆命题:正方形的四个角相等.
真命题
全等三角形的性质与判定常用来解决一些计算或证明问题,涉及三角形、线段、角、图形面积等.全等三角形的性质: 全等三角形的对应元素相等. 全等三角形的判定方法:S.S.S.、S.A.S.、A.S.A.、A.A.S.、H.L.(只适用于直角三角形)
4. 将两个斜边长相等的直角三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°. 把△DCE绕点C按顺时针方向旋转15°得到△D1CE1,如图②,连结D1B,求∠E1D1B的度数.
解:∵∠CED=90°,∠D=30°,
∴∠DCE=60°.
∵△DCE绕点C按顺时针方向旋转15°,
∴∠BCE1=15°,
∴∠BCD1=60°-15°
=45°.
∴∠BCD1=∠A
在△ABC和△CD1B中,
∵AC=CB,∠A=∠BCD ,AB=CD1 ,
∴△ABC≌△CD1B(S.A.S.).
∴∠ABC=∠CD1B=45°.
∴∠E1D1B=∠BD1C-∠CD1E1
=45°-30°=15°
5. 如图,在△ABC和△ADE中,AC=AB,AE=AD,∠CAB =∠EAD = 90°,BD与CE交于点M,求证:(1)CE=BD;(2)CE⊥BD.
证明:(1)∵∠CAB=∠EAD=90°,
∴∠CAB+∠BAE=∠EAD+∠BAE,
即∠CAE=∠BAD.
5. 如图,在△ABC和△ADE中,AC=AB,AE=AD,∠CAB =∠EAD = 90°,BD与CE交于点M,求证:(1)CE=BD;(2)CE⊥BD.
在△ACE和△ABD中,
∵AC=AB,∠CAE=∠BAD,AE=AD,
∴△ACE≌△ABD.
∴CE=BD.
(2) ∵△ACE≌△ABD (已证),
∴ ∠ACE=∠ABD.
∵ ∠CAB+∠ACE=∠α=∠ABD+∠CMB,
∴ ∠CMB=∠CAB=90°
∴ CE⊥BD.
6. 如图,已知BE与CD相交于点A,M为BC的中点,∠1=∠2,AB=AC,求证:∠DBM=∠ECM.
证明:如图,连结MA.
∵ M为BC的中点﹐
∴BM=CM
在△ABM和△ACM中,
∵ AB=AC,BM=CM,AM=AM ,
∴△ABM≌△ACM(S.S.S.)
A
D
C
M
E
2
1
B
A
D
C
M
E
2
1
∴∠MAB=∠MAC,∠AMB=∠AMC.
∴∠DAM=∠EAM.
在△AMD和△AME中,
∵∠DAM=∠EAM,AM=AM,
∠AMD=∠AME,
∴△AMD≌△AME(A.S.A.)
∴MD=ME
B
∵∠1=∠2,∴∠AMD=∠AME.
A
D
C
M
E
2
1
在△MBD和△MCE中,
∴∠DBM=∠ECM.
∴△MBD≌△MCE(S.A.S.)
∴MD=ME
B
,∠1=∠2
,MB=MC,
本章中常用的作辅助线的方法有连结法、倍长中线法、截长补短法等,目的都是构造全等三角形,有时为了用角平分线的性质也要作垂线这种辅助线.
7. 如图,在四边形ABCD 中,AD =BC,AB=CD.求证:AB//CD,AD//BC.
A
B
C
D
证明:如图,连结AC.
在△ACD和△CAB中,
∵CD=AB,AC=CA ,AD=CB,
∴∠DCA=∠BAC,∠DAC=∠BCA.
∴AB//CD,AD//BC.
8. 如图,在△ABC中,AB=3,AC =4,AD是BC边上的中线,求AD的取值范围.
A
B
C
D
E
解:如图,延长AD到点E,使DE=AD,连结CE.
∵AD是BC边上的中线
∴BD=CD
在△ABD 和△ECD中,
∵BD=CD,∠ADB=∠EDC,AD=ED,
∴△ABD≌△ECD(S.A.S.).
∴AB=EC.
∵AB=3,AC =4,
∴4-3<AE<4+3,即 1<AE<7.
∵AE=2AD,∴0.5<AD<3.5.
A
B
C
D
E
等腰三角形和等边三角形都是特殊的三角形,且都有各自特殊的性质,在运用其性质或判定解决相关问题时要注意区别,结合图形具体分析,选择合适的方法解答.
9. 如图,在△ABC中,AB=AC,∠BAC = 36°,CD是∠ACB 的平分线且交AB于点D.
(1)求∠ADC的度数;
(2)过点A 作AE//BC,交CD的延长线于点E,试点E,试问△ADE是等腰三角形吗?问△ADE是等腰三角形吗
(1)求∠ADC的度数;
解:∵AB =AC, ∠BAC =36°,
∵CD 是∠ACB的平分线,
∴∠ADC=∠B+∠DCB=72°+36°=108°.
(2)过点A 作AE//BC,交CD的延长线于点E,试点E,试问△ADE是等腰三角形吗?问△ADE是等腰三角形吗
△ADE是等腰三角形.
理由:∵AE∥BC,∴∠EAB=∠B=72°.
∵∠ADC=108°,
∴∠ADE=180°-∠ADC=72°.
∴∠EAD=∠ADE,∴AE=AD,即△ADE是等腰三角形.
10. 如图,两个全等的等边三角形△ABC、△DEF的一边重叠地放在直线l上,AC、DE交于点P.
(1)判断△PCE的形状,并说明理由;
(1)解:△PCE是等边三角形.
∵△ABC、△DEF是全等的等边三角形,
∴∠EPC =180°-∠DEC-∠ACE
=180°-60°-60°
=60°
∴△PCE是等边三角形.
(2)求证:AF=DB.
(2)证明:∵△ACB 与△DEF是全等的等边三角形,
∴AC=DE,BC=EF,∠ACF=∠DEB=120°
∴BC-EC=EF-EC,即BE=FC.
在△AFC和△DBE中,
∵AC= DE,∠ACF=∠DEB,FC=BE,
∴△AFC≌△DBE(S.A.S.) ∴AF=DB.
五种基本作图分别是:①作一条线段等于已知线段;②作一个角等于已知角;③作已知角的平分线;④经过一已知点作已知直线的垂线;⑤作已知线段的垂直平分线.
11. 如图,某大学有A、B、C三栋教学楼,A、B在校内的主干道上,C在校内支路的末端. 为了方便教学和管理,现计划修建一栋办公楼P(位于∠ABC内部),使办公楼到公路AB、BC的距离相等,且到B、C两栋教学楼的距离也相等,请在图中作出办公楼P的位置.
(要求:尺规作图,不写已知、求作、作法和结论,保留作图痕迹,在所作图中标出Р的位置)
作出∠ABC的平分线,再作出BC的垂直平分线,交点即是P点位置.
角平分线的性质与判定常用来解决有关线段、角、面积等问题.线段垂直平分线的性质与判定常用来证明线段、角相等.
12. 如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE ⊥AB于点E,点F在AC上,BD=DF. 求证:(1)CF=EB ;
(2)AB=AF+2EB.
证明:(1)∵AD是∠BAC的平分线,DE⊥AB,DC ⊥AC,
∴DE=DC.
12. 如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE ⊥AB于点E,点F在AC上,BD=DF. 求证:(1)CF=EB ;
(2)AB=AF+2EB.
又∵BD=FD,
∴Rt△CDF≌Rt△EDB(H.L.).
∴CF=EB
(2)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴ED=CD.
∵AD=AD,
Rt△ADC≌Rt△ADE(H.L.)∴AC=AE.
由(1)得CF=EB,
∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.
13. 如图,AD是∠ABC 的角平分线,AD的垂直平分线交AB 于点F,交 BC的延长线于点E,连结DF、AE. 求证:
(1)∠EAD=∠EDA;
(2)DF∥AC.
证明:(1)∵EF是AD的垂直平分线,
∴AE=DE,∴∠EAD=∠EDA.
(2)∵EF为AD的垂直平分线,
∴FD=FA
∴∠FDA=∠FAD
∵AD平分∠BAC,
∴∠FAD=∠DAC,
∴∠FDA=∠DAC,
∴DF//AC.
课堂小结
通过本节课的复习,你还有哪些疑惑?
