最新华师版八年级上册数学 第13章 全等三角形-章末复习课件(23张PPT)
文档属性
| 名称 | 最新华师版八年级上册数学 第13章 全等三角形-章末复习课件(23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-01 15:47:56 | ||
图片预览



文档简介
(共23张PPT)
华东师大版·八年级数学上册
复习题
1. 判断下列命题是真命题还是假命题,若是假命题,请举出反例说明:
(1)两直线平行,同旁内角互补;
(2)在同一平面内,垂直于同一条直线的两条直线平行;
(3)相等的角是内错角;
(4)有一个角是60°的三角形是等边三角形.
真命题
真命题
假命题,如:对顶角也相等
假命题,如:有60°、80°、40°的三角形不是等边三角形.
2.判断题(对的在括号内填“√”,错的在括号内填“×”)
(1)每个命题都有逆命题. ( )
(2)每个定理都有逆定理. ( )
(3)真命题的逆命题都是真命题. ( )
(4)假命题的逆命题都是假命题. ( )
√
×
×
×
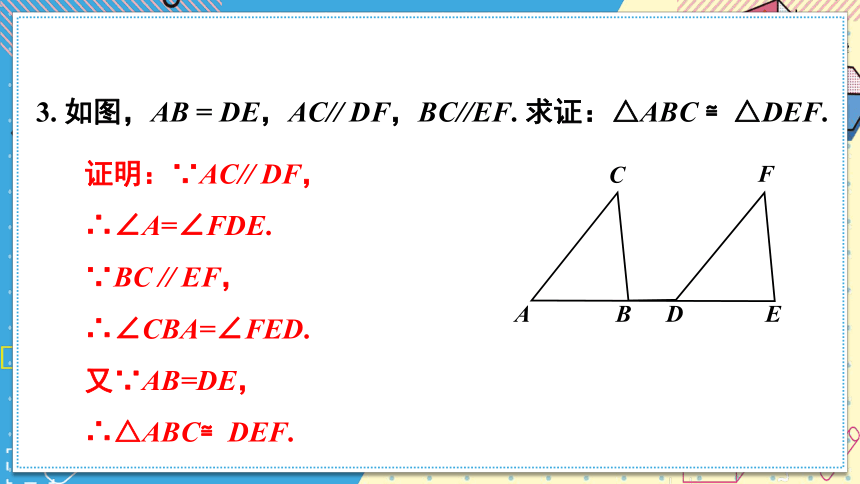
3. 如图,AB = DE,AC// DF,BC//EF. 求证:△ABC ≌△DEF.
证明:∵AC// DF,
∴∠A=∠FDE.
∵BC // EF,
∴∠CBA=∠FED.
又∵AB=DE,
∴△ABC≌DEF.
A
B
D
E
F
C
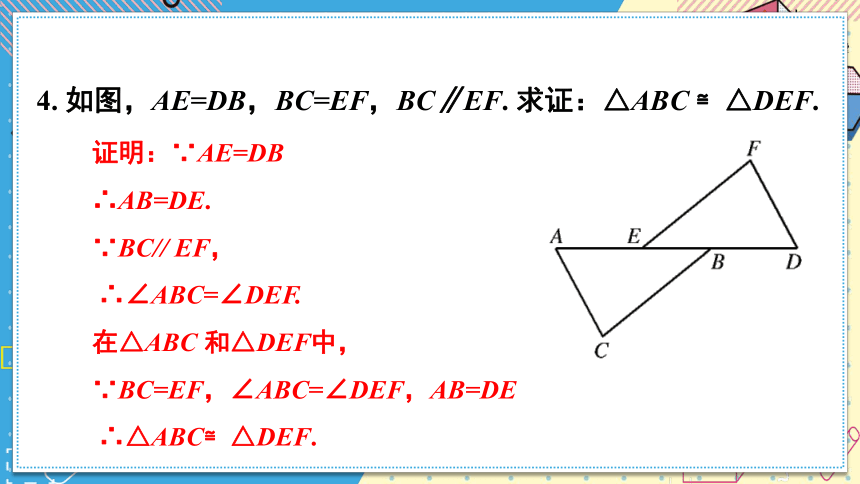
4. 如图,AE=DB,BC=EF,BC∥EF. 求证:△ABC ≌△DEF.
证明:∵AE=DB
∴AB=DE.
∵BC// EF,
∴∠ABC=∠DEF.
在△ABC 和△DEF中,
∵BC=EF,∠ABC=∠DEF,AB=DE
∴△ABC≌△DEF.
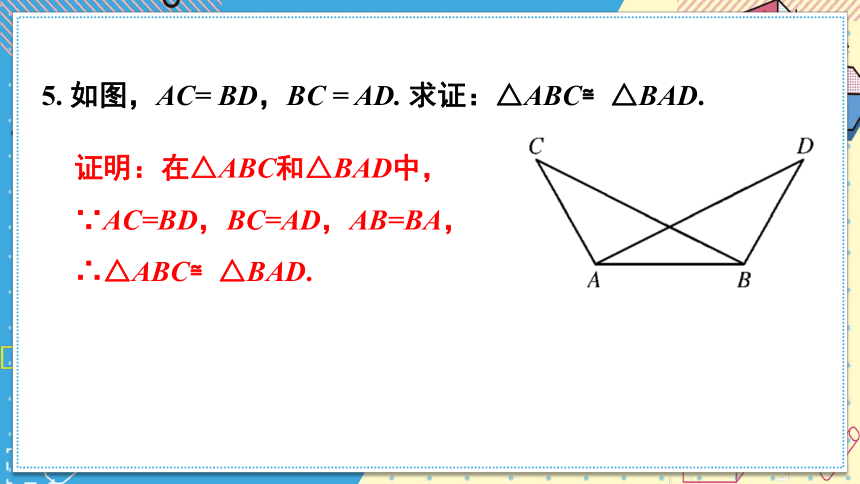
5. 如图,AC= BD,BC = AD. 求证:△ABC≌△BAD.
证明:在△ABC和△BAD中,
∵AC=BD,BC=AD,AB=BA,
∴△ABC≌△BAD.
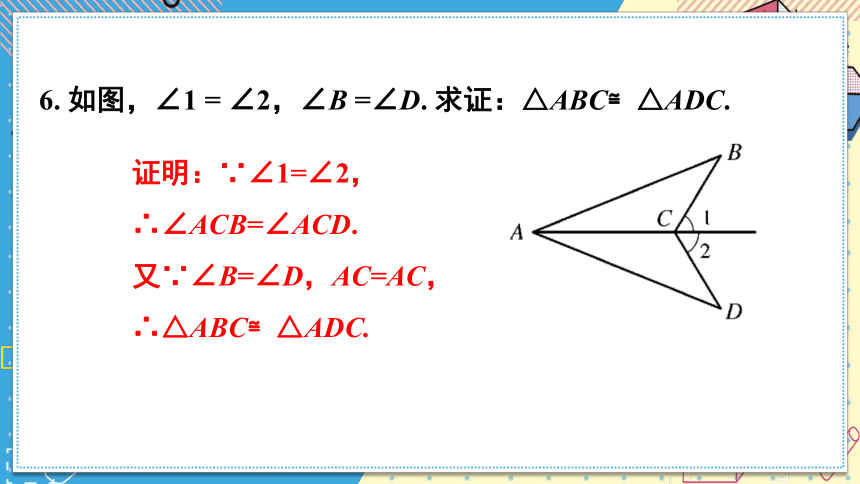
6. 如图,∠1 = ∠2,∠B =∠D. 求证:△ABC≌△ADC.
证明:∵∠1=∠2,
∴∠ACB=∠ACD.
又∵∠B=∠D,AC=AC,
∴△ABC≌△ADC.
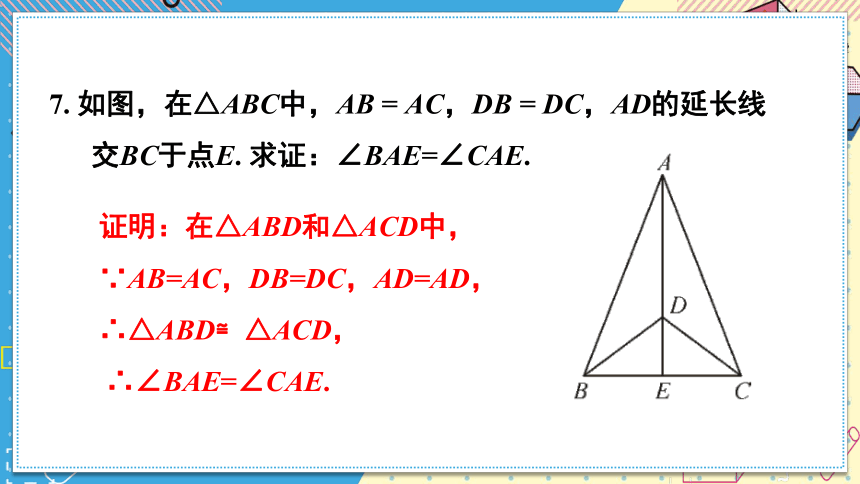
7. 如图,在△ABC中,AB = AC,DB = DC,AD的延长线交BC于点E. 求证:∠BAE=∠CAE.
证明:在△ABD和△ACD中,
∵AB=AC,DB=DC,AD=AD,
∴△ABD≌△ACD,
∴∠BAE=∠CAE.
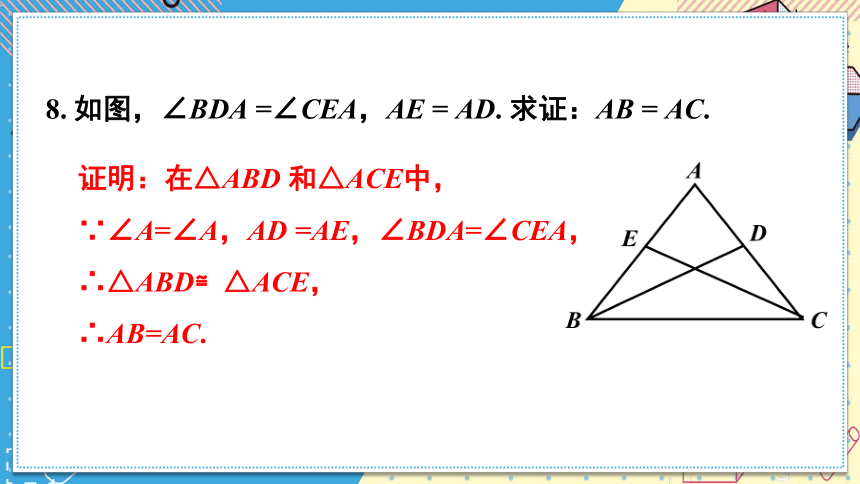
8. 如图,∠BDA =∠CEA,AE = AD. 求证:AB = AC.
证明:在△ABD 和△ACE中,
∵∠A=∠A,AD =AE,∠BDA=∠CEA,
∴△ABD≌△ACE,
∴AB=AC.
9. 如图,∠ACB = 90°,AC = AD,DE ⊥AB. 求证:∠ECD =∠EDC.
证明:∵DE⊥AB,
∴∠ADE=∠ADC+∠EDC=90°.
∵AC=AD,
∴∠ACD=∠ADC.
又∵∠ACB=∠ACD+∠DCE=90°,
∴∠ECD=∠EDC.
A
B
C
D
E
10. 如图,要测量河岸相对的两点A、B间的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再定出BF的垂线DE,使点A、C、E在同一条直线上,测得的DE的长就是AB的长,为什么?
解:∵AB⊥BC,DE⊥BC,
∴∠ABC=∠EDC.
在△ABC和△EDC中,
∵∠ABC= ∠EDC,BC= DC,∠ACB=∠ECD,
∴△ABC≌△EDC,
∴AB=ED.
11. 如图,在△ABC中,∠A = 120°,AB = AC,D是BC边的中点,DE⊥AB,DF⊥AC,点E、F为垂足. 求证:△DEF是等边三角形.
证明:连接AD,
∵AB=AC,D是BC中点,
∴AD平分∠BAC,
又∵DE⊥AB,DF⊥AC,
∴DE=DF.
11. 如图,在△ABC中,∠A = 120°,AB = AC,D是BC边的中点,DE⊥AB,DF⊥AC,点E、F为垂足. 求证:△DEF是等边三角形.
∵∠A=120°,AB=AC,
∴∠B=∠C=30°,
∴∠BDE=∠CDF=60°,
∴∠EDF=180°-(∠BDE+∠CDF)=60°
∴ △DEF是等边三角形.
12. 如图,在△ABC中,∠C = 90°,∠A = 36°,DE是线段AB的垂直平分线,交AB于点D,交AC于点E. 求证:∠EBC=18°.
证明:∵∠C=90°,∠A=36°,
∴∠ABC=54°.
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠A=∠EBA=36°,
∴∠EBC=∠ABC-∠EBA=18°.
A
B
C
D
E
13. 如图,AB = AD,AC = AE,∠BAE = ∠DAC. 求证:∠C = ∠E.
证明:∵∠BAE=∠DAC,
∴∠BAE+∠EAC=∠DAC+∠EAC,
即∠BAC=∠DAE.
在△BAC和△DAE 中,
∵AB =AD,∠BAC=∠DAE,AC=AE,
∴△BAC≌△DAE,
∴∠C=∠E.
A
B
C
D
E
14. 如图,BF⊥AC,CE⊥AB,BE = CF,BF与CE交于点D. 求证:AD平分∠BAC.
证明:∵BF⊥AC,CE⊥AB,
∴∠ BED=∠CFD=90°.
在△BED和△CFD中,
∵∠BED=∠CFD,∠EDB=∠FDC,BE=CF,
∴△BED≌△CFD,
∴DE=DF.
又∵BF⊥AC,CE⊥AB,
∴AD 平分∠BAC.
15. 如图,AD=BC,∠ADC = ∠BCD. 求证:∠BAC = ∠ABD.
证明:∵在△ADC和△BCD中,
∵AD=BC,∠ADC=∠BCD,DC=CD,
∴△ADC≌△BCD,.
∴AC=BD.
在△ABD和△BAC中,
∵AD=BC,AB= BA,AC=BD,
∴△ABD≌△BAC,
∴∠BAC=∠ABD.
16. 如图,已知△ABC,求作点P,使AP=CP,且点P到边BA、BC的距离相等.
提示:作 AC的垂直平分线和∠ABC的平分线,交点即为点P.
17.两个直角三角形有两个角及一条边分别相等,这两个直角三角形会全等吗?试列出各种情况,并一一加以说明.
不一定.①当直角和一锐角相等,一条边是斜边或锐角的对边或两角的夹边对应相等,这两个三角形全等. ②当直角和一锐角相等,一个三角形的斜边和另一个三角形的直角边相等或一个三角形的锐角的邻边和另一个三角形锐角的对边相等,它们不全等.
18.如图,已知Rt△ABC≌Rt△ADE,∠ABC = ∠ADE = 90°, BC与DE相交于点F,连结CD、EB.
(1)请找出图中其他的全等三角形;
(2)试证明CF = EF.
(1)△ADC≌△ABE;
△CDF≌△EBF ;
(2)证明:连结CE.
∵Rt△ABC≌Rt△ADE,
∴AC=AE,∠ACB=∠AED,
∴∠ACE=∠AEC,
∠ACE-∠ACB=∠AEC-∠AED,
即∠BCE=∠DEC,
∴CF=EF
19.如图,在△ABC 与△ABD中,AD与BC相交于点O,∠1 = ∠2,请你添加一个条件(不再添加其他线段,不再标注或使用其他字母),使AC = BD,并给出证明.
你添加的条件是:_________________.
∠C=∠D
证明:∵∠1=∠2,
∴OA =OB.
在△AOC和△BOD 中,
∵∠C=∠D, ∠COA=∠DOB,OA=OB
∴△AOC≌△BOD,∴AC=BD.
华东师大版·八年级数学上册
复习题
1. 判断下列命题是真命题还是假命题,若是假命题,请举出反例说明:
(1)两直线平行,同旁内角互补;
(2)在同一平面内,垂直于同一条直线的两条直线平行;
(3)相等的角是内错角;
(4)有一个角是60°的三角形是等边三角形.
真命题
真命题
假命题,如:对顶角也相等
假命题,如:有60°、80°、40°的三角形不是等边三角形.
2.判断题(对的在括号内填“√”,错的在括号内填“×”)
(1)每个命题都有逆命题. ( )
(2)每个定理都有逆定理. ( )
(3)真命题的逆命题都是真命题. ( )
(4)假命题的逆命题都是假命题. ( )
√
×
×
×
3. 如图,AB = DE,AC// DF,BC//EF. 求证:△ABC ≌△DEF.
证明:∵AC// DF,
∴∠A=∠FDE.
∵BC // EF,
∴∠CBA=∠FED.
又∵AB=DE,
∴△ABC≌DEF.
A
B
D
E
F
C
4. 如图,AE=DB,BC=EF,BC∥EF. 求证:△ABC ≌△DEF.
证明:∵AE=DB
∴AB=DE.
∵BC// EF,
∴∠ABC=∠DEF.
在△ABC 和△DEF中,
∵BC=EF,∠ABC=∠DEF,AB=DE
∴△ABC≌△DEF.
5. 如图,AC= BD,BC = AD. 求证:△ABC≌△BAD.
证明:在△ABC和△BAD中,
∵AC=BD,BC=AD,AB=BA,
∴△ABC≌△BAD.
6. 如图,∠1 = ∠2,∠B =∠D. 求证:△ABC≌△ADC.
证明:∵∠1=∠2,
∴∠ACB=∠ACD.
又∵∠B=∠D,AC=AC,
∴△ABC≌△ADC.
7. 如图,在△ABC中,AB = AC,DB = DC,AD的延长线交BC于点E. 求证:∠BAE=∠CAE.
证明:在△ABD和△ACD中,
∵AB=AC,DB=DC,AD=AD,
∴△ABD≌△ACD,
∴∠BAE=∠CAE.
8. 如图,∠BDA =∠CEA,AE = AD. 求证:AB = AC.
证明:在△ABD 和△ACE中,
∵∠A=∠A,AD =AE,∠BDA=∠CEA,
∴△ABD≌△ACE,
∴AB=AC.
9. 如图,∠ACB = 90°,AC = AD,DE ⊥AB. 求证:∠ECD =∠EDC.
证明:∵DE⊥AB,
∴∠ADE=∠ADC+∠EDC=90°.
∵AC=AD,
∴∠ACD=∠ADC.
又∵∠ACB=∠ACD+∠DCE=90°,
∴∠ECD=∠EDC.
A
B
C
D
E
10. 如图,要测量河岸相对的两点A、B间的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再定出BF的垂线DE,使点A、C、E在同一条直线上,测得的DE的长就是AB的长,为什么?
解:∵AB⊥BC,DE⊥BC,
∴∠ABC=∠EDC.
在△ABC和△EDC中,
∵∠ABC= ∠EDC,BC= DC,∠ACB=∠ECD,
∴△ABC≌△EDC,
∴AB=ED.
11. 如图,在△ABC中,∠A = 120°,AB = AC,D是BC边的中点,DE⊥AB,DF⊥AC,点E、F为垂足. 求证:△DEF是等边三角形.
证明:连接AD,
∵AB=AC,D是BC中点,
∴AD平分∠BAC,
又∵DE⊥AB,DF⊥AC,
∴DE=DF.
11. 如图,在△ABC中,∠A = 120°,AB = AC,D是BC边的中点,DE⊥AB,DF⊥AC,点E、F为垂足. 求证:△DEF是等边三角形.
∵∠A=120°,AB=AC,
∴∠B=∠C=30°,
∴∠BDE=∠CDF=60°,
∴∠EDF=180°-(∠BDE+∠CDF)=60°
∴ △DEF是等边三角形.
12. 如图,在△ABC中,∠C = 90°,∠A = 36°,DE是线段AB的垂直平分线,交AB于点D,交AC于点E. 求证:∠EBC=18°.
证明:∵∠C=90°,∠A=36°,
∴∠ABC=54°.
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠A=∠EBA=36°,
∴∠EBC=∠ABC-∠EBA=18°.
A
B
C
D
E
13. 如图,AB = AD,AC = AE,∠BAE = ∠DAC. 求证:∠C = ∠E.
证明:∵∠BAE=∠DAC,
∴∠BAE+∠EAC=∠DAC+∠EAC,
即∠BAC=∠DAE.
在△BAC和△DAE 中,
∵AB =AD,∠BAC=∠DAE,AC=AE,
∴△BAC≌△DAE,
∴∠C=∠E.
A
B
C
D
E
14. 如图,BF⊥AC,CE⊥AB,BE = CF,BF与CE交于点D. 求证:AD平分∠BAC.
证明:∵BF⊥AC,CE⊥AB,
∴∠ BED=∠CFD=90°.
在△BED和△CFD中,
∵∠BED=∠CFD,∠EDB=∠FDC,BE=CF,
∴△BED≌△CFD,
∴DE=DF.
又∵BF⊥AC,CE⊥AB,
∴AD 平分∠BAC.
15. 如图,AD=BC,∠ADC = ∠BCD. 求证:∠BAC = ∠ABD.
证明:∵在△ADC和△BCD中,
∵AD=BC,∠ADC=∠BCD,DC=CD,
∴△ADC≌△BCD,.
∴AC=BD.
在△ABD和△BAC中,
∵AD=BC,AB= BA,AC=BD,
∴△ABD≌△BAC,
∴∠BAC=∠ABD.
16. 如图,已知△ABC,求作点P,使AP=CP,且点P到边BA、BC的距离相等.
提示:作 AC的垂直平分线和∠ABC的平分线,交点即为点P.
17.两个直角三角形有两个角及一条边分别相等,这两个直角三角形会全等吗?试列出各种情况,并一一加以说明.
不一定.①当直角和一锐角相等,一条边是斜边或锐角的对边或两角的夹边对应相等,这两个三角形全等. ②当直角和一锐角相等,一个三角形的斜边和另一个三角形的直角边相等或一个三角形的锐角的邻边和另一个三角形锐角的对边相等,它们不全等.
18.如图,已知Rt△ABC≌Rt△ADE,∠ABC = ∠ADE = 90°, BC与DE相交于点F,连结CD、EB.
(1)请找出图中其他的全等三角形;
(2)试证明CF = EF.
(1)△ADC≌△ABE;
△CDF≌△EBF ;
(2)证明:连结CE.
∵Rt△ABC≌Rt△ADE,
∴AC=AE,∠ACB=∠AED,
∴∠ACE=∠AEC,
∠ACE-∠ACB=∠AEC-∠AED,
即∠BCE=∠DEC,
∴CF=EF
19.如图,在△ABC 与△ABD中,AD与BC相交于点O,∠1 = ∠2,请你添加一个条件(不再添加其他线段,不再标注或使用其他字母),使AC = BD,并给出证明.
你添加的条件是:_________________.
∠C=∠D
证明:∵∠1=∠2,
∴OA =OB.
在△AOC和△BOD 中,
∵∠C=∠D, ∠COA=∠DOB,OA=OB
∴△AOC≌△BOD,∴AC=BD.
