华师版八上数学第12章 整式的乘除 章末复习课件 (共35张PPT)
文档属性
| 名称 | 华师版八上数学第12章 整式的乘除 章末复习课件 (共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-01 17:40:22 | ||
图片预览







文档简介
(共35张PPT)
章末复习
华东师大版 八年级数学上册
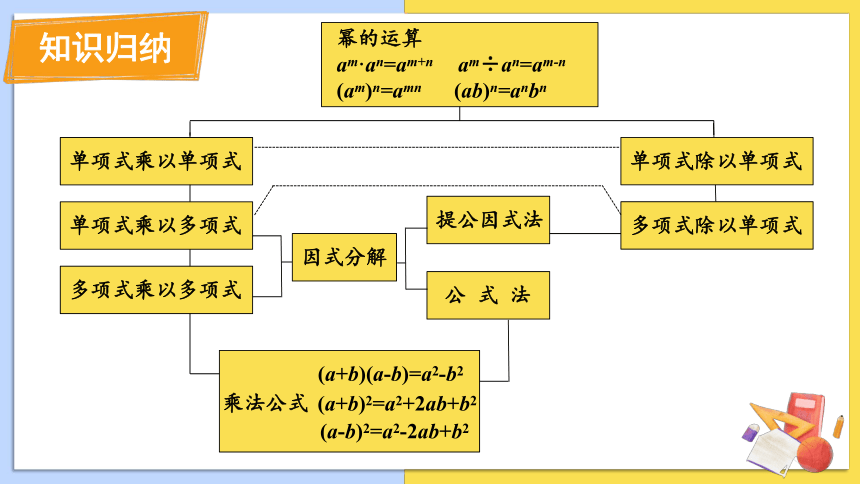
知识归纳
单项式乘以单项式
单项式乘以多项式
多项式乘以多项式
单项式除以单项式
多项式除以单项式
乘法公式
(a+b)(a-b)=a2-b2
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
幂的运算
am·an=am+n am÷an=am-n
(am)n=amn (ab)n=anbn
因式分解
提公因式法
公 式 法
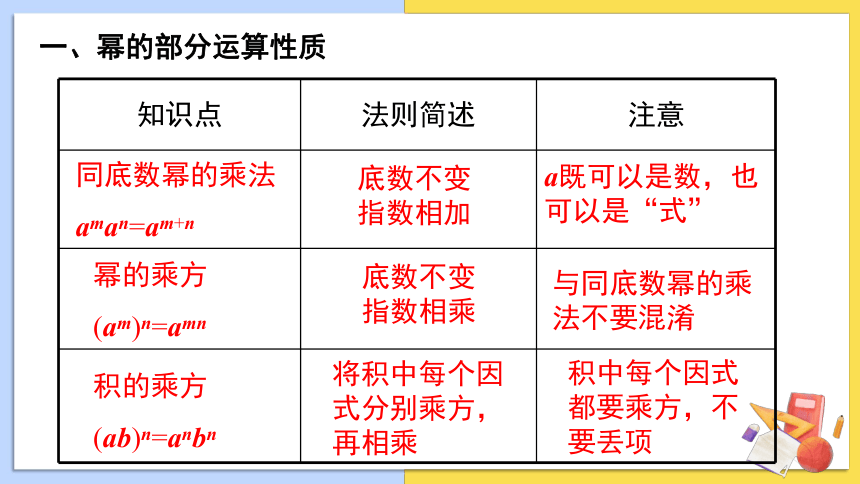
知识点 法则简述 注意
同底数幂的乘法
aman=am+n
幂的乘方
(am)n=amn
积的乘方
(ab)n=anbn
底数不变指数相加
a既可以是数,也可以是“式”
底数不变指数相乘
与同底数幂的乘法不要混淆
将积中每个因式分别乘方,再相乘
积中每个因式都要乘方,不要丢项
一、幂的部分运算性质
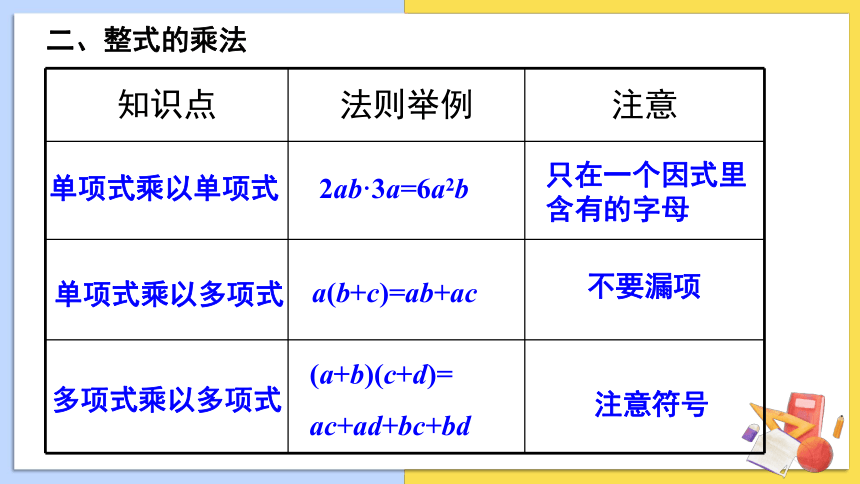
知识点 法则举例 注意
单项式乘以单项式
单项式乘以多项式
多项式乘以多项式
2ab·3a=6a2b
只在一个因式里含有的字母
a(b+c)=ab+ac
不要漏项
(a+b)(c+d)=
ac+ad+bc+bd
注意符号
二、整式的乘法
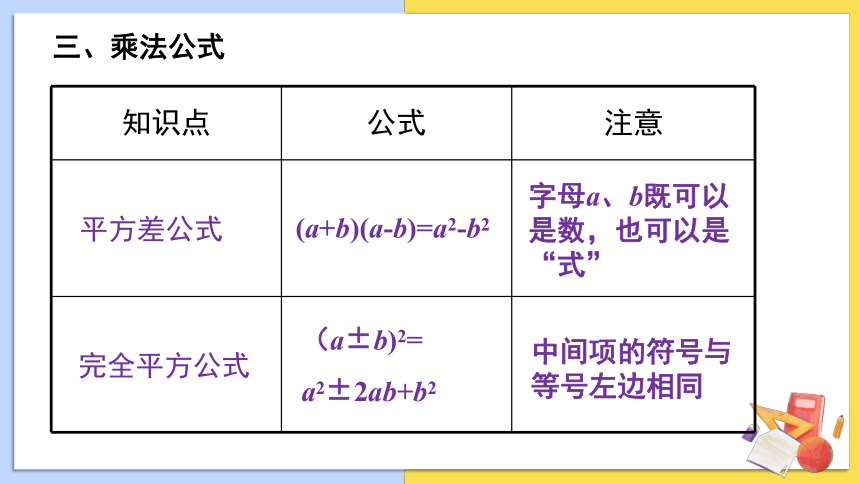
知识点 公式 注意
三、乘法公式
平方差公式
完全平方公式
(a+b)(a-b)=a2-b2
(a±b)2=
a2±2ab+b2
字母a、b既可以是数,也可以是“式”
中间项的符号与等号左边相同
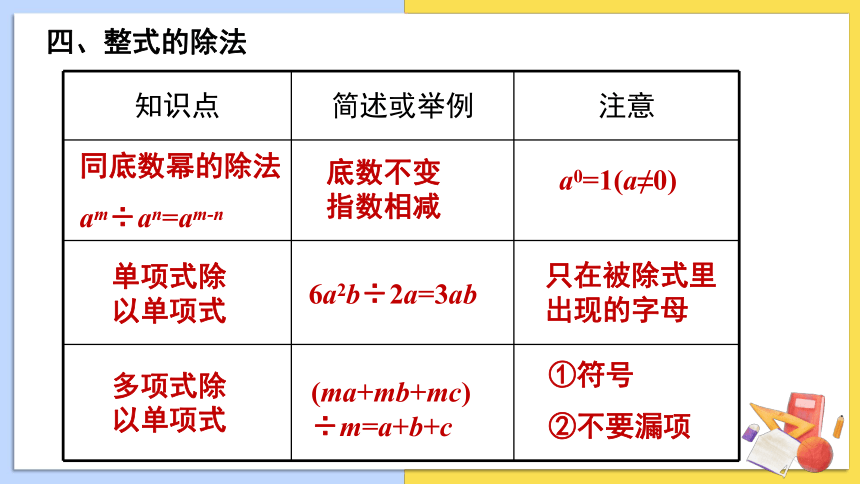
知识点 简述或举例 注意
同底数幂的除法
am÷an=am-n
单项式除以单项式
多项式除以单项式
底数不变指数相减
a0=1(a≠0)
6a2b÷2a=3ab
只在被除式里出现的字母
(ma+mb+mc) ÷m=a+b+c
①符号
②不要漏项
四、整式的除法
随堂练习
1.计算:
(1)a10·a8
(2)(xy)2·(xy)3
(3)[(-x)3]2
(4)[(-x)2]3
(5)(-2mn2)3
(6)(y3)2·(y2)4
=a10+8=a18
=(xy)2+3=(xy)5=x5y5
=(-x)6=x6
=(-x)6=x6
=-8m3n6
=y6·y8=y14
A组
2.计算:
(1)2a·3a2
(2)(-3xy)·(-4yz)
(3)(-2a2)2·(-5a3)
(4)(-3x)·(2x2-x-1)
=2·3a·a2
=6a3
=(-3)×(-4)xy·yz
=12xy2z
=4a4·(-5a3)
=4×(-5)a4·a3
=-20a7
=(-3x)·2x2-(-3x)x-(-3x)
=-6x3+3x2+3x
2.计算:
(5)(x-2)(x-6)
(6)(2x-1)(3x+2)
(7)(y-2)(y2-6y-9)
(8)(p-6q)(p2+pq+q2)
=(x-2)x-6(x-2)
=x2-2x-6x+12
=x2-8x+12
=2x(3x+2)-(3x+2)
=6x2+4x-3x-2
=6x2+x-2
=y(y2-6y-9)-2(y2-6y-9)
=y3-6y2-9y-2y2+12y+18
=y3-8y2+3y+18
=p(p2+pq+q2)-6q(p2+pq+q2)
=p3+p2q+pq2-6p2q-6pq2-6q3
=p3-5p2q-5pq2-6q3
3.计算:
(1)(x+2)(x-2)
(2)(m+n)(m-n)
(3)(-m-n)(-m+n)
(4)(-m-n)(m+n)
=x2-4
=m2-n2
=-(m+n)(n-m)
=-(n2-m2)
=-n2+m2
=-(m+n)(m+n)
=-(m2+2mn+n2)
=-m2-2mn-n2
(5)(-m+n)(m-n)
=-(m-n)(m-n)
=-(m2-2mn+n2)
=-m2+2mn-n2
4.计算:
(1)20132-2014×2012
(2)(4×104)×(2×103)-(6.5×103)×(6×103)
=20132-(2013+1)×(2013-1)
=20132-20132+1=1
=8×104×103-39×103×103
=8×107-3.9×107
=4.1×107
4.计算:
(3)(2x+5)2-(2x-5)2
(4)
=(2x+5-2x+5)(2x+5+2x-5)
=10·4x
=40x
= -4x
4.计算:
(5)(-2x2) ·(-y)+3xy·(1- x)
(6)(-6x2)2+(-3x)3·x
=2x2y+3xy-x2y
=3xy+x2y
=36x4-27x3·x
=9x4
5.计算:
(1)a·a4÷a3
(2)(-x)6÷(-x)2·(-x)3
(3)27x8÷3x4
(4)-12m3n3÷4m2n3
=a5÷a3
=a2
= (-x)6-2+3
=-x7
=9x8-4
=9x4
=-3m3-2n3-3
=-3m
5.计算:
(5)(6x2y3z2)2÷4x3y4
(6)(-6a2b5c)÷(-2ab2)2
=36x4y6z4÷4x3y4
=9x4-3y6-4z4
=9xy2z4
=(-6a2b5c)÷4a2b4
=-1.5a2-2b5-4c
=-1.5bc
6.计算:
(1)(6a4-4a3-2a2)÷(-2a2)
(2)(4x3y+6x2y2-xy3)÷2xy
=6a4÷(-2a2)-4a3÷(-2a2)-2a2÷(-2a2)
=-3a2+2a+1
=4x3y÷2xy+6x2y2÷2xy-xy3÷2xy
=2x2+3xy-0.5y2
6.计算:
(3)(x4+2x3- x2)÷(- x)2
(4)(2ab2-b3)2÷2b3
=x4 +2x3 - x2
÷(- x)2
÷(- x)2
÷(- x)2
=4x2+8x-2
=(4a2b4-4ab5+b6)÷2b3
=4a2b4÷2b3-4ab5÷2b3+b6÷2b3
=2a2b-2ab2+0.5b3
7.计算:[(x-2y)2+(x-2y)(x+2y)-2x(2x-y)]÷2x.
解: [(x-2y)[(x-2y)+(x+2y)]-2x(2x-y)]÷2x.
=[2x(x-2y)-2x(2x-y)]÷2x.
=2x(x-2y-2x+y)÷2x.
=-x-y
8.把下列多项式分解因式:
(1)x2-25x
(2)2x2y2-4y3z
(3)am-an+ap
(4)x3-25x
=x(x-25)
=2y2(x2-2yz)
=a(m-n+p)
=x(x2-25)
=x(x+5)(x-5)
8.把下列多项式分解因式:
(5)1-4x2
(6)25x2+20xy+4y2
(7)x3-4x2+4x
=(1-2x)(1+2x)
=(5x+2y)2
=x(x2-4x+4)
=x(x-2)2
9.先化简,再求值:
(1)3a(2a2-4a+3)-2a2(3a+4),其中a=-2;
解: 3a(2a2-4a+3)-2a2(3a+4)
=6a3-12a2+9a-6a3-8a2
=-20a2+9a
当a=-2时,原式=-20×(-2)2+9×(-2)=-80-18=-98
(2)(a-3b)2+(3a+b)2-(a+5b)2+(a-5b)2,其中a=-8,b=-6;
解 (a-3b)2+(3a+b)2-(a+5b)2+(a-5b)2
=(a2-6ab+9b2)+(9a2+6ab+b2) –
(a2 +10ab+25b2) +(a2-10ab+25b2)
=a2-6ab+9b2 +9a2+6ab+b2 –
a2 -10ab-25b2+a2-10ab+25b2
=10a2+10b2-20ab
=10(a-b)2
当a=-8,b=-6时,原式=10×(-8+6)2=40.
10.求下列各式的值:
(1)(3x4-2x3)÷(-x)-(x-x2)·3x,其中x= .
解:(3x4-2x3)÷(-x)-(x-x2)·3x
=-3x3+2x2-(3x2-3x3)
=-3x3+2x2-3x2+3x3
=-x2
当x= 时,原式=-( )2= .
B组
10.求下列各式的值:
(2)[(ab+1)(ab-2)-2a2b2+2]÷(-ab),其中a= ,b= ;
解: [(ab+1)(ab-2)-2a2b2+2]÷(-ab)
=[(ab+1)(ab-2)-2(a2b2-1)]÷(-ab)
=ab+1
当a= ,b= 时,原式= =-1
=[(ab+1)(ab-2)-2(ab+1)(ab-1)]÷(-ab)
=[(ab+1)[(ab-2)-2(ab-1)]]÷(-ab)
=(ab+1)(-ab)÷(-ab)
11.已知(x+y)2=1, (x-y)2=49,求x2+y2 与xy的值.
解: ∵ (x+y)2=1
∴x2+2xy+y2=1
∵ (x-y)2=49
∴x2-2xy+y2=49
∴解得x2+y2=25,xy=-12
12.已知a+b=3, ab=2,求a2+b2 的值.
解: a2+b2=a2+b2+2ab-2ab
=(a+b)2-2ab
=32-2×2
=5
13.已知a-b=1, a2+b2=25,求ab的值.
解: ab=[-(a-b)2+a2+b2]÷2
=(-12+25)÷2
=12
14.把下列多项式分解因式:
(1)x(x+y)-y(x+y)
(2)(a+b)2+2(a+b)+1
(3)4x4+4x3+x2
(4)x2-16ax+64a2
=(x-y)(x+y)
=(a+b+1)2
=x2(4x2+4x+1)
=x2(2x+1)2
=(x2-8a)2
14.把下列多项式分解因式:
(5)(x-1)(x-3)+1
(6)(ab+a)+(b+1)
=(x2-4x+3)+1
=x2-4x+4
=(x-2)2
=a(b+1)+(b+1)
=(a+1)(b+1)
15.(1)一个正方形的边长增加3cm,它的面积增加了45cm2,求原来这个正方形的边长.
(2)一个正方形的边长减少3cm,它的面积减少了45cm2,原来这个正方形的边长是多少呢?它和题(1)的答案相同吗?
解:(1)设原边长为xcm,则(x+3)2-x2=45
解得 x=6(cm)
(2)设原边长为xcm,则x2-(x-3)2=45
解得 x=9(cm)
答案不相同
16.已知一个长方形,若它的长增加4cm,宽减少1cm,则面积保持不变;若它的长减少2cm,宽增加1cm,则面积仍保持不变.求这个长方形的面积.
解:设这个长方形的长与宽分别为acm和bcm
依题意,得
(a+4)(b-1)=ab
(a-2)(b+1)=ab
解得
a=8
b=3
即长方形的面积为ab=8×3=24(cm2)
C组
17.已知M是含字母x的单项式,要使多项式4x2+M+1是某一个多项式的平方,求M.
解:当M=±4x时或M=4x4时,4x2+M+1是一个多项式的平方.
18.判断下列说法是否正确,并说明理由:
(1)两个连续整数的平方差必是奇数;
解:(1)正确.设两个连续的数分别为x,x+1,则它们的平方差表示为(x+1)2-x2=2x+1.
而当x为整数时,2x+1总是一个奇数.
18.判断下列说法是否正确,并说明理由:
(2)若a为整数,则a3-a能被6整除.
解:(2)正确.因为a3-a=a(a+1)(a-1)
当a为整数时,a-1,a,a+1恰好为三个连续的整数,而任何三个连续整数中,必有一个能被3整除,且至少有一个偶数,能被2整除,故三个连续整数的乘积必能被6整除,即a3-a能被6整除.
章末复习
华东师大版 八年级数学上册
知识归纳
单项式乘以单项式
单项式乘以多项式
多项式乘以多项式
单项式除以单项式
多项式除以单项式
乘法公式
(a+b)(a-b)=a2-b2
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
幂的运算
am·an=am+n am÷an=am-n
(am)n=amn (ab)n=anbn
因式分解
提公因式法
公 式 法
知识点 法则简述 注意
同底数幂的乘法
aman=am+n
幂的乘方
(am)n=amn
积的乘方
(ab)n=anbn
底数不变指数相加
a既可以是数,也可以是“式”
底数不变指数相乘
与同底数幂的乘法不要混淆
将积中每个因式分别乘方,再相乘
积中每个因式都要乘方,不要丢项
一、幂的部分运算性质
知识点 法则举例 注意
单项式乘以单项式
单项式乘以多项式
多项式乘以多项式
2ab·3a=6a2b
只在一个因式里含有的字母
a(b+c)=ab+ac
不要漏项
(a+b)(c+d)=
ac+ad+bc+bd
注意符号
二、整式的乘法
知识点 公式 注意
三、乘法公式
平方差公式
完全平方公式
(a+b)(a-b)=a2-b2
(a±b)2=
a2±2ab+b2
字母a、b既可以是数,也可以是“式”
中间项的符号与等号左边相同
知识点 简述或举例 注意
同底数幂的除法
am÷an=am-n
单项式除以单项式
多项式除以单项式
底数不变指数相减
a0=1(a≠0)
6a2b÷2a=3ab
只在被除式里出现的字母
(ma+mb+mc) ÷m=a+b+c
①符号
②不要漏项
四、整式的除法
随堂练习
1.计算:
(1)a10·a8
(2)(xy)2·(xy)3
(3)[(-x)3]2
(4)[(-x)2]3
(5)(-2mn2)3
(6)(y3)2·(y2)4
=a10+8=a18
=(xy)2+3=(xy)5=x5y5
=(-x)6=x6
=(-x)6=x6
=-8m3n6
=y6·y8=y14
A组
2.计算:
(1)2a·3a2
(2)(-3xy)·(-4yz)
(3)(-2a2)2·(-5a3)
(4)(-3x)·(2x2-x-1)
=2·3a·a2
=6a3
=(-3)×(-4)xy·yz
=12xy2z
=4a4·(-5a3)
=4×(-5)a4·a3
=-20a7
=(-3x)·2x2-(-3x)x-(-3x)
=-6x3+3x2+3x
2.计算:
(5)(x-2)(x-6)
(6)(2x-1)(3x+2)
(7)(y-2)(y2-6y-9)
(8)(p-6q)(p2+pq+q2)
=(x-2)x-6(x-2)
=x2-2x-6x+12
=x2-8x+12
=2x(3x+2)-(3x+2)
=6x2+4x-3x-2
=6x2+x-2
=y(y2-6y-9)-2(y2-6y-9)
=y3-6y2-9y-2y2+12y+18
=y3-8y2+3y+18
=p(p2+pq+q2)-6q(p2+pq+q2)
=p3+p2q+pq2-6p2q-6pq2-6q3
=p3-5p2q-5pq2-6q3
3.计算:
(1)(x+2)(x-2)
(2)(m+n)(m-n)
(3)(-m-n)(-m+n)
(4)(-m-n)(m+n)
=x2-4
=m2-n2
=-(m+n)(n-m)
=-(n2-m2)
=-n2+m2
=-(m+n)(m+n)
=-(m2+2mn+n2)
=-m2-2mn-n2
(5)(-m+n)(m-n)
=-(m-n)(m-n)
=-(m2-2mn+n2)
=-m2+2mn-n2
4.计算:
(1)20132-2014×2012
(2)(4×104)×(2×103)-(6.5×103)×(6×103)
=20132-(2013+1)×(2013-1)
=20132-20132+1=1
=8×104×103-39×103×103
=8×107-3.9×107
=4.1×107
4.计算:
(3)(2x+5)2-(2x-5)2
(4)
=(2x+5-2x+5)(2x+5+2x-5)
=10·4x
=40x
= -4x
4.计算:
(5)(-2x2) ·(-y)+3xy·(1- x)
(6)(-6x2)2+(-3x)3·x
=2x2y+3xy-x2y
=3xy+x2y
=36x4-27x3·x
=9x4
5.计算:
(1)a·a4÷a3
(2)(-x)6÷(-x)2·(-x)3
(3)27x8÷3x4
(4)-12m3n3÷4m2n3
=a5÷a3
=a2
= (-x)6-2+3
=-x7
=9x8-4
=9x4
=-3m3-2n3-3
=-3m
5.计算:
(5)(6x2y3z2)2÷4x3y4
(6)(-6a2b5c)÷(-2ab2)2
=36x4y6z4÷4x3y4
=9x4-3y6-4z4
=9xy2z4
=(-6a2b5c)÷4a2b4
=-1.5a2-2b5-4c
=-1.5bc
6.计算:
(1)(6a4-4a3-2a2)÷(-2a2)
(2)(4x3y+6x2y2-xy3)÷2xy
=6a4÷(-2a2)-4a3÷(-2a2)-2a2÷(-2a2)
=-3a2+2a+1
=4x3y÷2xy+6x2y2÷2xy-xy3÷2xy
=2x2+3xy-0.5y2
6.计算:
(3)(x4+2x3- x2)÷(- x)2
(4)(2ab2-b3)2÷2b3
=x4 +2x3 - x2
÷(- x)2
÷(- x)2
÷(- x)2
=4x2+8x-2
=(4a2b4-4ab5+b6)÷2b3
=4a2b4÷2b3-4ab5÷2b3+b6÷2b3
=2a2b-2ab2+0.5b3
7.计算:[(x-2y)2+(x-2y)(x+2y)-2x(2x-y)]÷2x.
解: [(x-2y)[(x-2y)+(x+2y)]-2x(2x-y)]÷2x.
=[2x(x-2y)-2x(2x-y)]÷2x.
=2x(x-2y-2x+y)÷2x.
=-x-y
8.把下列多项式分解因式:
(1)x2-25x
(2)2x2y2-4y3z
(3)am-an+ap
(4)x3-25x
=x(x-25)
=2y2(x2-2yz)
=a(m-n+p)
=x(x2-25)
=x(x+5)(x-5)
8.把下列多项式分解因式:
(5)1-4x2
(6)25x2+20xy+4y2
(7)x3-4x2+4x
=(1-2x)(1+2x)
=(5x+2y)2
=x(x2-4x+4)
=x(x-2)2
9.先化简,再求值:
(1)3a(2a2-4a+3)-2a2(3a+4),其中a=-2;
解: 3a(2a2-4a+3)-2a2(3a+4)
=6a3-12a2+9a-6a3-8a2
=-20a2+9a
当a=-2时,原式=-20×(-2)2+9×(-2)=-80-18=-98
(2)(a-3b)2+(3a+b)2-(a+5b)2+(a-5b)2,其中a=-8,b=-6;
解 (a-3b)2+(3a+b)2-(a+5b)2+(a-5b)2
=(a2-6ab+9b2)+(9a2+6ab+b2) –
(a2 +10ab+25b2) +(a2-10ab+25b2)
=a2-6ab+9b2 +9a2+6ab+b2 –
a2 -10ab-25b2+a2-10ab+25b2
=10a2+10b2-20ab
=10(a-b)2
当a=-8,b=-6时,原式=10×(-8+6)2=40.
10.求下列各式的值:
(1)(3x4-2x3)÷(-x)-(x-x2)·3x,其中x= .
解:(3x4-2x3)÷(-x)-(x-x2)·3x
=-3x3+2x2-(3x2-3x3)
=-3x3+2x2-3x2+3x3
=-x2
当x= 时,原式=-( )2= .
B组
10.求下列各式的值:
(2)[(ab+1)(ab-2)-2a2b2+2]÷(-ab),其中a= ,b= ;
解: [(ab+1)(ab-2)-2a2b2+2]÷(-ab)
=[(ab+1)(ab-2)-2(a2b2-1)]÷(-ab)
=ab+1
当a= ,b= 时,原式= =-1
=[(ab+1)(ab-2)-2(ab+1)(ab-1)]÷(-ab)
=[(ab+1)[(ab-2)-2(ab-1)]]÷(-ab)
=(ab+1)(-ab)÷(-ab)
11.已知(x+y)2=1, (x-y)2=49,求x2+y2 与xy的值.
解: ∵ (x+y)2=1
∴x2+2xy+y2=1
∵ (x-y)2=49
∴x2-2xy+y2=49
∴解得x2+y2=25,xy=-12
12.已知a+b=3, ab=2,求a2+b2 的值.
解: a2+b2=a2+b2+2ab-2ab
=(a+b)2-2ab
=32-2×2
=5
13.已知a-b=1, a2+b2=25,求ab的值.
解: ab=[-(a-b)2+a2+b2]÷2
=(-12+25)÷2
=12
14.把下列多项式分解因式:
(1)x(x+y)-y(x+y)
(2)(a+b)2+2(a+b)+1
(3)4x4+4x3+x2
(4)x2-16ax+64a2
=(x-y)(x+y)
=(a+b+1)2
=x2(4x2+4x+1)
=x2(2x+1)2
=(x2-8a)2
14.把下列多项式分解因式:
(5)(x-1)(x-3)+1
(6)(ab+a)+(b+1)
=(x2-4x+3)+1
=x2-4x+4
=(x-2)2
=a(b+1)+(b+1)
=(a+1)(b+1)
15.(1)一个正方形的边长增加3cm,它的面积增加了45cm2,求原来这个正方形的边长.
(2)一个正方形的边长减少3cm,它的面积减少了45cm2,原来这个正方形的边长是多少呢?它和题(1)的答案相同吗?
解:(1)设原边长为xcm,则(x+3)2-x2=45
解得 x=6(cm)
(2)设原边长为xcm,则x2-(x-3)2=45
解得 x=9(cm)
答案不相同
16.已知一个长方形,若它的长增加4cm,宽减少1cm,则面积保持不变;若它的长减少2cm,宽增加1cm,则面积仍保持不变.求这个长方形的面积.
解:设这个长方形的长与宽分别为acm和bcm
依题意,得
(a+4)(b-1)=ab
(a-2)(b+1)=ab
解得
a=8
b=3
即长方形的面积为ab=8×3=24(cm2)
C组
17.已知M是含字母x的单项式,要使多项式4x2+M+1是某一个多项式的平方,求M.
解:当M=±4x时或M=4x4时,4x2+M+1是一个多项式的平方.
18.判断下列说法是否正确,并说明理由:
(1)两个连续整数的平方差必是奇数;
解:(1)正确.设两个连续的数分别为x,x+1,则它们的平方差表示为(x+1)2-x2=2x+1.
而当x为整数时,2x+1总是一个奇数.
18.判断下列说法是否正确,并说明理由:
(2)若a为整数,则a3-a能被6整除.
解:(2)正确.因为a3-a=a(a+1)(a-1)
当a为整数时,a-1,a,a+1恰好为三个连续的整数,而任何三个连续整数中,必有一个能被3整除,且至少有一个偶数,能被2整除,故三个连续整数的乘积必能被6整除,即a3-a能被6整除.
