【高中数学北师大版必修第一册同步练习】 5.2.实际问题中的函数模型(含答案)
文档属性
| 名称 | 【高中数学北师大版必修第一册同步练习】 5.2.实际问题中的函数模型(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 20:31:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【高中数学北师大版必修第一册同步练习】
5.2.实际问题中的函数模型
一、单选题
1.如果在2020年以后,每年的GDP(国民生产总值)比上一年平均增加8%,那么到哪年GDP基本实现翻两番的目标?(参考数据: , )( )
A.2032 B.2035 C.2038 D.2041
2.《九章算术》是我国古代的数学巨著,书中有这样一道题:“今有垣厚五尺,两鼠对穿.大鼠日一尺,小鼠亦日一尺,大鼠日自倍,小鼠日自半.问何日相逢?”题意为:有一堵墙厚五尺,有两只老鼠从墙的正对面打洞穿墙.大老鼠第一天打进一尺,以后每天打进的长度是前一天的2倍;小老鼠第一天也打进一尺,以后每天打进的长度是前一天的一半.若这一堵墙厚 尺,则几日后两鼠相逢( )
A.3 B.4 C.5 D.6
3.Logistic模型是常用数学模型之一,可应用于流行病学领域有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数 (t的单位:天)的Logistic模型: ,其中K为最大确诊病例数.当 时,标志着已初步遏制疫情,则 约为( )(已知 )
A.60 B.63 C.66 D.69
4.在流行病学中,基本传染数是指每名感染者平均可传染的人数.当基本传染数高于1时,每个感染者平均会感染一个以上的人,从而导致感染这种疾病的人数量指数级增长.当基本传染数持续低于1时,疫情才可能逐渐消散.广泛接种疫苗可以减少疾病的基本传染数.假设某种传染病的基本传染数为 ,1个感染者在每个传染期会接触到 个新人,这 人中有 个人接种过疫苗( 称为接种率),那么1个感染者新的传染人数为 .已知新冠病毒在某地的基本传染数 为了使1个感染者传染人数不超过1,该地疫苗的接种率至少为( )
A.40% B.50% C.60% D.70%
5.如图,直线 与单位圆相切于点 ,射线 从 出发,绕着点 逆时针旋转,在旋转的过程中,记 ( ), 所经过的单位圆 内区域(阴影部分)的面积为 ,记 ,则下列选项判断正确的是( )
A.当 时,
B.对任意 ,且 ,都有
C.对任意 ,都有
D.对任意 ,都有
6.某商店将进价为40元的商品按50元一件销售,一个月恰好卖500件,而价格每提高1元,就会少卖10个,商店为使该商品利润最大,应将每件商品定价为( )
A.50元 B.60元 C.70元 D.100元
二、多选题
7.据美国学者詹姆斯·马丁的测算,近十年,人类知识总量已达到每三年翻一番,到2020年甚至要达到每73天翻一番的空前速度.因此,基础教育的任务已不是教会一切人一切知识,而是让一切人学会学习.已知2000年底,人类知识总量为a ,假如从2000年底到2009年底是每三年翻一番,从2009年底到2019年底是每一年翻一番,2020年(按365天计算)是每73天翻一番,则下列说法正确的是( )
A.2006年底人类知识总量是2a B.2009年底人类知识总量是8a
C.2019年底人类知识总量是213a D.2020年底人类知识总量是218a
三、填空题
8.某食品的保鲜时间y(单位:小时)与储存温度x(单位: )满足函数关系 ( 为自然对数的底数,k、b为常数)。若该食品在0 的保鲜时间设计192小时,在22 的保鲜时间是48小时,则该食品在33 的保鲜时间是 小时.
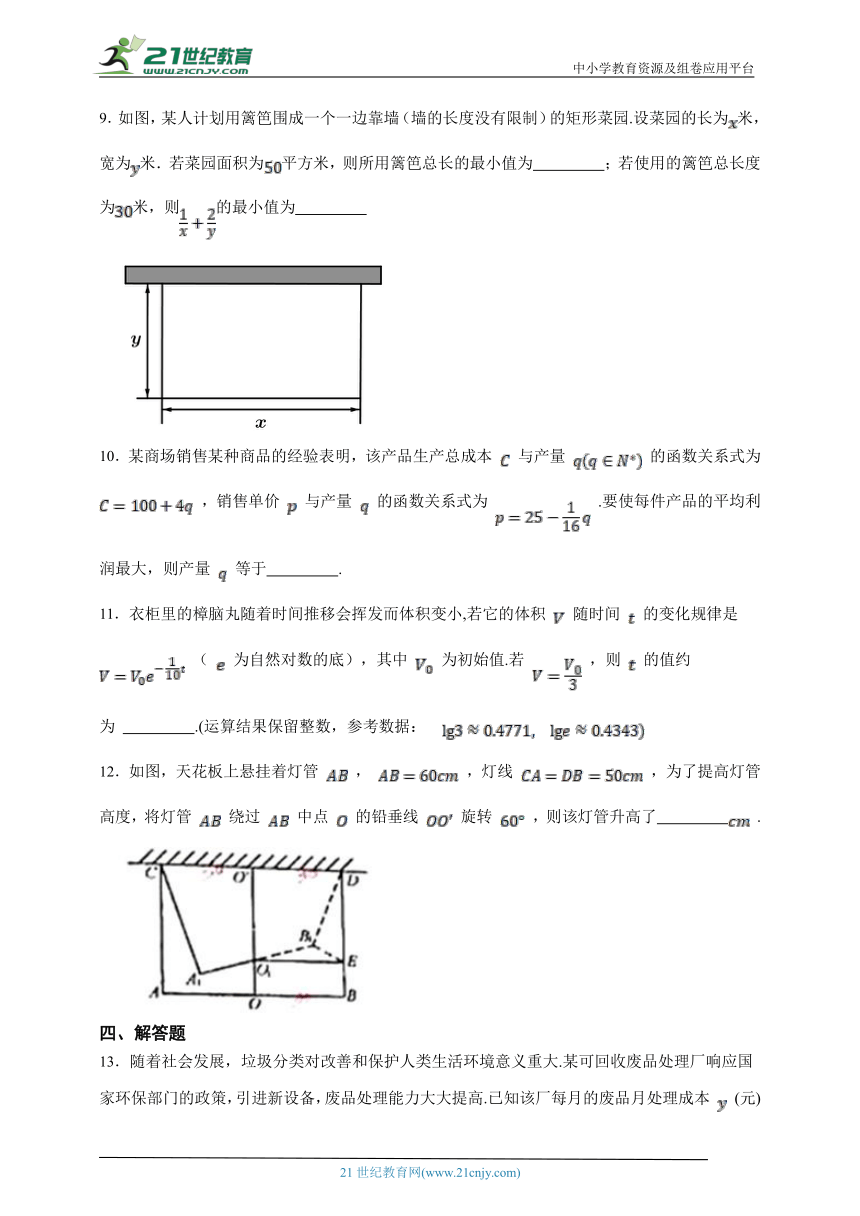
9.如图,某人计划用篱笆围成一个一边靠墙(墙的长度没有限制)的矩形菜园.设菜园的长为米,宽为米.若菜园面积为平方米,则所用篱笆总长的最小值为 ;若使用的篱笆总长度为米,则的最小值为
10.某商场销售某种商品的经验表明,该产品生产总成本 与产量 的函数关系式为 ,销售单价 与产量 的函数关系式为 .要使每件产品的平均利润最大,则产量 等于 .
11.衣柜里的樟脑丸随着时间推移会挥发而体积变小,若它的体积 随时间 的变化规律是 ( 为自然对数的底),其中 为初始值.若 ,则 的值约为 .(运算结果保留整数,参考数据:
12.如图,天花板上悬挂着灯管 , ,灯线 ,为了提高灯管高度,将灯管 绕过 中点 的铅垂线 旋转 ,则该灯管升高了 .
四、解答题
13.随着社会发展,垃圾分类对改善和保护人类生活环境意义重大.某可回收废品处理厂响应国家环保部门的政策,引进新设备,废品处理能力大大提高.已知该厂每月的废品月处理成本 (元)与月处理量 (千吨)之间近似地的构成二次函数关系,经调研发现,该厂每月处理量 最少100千吨,最多500千吨.当月处理量为200千吨时,月处理成本最低,为50000元,且在月处理量最少的情况下,耗费月处理成本60000元.
(1)求月处理成本 (元)与月处理量 (千吨)之间函数关系式;
(2)该厂每月废品处理量为多少千吨时,才能使每千吨的处理成本最低?
(3)若该厂每处理一千吨废品获利400元,则每月能否获利?若获利,求出最大利润.
14.一批救灾物资随51辆汽车从某市以 的速度匀速直达灾区.已知两地公路线长 ,为了安全起见,两辆汽车的间距不得小于 ,那么这批物资全部到达灾区最少需要多长时间?
15.生命在于运动,运动在于锻炼.其中,游泳就是一个非常好的锻炼方式.游泳有众多好处:强.身健体;保障生命安全;增强心肺功能;锻炼意志,培养勇敢顽强精神;休闲娱乐,促进身心健康.近几年,游泳池成了新小区建设的标配.家门口的“游泳池”,成了市民休闲娱乐的好去处.如图,某小区规划一个深度为,底面积为的矩形游泳池,按规划要求:在游泳池的四周安排宽的休闲区,休闲区造价为元,游泳池的底面与墙面铺设瓷砖,瓷砖造价为元.其他设施等支出大约为万元,设游泳池的长为.
(1)试将总造价(元)表示为长度的函数;
(2)当取何值时,总造价最低,并求出最低总造价.
16.某公司今年一月份推出新产品A,其成本价为492元/件,经试销调查,销售量与销售价的关系如下表:
销售价(x/元件) 650 662 720 800
销售量(y件) 350 333 281 200
由此可知,销售量y(件)与销售价x(元/件)可近似看作一次函数y=kx+b的关系(通常取表中相距较远的两组数据所得一次函数较为精确).
(1)写出以x为自变量的函数y的解析式及定义域;
(2)试问:销售价定为多少时,一月份销售利润最大?并求最大销售利润和此时的销售量.
17.榆林市政府坚持保护环境和节约资源,坚持推进生态文明建设。若市财政局下拨专款100百万元,分别用于植绿护绿和处理污染两个生态维护项目,植绿护绿项目五年内带来的生态收益可表示为投放资金 (单位:百万元)的函数 (单位:百万元): ,处理污染项目五年内带来的生态收益可表示为投放资金 单位:(单位:百万元)的函数 (单位:百万元): 。
(1)设分配给植绿护绿项目的资金为 (百万元),则两个生态项目五年内带来的收益总和为y,写出y关于 的函数解析式和定义域;
(2)试求出y的最大值,并求出此时对两个生态项目的投资分别为多少?
18.如图,一载着重危病人的火车从地出发,沿北偏东射线行驶,其中,在距离地10公里北偏东角的处住有一位医学专家(其中),现有紧急征调离地正东公里的处的救护车赶往处载上医学专家全速追赶乘有重危病人的火车,并在处相遇,经计算当两车行驶的路线与围成的三角形面积最小时,抢救最及时.
(1)求关于的函数关系;
(2)当为何值时,抢救最及时.
答案解析部分
1.【答案】C
【知识点】根据实际问题选择函数类型
2.【答案】B
【知识点】根据实际问题选择函数类型
3.【答案】C
【知识点】函数模型的选择与应用
4.【答案】C
【知识点】函数模型的选择与应用
5.【答案】C
【知识点】函数模型的选择与应用
6.【答案】C
【知识点】函数模型的选择与应用
7.【答案】B,C,D
【知识点】函数模型的选择与应用
8.【答案】24
【知识点】函数模型的选择与应用
9.【答案】20;
【知识点】函数的最大(小)值;函数模型的选择与应用
10.【答案】40
【知识点】基本不等式在最值问题中的应用;函数模型的选择与应用
11.【答案】11
【知识点】函数模型的选择与应用
12.【答案】10
【知识点】函数模型的选择与应用
13.【答案】(1)解:由题意知:设该二次函数为 ,
当 时, ,
即 ,
解得: ,
,
故月处理成本 (元)与月处理量 (千吨)之间函数关系式为: ;
(2)由题意知每千吨的月处理成本:
,
当且仅当 时,即当 时, 有最小值200,
故该厂每月废品处理量为300千吨时,才能使每千吨的处理成本最低;
(3)设该厂每月利润 元,则由题意:
,
故当 时, 有最大值70000,即每月最大利润为70000元,
故能获利,最大利润为70000元.
【知识点】函数的最大(小)值;根据实际问题选择函数类型
14.【答案】当最后一辆车子出发时,第一辆车子走了 小时,
最后一辆车走完全程共需要 小时,
所以一共需要 小时,
由基本不等式 ,当且仅当 ,即 时等号成立,
故最少需要10小时.
【知识点】根据实际问题选择函数类型;基本不等式在最值问题中的应用
15.【答案】(1)解:因为游泳池的长为,所以游泳池的宽为,
铺游泳池的花费为,
休闲区的花费为,
所以,总造价为,其中;
(2)解:由基本不等式可得
(元),
当且仅当时,等号成立.
因此,当时,总造价最低,且最低总造价为元.
【知识点】根据实际问题选择函数类型;基本不等式
16.【答案】(1)解:由题意知 ,
解得k=﹣1,b=1000,∴y=﹣x+1000
由于y为非负整数,所以0≤x≤1000
(2)解:设一月份的利润为S元,由题意得S=(x﹣492)(1000﹣x)=﹣(x﹣746)2+64516
∴当x=746元/件时,一月份销售收入 最大为64516元
【知识点】函数模型的选择与应用
17.【答案】(1)解:由题意可得处理污染项目投放资金为 百万元,
所以 ,
∴ , ;
所以 ,
(2)解:由(1)得
当且仅当 ,即 时等号成立,
此时 .
∴y的最大值为52百万元,分别投资给植绿护绿项目、污染处理项目的资金为40百万元,60百万元.
【知识点】基本不等式在最值问题中的应用;函数模型的选择与应用
18.【答案】(1)解:建立如图所示的直角坐标系,
因为,所以,
因为,所以,
因为,所以射线的方程为,
因为,所以直线的斜率为(),
所以直线的方程为(),
当时,点,则,
当时,由,得(),
所以点(),
所以(),
综上,当时,,当且时,
(2)解:由(1)得当且时,
,
当且仅当,即时取等号,
而当时,,
所以当时,有最小值,即抢救最及时
【知识点】基本不等式在最值问题中的应用;函数模型的选择与应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【高中数学北师大版必修第一册同步练习】
5.2.实际问题中的函数模型
一、单选题
1.如果在2020年以后,每年的GDP(国民生产总值)比上一年平均增加8%,那么到哪年GDP基本实现翻两番的目标?(参考数据: , )( )
A.2032 B.2035 C.2038 D.2041
2.《九章算术》是我国古代的数学巨著,书中有这样一道题:“今有垣厚五尺,两鼠对穿.大鼠日一尺,小鼠亦日一尺,大鼠日自倍,小鼠日自半.问何日相逢?”题意为:有一堵墙厚五尺,有两只老鼠从墙的正对面打洞穿墙.大老鼠第一天打进一尺,以后每天打进的长度是前一天的2倍;小老鼠第一天也打进一尺,以后每天打进的长度是前一天的一半.若这一堵墙厚 尺,则几日后两鼠相逢( )
A.3 B.4 C.5 D.6
3.Logistic模型是常用数学模型之一,可应用于流行病学领域有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数 (t的单位:天)的Logistic模型: ,其中K为最大确诊病例数.当 时,标志着已初步遏制疫情,则 约为( )(已知 )
A.60 B.63 C.66 D.69
4.在流行病学中,基本传染数是指每名感染者平均可传染的人数.当基本传染数高于1时,每个感染者平均会感染一个以上的人,从而导致感染这种疾病的人数量指数级增长.当基本传染数持续低于1时,疫情才可能逐渐消散.广泛接种疫苗可以减少疾病的基本传染数.假设某种传染病的基本传染数为 ,1个感染者在每个传染期会接触到 个新人,这 人中有 个人接种过疫苗( 称为接种率),那么1个感染者新的传染人数为 .已知新冠病毒在某地的基本传染数 为了使1个感染者传染人数不超过1,该地疫苗的接种率至少为( )
A.40% B.50% C.60% D.70%
5.如图,直线 与单位圆相切于点 ,射线 从 出发,绕着点 逆时针旋转,在旋转的过程中,记 ( ), 所经过的单位圆 内区域(阴影部分)的面积为 ,记 ,则下列选项判断正确的是( )
A.当 时,
B.对任意 ,且 ,都有
C.对任意 ,都有
D.对任意 ,都有
6.某商店将进价为40元的商品按50元一件销售,一个月恰好卖500件,而价格每提高1元,就会少卖10个,商店为使该商品利润最大,应将每件商品定价为( )
A.50元 B.60元 C.70元 D.100元
二、多选题
7.据美国学者詹姆斯·马丁的测算,近十年,人类知识总量已达到每三年翻一番,到2020年甚至要达到每73天翻一番的空前速度.因此,基础教育的任务已不是教会一切人一切知识,而是让一切人学会学习.已知2000年底,人类知识总量为a ,假如从2000年底到2009年底是每三年翻一番,从2009年底到2019年底是每一年翻一番,2020年(按365天计算)是每73天翻一番,则下列说法正确的是( )
A.2006年底人类知识总量是2a B.2009年底人类知识总量是8a
C.2019年底人类知识总量是213a D.2020年底人类知识总量是218a
三、填空题
8.某食品的保鲜时间y(单位:小时)与储存温度x(单位: )满足函数关系 ( 为自然对数的底数,k、b为常数)。若该食品在0 的保鲜时间设计192小时,在22 的保鲜时间是48小时,则该食品在33 的保鲜时间是 小时.
9.如图,某人计划用篱笆围成一个一边靠墙(墙的长度没有限制)的矩形菜园.设菜园的长为米,宽为米.若菜园面积为平方米,则所用篱笆总长的最小值为 ;若使用的篱笆总长度为米,则的最小值为
10.某商场销售某种商品的经验表明,该产品生产总成本 与产量 的函数关系式为 ,销售单价 与产量 的函数关系式为 .要使每件产品的平均利润最大,则产量 等于 .
11.衣柜里的樟脑丸随着时间推移会挥发而体积变小,若它的体积 随时间 的变化规律是 ( 为自然对数的底),其中 为初始值.若 ,则 的值约为 .(运算结果保留整数,参考数据:
12.如图,天花板上悬挂着灯管 , ,灯线 ,为了提高灯管高度,将灯管 绕过 中点 的铅垂线 旋转 ,则该灯管升高了 .
四、解答题
13.随着社会发展,垃圾分类对改善和保护人类生活环境意义重大.某可回收废品处理厂响应国家环保部门的政策,引进新设备,废品处理能力大大提高.已知该厂每月的废品月处理成本 (元)与月处理量 (千吨)之间近似地的构成二次函数关系,经调研发现,该厂每月处理量 最少100千吨,最多500千吨.当月处理量为200千吨时,月处理成本最低,为50000元,且在月处理量最少的情况下,耗费月处理成本60000元.
(1)求月处理成本 (元)与月处理量 (千吨)之间函数关系式;
(2)该厂每月废品处理量为多少千吨时,才能使每千吨的处理成本最低?
(3)若该厂每处理一千吨废品获利400元,则每月能否获利?若获利,求出最大利润.
14.一批救灾物资随51辆汽车从某市以 的速度匀速直达灾区.已知两地公路线长 ,为了安全起见,两辆汽车的间距不得小于 ,那么这批物资全部到达灾区最少需要多长时间?
15.生命在于运动,运动在于锻炼.其中,游泳就是一个非常好的锻炼方式.游泳有众多好处:强.身健体;保障生命安全;增强心肺功能;锻炼意志,培养勇敢顽强精神;休闲娱乐,促进身心健康.近几年,游泳池成了新小区建设的标配.家门口的“游泳池”,成了市民休闲娱乐的好去处.如图,某小区规划一个深度为,底面积为的矩形游泳池,按规划要求:在游泳池的四周安排宽的休闲区,休闲区造价为元,游泳池的底面与墙面铺设瓷砖,瓷砖造价为元.其他设施等支出大约为万元,设游泳池的长为.
(1)试将总造价(元)表示为长度的函数;
(2)当取何值时,总造价最低,并求出最低总造价.
16.某公司今年一月份推出新产品A,其成本价为492元/件,经试销调查,销售量与销售价的关系如下表:
销售价(x/元件) 650 662 720 800
销售量(y件) 350 333 281 200
由此可知,销售量y(件)与销售价x(元/件)可近似看作一次函数y=kx+b的关系(通常取表中相距较远的两组数据所得一次函数较为精确).
(1)写出以x为自变量的函数y的解析式及定义域;
(2)试问:销售价定为多少时,一月份销售利润最大?并求最大销售利润和此时的销售量.
17.榆林市政府坚持保护环境和节约资源,坚持推进生态文明建设。若市财政局下拨专款100百万元,分别用于植绿护绿和处理污染两个生态维护项目,植绿护绿项目五年内带来的生态收益可表示为投放资金 (单位:百万元)的函数 (单位:百万元): ,处理污染项目五年内带来的生态收益可表示为投放资金 单位:(单位:百万元)的函数 (单位:百万元): 。
(1)设分配给植绿护绿项目的资金为 (百万元),则两个生态项目五年内带来的收益总和为y,写出y关于 的函数解析式和定义域;
(2)试求出y的最大值,并求出此时对两个生态项目的投资分别为多少?
18.如图,一载着重危病人的火车从地出发,沿北偏东射线行驶,其中,在距离地10公里北偏东角的处住有一位医学专家(其中),现有紧急征调离地正东公里的处的救护车赶往处载上医学专家全速追赶乘有重危病人的火车,并在处相遇,经计算当两车行驶的路线与围成的三角形面积最小时,抢救最及时.
(1)求关于的函数关系;
(2)当为何值时,抢救最及时.
答案解析部分
1.【答案】C
【知识点】根据实际问题选择函数类型
2.【答案】B
【知识点】根据实际问题选择函数类型
3.【答案】C
【知识点】函数模型的选择与应用
4.【答案】C
【知识点】函数模型的选择与应用
5.【答案】C
【知识点】函数模型的选择与应用
6.【答案】C
【知识点】函数模型的选择与应用
7.【答案】B,C,D
【知识点】函数模型的选择与应用
8.【答案】24
【知识点】函数模型的选择与应用
9.【答案】20;
【知识点】函数的最大(小)值;函数模型的选择与应用
10.【答案】40
【知识点】基本不等式在最值问题中的应用;函数模型的选择与应用
11.【答案】11
【知识点】函数模型的选择与应用
12.【答案】10
【知识点】函数模型的选择与应用
13.【答案】(1)解:由题意知:设该二次函数为 ,
当 时, ,
即 ,
解得: ,
,
故月处理成本 (元)与月处理量 (千吨)之间函数关系式为: ;
(2)由题意知每千吨的月处理成本:
,
当且仅当 时,即当 时, 有最小值200,
故该厂每月废品处理量为300千吨时,才能使每千吨的处理成本最低;
(3)设该厂每月利润 元,则由题意:
,
故当 时, 有最大值70000,即每月最大利润为70000元,
故能获利,最大利润为70000元.
【知识点】函数的最大(小)值;根据实际问题选择函数类型
14.【答案】当最后一辆车子出发时,第一辆车子走了 小时,
最后一辆车走完全程共需要 小时,
所以一共需要 小时,
由基本不等式 ,当且仅当 ,即 时等号成立,
故最少需要10小时.
【知识点】根据实际问题选择函数类型;基本不等式在最值问题中的应用
15.【答案】(1)解:因为游泳池的长为,所以游泳池的宽为,
铺游泳池的花费为,
休闲区的花费为,
所以,总造价为,其中;
(2)解:由基本不等式可得
(元),
当且仅当时,等号成立.
因此,当时,总造价最低,且最低总造价为元.
【知识点】根据实际问题选择函数类型;基本不等式
16.【答案】(1)解:由题意知 ,
解得k=﹣1,b=1000,∴y=﹣x+1000
由于y为非负整数,所以0≤x≤1000
(2)解:设一月份的利润为S元,由题意得S=(x﹣492)(1000﹣x)=﹣(x﹣746)2+64516
∴当x=746元/件时,一月份销售收入 最大为64516元
【知识点】函数模型的选择与应用
17.【答案】(1)解:由题意可得处理污染项目投放资金为 百万元,
所以 ,
∴ , ;
所以 ,
(2)解:由(1)得
当且仅当 ,即 时等号成立,
此时 .
∴y的最大值为52百万元,分别投资给植绿护绿项目、污染处理项目的资金为40百万元,60百万元.
【知识点】基本不等式在最值问题中的应用;函数模型的选择与应用
18.【答案】(1)解:建立如图所示的直角坐标系,
因为,所以,
因为,所以,
因为,所以射线的方程为,
因为,所以直线的斜率为(),
所以直线的方程为(),
当时,点,则,
当时,由,得(),
所以点(),
所以(),
综上,当时,,当且时,
(2)解:由(1)得当且时,
,
当且仅当,即时取等号,
而当时,,
所以当时,有最小值,即抢救最及时
【知识点】基本不等式在最值问题中的应用;函数模型的选择与应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
