【高中数学北师大版必修第一册同步练习】 3用样本估计总体分布(含答案)
文档属性
| 名称 | 【高中数学北师大版必修第一册同步练习】 3用样本估计总体分布(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-03 07:32:18 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【高中数学北师大版必修第一册同步练习】
3用样本估计总体分布
一、单选题
1.某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( ).
A.45 B.60 C.75 D.90
2.某校高三年级的全体学生参加体育测试,成绩的频率分布直方图如图,数据的分组依次为: , , , .若低于60分的人数是90,则该校高三年级的学生人数是( )
A.270 B.300 C.330 D.360
3.一个容量为100的样本分成若干组,已知某组的频率为0.3,则该组的频数是( )
A.3 B.30 C.10 D.300
4.在样本的频率分布直方图中,共有11个小长方形,若中间一个长方形的面积等于其他十个小长方形面积的和的 ,且样本容量是160,则中间一组的频数为( )
A.32 B.0.2 C.40 D.0.25
二、多选题
5.某学校组织了一次劳动技能大赛,共有100名学生参赛,经过评判,这100名参赛者的得分都在内,得分60分以下为不及格,其得分的频率分布直方图如图所示(按得分分成,,,,这五组),则下列结论正确的是( )
A.直方图中
B.此次比赛得分及格的共有55人
C.以频率为概率,从这100名参赛者中随机选取1人,其得分在[50,80)的概率为0.75
D.这100名参赛者得分的第80百分位数为75
三、填空题
6. 某电子商务公司对10000名网络购物者2014年度的消费情况进行统计,发现消费金额
(单位:万元)都在区间内,其频率分布直方图如图所示.
(Ⅰ)直方图中的 ;
(Ⅱ)在这些购物者中,消费金额在区间内的购物者的人数为 .
7.抽取样本容量为20的样本数据,分组后的频数如下表:
分组
频数 2 3 4 5 4 2
则样本数据落在区间 的频率为 .
8.在样本的频率分布直方图中,共有 个小长方形,若中间一个长方形的面积等于其他 个小长方形面积的和的 ,且样本容量为 ,则中间一组的频数为 .
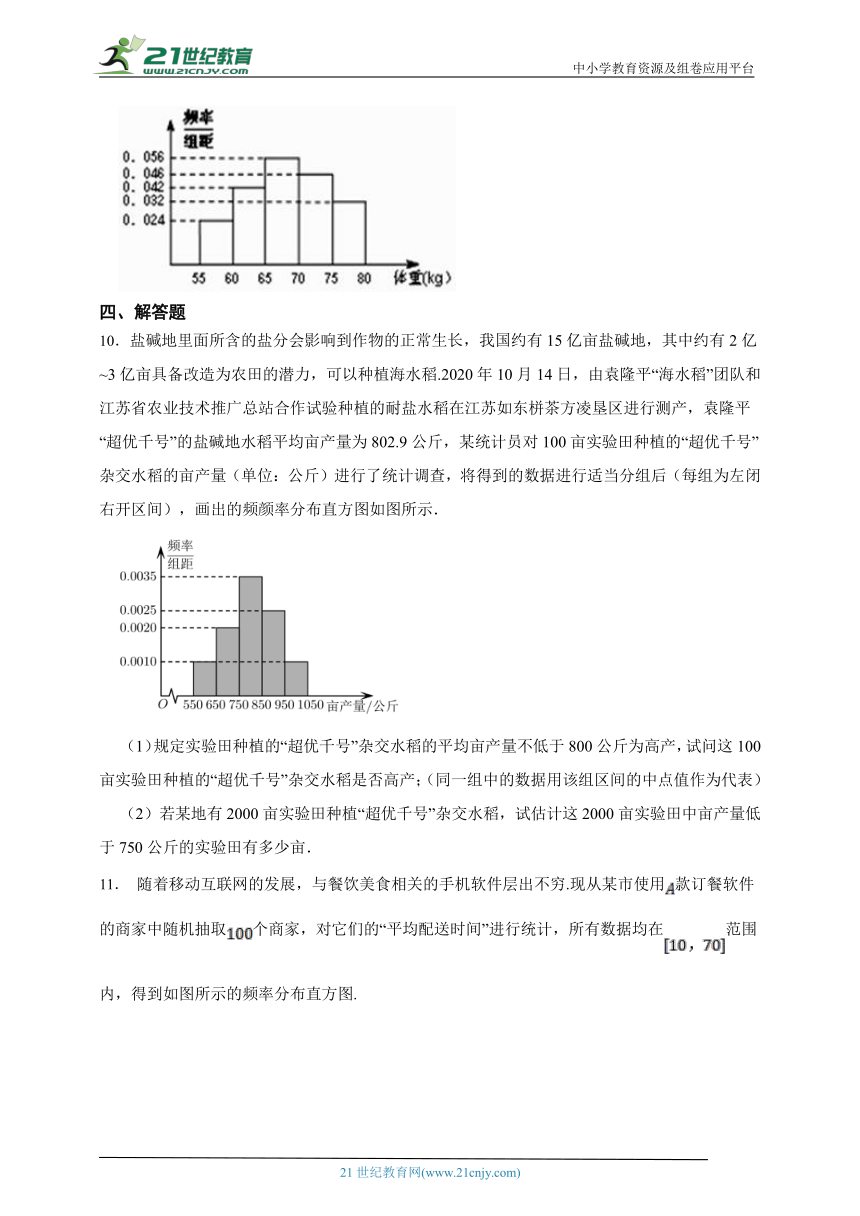
9.对某学校n名学生的体重进行统计,得到频率分布直方图如图所示,则体重在75kg以上的学生人数为32人,则n= .
四、解答题
10.盐碱地里面所含的盐分会影响到作物的正常生长,我国约有15亿亩盐碱地,其中约有2亿~3亿亩具备改造为农田的潜力,可以种植海水稻.2020年10月14日,由袁隆平“海水稻”团队和江苏省农业技术推广总站合作试验种植的耐盐水稻在江苏如东栟茶方凌垦区进行测产,袁隆平“超优千号”的盐碱地水稻平均亩产量为802.9公斤,某统计员对100亩实验田种植的“超优千号”杂交水稻的亩产量(单位:公斤)进行了统计调查,将得到的数据进行适当分组后(每组为左闭右开区间),画出的频颜率分布直方图如图所示.
(1)规定实验田种植的“超优千号”杂交水稻的平均亩产量不低于800公斤为高产,试问这100亩实验田种植的“超优千号”杂交水稻是否高产;(同一组中的数据用该组区间的中点值作为代表)
(2)若某地有2000亩实验田种植“超优千号”杂交水稻,试估计这2000亩实验田中亩产量低于750公斤的实验田有多少亩.
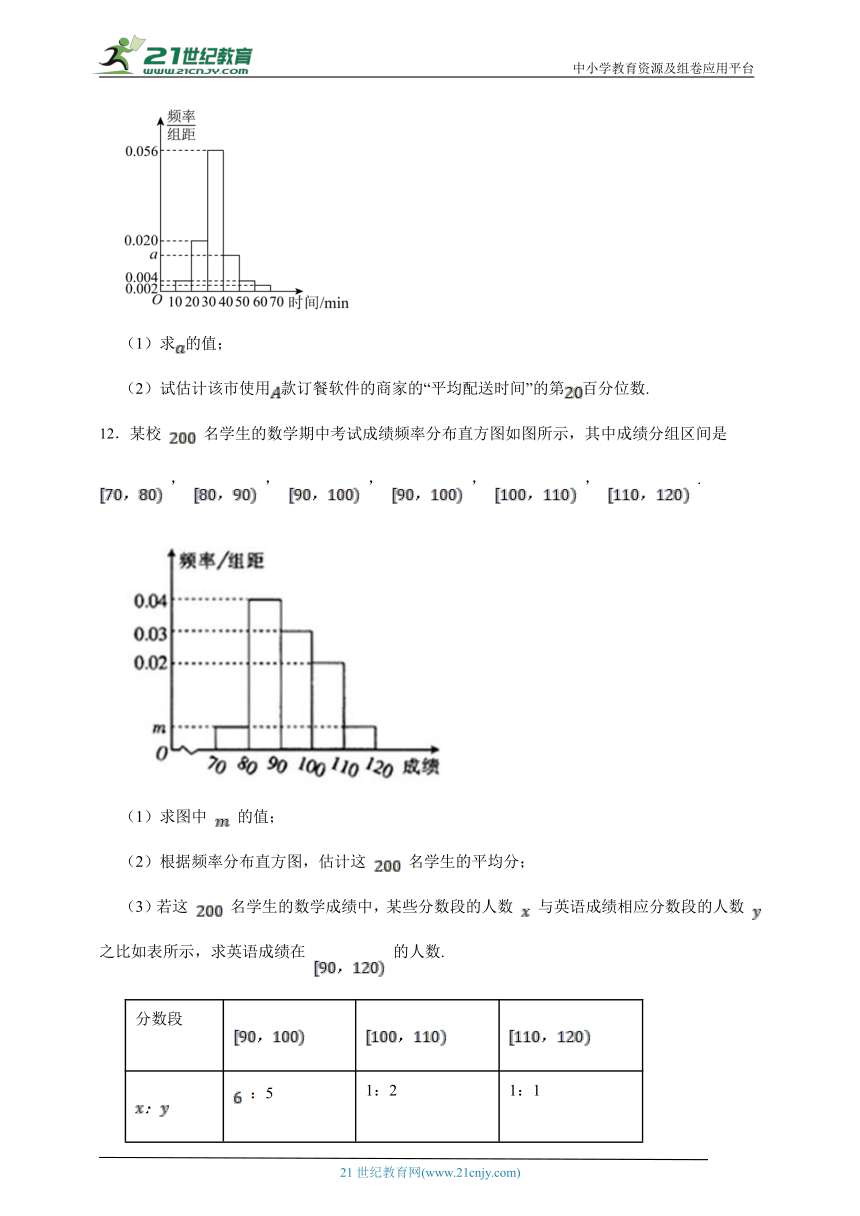
11. 随着移动互联网的发展,与餐饮美食相关的手机软件层出不穷.现从某市使用款订餐软件的商家中随机抽取个商家,对它们的“平均配送时间”进行统计,所有数据均在范围内,得到如图所示的频率分布直方图.
(1)求的值;
(2)试估计该市使用款订餐软件的商家的“平均配送时间”的第百分位数.
12.某校 名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是 , , , , , .
(1)求图中 的值;
(2)根据频率分布直方图,估计这 名学生的平均分;
(3)若这 名学生的数学成绩中,某些分数段的人数 与英语成绩相应分数段的人数 之比如表所示,求英语成绩在 的人数.
分数段
:5 1:2 1:1
13.销售某种活海鲜,按日需量 (公斤)属于 , , , , 进行分组,得到如图所示的频率分布直方图.这种海鲜经销商进价成本为每公斤20元,已知进货当天以每公斤30元进行销售,当天未售出的须全部以每公斤10元卖给冷冻库.某海鲜产品经销商某天购进了300公斤这种海鲜,设当天利润为 元.
(1)根据直方图,估计日需量 (公斤)平均数.
(2)求 关于 的函数关系式并结合直方图估计利润 不小于800元的概率.
14.海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:
(1)记A表示事件“旧养殖法的箱产量低于50kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg 箱产量≥50kg
旧养殖法
新养殖法
(3)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行较。
附:
P(K2≥k) 0.050 0.010 0.001
k 3.841 6.635 10.828
15.某城市 户居民的月平均用电量(单位:度),以 , , , , , , 分组的频率分布直方图如图.
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为 , , , 的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在 的用户中应抽取多少户?
答案解析部分
1.【答案】D
【知识点】频率分布直方图
2.【答案】B
【知识点】频率分布直方图
3.【答案】B
【知识点】频率分布表
4.【答案】A
【知识点】频率分布直方图
5.【答案】A,D
【知识点】频率分布直方图
6.【答案】3;6000
【知识点】频率分布直方图
7.【答案】0.25
【知识点】频率分布表
8.【答案】
【知识点】频率分布直方图
9.【答案】200
【知识点】频率分布直方图
10.【答案】(1)解:该实验田种植的“超优千号”杂交水稻的平均亩产量为,所以这100亩实验田种植的“超优千号”杂交水稻高产.
(2)解:该实验田中亩产量低于750的频率为,
所以2000亩实验田中亩产量低于750公斤的实验田有亩.
【知识点】频率分布直方图
11.【答案】(1)解:依题意可得,
解得.
(2)解:因为,所以第百分位数位于之间,
设为,则,解得,
故第百分位数为.
【知识点】频率分布直方图
12.【答案】(1)解:由 ,
解得 .
(2)解:频率分布直方图中每一个小矩形的面积乘以底边中点的横坐标之和即为平均数,
即估计平均数为 .
(3)解:由频率分布直方图可求出这 名学生的数学成绩在 , , 的分别有 人, 人, 人,按照表中给的比例,则英语成绩在 , , 的分别有 人, 人, 人,所以英语成绩在 的有 人.
【知识点】频率分布直方图
13.【答案】(1)解:
日需求量平均值大约是265公斤.
(2)解:当日需求量不低于300公斤时,利润 元;
当日需求量不足300公斤时,利润 (元);
故 .
由 得, ,
∴
或者
【知识点】频率分布直方图
14.【答案】(1)解:旧养殖法的箱产量低于50kg的频率为
(0.012+0.014+0.024+0.034+0.040)×5=0.62.
因此,事件A的概率估计值为0.62.
(2)解:根据箱产量的频率分布直方图得列联表
箱产量<50kg 箱产量≥50kg
旧养殖法 62 38
新养殖法 34 66
K2的观测值k= ≈15.705.
由于15.705>6.635,故有99%的把握认为箱产量与养殖方法有关
(3)解:箱产量的频率分布直方图表明:新养殖法的箱产量平均值(或中位数)在50kg到55kg之间,旧养殖法的箱产量平均值(或中位数)在45kg到50kg之间,且新养殖法的箱产量分布集中程度较旧养殖法的箱产量分布集中程度高,因此,可以认为新养殖法的箱产量较高且稳定,从而新养殖法优于旧养殖法.
【知识点】频率分布直方图
15.【答案】(1)解:由直方图的性质可得(0.002+0.0095+0.011+0.0125+x+0.005+0.0025)×20=1得:
x=0.0075,所以直方图中x的值是0.0075.
(2)解:月平均用电量的众数是 =230因为(0.002+0.0095+0.011)×20=0.45<0.5,所以月平均用电量的中位数在[220,240)内,
设中位数为a,
由(0.002+0.0095+0.011)×20+0.0125×(a-220)=0.5
得:a=224,所以月平均用电量的中位数是224
(3)解:月平均用电量为[220,240]的用户有0.0125×20×100=25户,
月平均用电量为[240,260)的用户有0.0075×20×100=15户,
月平均用电量为[260,280)的用户有0. 005×20×100=10户,
月平均用电量为[280,300]的用户有0.0025×20×100=5户,
抽取比例= = ,所以月平均用电量在[220,240)的用户中应抽取25× =5户
【知识点】频率分布直方图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【高中数学北师大版必修第一册同步练习】
3用样本估计总体分布
一、单选题
1.某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( ).
A.45 B.60 C.75 D.90
2.某校高三年级的全体学生参加体育测试,成绩的频率分布直方图如图,数据的分组依次为: , , , .若低于60分的人数是90,则该校高三年级的学生人数是( )
A.270 B.300 C.330 D.360
3.一个容量为100的样本分成若干组,已知某组的频率为0.3,则该组的频数是( )
A.3 B.30 C.10 D.300
4.在样本的频率分布直方图中,共有11个小长方形,若中间一个长方形的面积等于其他十个小长方形面积的和的 ,且样本容量是160,则中间一组的频数为( )
A.32 B.0.2 C.40 D.0.25
二、多选题
5.某学校组织了一次劳动技能大赛,共有100名学生参赛,经过评判,这100名参赛者的得分都在内,得分60分以下为不及格,其得分的频率分布直方图如图所示(按得分分成,,,,这五组),则下列结论正确的是( )
A.直方图中
B.此次比赛得分及格的共有55人
C.以频率为概率,从这100名参赛者中随机选取1人,其得分在[50,80)的概率为0.75
D.这100名参赛者得分的第80百分位数为75
三、填空题
6. 某电子商务公司对10000名网络购物者2014年度的消费情况进行统计,发现消费金额
(单位:万元)都在区间内,其频率分布直方图如图所示.
(Ⅰ)直方图中的 ;
(Ⅱ)在这些购物者中,消费金额在区间内的购物者的人数为 .
7.抽取样本容量为20的样本数据,分组后的频数如下表:
分组
频数 2 3 4 5 4 2
则样本数据落在区间 的频率为 .
8.在样本的频率分布直方图中,共有 个小长方形,若中间一个长方形的面积等于其他 个小长方形面积的和的 ,且样本容量为 ,则中间一组的频数为 .
9.对某学校n名学生的体重进行统计,得到频率分布直方图如图所示,则体重在75kg以上的学生人数为32人,则n= .
四、解答题
10.盐碱地里面所含的盐分会影响到作物的正常生长,我国约有15亿亩盐碱地,其中约有2亿~3亿亩具备改造为农田的潜力,可以种植海水稻.2020年10月14日,由袁隆平“海水稻”团队和江苏省农业技术推广总站合作试验种植的耐盐水稻在江苏如东栟茶方凌垦区进行测产,袁隆平“超优千号”的盐碱地水稻平均亩产量为802.9公斤,某统计员对100亩实验田种植的“超优千号”杂交水稻的亩产量(单位:公斤)进行了统计调查,将得到的数据进行适当分组后(每组为左闭右开区间),画出的频颜率分布直方图如图所示.
(1)规定实验田种植的“超优千号”杂交水稻的平均亩产量不低于800公斤为高产,试问这100亩实验田种植的“超优千号”杂交水稻是否高产;(同一组中的数据用该组区间的中点值作为代表)
(2)若某地有2000亩实验田种植“超优千号”杂交水稻,试估计这2000亩实验田中亩产量低于750公斤的实验田有多少亩.
11. 随着移动互联网的发展,与餐饮美食相关的手机软件层出不穷.现从某市使用款订餐软件的商家中随机抽取个商家,对它们的“平均配送时间”进行统计,所有数据均在范围内,得到如图所示的频率分布直方图.
(1)求的值;
(2)试估计该市使用款订餐软件的商家的“平均配送时间”的第百分位数.
12.某校 名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是 , , , , , .
(1)求图中 的值;
(2)根据频率分布直方图,估计这 名学生的平均分;
(3)若这 名学生的数学成绩中,某些分数段的人数 与英语成绩相应分数段的人数 之比如表所示,求英语成绩在 的人数.
分数段
:5 1:2 1:1
13.销售某种活海鲜,按日需量 (公斤)属于 , , , , 进行分组,得到如图所示的频率分布直方图.这种海鲜经销商进价成本为每公斤20元,已知进货当天以每公斤30元进行销售,当天未售出的须全部以每公斤10元卖给冷冻库.某海鲜产品经销商某天购进了300公斤这种海鲜,设当天利润为 元.
(1)根据直方图,估计日需量 (公斤)平均数.
(2)求 关于 的函数关系式并结合直方图估计利润 不小于800元的概率.
14.海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:
(1)记A表示事件“旧养殖法的箱产量低于50kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg 箱产量≥50kg
旧养殖法
新养殖法
(3)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行较。
附:
P(K2≥k) 0.050 0.010 0.001
k 3.841 6.635 10.828
15.某城市 户居民的月平均用电量(单位:度),以 , , , , , , 分组的频率分布直方图如图.
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为 , , , 的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在 的用户中应抽取多少户?
答案解析部分
1.【答案】D
【知识点】频率分布直方图
2.【答案】B
【知识点】频率分布直方图
3.【答案】B
【知识点】频率分布表
4.【答案】A
【知识点】频率分布直方图
5.【答案】A,D
【知识点】频率分布直方图
6.【答案】3;6000
【知识点】频率分布直方图
7.【答案】0.25
【知识点】频率分布表
8.【答案】
【知识点】频率分布直方图
9.【答案】200
【知识点】频率分布直方图
10.【答案】(1)解:该实验田种植的“超优千号”杂交水稻的平均亩产量为,所以这100亩实验田种植的“超优千号”杂交水稻高产.
(2)解:该实验田中亩产量低于750的频率为,
所以2000亩实验田中亩产量低于750公斤的实验田有亩.
【知识点】频率分布直方图
11.【答案】(1)解:依题意可得,
解得.
(2)解:因为,所以第百分位数位于之间,
设为,则,解得,
故第百分位数为.
【知识点】频率分布直方图
12.【答案】(1)解:由 ,
解得 .
(2)解:频率分布直方图中每一个小矩形的面积乘以底边中点的横坐标之和即为平均数,
即估计平均数为 .
(3)解:由频率分布直方图可求出这 名学生的数学成绩在 , , 的分别有 人, 人, 人,按照表中给的比例,则英语成绩在 , , 的分别有 人, 人, 人,所以英语成绩在 的有 人.
【知识点】频率分布直方图
13.【答案】(1)解:
日需求量平均值大约是265公斤.
(2)解:当日需求量不低于300公斤时,利润 元;
当日需求量不足300公斤时,利润 (元);
故 .
由 得, ,
∴
或者
【知识点】频率分布直方图
14.【答案】(1)解:旧养殖法的箱产量低于50kg的频率为
(0.012+0.014+0.024+0.034+0.040)×5=0.62.
因此,事件A的概率估计值为0.62.
(2)解:根据箱产量的频率分布直方图得列联表
箱产量<50kg 箱产量≥50kg
旧养殖法 62 38
新养殖法 34 66
K2的观测值k= ≈15.705.
由于15.705>6.635,故有99%的把握认为箱产量与养殖方法有关
(3)解:箱产量的频率分布直方图表明:新养殖法的箱产量平均值(或中位数)在50kg到55kg之间,旧养殖法的箱产量平均值(或中位数)在45kg到50kg之间,且新养殖法的箱产量分布集中程度较旧养殖法的箱产量分布集中程度高,因此,可以认为新养殖法的箱产量较高且稳定,从而新养殖法优于旧养殖法.
【知识点】频率分布直方图
15.【答案】(1)解:由直方图的性质可得(0.002+0.0095+0.011+0.0125+x+0.005+0.0025)×20=1得:
x=0.0075,所以直方图中x的值是0.0075.
(2)解:月平均用电量的众数是 =230因为(0.002+0.0095+0.011)×20=0.45<0.5,所以月平均用电量的中位数在[220,240)内,
设中位数为a,
由(0.002+0.0095+0.011)×20+0.0125×(a-220)=0.5
得:a=224,所以月平均用电量的中位数是224
(3)解:月平均用电量为[220,240]的用户有0.0125×20×100=25户,
月平均用电量为[240,260)的用户有0.0075×20×100=15户,
月平均用电量为[260,280)的用户有0. 005×20×100=10户,
月平均用电量为[280,300]的用户有0.0025×20×100=5户,
抽取比例= = ,所以月平均用电量在[220,240)的用户中应抽取25× =5户
【知识点】频率分布直方图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
