21.2 解一元二次方程 课件 人教版九年级上册第二十一章 一元二次方程
文档属性
| 名称 | 21.2 解一元二次方程 课件 人教版九年级上册第二十一章 一元二次方程 |  | |
| 格式 | pptx | ||
| 文件大小 | 602.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-04 09:33:04 | ||
图片预览







文档简介
(共28张PPT)
21.2 解一元二次方程
2024—2025学年人教版
九年级上册
第二十一章 一元二次方程
前面学习了方程ax2+bx+c=0 (a≠0) 的求根公式不仅表示可以由方程的系数a,b,c决定根的值,而且反映了根与系数之间的联系.一元二次方程根与系数之间还有什么关系呢?
x-x1)(x-x2)=0(两根x1,x2)
x2+px+q=0
x1+x2=-p
x1x2=q
知识回顾
根据求根公式可知,
由此可知
根与系数
的关系
了解分解因式法解一元二次方程的概念,并会用分解因式法解某些一元二次方程.
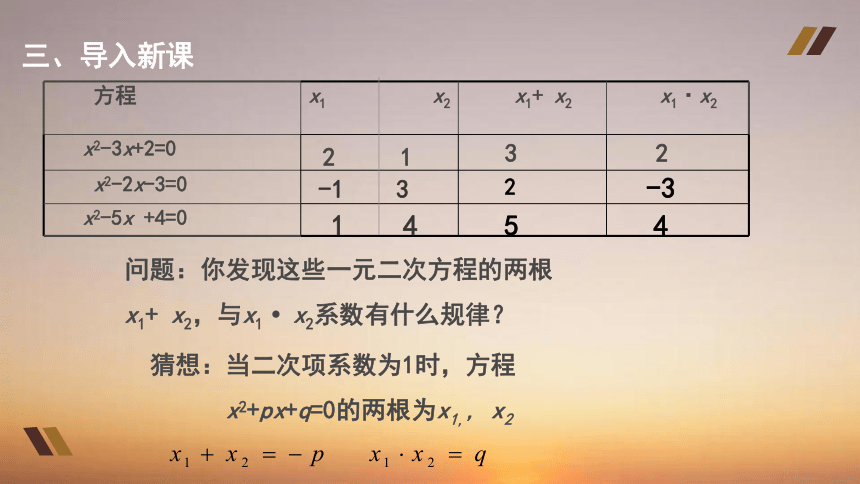
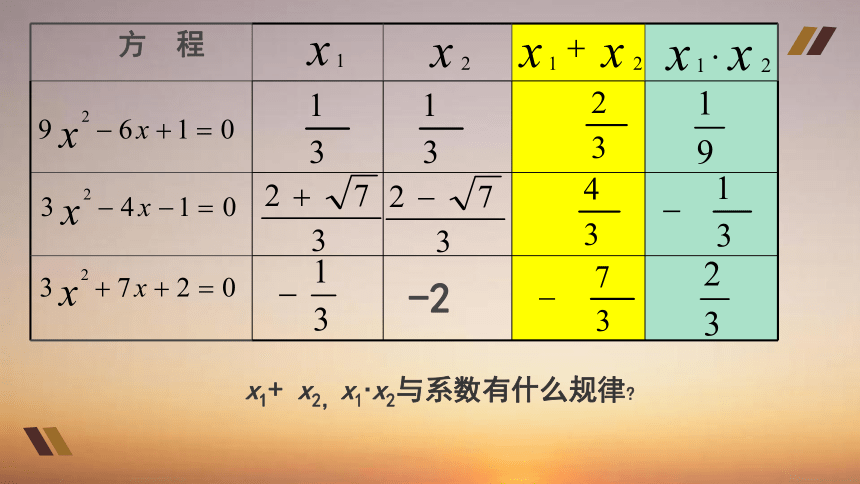
方程 x1 x2 x1+ x2 x1·x2
x2-3x+2=0
x2-2x-3=0
x2-5x +4=0
问题:你发现这些一元二次方程的两根
x1+ x2,与x1 x2系数有什么规律?
猜想:当二次项系数为1时,方程
x2+px+q=0的两根为x1,, x2
2 1
3
2
-1 3
2
-3
1 4
5
4
三、导入新课
方 程
-2
x1+ x2,x1 x2与系数有什么规律
求根公式的推导
合作探究
用配方法解一般形式的一元二次方程 ax2+bx+c=0 (a≠0).
二次项系数化为1,得
解:
移项,得
配方,得
即 ①
问题:对于方程①接下来能用直接开平方解吗?
∵a ≠0,∴4a2>0.
式子b2-4ac 的值有一下三种情况:
(1)b2-4ac >0,
这时 >0,由①得
方程有两个不等的实数根
(2)b2-4ac =0
这时 =0,由①可知,方程有两个相等的实数根 x1=x2=- .
(3)b2-4ac <0
这时 <0,由①可知 <0 ,而x取任何实数都不能使 <0 ,因此方程无实数根.
两个不相等的实数根
两个相等的实数根
没有实数根
两个实数根
判别式的情况
根的情况
我们把b2-4ac叫做一元二次方程ax2+bx+c=0根的判别式,通常用符号“ ”表示,即 = b2-4ac.
> 0
= 0
< 0
≥ 0
一元二次方程根的判别式
按要求完成下列表格:
练一练
的值
0
4
根的 情况
有两个相等的实数根
没有实数根
有两个不相等的实数根
例1 已知一元二次方程x2+x=1,下列判断正确的是( )
A.该方程有两个相等的实数根
B.该方程有两个不相等的实数根
C.该方程无实数根
D.该方程根的情况不确定
解析:原方程变形为x2+x-1=0.∵b2-4ac=1-4×1×(-1)=
5>0,∴该方程有两个不相等的实数根,故选B.
B
典例精析
例2 不解方程,判断下列方程的根的情况.
(1)3x2+4x-3=0; (2)4x2=12x-9;
解:(1)3x2+4x-3=0,a=3,b=4,c=-3,
∴b2-4ac=42-4×3×(-3)=52>0.
∴方程有两个不相等的实数根.
(2)方程化为:4x2-12x+9=0,
∴b2-4ac=(-12)2-4×4×9=0.
∴方程有两个相等的实数根.
(3) 7y=5(y2+1).
解:(3)方程化为:5y2-7y+5=0,
∴b2-4ac=(-7)2-4×5×5=-51<0.
∴方程无实数根.
方法归纳
判断一元二次方程根的情况的方法:
b2 - 4ac > 0
b2 - 4ac = 0
b2 - 4ac< 0
有两个不相等的实数根
有两个相等的实数根
没有实数根
例3 若关于x的一元二次方程x2+8x+q=0有两个不相等的实数根,则q的取值范围是( )
A.q≤4 B.q≥4
C.q<16 D.q>16
C
析:由根的判别式知,方程有两个不相等的实数根,则b2-4ac>0,即 .解得q<16,故选C.
典例精析
【变式题】二次项系数含字母
若关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根,则k的取值范围是( )
A.k>-1 B.k>-1且k≠0
C.k<1 D.k<1且k≠0
B
当一元二次方程二次项系数为字母时,一定要注意二次项系数不为0,再根据根的判别式求字母的取值范围.
归纳
方程有两个不相等的实数根
分析:
二次项系数不为0
k≠0
k>-1且k≠0
【变式题】删除限制条件“二次”
若关于x的方程kx2-2x-1=0有实数根,则k的取值范围是( )
A.k≥-1 B.k≥-1且k≠0
C.k<1 D.k<1且k≠0
分析:
分类讨论
k=0
k≠0
原方程变形为-2x-1=0,有实数根
b2-4ac≥0
k≥-1
A
由上可知,当 ≥0时,方程ax2+bx+c=0 (a≠0)的实数根可写为 的形式,这个式子叫做一元二次方程ax2+bx+c=0 的求根公式.
注意
运用公式法解一元二次方程时,首先要将方程化为一般式,判定b2 - 4ac ≥0时,才可以用求根公式.
用求根公式解一元二次方程的方法叫做公式法.
用公式法解方程
例4 用公式法解下列方程:
典例精析
(1)x2-4x-7=0;
方程有两个不相等的实数根.
解:a=1,b=-4,c=-7
b2-4ac=(-4)2-4×1×(-7)=44>0.
即
方程有两个相等的实数根
x1=x2
(3)5x2-3x=x+1;
方程有两个不相等的实数根
=
即
a=5,b=-4,c=-1
b2-4ac=(-4)2-4×5×(-1)=36>0.
解:方程化为 5x2-4x-1=0
(4)x2+17=8x.
方程无实数根.
a=1,b=-8,c=17
b2-4ac=(-8)2-4×1×17=-4<0.
解:方程化为 x2-8x+17=0
要点归纳
公式法解方程的步骤
1.变形:化已知方程为一般形式;
2.确定系数:用a,b,c写出各项系数;
3.计算:b2-4ac的值;
4.判断:若b2-4ac ≥0,则利用求根公式求出;
若b2-4ac<0,则方程没有实数根.
x2-5x+6=0
课堂练习:
1.甲、乙二人解同一个一元二次方程时,甲看错了常数项所求出的根为1,4;乙看错了一次项系数所求出的根是-2,-3。则这个一元二次方程为_____________________
(还有其他解法吗?)
-3
3、已知3是方程 x2-mx-3=0的一根,求m及另一根.
3
2
2、如果-1是方程的一个根,2x2-x+m=0则另一个根是____ m=____。
1、熟练掌握根与系数的关系;
2、灵活运用根与系数关系解决问题;
3、探索解题思路,归纳解题思想方法。
课堂小结
一正根,一负根
△>0
X1X2<0
两个正根
△≥0
X1X2>0
X1+X2>0
两个负根
△≥0
X1X2>0
X1+X2<0
{
{
{
21.2 解一元二次方程
谢 谢 聆 听
21.2 解一元二次方程
2024—2025学年人教版
九年级上册
第二十一章 一元二次方程
前面学习了方程ax2+bx+c=0 (a≠0) 的求根公式不仅表示可以由方程的系数a,b,c决定根的值,而且反映了根与系数之间的联系.一元二次方程根与系数之间还有什么关系呢?
x-x1)(x-x2)=0(两根x1,x2)
x2+px+q=0
x1+x2=-p
x1x2=q
知识回顾
根据求根公式可知,
由此可知
根与系数
的关系
了解分解因式法解一元二次方程的概念,并会用分解因式法解某些一元二次方程.
方程 x1 x2 x1+ x2 x1·x2
x2-3x+2=0
x2-2x-3=0
x2-5x +4=0
问题:你发现这些一元二次方程的两根
x1+ x2,与x1 x2系数有什么规律?
猜想:当二次项系数为1时,方程
x2+px+q=0的两根为x1,, x2
2 1
3
2
-1 3
2
-3
1 4
5
4
三、导入新课
方 程
-2
x1+ x2,x1 x2与系数有什么规律
求根公式的推导
合作探究
用配方法解一般形式的一元二次方程 ax2+bx+c=0 (a≠0).
二次项系数化为1,得
解:
移项,得
配方,得
即 ①
问题:对于方程①接下来能用直接开平方解吗?
∵a ≠0,∴4a2>0.
式子b2-4ac 的值有一下三种情况:
(1)b2-4ac >0,
这时 >0,由①得
方程有两个不等的实数根
(2)b2-4ac =0
这时 =0,由①可知,方程有两个相等的实数根 x1=x2=- .
(3)b2-4ac <0
这时 <0,由①可知 <0 ,而x取任何实数都不能使 <0 ,因此方程无实数根.
两个不相等的实数根
两个相等的实数根
没有实数根
两个实数根
判别式的情况
根的情况
我们把b2-4ac叫做一元二次方程ax2+bx+c=0根的判别式,通常用符号“ ”表示,即 = b2-4ac.
> 0
= 0
< 0
≥ 0
一元二次方程根的判别式
按要求完成下列表格:
练一练
的值
0
4
根的 情况
有两个相等的实数根
没有实数根
有两个不相等的实数根
例1 已知一元二次方程x2+x=1,下列判断正确的是( )
A.该方程有两个相等的实数根
B.该方程有两个不相等的实数根
C.该方程无实数根
D.该方程根的情况不确定
解析:原方程变形为x2+x-1=0.∵b2-4ac=1-4×1×(-1)=
5>0,∴该方程有两个不相等的实数根,故选B.
B
典例精析
例2 不解方程,判断下列方程的根的情况.
(1)3x2+4x-3=0; (2)4x2=12x-9;
解:(1)3x2+4x-3=0,a=3,b=4,c=-3,
∴b2-4ac=42-4×3×(-3)=52>0.
∴方程有两个不相等的实数根.
(2)方程化为:4x2-12x+9=0,
∴b2-4ac=(-12)2-4×4×9=0.
∴方程有两个相等的实数根.
(3) 7y=5(y2+1).
解:(3)方程化为:5y2-7y+5=0,
∴b2-4ac=(-7)2-4×5×5=-51<0.
∴方程无实数根.
方法归纳
判断一元二次方程根的情况的方法:
b2 - 4ac > 0
b2 - 4ac = 0
b2 - 4ac< 0
有两个不相等的实数根
有两个相等的实数根
没有实数根
例3 若关于x的一元二次方程x2+8x+q=0有两个不相等的实数根,则q的取值范围是( )
A.q≤4 B.q≥4
C.q<16 D.q>16
C
析:由根的判别式知,方程有两个不相等的实数根,则b2-4ac>0,即 .解得q<16,故选C.
典例精析
【变式题】二次项系数含字母
若关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根,则k的取值范围是( )
A.k>-1 B.k>-1且k≠0
C.k<1 D.k<1且k≠0
B
当一元二次方程二次项系数为字母时,一定要注意二次项系数不为0,再根据根的判别式求字母的取值范围.
归纳
方程有两个不相等的实数根
分析:
二次项系数不为0
k≠0
k>-1且k≠0
【变式题】删除限制条件“二次”
若关于x的方程kx2-2x-1=0有实数根,则k的取值范围是( )
A.k≥-1 B.k≥-1且k≠0
C.k<1 D.k<1且k≠0
分析:
分类讨论
k=0
k≠0
原方程变形为-2x-1=0,有实数根
b2-4ac≥0
k≥-1
A
由上可知,当 ≥0时,方程ax2+bx+c=0 (a≠0)的实数根可写为 的形式,这个式子叫做一元二次方程ax2+bx+c=0 的求根公式.
注意
运用公式法解一元二次方程时,首先要将方程化为一般式,判定b2 - 4ac ≥0时,才可以用求根公式.
用求根公式解一元二次方程的方法叫做公式法.
用公式法解方程
例4 用公式法解下列方程:
典例精析
(1)x2-4x-7=0;
方程有两个不相等的实数根.
解:a=1,b=-4,c=-7
b2-4ac=(-4)2-4×1×(-7)=44>0.
即
方程有两个相等的实数根
x1=x2
(3)5x2-3x=x+1;
方程有两个不相等的实数根
=
即
a=5,b=-4,c=-1
b2-4ac=(-4)2-4×5×(-1)=36>0.
解:方程化为 5x2-4x-1=0
(4)x2+17=8x.
方程无实数根.
a=1,b=-8,c=17
b2-4ac=(-8)2-4×1×17=-4<0.
解:方程化为 x2-8x+17=0
要点归纳
公式法解方程的步骤
1.变形:化已知方程为一般形式;
2.确定系数:用a,b,c写出各项系数;
3.计算:b2-4ac的值;
4.判断:若b2-4ac ≥0,则利用求根公式求出;
若b2-4ac<0,则方程没有实数根.
x2-5x+6=0
课堂练习:
1.甲、乙二人解同一个一元二次方程时,甲看错了常数项所求出的根为1,4;乙看错了一次项系数所求出的根是-2,-3。则这个一元二次方程为_____________________
(还有其他解法吗?)
-3
3、已知3是方程 x2-mx-3=0的一根,求m及另一根.
3
2
2、如果-1是方程的一个根,2x2-x+m=0则另一个根是____ m=____。
1、熟练掌握根与系数的关系;
2、灵活运用根与系数关系解决问题;
3、探索解题思路,归纳解题思想方法。
课堂小结
一正根,一负根
△>0
X1X2<0
两个正根
△≥0
X1X2>0
X1+X2>0
两个负根
△≥0
X1X2>0
X1+X2<0
{
{
{
21.2 解一元二次方程
谢 谢 聆 听
同课章节目录
