8.3 简单几何体的表面积与体积(含解析)
文档属性
| 名称 | 8.3 简单几何体的表面积与体积(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 408.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 00:00:00 | ||
图片预览



文档简介
8.3 简单几何体的表面积与体积
一、单选题
1.在四面体 中, , , ,则它的外接球的面积 ( )
A. B. C. D.
2.底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,底面菱形的对角线的长分别是 和 ,则这个棱柱的侧面积是( )
A.130 B.140 C.150 D.160
3.“正三角形的内切圆半径等于此正三角形的高的 ”,拓展到空间,类比平面几何的上述结论,则正四面体的内切球半径等于这个正四面体的高的( )
A. B. C. D.
4.某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为( ).
A. B. C. D.
5.我国古代数学名著《九章算术》中给出了很多立体几何的结论,其中提到的多面体“鳖臑”是四个面都是直角三角形的三棱锥.若一个“鳖臑”的所有顶点都在球的球面上,且该“鳖臑”的高为,底面是腰长为的等腰直角三角形.则球的表面积为( )
A.12π B. C.6π D.
6.《九章算术》卷第五《商功》中,有“贾令刍童,上广一尺,袤二尺,下广三尺,袤四尺,高一尺。”,意思是:“假设一个刍童,上底面宽1尺,长2尺;下底面宽3尺,长4尺,高1尺(如图)。”(注:刍童为上下底面为相互平行的不相似长方形,两底面的中心连线与底面垂直的几何体),若该几何体所有顶点在一球体的表面上,则该球体的表面积为( )
A. 平方尺 B. 平方尺 C. 平方尺 D. 平方尺
7.如图,在四棱锥 中, ,底面 是边长为 的正方形,点 是 的中点,过点 , 作棱锥的截面,分别与侧棱 , 交于M,N两点,则四棱锥 体积的最小值为( )
A. B. C. D.
8.已知某三棱锥的底面是正三角形,侧棱长均相等,正视图如图所示.若该三棱锥的所有顶点都在球O的球面上,则球O的表面积为( )
A. B. C. D.
二、多选题
9.在正方体中,点E为线段上的动点,则( )
A.直线DE与直线AC所成角为定值
B.点E到直线AB的距离为定值
C.三棱锥的体积为定值
D.三棱锥外接球的体积为定值
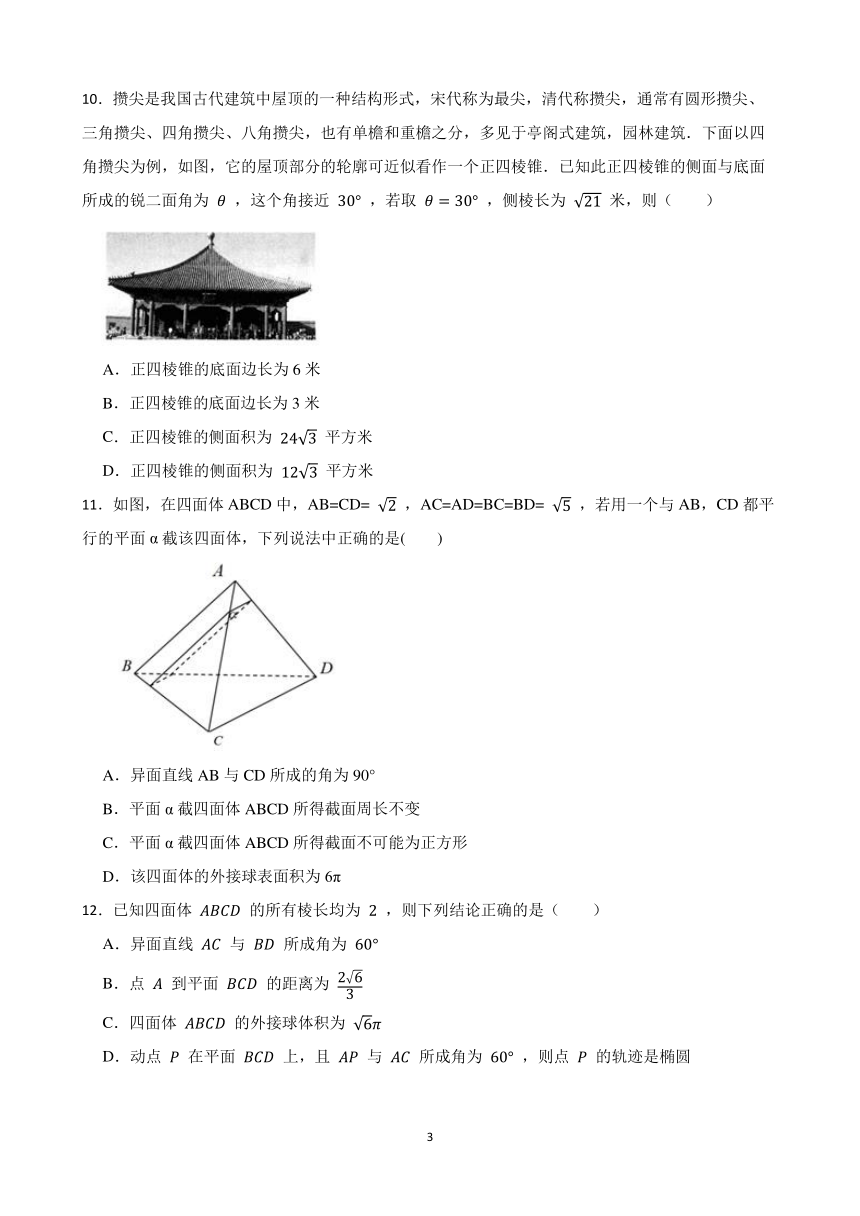
10.攒尖是我国古代建筑中屋顶的一种结构形式,宋代称为最尖,清代称攒尖,通常有圆形攒尖、三角攒尖、四角攒尖、八角攒尖,也有单檐和重檐之分,多见于亭阁式建筑,园林建筑.下面以四角攒尖为例,如图,它的屋顶部分的轮廓可近似看作一个正四棱锥.已知此正四棱锥的侧面与底面所成的锐二面角为 ,这个角接近 ,若取 ,侧棱长为 米,则( )
A.正四棱锥的底面边长为6米
B.正四棱锥的底面边长为3米
C.正四棱锥的侧面积为 平方米
D.正四棱锥的侧面积为 平方米
11.如图,在四面体ABCD中,AB=CD= ,AC=AD=BC=BD= ,若用一个与AB,CD都平行的平面α截该四面体,下列说法中正确的是( )
A.异面直线AB与CD所成的角为90°
B.平面α截四面体ABCD所得截面周长不变
C.平面α截四面体ABCD所得截面不可能为正方形
D.该四面体的外接球表面积为6π
12.已知四面体 的所有棱长均为 ,则下列结论正确的是( )
A.异面直线 与 所成角为
B.点 到平面 的距离为
C.四面体 的外接球体积为
D.动点 在平面 上,且 与 所成角为 ,则点 的轨迹是椭圆
三、填空题
13.张衡(78年~139年)是中国东汉时期杰出的天文学家、数学家、发明家、地理学家、文学家,他的数学著作有《算罔论》.张衡给立方体定名为质,给球体定名为浑.他研究过球的外切立方体体积和内接立方体体积,研究过球的体积,其中还定圆周率值为10的开平方,直到五百多年后,印度和阿拉伯的数学家才得出这个数值.现有棱长为 的正方体,利用张衡的结论可得该正方体的内切球的体积为 .
14.有一个倒圆锥形的容器,其底面半径是5厘米,高是10厘米,容器内放着49个半径为1厘米的玻璃球,在向容器倒满水后,再把玻璃球全部拿出来,则此时容器内水面的高度为 厘米
15.如下图,正方体 棱长为 , 分别为 的中点,则 在底面 上投影的面积是 ;四棱锥 的体积是 .
16.在直三棱柱 中, ,底面三边长分别为3,5,7,P是上底面 所在平面内的动点,若三棱锥 的外接球表面积为 ,则满足题意的动点 的轨迹对应图形的面积为 .
四、解答题
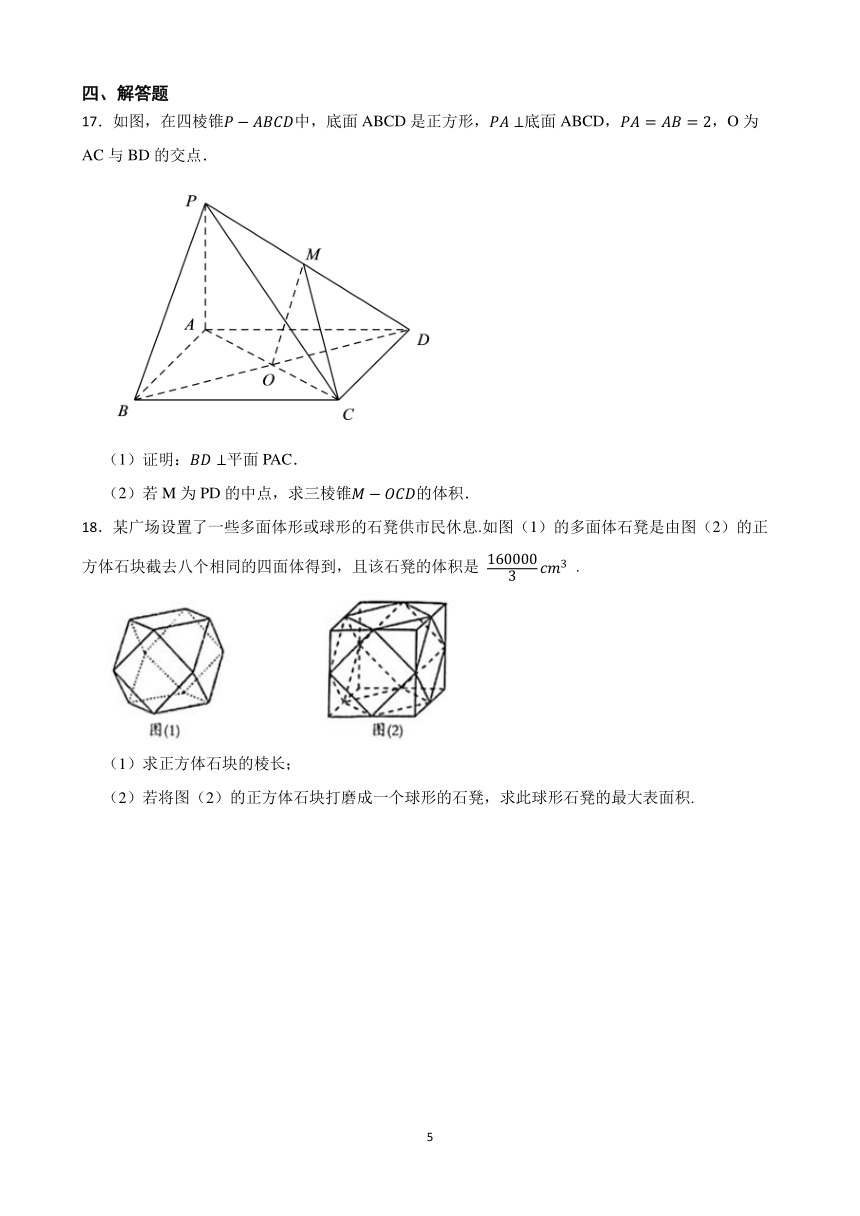
17.如图,在四棱锥中,底面ABCD是正方形,底面ABCD,,O为AC与BD的交点.
(1)证明:平面PAC.
(2)若M为PD的中点,求三棱锥的体积.
18.某广场设置了一些多面体形或球形的石凳供市民休息.如图(1)的多面体石凳是由图(2)的正方体石块截去八个相同的四面体得到,且该石凳的体积是 .
(1)求正方体石块的棱长;
(2)若将图(2)的正方体石块打磨成一个球形的石凳,求此球形石凳的最大表面积.
19.如图所示,在四棱锥 中,四边形 为矩形, 为等腰三角形, ,平面 平面 ,且 , , , 分别为 , 的中点.
(1)证明: 平面 ;
(2)证明:平面 平面 ;
(3)求四棱锥 的体积.
20.如图,在四棱锥 中, ,且 90°.
(1)求证: ;
(2)若 ,四棱锥 的体积为9,求四棱锥 的侧面积
21.如图,在四棱柱中,平面,底面是正方形,且,
(1)求证:平面
(2)求四棱锥的体积.
22.如图,边长为2的正方形ABCD中,
(1)点E是AB的中点,点F是BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.求证:A′D⊥EF
(2)当BE=BF= BC时,求三棱锥A′﹣EFD的体积.
答案解析部分
1.【答案】B
【解析】【解答】由题意 ,
可知 和 是以 为公共边的等腰直角三角形,
取 的中点,则 ,
所以外接球的半径为 ,
所以外接球的表面积为 ,
故答案为:B.
【分析】利用勾股定理,得出Δ B A D 和 Δ B C D 是以 B D 为公共边的等腰直角三角形,取 B D 的中点O,可求外接球的半径,利用球的表面积公式得出外接球的表面积。
2.【答案】D
【解析】【解答】解:由题意可设棱柱底面边长为a,侧棱为h,因为底面是菱形,所以其对角线互相垂直,则,所以棱柱的侧面积为S=4ah=160.
故答案选:D.
【分析】先由菱形的几何特征利用勾股定理求得边长a,再结合题意求出侧面积即可.
3.【答案】C
【解析】【解答】从平面图形类比空间图形,从二维类比三维,可得如下结论:
正四面体的内切球半径等于这个正四面体高的 .
证明如下:球心到正四面体一个面的距离即球的半径 ,连接球心与正四面体的四个顶点.
把正四面体分成四个高为 的三棱锥,所以 ,则 .
(其中 为正四面体一个面的面积, 为正四面体的高)
故答案为:C.
【分析】根据类比推理即可求出结果,再由等体积法验证即可。
4.【答案】D
【解析】【解答】由题意可得,三棱柱的上下底面为边长为2的等边三角形,侧面为三个边长为2的正方形,
则其表面积为: .
故答案为:D.
【分析】首先确定几何体的结构特征,然后求解其表面积即可.
5.【答案】A
【解析】【解答】如下图所示:
在三棱锥中,平面,且,,
因为平面,、、平面,则,,,
,,平面,平面,,
所以,三棱锥的四个面都是直角三角形,且,
,
设线段的中点为,则,
所以,点为三棱锥的外接球球心,
设球的半径为,则,因此,球的表面积为.
故答案为:A.
【分析】 由题意画出图形,可知AD为三棱锥外接球的直径,求解三角形得其长,得到三棱锥外接球半径,则可求出球的表面积 .
6.【答案】B
【解析】【解答】由已知得球心在几何体的外部,
设球心到几何体下底面的距离为x,
则R2=x2+( )2=(x+1)2+( )2,
解得x=2,
∴R2 ,∴该球体的表面积S=41π.
故答案为:B.
【分析】由已知得球心在几何体的外部,设球心到几何体下底面的距离为x,利用勾股定理列式,解得x=2,即可求出该球体的表面积.
7.【答案】D
【解析】【解答】如图所示,设 ,则 ,设三棱锥 的高为 ,三棱锥 的高为 ,
由题得 ,
所以
由题得 ,
因为 平面 ,
所以 ,所以 ,所以 .
在△ 中,由正弦定理得 ,
在△ 中,由正弦定理得 ,
所以
在△ 中, .
所以 ,
当 时, 取最小值 ,所以 取最小值 .
故答案为:D.
【分析】如图所示,设 ,则 ,设三棱锥 的高为 ,三棱锥 的高为 ,先求出 ,再求出 ,求出 的最大值即得解.
8.【答案】A
【解析】【解答】如下图所示,延长 交球O于点 ,设 的外心为点E,连接 , ,
由正弦定理得 ,所以 ,
因为 平面 ,由勾股定理可知,三棱锥 的高 ,所以 ,
由于点A是以 为直径的球O上一点, 所以 ,由射影定理可知,球O的直径 ,
因此,球O的表面积为 .
故答案为:A.
【分析】由正视图和已知条件作出图形如下图所示,利用正弦定理求得 ,再由勾股定理和直角三角形的射影定理求得球的直径,运用球的表面积公式可得选项.
9.【答案】A,C
【解析】【解答】如图所示:
A.因为,又,所以平面,又平面平面,,则直线DE与直线AC所成角为定值,故正确;
B. 当点E与重合时,点E到直线AB的距离,当点E与重合时,点E到直线AB的距离,故错误;
C.因为三棱锥,且点到面EBD的距离为定值, 为定值,故体积为定值,故正确;
D. 易知 平面,所以三棱锥外接球的球心O在上,当点E移动时,球心O的位置改变,则球的半径R改变,所以外接球体积不为定值,故错误;
故答案为:AC
【分析】根据题意由正方体的几何性质以及线面垂直的性质定理,得出线线垂直结合异面直线所成角的定义,即可判断出选项A正确;由点到直线距离的定义以及线面垂直的判定定理即可判断出选项B错误;由等体积法,代入数值计算出结果由此判断出选项C正确;由球以及内接多面体的几何性质,即可得出结论由此判断出选项D错误从而得出答案。
10.【答案】A,C
【解析】【解答】如图,在正四棱锥 中,
O为正方形 的中心, 为 的中点,
则 ,
设底面边长为 .
因为 ,
所以 .
在 中, ,
所以 ,底面边长为6米,
平方米.
故答案为:AC.
【分析】根据题意作出直观图,结合已知条件求解棱锥的底面边长,侧面积,判断选项的正误即可.
11.【答案】A,B,D
【解析】【解答】A.取CD中点M,△ABC为等腰三角形,那么CD⊥AM,
同理,CD⊥BM,且AM∩BM=M,那么CD⊥平面ABM,
而AB 平面ABM,所以CD⊥AB,A正确;
B.如图,设平面a与四面体ABCD的各棱的交点分别为E,F,G,H ,由AB∥平面a,且AB 平面ABD,两个平面的交线为HG,则AB∥HG,同理,FG∥CD,
①, ②
①+②得:HG+HE= ,∴周长为2 ,B正确;
C. E,F,G,H为棱中点时,截面为正方形,C错误;
D.如图,四面体的外接球为正方体的外接球,r= ,故S=6π,D正确
故答案为:ABD.
【分析】根据直线与平面垂直的判定定理与性质定理,结合异面直线所成角的定义可判断A;
根据直线与平面平行的判定定理与性质定理,结合平行直线的性质定理可判断B;
根据四面体的几何特征,结合直线与平面平行的性质定理可判断C;
根据四面体与正方体的几何特征,结合外接球的几何特征可判断D.
12.【答案】B,C
【解析】【解答】取 中点 ,连接 ,可得 面 ,则 ,A不符合题意;
在四面体 中,过点 作 面 于点 ,则 为为底面正三角形 的重心,因为所有棱长均为 , ,即点 到平面 的距离为 ,B符合题意;
设 为正四面体的中心则 为内切球的半径, 我外接球的半径,
因为 ,所以 ,即 ,
所以四面体 的外接球体积 ,C符合题意;
建系如图: ,设 ,则
因为 ,所以 ,
即 ,平方化简可得: ,可知点 的轨迹为双曲线,D不符合题意.
故答案为:BC.
【分析】 由题意画出图形,证明AC⊥BD,可知A错误;直接求出A到底面的距离判断B;求出正四面体外接球的半径,进一步求得外接球的体积判断C;由圆锥曲线的定义判断D.
13.【答案】3600
【解析】【解答】设正方体的棱长为a,内切球的半径为r,
则a=2r,
因为a= ,
所以 ,又 ,
所以球的体积为 ,
故答案为:3600。
【分析】设正方体的棱长为a,内切球的半径为r,再利用正方体与内切球的位置关系,从而推出a=2r,因为a= ,所以 ,又 ,再利用球的体积公式,进而利用张衡的结论可得该正方体的内切球的体积。
14.【答案】6
【解析】【解答】解:设在向容器倒满水后,再把玻璃球全部拿出来,则此时容器内水面的高度为 ,
则 ,
解得 .
故答案为:6.
【分析】设水面的高度为h,根据圆锥体的体积等于全部玻璃的体积加上水的体积列方程求解即可.
15.【答案】2;1
【解析】【解答】
详解:点E在地面的投影为CD中点,
故 在底面 上投影的面积为:
易知 平面 ,点F到平面 的距离为
四棱锥 的体积为:
故答案为:2,1
【分析】找出 Δ A E F 在底面 A B C D 上投影为三角形,利用三角形的面积公式可得结论;利用四棱锥的体积公式即可求解。
16.【答案】
【解析】【解答】不妨设 , , ,
设 为 外接圆圆心,作 平面 ,交平面 于点 ,由三棱锥外接球的性质可知,球心 为 上一点.
设三棱锥 外接球半径为 ,
三棱锥 外接球表面积 , .
在 中,由余弦定理得: ,
,由正弦定理得: ,
,即 , ,
,
即点 的轨迹对应的图形是以 为圆心, 为半径的圆,
对应的图形面积为 .
故答案为: .
【分析】设 为 外接圆圆心,作 平面 ,根据三棱锥外接球的性质可知球心O为 上一点;在 中,结合正余弦定理可求得 的外接圆半径,进而勾股定理可求得球心到平面 的距离,再利用勾股定理求得 ,可得P点轨迹为圆,进而求得结果.
17.【答案】(1)证明:∵底面ABCD,∴.
∵底面ABCD是正方形,∴.
∵平面PAC.,
∴平面PAC.
(2)解:∵O为AC与BD的交点,∴O为AC与BD的中点,
∴.
∵M为PD的中点,∴点M到平面OCD的距离为.
∴
【解析】【分析】(1)根据题意由线面垂直的性质定理即可得出线线垂直,然后再由线面垂直的判定定理即可得证出结论。
(2)利用三角形的面积公式结合中点的性质即可求出边的大小,然后把结果代入到体积公式计算出答案即可。
18.【答案】(1)解:设正方体石块的棱长为 ,
则每个截去的四面体的体积为 .
由题意可得 ,解得 .
故正方体石块的棱长为 ;
(2)解:当球形石凳的面与正方体的各个面都相切时球形石凳的表面积最大.
此时正方体的棱长正好是球的直径,
球形石凳的表面积 .
【解析】【分析】 (1)设正方体石块的棱长为a,求出每个截去的四面体的体积,再由等体积法列式求解a值;
(2)当球形石凳的面与正方体的各个面都相切时球形石凳的表面积最大,可得正方体的棱长正好是球的直径,再由球的表面积公式求解.
19.【答案】(1)解:如图所示,连接 .
∵四边形 为矩形且 是 的中点,
∴ 也是 的中点.
又 是 的中点, ,
∵ 平面 , 平面 ,∴ 平面 .
(2)证明:∵面 平面 , ,平面 平面 ,
∴ 平面 ,
∵ 平面 ,∴平面 平面 .
(3)解:取 的中点为 ,连接 ,
∵平面 平面 , 为等腰直角三角形,
∴ 平面 ,即 为四棱锥 的高,
∵ ,∴ ,又 ,
∴四棱锥 的体积 .
【解析【分析】
【解析】(1)首先根据题意作出辅助线结合中点的性质得出线线平行,再由线面平行的判定定理即可得出结论。
(2)首先由面面垂直的性质定理得到线面垂直 平面 ,在由线面垂直的判定定理即可得出结论。
(3)根据题意取中点作出辅助线,由此得到面面垂直结合等腰三角形的性质即可得出 平面 ,由此得出线线垂直即 为四棱锥 的高 ,结合三角形的计算关系即可求出,再把数值代入到四棱锥的体积公式计算出结果即可。
20.【答案】(1)证明:
又
(2)设 ,则 .
过 作 , 为垂足,
为 中点.
.
.
.
四棱锥P-ABCD的侧面积为:
,
【解析】【分析】(1)首先根据题意得出 ,进而得出 ,再根据面面垂直的判定即证。
(2)根据题意设 , 过 作 , 为垂足,进而得出
, ,根据四棱锥的体积得出a的值,再利用侧面积公式得出 四棱锥P-ABCD的侧面积 。
21.【答案】(1)证明:∵在四棱柱ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是正方形,
∴AC⊥BD,AC⊥DD1,
∵BD∩DD1=D,
∴AC⊥平面BB1D1D.
(2)解:∵D1D⊥平面ABCD,底面ABCD是正方形,
且AB=1,D1D= ,
∴四棱锥D1-ABCD的体积V= = =
22.【答案】(1)解:由正方形ABCD知,∠DCF=∠DAE=90°,
∴A'D⊥A'F,A'D⊥A'E,
∵A'E∩A'F=A',A'E、A'F 平面A'EF.
∴A'D⊥平面A'EF.
又∵EF 平面A'EF,
∴A'D⊥EF.
(2)解:由四边形ABCD为边长为2的正方形
故折叠后A′D=2,A′E=A′F= ,EF=
则cos∠EA′F= =
则sin∠EA′F=
故△EA′F的面积S△EA′F= A′E A′F sin∠EA′F=
由(1)中A′D⊥平面A′EF
可得三棱锥A'﹣EFD的体积V= × ×2=
一、单选题
1.在四面体 中, , , ,则它的外接球的面积 ( )
A. B. C. D.
2.底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,底面菱形的对角线的长分别是 和 ,则这个棱柱的侧面积是( )
A.130 B.140 C.150 D.160
3.“正三角形的内切圆半径等于此正三角形的高的 ”,拓展到空间,类比平面几何的上述结论,则正四面体的内切球半径等于这个正四面体的高的( )
A. B. C. D.
4.某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为( ).
A. B. C. D.
5.我国古代数学名著《九章算术》中给出了很多立体几何的结论,其中提到的多面体“鳖臑”是四个面都是直角三角形的三棱锥.若一个“鳖臑”的所有顶点都在球的球面上,且该“鳖臑”的高为,底面是腰长为的等腰直角三角形.则球的表面积为( )
A.12π B. C.6π D.
6.《九章算术》卷第五《商功》中,有“贾令刍童,上广一尺,袤二尺,下广三尺,袤四尺,高一尺。”,意思是:“假设一个刍童,上底面宽1尺,长2尺;下底面宽3尺,长4尺,高1尺(如图)。”(注:刍童为上下底面为相互平行的不相似长方形,两底面的中心连线与底面垂直的几何体),若该几何体所有顶点在一球体的表面上,则该球体的表面积为( )
A. 平方尺 B. 平方尺 C. 平方尺 D. 平方尺
7.如图,在四棱锥 中, ,底面 是边长为 的正方形,点 是 的中点,过点 , 作棱锥的截面,分别与侧棱 , 交于M,N两点,则四棱锥 体积的最小值为( )
A. B. C. D.
8.已知某三棱锥的底面是正三角形,侧棱长均相等,正视图如图所示.若该三棱锥的所有顶点都在球O的球面上,则球O的表面积为( )
A. B. C. D.
二、多选题
9.在正方体中,点E为线段上的动点,则( )
A.直线DE与直线AC所成角为定值
B.点E到直线AB的距离为定值
C.三棱锥的体积为定值
D.三棱锥外接球的体积为定值
10.攒尖是我国古代建筑中屋顶的一种结构形式,宋代称为最尖,清代称攒尖,通常有圆形攒尖、三角攒尖、四角攒尖、八角攒尖,也有单檐和重檐之分,多见于亭阁式建筑,园林建筑.下面以四角攒尖为例,如图,它的屋顶部分的轮廓可近似看作一个正四棱锥.已知此正四棱锥的侧面与底面所成的锐二面角为 ,这个角接近 ,若取 ,侧棱长为 米,则( )
A.正四棱锥的底面边长为6米
B.正四棱锥的底面边长为3米
C.正四棱锥的侧面积为 平方米
D.正四棱锥的侧面积为 平方米
11.如图,在四面体ABCD中,AB=CD= ,AC=AD=BC=BD= ,若用一个与AB,CD都平行的平面α截该四面体,下列说法中正确的是( )
A.异面直线AB与CD所成的角为90°
B.平面α截四面体ABCD所得截面周长不变
C.平面α截四面体ABCD所得截面不可能为正方形
D.该四面体的外接球表面积为6π
12.已知四面体 的所有棱长均为 ,则下列结论正确的是( )
A.异面直线 与 所成角为
B.点 到平面 的距离为
C.四面体 的外接球体积为
D.动点 在平面 上,且 与 所成角为 ,则点 的轨迹是椭圆
三、填空题
13.张衡(78年~139年)是中国东汉时期杰出的天文学家、数学家、发明家、地理学家、文学家,他的数学著作有《算罔论》.张衡给立方体定名为质,给球体定名为浑.他研究过球的外切立方体体积和内接立方体体积,研究过球的体积,其中还定圆周率值为10的开平方,直到五百多年后,印度和阿拉伯的数学家才得出这个数值.现有棱长为 的正方体,利用张衡的结论可得该正方体的内切球的体积为 .
14.有一个倒圆锥形的容器,其底面半径是5厘米,高是10厘米,容器内放着49个半径为1厘米的玻璃球,在向容器倒满水后,再把玻璃球全部拿出来,则此时容器内水面的高度为 厘米
15.如下图,正方体 棱长为 , 分别为 的中点,则 在底面 上投影的面积是 ;四棱锥 的体积是 .
16.在直三棱柱 中, ,底面三边长分别为3,5,7,P是上底面 所在平面内的动点,若三棱锥 的外接球表面积为 ,则满足题意的动点 的轨迹对应图形的面积为 .
四、解答题
17.如图,在四棱锥中,底面ABCD是正方形,底面ABCD,,O为AC与BD的交点.
(1)证明:平面PAC.
(2)若M为PD的中点,求三棱锥的体积.
18.某广场设置了一些多面体形或球形的石凳供市民休息.如图(1)的多面体石凳是由图(2)的正方体石块截去八个相同的四面体得到,且该石凳的体积是 .
(1)求正方体石块的棱长;
(2)若将图(2)的正方体石块打磨成一个球形的石凳,求此球形石凳的最大表面积.
19.如图所示,在四棱锥 中,四边形 为矩形, 为等腰三角形, ,平面 平面 ,且 , , , 分别为 , 的中点.
(1)证明: 平面 ;
(2)证明:平面 平面 ;
(3)求四棱锥 的体积.
20.如图,在四棱锥 中, ,且 90°.
(1)求证: ;
(2)若 ,四棱锥 的体积为9,求四棱锥 的侧面积
21.如图,在四棱柱中,平面,底面是正方形,且,
(1)求证:平面
(2)求四棱锥的体积.
22.如图,边长为2的正方形ABCD中,
(1)点E是AB的中点,点F是BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.求证:A′D⊥EF
(2)当BE=BF= BC时,求三棱锥A′﹣EFD的体积.
答案解析部分
1.【答案】B
【解析】【解答】由题意 ,
可知 和 是以 为公共边的等腰直角三角形,
取 的中点,则 ,
所以外接球的半径为 ,
所以外接球的表面积为 ,
故答案为:B.
【分析】利用勾股定理,得出Δ B A D 和 Δ B C D 是以 B D 为公共边的等腰直角三角形,取 B D 的中点O,可求外接球的半径,利用球的表面积公式得出外接球的表面积。
2.【答案】D
【解析】【解答】解:由题意可设棱柱底面边长为a,侧棱为h,因为底面是菱形,所以其对角线互相垂直,则,所以棱柱的侧面积为S=4ah=160.
故答案选:D.
【分析】先由菱形的几何特征利用勾股定理求得边长a,再结合题意求出侧面积即可.
3.【答案】C
【解析】【解答】从平面图形类比空间图形,从二维类比三维,可得如下结论:
正四面体的内切球半径等于这个正四面体高的 .
证明如下:球心到正四面体一个面的距离即球的半径 ,连接球心与正四面体的四个顶点.
把正四面体分成四个高为 的三棱锥,所以 ,则 .
(其中 为正四面体一个面的面积, 为正四面体的高)
故答案为:C.
【分析】根据类比推理即可求出结果,再由等体积法验证即可。
4.【答案】D
【解析】【解答】由题意可得,三棱柱的上下底面为边长为2的等边三角形,侧面为三个边长为2的正方形,
则其表面积为: .
故答案为:D.
【分析】首先确定几何体的结构特征,然后求解其表面积即可.
5.【答案】A
【解析】【解答】如下图所示:
在三棱锥中,平面,且,,
因为平面,、、平面,则,,,
,,平面,平面,,
所以,三棱锥的四个面都是直角三角形,且,
,
设线段的中点为,则,
所以,点为三棱锥的外接球球心,
设球的半径为,则,因此,球的表面积为.
故答案为:A.
【分析】 由题意画出图形,可知AD为三棱锥外接球的直径,求解三角形得其长,得到三棱锥外接球半径,则可求出球的表面积 .
6.【答案】B
【解析】【解答】由已知得球心在几何体的外部,
设球心到几何体下底面的距离为x,
则R2=x2+( )2=(x+1)2+( )2,
解得x=2,
∴R2 ,∴该球体的表面积S=41π.
故答案为:B.
【分析】由已知得球心在几何体的外部,设球心到几何体下底面的距离为x,利用勾股定理列式,解得x=2,即可求出该球体的表面积.
7.【答案】D
【解析】【解答】如图所示,设 ,则 ,设三棱锥 的高为 ,三棱锥 的高为 ,
由题得 ,
所以
由题得 ,
因为 平面 ,
所以 ,所以 ,所以 .
在△ 中,由正弦定理得 ,
在△ 中,由正弦定理得 ,
所以
在△ 中, .
所以 ,
当 时, 取最小值 ,所以 取最小值 .
故答案为:D.
【分析】如图所示,设 ,则 ,设三棱锥 的高为 ,三棱锥 的高为 ,先求出 ,再求出 ,求出 的最大值即得解.
8.【答案】A
【解析】【解答】如下图所示,延长 交球O于点 ,设 的外心为点E,连接 , ,
由正弦定理得 ,所以 ,
因为 平面 ,由勾股定理可知,三棱锥 的高 ,所以 ,
由于点A是以 为直径的球O上一点, 所以 ,由射影定理可知,球O的直径 ,
因此,球O的表面积为 .
故答案为:A.
【分析】由正视图和已知条件作出图形如下图所示,利用正弦定理求得 ,再由勾股定理和直角三角形的射影定理求得球的直径,运用球的表面积公式可得选项.
9.【答案】A,C
【解析】【解答】如图所示:
A.因为,又,所以平面,又平面平面,,则直线DE与直线AC所成角为定值,故正确;
B. 当点E与重合时,点E到直线AB的距离,当点E与重合时,点E到直线AB的距离,故错误;
C.因为三棱锥,且点到面EBD的距离为定值, 为定值,故体积为定值,故正确;
D. 易知 平面,所以三棱锥外接球的球心O在上,当点E移动时,球心O的位置改变,则球的半径R改变,所以外接球体积不为定值,故错误;
故答案为:AC
【分析】根据题意由正方体的几何性质以及线面垂直的性质定理,得出线线垂直结合异面直线所成角的定义,即可判断出选项A正确;由点到直线距离的定义以及线面垂直的判定定理即可判断出选项B错误;由等体积法,代入数值计算出结果由此判断出选项C正确;由球以及内接多面体的几何性质,即可得出结论由此判断出选项D错误从而得出答案。
10.【答案】A,C
【解析】【解答】如图,在正四棱锥 中,
O为正方形 的中心, 为 的中点,
则 ,
设底面边长为 .
因为 ,
所以 .
在 中, ,
所以 ,底面边长为6米,
平方米.
故答案为:AC.
【分析】根据题意作出直观图,结合已知条件求解棱锥的底面边长,侧面积,判断选项的正误即可.
11.【答案】A,B,D
【解析】【解答】A.取CD中点M,△ABC为等腰三角形,那么CD⊥AM,
同理,CD⊥BM,且AM∩BM=M,那么CD⊥平面ABM,
而AB 平面ABM,所以CD⊥AB,A正确;
B.如图,设平面a与四面体ABCD的各棱的交点分别为E,F,G,H ,由AB∥平面a,且AB 平面ABD,两个平面的交线为HG,则AB∥HG,同理,FG∥CD,
①, ②
①+②得:HG+HE= ,∴周长为2 ,B正确;
C. E,F,G,H为棱中点时,截面为正方形,C错误;
D.如图,四面体的外接球为正方体的外接球,r= ,故S=6π,D正确
故答案为:ABD.
【分析】根据直线与平面垂直的判定定理与性质定理,结合异面直线所成角的定义可判断A;
根据直线与平面平行的判定定理与性质定理,结合平行直线的性质定理可判断B;
根据四面体的几何特征,结合直线与平面平行的性质定理可判断C;
根据四面体与正方体的几何特征,结合外接球的几何特征可判断D.
12.【答案】B,C
【解析】【解答】取 中点 ,连接 ,可得 面 ,则 ,A不符合题意;
在四面体 中,过点 作 面 于点 ,则 为为底面正三角形 的重心,因为所有棱长均为 , ,即点 到平面 的距离为 ,B符合题意;
设 为正四面体的中心则 为内切球的半径, 我外接球的半径,
因为 ,所以 ,即 ,
所以四面体 的外接球体积 ,C符合题意;
建系如图: ,设 ,则
因为 ,所以 ,
即 ,平方化简可得: ,可知点 的轨迹为双曲线,D不符合题意.
故答案为:BC.
【分析】 由题意画出图形,证明AC⊥BD,可知A错误;直接求出A到底面的距离判断B;求出正四面体外接球的半径,进一步求得外接球的体积判断C;由圆锥曲线的定义判断D.
13.【答案】3600
【解析】【解答】设正方体的棱长为a,内切球的半径为r,
则a=2r,
因为a= ,
所以 ,又 ,
所以球的体积为 ,
故答案为:3600。
【分析】设正方体的棱长为a,内切球的半径为r,再利用正方体与内切球的位置关系,从而推出a=2r,因为a= ,所以 ,又 ,再利用球的体积公式,进而利用张衡的结论可得该正方体的内切球的体积。
14.【答案】6
【解析】【解答】解:设在向容器倒满水后,再把玻璃球全部拿出来,则此时容器内水面的高度为 ,
则 ,
解得 .
故答案为:6.
【分析】设水面的高度为h,根据圆锥体的体积等于全部玻璃的体积加上水的体积列方程求解即可.
15.【答案】2;1
【解析】【解答】
详解:点E在地面的投影为CD中点,
故 在底面 上投影的面积为:
易知 平面 ,点F到平面 的距离为
四棱锥 的体积为:
故答案为:2,1
【分析】找出 Δ A E F 在底面 A B C D 上投影为三角形,利用三角形的面积公式可得结论;利用四棱锥的体积公式即可求解。
16.【答案】
【解析】【解答】不妨设 , , ,
设 为 外接圆圆心,作 平面 ,交平面 于点 ,由三棱锥外接球的性质可知,球心 为 上一点.
设三棱锥 外接球半径为 ,
三棱锥 外接球表面积 , .
在 中,由余弦定理得: ,
,由正弦定理得: ,
,即 , ,
,
即点 的轨迹对应的图形是以 为圆心, 为半径的圆,
对应的图形面积为 .
故答案为: .
【分析】设 为 外接圆圆心,作 平面 ,根据三棱锥外接球的性质可知球心O为 上一点;在 中,结合正余弦定理可求得 的外接圆半径,进而勾股定理可求得球心到平面 的距离,再利用勾股定理求得 ,可得P点轨迹为圆,进而求得结果.
17.【答案】(1)证明:∵底面ABCD,∴.
∵底面ABCD是正方形,∴.
∵平面PAC.,
∴平面PAC.
(2)解:∵O为AC与BD的交点,∴O为AC与BD的中点,
∴.
∵M为PD的中点,∴点M到平面OCD的距离为.
∴
【解析】【分析】(1)根据题意由线面垂直的性质定理即可得出线线垂直,然后再由线面垂直的判定定理即可得证出结论。
(2)利用三角形的面积公式结合中点的性质即可求出边的大小,然后把结果代入到体积公式计算出答案即可。
18.【答案】(1)解:设正方体石块的棱长为 ,
则每个截去的四面体的体积为 .
由题意可得 ,解得 .
故正方体石块的棱长为 ;
(2)解:当球形石凳的面与正方体的各个面都相切时球形石凳的表面积最大.
此时正方体的棱长正好是球的直径,
球形石凳的表面积 .
【解析】【分析】 (1)设正方体石块的棱长为a,求出每个截去的四面体的体积,再由等体积法列式求解a值;
(2)当球形石凳的面与正方体的各个面都相切时球形石凳的表面积最大,可得正方体的棱长正好是球的直径,再由球的表面积公式求解.
19.【答案】(1)解:如图所示,连接 .
∵四边形 为矩形且 是 的中点,
∴ 也是 的中点.
又 是 的中点, ,
∵ 平面 , 平面 ,∴ 平面 .
(2)证明:∵面 平面 , ,平面 平面 ,
∴ 平面 ,
∵ 平面 ,∴平面 平面 .
(3)解:取 的中点为 ,连接 ,
∵平面 平面 , 为等腰直角三角形,
∴ 平面 ,即 为四棱锥 的高,
∵ ,∴ ,又 ,
∴四棱锥 的体积 .
【解析【分析】
【解析】(1)首先根据题意作出辅助线结合中点的性质得出线线平行,再由线面平行的判定定理即可得出结论。
(2)首先由面面垂直的性质定理得到线面垂直 平面 ,在由线面垂直的判定定理即可得出结论。
(3)根据题意取中点作出辅助线,由此得到面面垂直结合等腰三角形的性质即可得出 平面 ,由此得出线线垂直即 为四棱锥 的高 ,结合三角形的计算关系即可求出,再把数值代入到四棱锥的体积公式计算出结果即可。
20.【答案】(1)证明:
又
(2)设 ,则 .
过 作 , 为垂足,
为 中点.
.
.
.
四棱锥P-ABCD的侧面积为:
,
【解析】【分析】(1)首先根据题意得出 ,进而得出 ,再根据面面垂直的判定即证。
(2)根据题意设 , 过 作 , 为垂足,进而得出
, ,根据四棱锥的体积得出a的值,再利用侧面积公式得出 四棱锥P-ABCD的侧面积 。
21.【答案】(1)证明:∵在四棱柱ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是正方形,
∴AC⊥BD,AC⊥DD1,
∵BD∩DD1=D,
∴AC⊥平面BB1D1D.
(2)解:∵D1D⊥平面ABCD,底面ABCD是正方形,
且AB=1,D1D= ,
∴四棱锥D1-ABCD的体积V= = =
22.【答案】(1)解:由正方形ABCD知,∠DCF=∠DAE=90°,
∴A'D⊥A'F,A'D⊥A'E,
∵A'E∩A'F=A',A'E、A'F 平面A'EF.
∴A'D⊥平面A'EF.
又∵EF 平面A'EF,
∴A'D⊥EF.
(2)解:由四边形ABCD为边长为2的正方形
故折叠后A′D=2,A′E=A′F= ,EF=
则cos∠EA′F= =
则sin∠EA′F=
故△EA′F的面积S△EA′F= A′E A′F sin∠EA′F=
由(1)中A′D⊥平面A′EF
可得三棱锥A'﹣EFD的体积V= × ×2=
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
