湖南省岳阳市华容县2023-2024学年高一下学期期末考试数学试题(含答案)
文档属性
| 名称 | 湖南省岳阳市华容县2023-2024学年高一下学期期末考试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 356.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 05:44:09 | ||
图片预览



文档简介
华容县2023-2024学年高一下学期期末考试
数学
注意事项:
1、本试卷分选择题和非选择题两部分,共4页。时量120分钟,满分150分。答题前,考生要将自己的姓名、考号填写在答题卡上。
2、回答选择题时,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷和草稿纸上无效。
3、回答非选择题时,用0.5毫米黑色墨水签字笔将答案按题号写在答题卡上。写在本试卷和草稿纸上无效。
4、考试结束时,将答题卡交回。
一、单项选择题(本大题共8小题,每小题5分,满分40分。每小题给出的四个选项中,只有一个选项是符合题目要求的。)
设,,则在复平面内对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
在中,,则等于
A. B. C. D.
中角所对的边为,若,,则角等于
A. B. C. D.
中,已知点为边上一点,若,,则
A. B. C. D.
在跳水比赛中,有8名评委分别给出某选手原始分,在评定该选手的成绩时,从8个原始分中去掉1个最高分和1个最低分(最高分和最低分不相等),得到6个有效分,这6个有效分与8个原始分相比较,下列说法正确的是
A.中位数,平均分,方差均不变
B.中位数,平均分,方差均变小
C.中位数不变,平均分可能不变,方差变小
D.中位数,平均分,方差都发生改变
正方形ABCD的边长等于2,用斜二测画法画出水平放置的正方形ABCD的直观图,则直观图的面积为
A.4 B. C.2 D.
先后抛掷质地均匀的硬币三次,则至少二次正面朝上的概率是
A. B. C. D.
在一个封闭的直三棱柱内有一个体积为V的球,若,,,,则球的体积的最大值为
A. B. C. D.
二、多项选择题(本大题共3小题,每小题6分,共18分。每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分)
下列各组向量中,不能作为基底的是
A., B.,
C., D.,
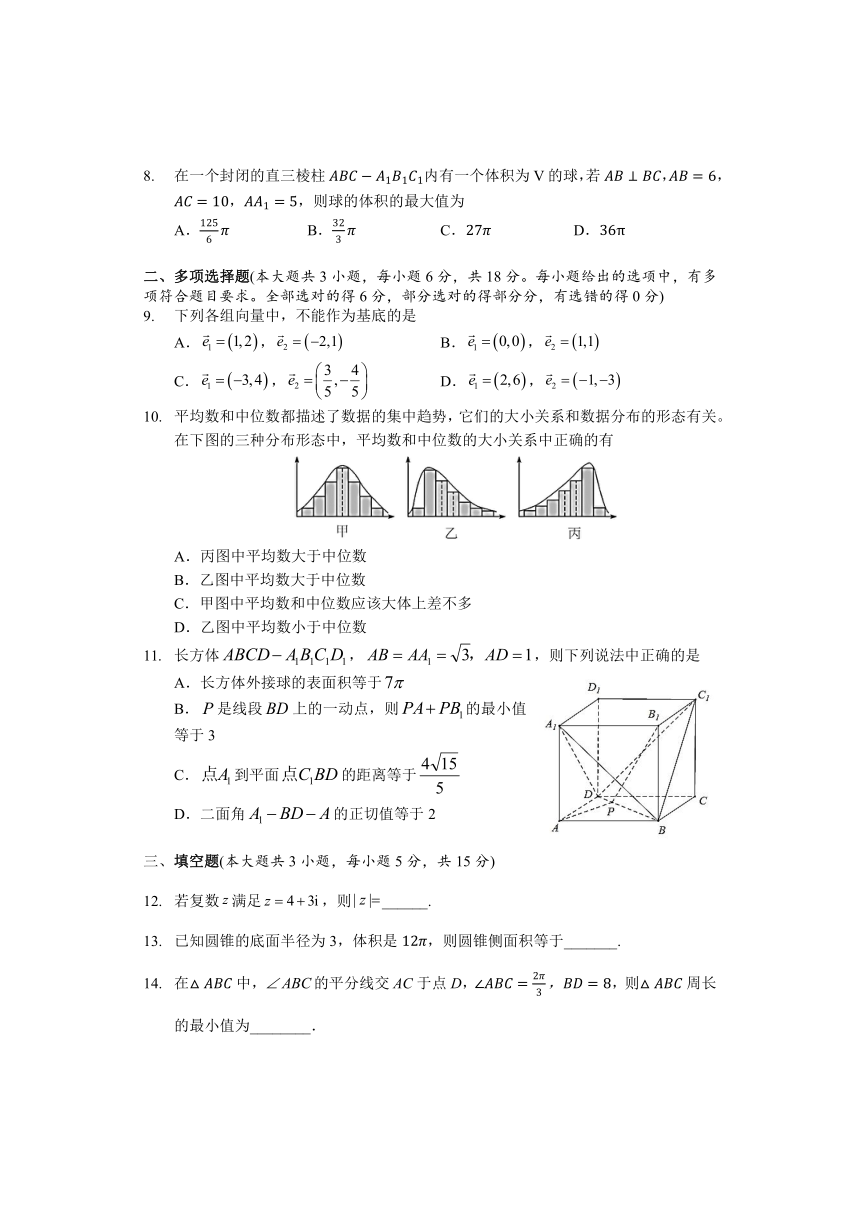
平均数和中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关。在下图的三种分布形态中,平均数和中位数的大小关系中正确的有
A.丙图中平均数大于中位数
B.乙图中平均数大于中位数
C.甲图中平均数和中位数应该大体上差不多
D.乙图中平均数小于中位数
长方体,,则下列说法中正确的是
A.长方体外接球的表面积等于
B.是线段上的一动点,则的最小值等于3
C.到平面的距离等于
D.二面角的正切值等于2
三、填空题(本大题共3小题,每小题5分,共15分)
若复数满足,则______.
已知圆锥的底面半径为3,体积是,则圆锥侧面积等于_______.
在中,的平分线交AC于点D,,则周长的最小值为________.
四、解答题(本大题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤)
(本小题满分13分)
已知向量=(1, 2),=(2, 5),=(2t+1, t) (tR).
(1)若,求t的值;
(2)若与的夹角为钝角,求t的取值范围.
(本小题满分15分)
某校为了增强学生的安全意识,为学生进行了安全知识讲座,讲座后从全校学生中随机抽取了名学生进行笔试试卷满分分,并记录下他们的成绩,将数据分成组:,,,,,并整理得到如下频率分布直方图.
(1)求这部分学生成绩的众数与平均数同组数据用该组区间的中点值作代表;
(2)估计这组数据的上四分位数;
(3)为了更好的了解学生对安全知识的掌握情况,学校决定在成绩高的第、组中用分层抽样的方法抽取名学生,进行第二轮比赛,最终从这名学生中随机抽取人参加市安全知识竞赛,求分包括分以上的同学恰有人被抽到的概率.
(本小题满分15分)
甲、乙、丙三人组成一个小组代表学校参加一个“诗词大会”闯关活动团体赛。三人各自独立闯关,在第一轮比赛中甲闯关成功的概率为,甲、乙都闯关成功的概率为,甲、丙都闯关成功的概率为,每人闯关成功记2分,三人得分之和记为小组团体总分.
(1)求乙、丙各自闯关成功的概率;
(2)求在第一轮比赛中团体总分为4分的概率;
(3)若团体总分不小于4分,则小组可参加下一轮比赛,求该小组参加下一轮比赛的概率.
(本小题满分17分)
如图,四棱锥PABCD,PA平面ABCD,BC//AD,
BAD=90,AB=BC=1,PA=AD=2.点E为PD的中点
(1)求证:CE//平面PAB
(2)求证:CDPAC
(3)求三棱锥PACE的体积
(本小题满分17分)
“费马点”是由十七世纪法国数学家费马提出并征解的一个问题.该问题是:“在一个三角形内求作一点,使其与此三角形的三个顶点的距离之和最小.”意大利数学家托里拆利给出了解答,当ABC的三个内角均小于120时,使得AOB=BOC= COA=120的点O即为费马点;当ABC有一个内角大于或等于120时,最大内角的顶点为费马点.试用以上知识解决下面问题:已知a, b, c分别是ABC三个内角A, B, C的对边,点D在AC上,且AD=2DC,BD=
(1)若= ,
①求B;
②设点P为ABC的费马点,当ABC面积最大时,求++的值;
(2)设点P为ABC的费马点,若cos2B+cos2C-cos2A=1,|PB|+|PC|=t|PA|,求实数t的最小值.
华容县2023-2024学年高一下学期期末考试
数学参考答案及评分标准
一、单项选择题(本大题共8小题,每小题5分,满分40分。每小题给出的四个选项中,只有一个选项是符合题目要求的。)
15.CDCAC 68.DBB
二、多项选择题(本大题共3小题,每小题6分,共18分。每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。)
9.BCD 10.BC 11.ABD
三、填空题(本大题共3小题,每小题5分,共15分)
12.5 13.15 14.
四、解答题(本大题共6小题,满分70分。解答应写出文字说明,证明过程或演算步骤)
17.
15.解:(1)由,可得,…………………………………………2分
所以得,……………………………………5分
…………………………………………6分
(2)因为的夹角为钝角,所以………………………8分
可得,…………………………………………10分
又 当共线时,可得,此时反向,………12分
的取值范围为…………………13分
16.(1)解:众数为最高的小矩形的组中值:,…………………………… 2 分
平均数为:;…… 3 分
根据这组数据计算,可得
………………………………… 7 分
即这组数据的上四分位数为82.5………………………………… 9分
(3)根据等比例分层抽样的方法抽取的名学生,有人,有人,… 11分
设四人编号为,,,,两人编号为,.则所有抽取结果123,124,12a,12b,134,13a,13b,14a,14b,1ab,
234,23a,23b,24a,24b,2ab,34a,34b,3ab,4ab,共个结果,…………… 13分
其中“分包括分以上的同学恰有人”所包含结果共种结果,
所以“分包括分以上的同学恰有人”的概率为,即等于.………………… 15分
解:(1)三人各自独立闯关,其中甲、乙都闯关成功的概率为,甲、丙都闯关成功的概率为,设乙闯关成功的概率为,丙闯关成功的概率为,根据独立事件同时发时的概率公式得,,解得,
即乙闯关成功的概率为,丙闯关成功的概率为……………………………5分
(2)团体总分为4分,即甲、乙、丙三人中恰有2人过关,而另外一人没过关,设“团体总分为4分”为事件A,则,
即团体总分为4分的概率………………10分
团体总分不小于4分,即团体总分为4分或6分,设“团体总分不小于4分”为事件B,由可知团体总分为4分的概率,团体总分为6分,即3人闯关都成功的概率为,所以参加下一轮比赛的概率为,
即该小组参加下一轮比赛的概率为………………………………15分
18.(1)证明:如图,设点F为棱PA的中点,连接EF,BF
则为的中位线,
所以,………………1分
由条件可知,
所以,
所以四边形为平行四边形,……………3分
所以,又,
所以……………5分
(2)证明:由已知条件可求得,
所以,所以,……………7分
又因为,,所以,………9分
又,都含于,
所以。……………11分
(3)解:因为E是PD的中点,所以三棱锥的体积等于三棱锥体积的,
所以……………17分
19. 解:(1)【详解】(1)①因为
由正弦定理可得,…………………………………1分
化简得,因为.…………3分
又,所以………………………4分
②因为,可得,所以,
所以,
又,所以,
可得,由,
所以,当时,面积最大。……………………7分
由三角形内角和性质可知,的三个内角均小于,结合题设易知点一定在的内部.
所以,
所以……………………9分
又因为
.………………………11分
(2)由已知中,
即,
故,由正弦定理可得,
故直角三角形,即,………………………………………12分
点为的费马点,则,
设,,,,
则由得;
由余弦定理得,
,
,
故由得,
即,而,故,
当且仅当,结合,解得时,等号成立,
又,即有,解得或(舍去),
故实数的最小值为.………………………………………………17分
数学
注意事项:
1、本试卷分选择题和非选择题两部分,共4页。时量120分钟,满分150分。答题前,考生要将自己的姓名、考号填写在答题卡上。
2、回答选择题时,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷和草稿纸上无效。
3、回答非选择题时,用0.5毫米黑色墨水签字笔将答案按题号写在答题卡上。写在本试卷和草稿纸上无效。
4、考试结束时,将答题卡交回。
一、单项选择题(本大题共8小题,每小题5分,满分40分。每小题给出的四个选项中,只有一个选项是符合题目要求的。)
设,,则在复平面内对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
在中,,则等于
A. B. C. D.
中角所对的边为,若,,则角等于
A. B. C. D.
中,已知点为边上一点,若,,则
A. B. C. D.
在跳水比赛中,有8名评委分别给出某选手原始分,在评定该选手的成绩时,从8个原始分中去掉1个最高分和1个最低分(最高分和最低分不相等),得到6个有效分,这6个有效分与8个原始分相比较,下列说法正确的是
A.中位数,平均分,方差均不变
B.中位数,平均分,方差均变小
C.中位数不变,平均分可能不变,方差变小
D.中位数,平均分,方差都发生改变
正方形ABCD的边长等于2,用斜二测画法画出水平放置的正方形ABCD的直观图,则直观图的面积为
A.4 B. C.2 D.
先后抛掷质地均匀的硬币三次,则至少二次正面朝上的概率是
A. B. C. D.
在一个封闭的直三棱柱内有一个体积为V的球,若,,,,则球的体积的最大值为
A. B. C. D.
二、多项选择题(本大题共3小题,每小题6分,共18分。每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分)
下列各组向量中,不能作为基底的是
A., B.,
C., D.,
平均数和中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关。在下图的三种分布形态中,平均数和中位数的大小关系中正确的有
A.丙图中平均数大于中位数
B.乙图中平均数大于中位数
C.甲图中平均数和中位数应该大体上差不多
D.乙图中平均数小于中位数
长方体,,则下列说法中正确的是
A.长方体外接球的表面积等于
B.是线段上的一动点,则的最小值等于3
C.到平面的距离等于
D.二面角的正切值等于2
三、填空题(本大题共3小题,每小题5分,共15分)
若复数满足,则______.
已知圆锥的底面半径为3,体积是,则圆锥侧面积等于_______.
在中,的平分线交AC于点D,,则周长的最小值为________.
四、解答题(本大题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤)
(本小题满分13分)
已知向量=(1, 2),=(2, 5),=(2t+1, t) (tR).
(1)若,求t的值;
(2)若与的夹角为钝角,求t的取值范围.
(本小题满分15分)
某校为了增强学生的安全意识,为学生进行了安全知识讲座,讲座后从全校学生中随机抽取了名学生进行笔试试卷满分分,并记录下他们的成绩,将数据分成组:,,,,,并整理得到如下频率分布直方图.
(1)求这部分学生成绩的众数与平均数同组数据用该组区间的中点值作代表;
(2)估计这组数据的上四分位数;
(3)为了更好的了解学生对安全知识的掌握情况,学校决定在成绩高的第、组中用分层抽样的方法抽取名学生,进行第二轮比赛,最终从这名学生中随机抽取人参加市安全知识竞赛,求分包括分以上的同学恰有人被抽到的概率.
(本小题满分15分)
甲、乙、丙三人组成一个小组代表学校参加一个“诗词大会”闯关活动团体赛。三人各自独立闯关,在第一轮比赛中甲闯关成功的概率为,甲、乙都闯关成功的概率为,甲、丙都闯关成功的概率为,每人闯关成功记2分,三人得分之和记为小组团体总分.
(1)求乙、丙各自闯关成功的概率;
(2)求在第一轮比赛中团体总分为4分的概率;
(3)若团体总分不小于4分,则小组可参加下一轮比赛,求该小组参加下一轮比赛的概率.
(本小题满分17分)
如图,四棱锥PABCD,PA平面ABCD,BC//AD,
BAD=90,AB=BC=1,PA=AD=2.点E为PD的中点
(1)求证:CE//平面PAB
(2)求证:CDPAC
(3)求三棱锥PACE的体积
(本小题满分17分)
“费马点”是由十七世纪法国数学家费马提出并征解的一个问题.该问题是:“在一个三角形内求作一点,使其与此三角形的三个顶点的距离之和最小.”意大利数学家托里拆利给出了解答,当ABC的三个内角均小于120时,使得AOB=BOC= COA=120的点O即为费马点;当ABC有一个内角大于或等于120时,最大内角的顶点为费马点.试用以上知识解决下面问题:已知a, b, c分别是ABC三个内角A, B, C的对边,点D在AC上,且AD=2DC,BD=
(1)若= ,
①求B;
②设点P为ABC的费马点,当ABC面积最大时,求++的值;
(2)设点P为ABC的费马点,若cos2B+cos2C-cos2A=1,|PB|+|PC|=t|PA|,求实数t的最小值.
华容县2023-2024学年高一下学期期末考试
数学参考答案及评分标准
一、单项选择题(本大题共8小题,每小题5分,满分40分。每小题给出的四个选项中,只有一个选项是符合题目要求的。)
15.CDCAC 68.DBB
二、多项选择题(本大题共3小题,每小题6分,共18分。每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。)
9.BCD 10.BC 11.ABD
三、填空题(本大题共3小题,每小题5分,共15分)
12.5 13.15 14.
四、解答题(本大题共6小题,满分70分。解答应写出文字说明,证明过程或演算步骤)
17.
15.解:(1)由,可得,…………………………………………2分
所以得,……………………………………5分
…………………………………………6分
(2)因为的夹角为钝角,所以………………………8分
可得,…………………………………………10分
又 当共线时,可得,此时反向,………12分
的取值范围为…………………13分
16.(1)解:众数为最高的小矩形的组中值:,…………………………… 2 分
平均数为:;…… 3 分
根据这组数据计算,可得
………………………………… 7 分
即这组数据的上四分位数为82.5………………………………… 9分
(3)根据等比例分层抽样的方法抽取的名学生,有人,有人,… 11分
设四人编号为,,,,两人编号为,.则所有抽取结果123,124,12a,12b,134,13a,13b,14a,14b,1ab,
234,23a,23b,24a,24b,2ab,34a,34b,3ab,4ab,共个结果,…………… 13分
其中“分包括分以上的同学恰有人”所包含结果共种结果,
所以“分包括分以上的同学恰有人”的概率为,即等于.………………… 15分
解:(1)三人各自独立闯关,其中甲、乙都闯关成功的概率为,甲、丙都闯关成功的概率为,设乙闯关成功的概率为,丙闯关成功的概率为,根据独立事件同时发时的概率公式得,,解得,
即乙闯关成功的概率为,丙闯关成功的概率为……………………………5分
(2)团体总分为4分,即甲、乙、丙三人中恰有2人过关,而另外一人没过关,设“团体总分为4分”为事件A,则,
即团体总分为4分的概率………………10分
团体总分不小于4分,即团体总分为4分或6分,设“团体总分不小于4分”为事件B,由可知团体总分为4分的概率,团体总分为6分,即3人闯关都成功的概率为,所以参加下一轮比赛的概率为,
即该小组参加下一轮比赛的概率为………………………………15分
18.(1)证明:如图,设点F为棱PA的中点,连接EF,BF
则为的中位线,
所以,………………1分
由条件可知,
所以,
所以四边形为平行四边形,……………3分
所以,又,
所以……………5分
(2)证明:由已知条件可求得,
所以,所以,……………7分
又因为,,所以,………9分
又,都含于,
所以。……………11分
(3)解:因为E是PD的中点,所以三棱锥的体积等于三棱锥体积的,
所以……………17分
19. 解:(1)【详解】(1)①因为
由正弦定理可得,…………………………………1分
化简得,因为.…………3分
又,所以………………………4分
②因为,可得,所以,
所以,
又,所以,
可得,由,
所以,当时,面积最大。……………………7分
由三角形内角和性质可知,的三个内角均小于,结合题设易知点一定在的内部.
所以,
所以……………………9分
又因为
.………………………11分
(2)由已知中,
即,
故,由正弦定理可得,
故直角三角形,即,………………………………………12分
点为的费马点,则,
设,,,,
则由得;
由余弦定理得,
,
,
故由得,
即,而,故,
当且仅当,结合,解得时,等号成立,
又,即有,解得或(舍去),
故实数的最小值为.………………………………………………17分
同课章节目录
