北京市燕山地区2023-2024学年七年级下学期期末数学试题(pdf版,含答案)
文档属性
| 名称 | 北京市燕山地区2023-2024学年七年级下学期期末数学试题(pdf版,含答案) |  | |
| 格式 | |||
| 文件大小 | 666.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 09:46:33 | ||
图片预览



文档简介
燕山地区 2023—2024学年度第二学期七年级期末考试
数学试卷
2024年 6月
考生须知
1. 本试卷共 8页,共三道大题,28道小题,满分 100分.考试时间 100分钟.
2. 在试卷和答题纸上准确填写学校名称、班级、姓名和考号.
3. 试题答案一律填涂或书写在答题纸上,在试卷上作答无效.
4. 在答题纸上,选择题、画图题用 2B 铅笔作答,其他试题用黑色字迹签字笔作答.
5. 考试结束,请将试卷和答题纸一并交回.
一、选择题(本题共 20分,每小题 2分)
下面各题均有四个选项,其中只有一个是符合题意的.
1. 2的相反数是( )
A. 2 B. 2 C. 2 D. 1.414
2. “一去二三里,烟村四五家,亭台六七座,八九十枝花.”这首仅 20个字的小诗,数字就占了一半.领悟
到了数学和语文的学科融合.下面四个“数”字的图片中可以通过平移图案(1)得到的是( )
(1)
A. B. C. D.
3. 如图,AB与 CD交于点 O, AOE与 AOC互余, AOE 20 ,则 BOD的度数为( )
A. 20 B. 70 C. 90 D. 110
4. 下列各数中,比大 6且比 7小的数是
A. 28 B. 43 C. 3 64 D. 58
5.一个一元一次不等式的解集在数轴上表示如图所示,则该不等式的解集为( )
A. x 1 B. x C. x 2 D. x 2
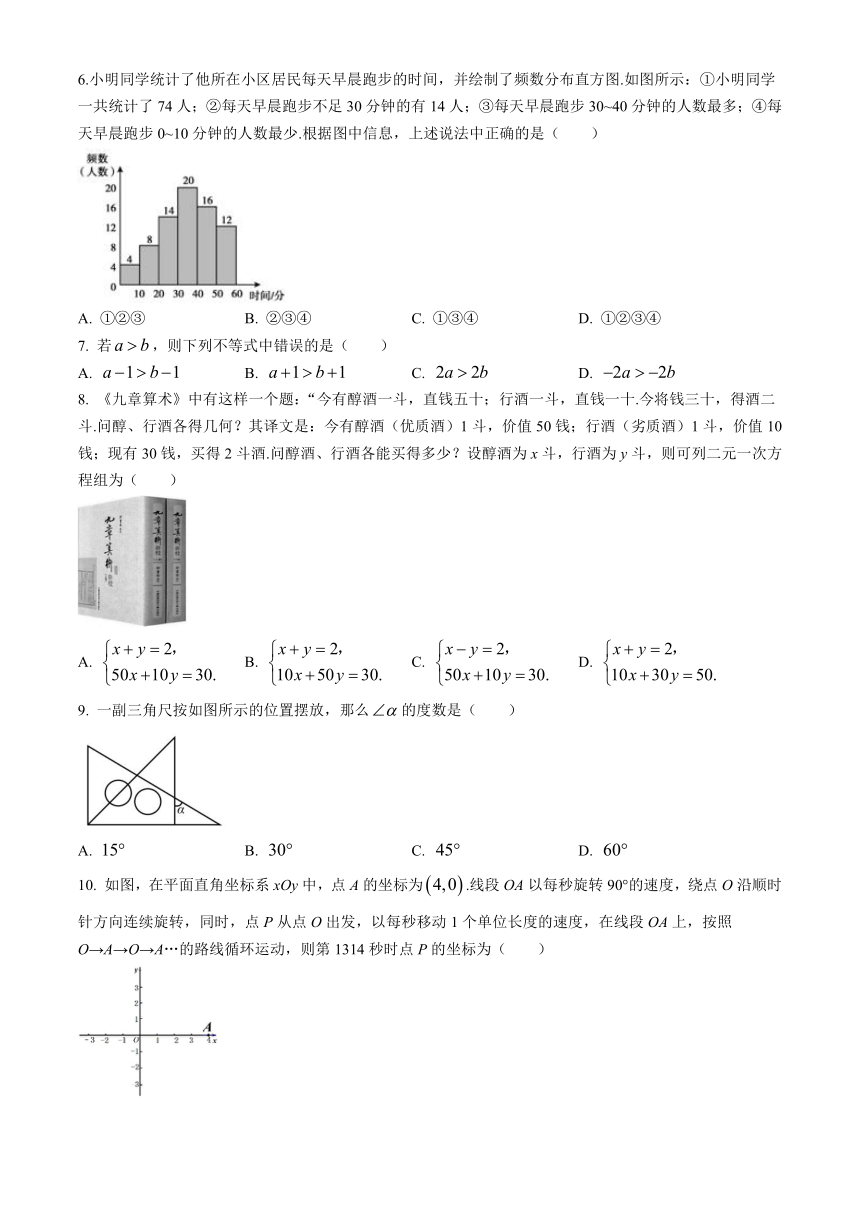
6.小明同学统计了他所在小区居民每天早晨跑步的时间,并绘制了频数分布直方图.如图所示:①小明同学
一共统计了 74人;②每天早晨跑步不足 30分钟的有 14人;③每天早晨跑步 30~40分钟的人数最多;④每
天早晨跑步 0~10分钟的人数最少.根据图中信息,上述说法中正确的是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
7. 若a b,则下列不等式中错误的是( )
A. a 1 b 1 B. a 1 b 1 C. 2a 2b D. 2a 2b
8. 《九章算术》中有这样一个题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二
斗.问醇、行酒各得几何?其译文是:今有醇酒(优质酒)1斗,价值 50钱;行酒(劣质酒)1斗,价值 10
钱;现有 30钱,买得 2斗酒.问醇酒、行酒各能买得多少?设醇酒为 x斗,行酒为 y斗,则可列二元一次方
程组为( )
x y 2, x y 2, x y 2, x y 2,
A. B. C. D.
50x 10y 30.
10x 50y 30.
50x 10y 30.
10x 30y 50.
9. 一副三角尺按如图所示的位置摆放,那么 的度数是( )
A. 15 B. 30 C. 45 D. 60
10. 如图,在平面直角坐标系 xOy中,点 A的坐标为 4,0 .线段 OA以每秒旋转 90°的速度,绕点 O沿顺时
针方向连续旋转,同时,点 P从点 O出发,以每秒移动 1个单位长度的速度,在线段 OA上,按照
O→A→O→A…的路线循环运动,则第 1314秒时点 P的坐标为( )
A. 0,1 B. 0,2 C. 1,0 D. 2,0
二、填空题(本题共 16分,每小题 2分)
16
11. 的平方根是______.
25
12. 如图,把一块含有45 的直角三角形的三角板的两个顶点放在直尺的对边上.如果 1 20 ,那么 2的
度数是______.
13. 已知点P 3, y 到 x轴的距离是 2个单位长度,则 P点的坐标为______.
14. 如图,请你添加一个条件,使 AB∥CD,这个条件是______,你的依据是______.
15. 下列调查,①了解我区饮用水的水质情况,选择抽样调查;②了解某种型号节能灯的使用寿命,选择全
面调查;③了解歼-20新一代双发重型隐形战斗机各零部件的质量,选择抽样调查;④了解一批药品是否合
格,选择全面调查.调查方式选择合理的是______.
16. 一辆匀速行驶的汽车在 11:20距离 A地 50km,要在 12:00之前驶过 A地,道路最高限速 100km/h,该车
速度 v应满足的条件是______.
17. 如图,在平面直角坐标系 xOy中,线段 CB可以看作是线段 AO经过平移得到的,写出一种由线段 AO
得到线段 CB的过程:______.
18. 某段高速公路全长 200千米,交警部门在距离入口 10千米处设置了摄像头,并在以后每隔 18千米处都
设置一个摄像头;此外,交警部门还在高速公路上距离入口 3千米处设立了限速标志牌,并在以后每隔 5
千米处都设置一块限速标志牌(如图).小糖糖坐在后座从入口开始数经过的摄像头和标志牌个数,数到 7
时发现此处同时设置有标志牌和摄像头.小糖糖此时离入口的距离是______千米.
三、解答题(本题共 64分,第 19题 5分,第 20~21题,每题 6分;第 22题 5分,第 23题 6
分,24~27题,每题各 7分,第 28题 8分)
19. 计算: 2 2 3 27—1 2 2 .
5x 17 8(x 1)
20. 解不等式组: x 10 ,并把解集在数轴上表示出来,再写出它的所有正整数x 6 ...
解.
2
x 6y 8,
21. 解方程组:
4x 3y 5.
22. 已知:如图,直线 AB、CD被直线 GH所截, AEG 112 , EFD 68 ,求证: AB∥CD .
完成下面的证明:
证明:∵AB与直线 GH相较于点 E, AEG 112 ,
∴ AEG ______ 112 ,
∵ EFD 68 .
∴ FEB EFD ______.
∴______∥______(____________)(填推理的依据).
23. 按要求画图,并解答问题:
已知:如图,OC平分 AOB,点 D在射线 OA上.
(1)过点 D作直线DE∥OB,交 OC于点 E;
(2)若 AOB 70 ,求 DEC的度数.
24. 如图,在平面直角坐标系 xOy中, A 4,3 ,B 3,1 ,C 1,2 .将三角形 ABC向上平移 3个单位长度,
再向左平移 4个单位长度,可以得到三角形 A1B1C1,其中点 A1、B1、C1分别与点 A、B、C对应.
(1)画出平移后的三角形 A1B1C1;
(2)直接写出 A1、B1、C1三个点的坐标;
(3)已知点 P在 y轴上,以 A1、B1、P为顶点的三角形面积为 2,求点 P的坐标.
25.为了解某小区家庭 4月份用气量情况(该小区共有 300户家庭,每户家庭人数在 2﹣5之间,这 300户
家庭的平均人数约为 3.4).
(1)下面三个样本中,______(填样本序号)的数据能较好地反映该小区家庭 4月份用气量情况;
样本 样本容量 每户家庭人数
样本 1 4 2、3、4、5
样本 2 15 2、2、2、3、3、3、3、3、3、3、3、3、3、3、4
样本 3 15 2、2、3、3、3、3、3、3、3、4、4、4、4、5、5
(2)对样本进行数据整理和描述;
家庭人数 2 2 3 3 3 3 3 3 3 4 4 4 4 5 5
用气量 10 12 13 14 17 17 18 19 20 20 22 26 31 28 31
人均用气量 x 5 6 4.3 4.7 5.7 5.7 6 6.3 6.7 5 5.5 6.5 7.8 5.6 6.2
a.抽样调查小区 15 3户家庭 4月份用气量统计表(单位:m ):
b. 用频数分布表整理数据:
人均用气量分组 4.3 x 5.5 5.5 x 6.7 6.7 x 7.9
频数(家庭数) 4 n 2
c. 用频数分布直方图描述数据:
d. 用扇形统计图描述数据:
根据以上信息,解答下列问题:
①频数分布表整理数据中m ______,补全“频数分布直方图”,扇形统计图描述数据中 n ______;
3
②由样本可以估计出:该小区人均用气量超过6m 的家庭约为:______户;该小区人均用气量在
5.5 x 6.7m3之间的家庭约为______户(结果保留整数).
26. 有 48支队 520名运动员参加篮球、羽毛球比赛,其中每支篮球队 10人,每支羽毛球队 12人,每名运
动员只能参加一项比赛.篮球、羽毛球队各有多少支参赛?
27. 如图,O为直线 AB上一点,OC AB于点 O.点 P为射线 OC上一点,从点 P引两条射线分别交直线
AB于点 D,E(点 D在点 O左侧,点 E在点 O右侧,),过点 O作OF∥PD交 PE于点 F,G为线段 PD
上一点,过 G做GM AB于点 M.
(1)①依题意补全图形;
②若 PDO 27 ,求 POF的度数;
(2)直接写出表示 EOF与 PGM 之间的数量关系的等式.
28. 若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“友好方程”,
x 1 0
例如:方程的3x 6 0解为 x 2 .不等式组 的解集为1 x 4 .因为1 2 4 .所以称方程
x 4
3x 6 0
x 1 0
为不等式组 的“友好方程”.
x 4
2x 3 x 2
(1)请你写出一个方程,使它为不等式组 的“友好方程”;
3(x 1) x 5
3x 1 2x
(2)若关于 x的方程 2x k 4是不等式组 的“友好方程”,求 k的取值范围;
3(x 1) 2(2x 1) 9
x 3m 3m
(3)若关于 x的方程 x 3 4m 0是关于 x的不等式组 的“友好方程”,且此时不等式组
x m 2m 1
有 3个整数解,直接写出 m的取值范围.
燕山地区 2023—2024学年度第二学期七年级期末考试
七年级数学试题参考答案
2024年 6月
一、选择题(本题共 20分,每小题 2分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B B B C C D A D D
二、填空题(本题共 16分,每小题 2分)
11 12 13 14 15 16 17 18
3,2 或 CDA DAB , 线段 AO 向右平移四个单4
25 内错角相等两直线平 ① 75 v 100 位,再向上平移两个单位得 28
5 3, 2 行,(答案不唯一) 到线段 CB.(答案不唯一)
三、解答题(本题共 64分,第 19题 5分,第 20~21题,每题 6分;第 22题 5分,第 23题 6
分,24~27题,每题各 7分,第 28题 8分)
19. 解:原式 2 2 3 1 2 2……3分
2……5分
5x 17 8 x 1 ①
20.
x 6 x 10
.
② 2
解:由①,得 x 3 .……1分
由②,得 x 2 .……2分
∴ 3 x 2 .……3分
∴正整数解为 1,2.……5分
……6分
x 6y 8①
21. 解: .
4x 3y 5②
②×2+①,得9x 18 .……2分
∴ x 2 .……3分
把 x 2代入①,得
2 6y 8 .……4分
y 1……5分
x 2
所以原方程组的解是 .……6分
y 1
22. FEB……1分
180 ……2分
AB……3分
CD……4分
同旁内角互补,两直线平行……5分
23.(1)正确画出DE∥OB,标出点 E;……2分
(2)解:∵OC平分 AOB(已知),
∴ COB 1 AOB(角平分线定义)……3分
2
∵ AOB 70 (已知),
∴ COB 35 (等量代换)……4分
∵DE∥OB(已知),
∴ DEO COB(两直线平行,内错角相等)……5分
∴ DEO 35 (等量代换).
∴ DEC 180 DEO 180 35 145 (补角定义)……6分
24.(1) ……2分
(2) A1 0,6 、 B1 1,4 、C1 3,5 ……5分
(3)∵点 B1到 y轴的距离为 1
1
∴ A
2 1
P 1 2,
∴ A1P 4……6分
∴点 P的坐标为 0,2 或 0,10 ……7分
25.(1)样本 3……1分
(2)①m 9,……2分
补全“频数分布直方图”……4分
n 33.3%;……5分
3 3
②该小区人均用气量超过6m 的家庭约为:100户;该小区人均用气量在5.5 x 6.7m 之间的家庭约为
180户.……7分
26. 解:设有 x支篮球队和 y支羽毛球队参赛.
根据题意,得
x y 48
列方程组 .……4分
10x 12y 520
x 28
解方程组得 .……6分
y 20
答:篮球、羽毛球队分别 28支和 20支参赛.……7分
27.(1)①依题意补全图形……2分
②∵OF∥PD,
∴ 1 2, 3 PDO,……3分
∵ PDO 27 ,∴ 3 27 .
∵OC AB,
∴ 1 3 90 ,……4分
∴ POF 1 63 ……5分
(2) PGM EOF 90 ……7分
28.(1)答案不唯一,方程的解大于 1小于等于 4都可以;……1分
(2)解不等式3x 1 2x得: x 1,
解不等式得:3 x 1 2 2x 1 9, x 4,
3x 1 2x
∴ 的解集为 1 x 4,
3 x 1 2 2x 1 9
1
关于 x的方程 2x k 4的解为 x k 2,……3分
2
3x 1 2x
∵关于 x的方程2x k 4 是不等式组 的“友好方程”,
3 x 1 2 2x 1 9
x 1∴ k 2在 1 x 4范围内,
2
1 1∴ k 2 4,解得 6 k 4;……5分
2
3
(3) m 1……8分
4
数学试卷
2024年 6月
考生须知
1. 本试卷共 8页,共三道大题,28道小题,满分 100分.考试时间 100分钟.
2. 在试卷和答题纸上准确填写学校名称、班级、姓名和考号.
3. 试题答案一律填涂或书写在答题纸上,在试卷上作答无效.
4. 在答题纸上,选择题、画图题用 2B 铅笔作答,其他试题用黑色字迹签字笔作答.
5. 考试结束,请将试卷和答题纸一并交回.
一、选择题(本题共 20分,每小题 2分)
下面各题均有四个选项,其中只有一个是符合题意的.
1. 2的相反数是( )
A. 2 B. 2 C. 2 D. 1.414
2. “一去二三里,烟村四五家,亭台六七座,八九十枝花.”这首仅 20个字的小诗,数字就占了一半.领悟
到了数学和语文的学科融合.下面四个“数”字的图片中可以通过平移图案(1)得到的是( )
(1)
A. B. C. D.
3. 如图,AB与 CD交于点 O, AOE与 AOC互余, AOE 20 ,则 BOD的度数为( )
A. 20 B. 70 C. 90 D. 110
4. 下列各数中,比大 6且比 7小的数是
A. 28 B. 43 C. 3 64 D. 58
5.一个一元一次不等式的解集在数轴上表示如图所示,则该不等式的解集为( )
A. x 1 B. x C. x 2 D. x 2
6.小明同学统计了他所在小区居民每天早晨跑步的时间,并绘制了频数分布直方图.如图所示:①小明同学
一共统计了 74人;②每天早晨跑步不足 30分钟的有 14人;③每天早晨跑步 30~40分钟的人数最多;④每
天早晨跑步 0~10分钟的人数最少.根据图中信息,上述说法中正确的是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
7. 若a b,则下列不等式中错误的是( )
A. a 1 b 1 B. a 1 b 1 C. 2a 2b D. 2a 2b
8. 《九章算术》中有这样一个题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二
斗.问醇、行酒各得几何?其译文是:今有醇酒(优质酒)1斗,价值 50钱;行酒(劣质酒)1斗,价值 10
钱;现有 30钱,买得 2斗酒.问醇酒、行酒各能买得多少?设醇酒为 x斗,行酒为 y斗,则可列二元一次方
程组为( )
x y 2, x y 2, x y 2, x y 2,
A. B. C. D.
50x 10y 30.
10x 50y 30.
50x 10y 30.
10x 30y 50.
9. 一副三角尺按如图所示的位置摆放,那么 的度数是( )
A. 15 B. 30 C. 45 D. 60
10. 如图,在平面直角坐标系 xOy中,点 A的坐标为 4,0 .线段 OA以每秒旋转 90°的速度,绕点 O沿顺时
针方向连续旋转,同时,点 P从点 O出发,以每秒移动 1个单位长度的速度,在线段 OA上,按照
O→A→O→A…的路线循环运动,则第 1314秒时点 P的坐标为( )
A. 0,1 B. 0,2 C. 1,0 D. 2,0
二、填空题(本题共 16分,每小题 2分)
16
11. 的平方根是______.
25
12. 如图,把一块含有45 的直角三角形的三角板的两个顶点放在直尺的对边上.如果 1 20 ,那么 2的
度数是______.
13. 已知点P 3, y 到 x轴的距离是 2个单位长度,则 P点的坐标为______.
14. 如图,请你添加一个条件,使 AB∥CD,这个条件是______,你的依据是______.
15. 下列调查,①了解我区饮用水的水质情况,选择抽样调查;②了解某种型号节能灯的使用寿命,选择全
面调查;③了解歼-20新一代双发重型隐形战斗机各零部件的质量,选择抽样调查;④了解一批药品是否合
格,选择全面调查.调查方式选择合理的是______.
16. 一辆匀速行驶的汽车在 11:20距离 A地 50km,要在 12:00之前驶过 A地,道路最高限速 100km/h,该车
速度 v应满足的条件是______.
17. 如图,在平面直角坐标系 xOy中,线段 CB可以看作是线段 AO经过平移得到的,写出一种由线段 AO
得到线段 CB的过程:______.
18. 某段高速公路全长 200千米,交警部门在距离入口 10千米处设置了摄像头,并在以后每隔 18千米处都
设置一个摄像头;此外,交警部门还在高速公路上距离入口 3千米处设立了限速标志牌,并在以后每隔 5
千米处都设置一块限速标志牌(如图).小糖糖坐在后座从入口开始数经过的摄像头和标志牌个数,数到 7
时发现此处同时设置有标志牌和摄像头.小糖糖此时离入口的距离是______千米.
三、解答题(本题共 64分,第 19题 5分,第 20~21题,每题 6分;第 22题 5分,第 23题 6
分,24~27题,每题各 7分,第 28题 8分)
19. 计算: 2 2 3 27—1 2 2 .
5x 17 8(x 1)
20. 解不等式组: x 10 ,并把解集在数轴上表示出来,再写出它的所有正整数x 6 ...
解.
2
x 6y 8,
21. 解方程组:
4x 3y 5.
22. 已知:如图,直线 AB、CD被直线 GH所截, AEG 112 , EFD 68 ,求证: AB∥CD .
完成下面的证明:
证明:∵AB与直线 GH相较于点 E, AEG 112 ,
∴ AEG ______ 112 ,
∵ EFD 68 .
∴ FEB EFD ______.
∴______∥______(____________)(填推理的依据).
23. 按要求画图,并解答问题:
已知:如图,OC平分 AOB,点 D在射线 OA上.
(1)过点 D作直线DE∥OB,交 OC于点 E;
(2)若 AOB 70 ,求 DEC的度数.
24. 如图,在平面直角坐标系 xOy中, A 4,3 ,B 3,1 ,C 1,2 .将三角形 ABC向上平移 3个单位长度,
再向左平移 4个单位长度,可以得到三角形 A1B1C1,其中点 A1、B1、C1分别与点 A、B、C对应.
(1)画出平移后的三角形 A1B1C1;
(2)直接写出 A1、B1、C1三个点的坐标;
(3)已知点 P在 y轴上,以 A1、B1、P为顶点的三角形面积为 2,求点 P的坐标.
25.为了解某小区家庭 4月份用气量情况(该小区共有 300户家庭,每户家庭人数在 2﹣5之间,这 300户
家庭的平均人数约为 3.4).
(1)下面三个样本中,______(填样本序号)的数据能较好地反映该小区家庭 4月份用气量情况;
样本 样本容量 每户家庭人数
样本 1 4 2、3、4、5
样本 2 15 2、2、2、3、3、3、3、3、3、3、3、3、3、3、4
样本 3 15 2、2、3、3、3、3、3、3、3、4、4、4、4、5、5
(2)对样本进行数据整理和描述;
家庭人数 2 2 3 3 3 3 3 3 3 4 4 4 4 5 5
用气量 10 12 13 14 17 17 18 19 20 20 22 26 31 28 31
人均用气量 x 5 6 4.3 4.7 5.7 5.7 6 6.3 6.7 5 5.5 6.5 7.8 5.6 6.2
a.抽样调查小区 15 3户家庭 4月份用气量统计表(单位:m ):
b. 用频数分布表整理数据:
人均用气量分组 4.3 x 5.5 5.5 x 6.7 6.7 x 7.9
频数(家庭数) 4 n 2
c. 用频数分布直方图描述数据:
d. 用扇形统计图描述数据:
根据以上信息,解答下列问题:
①频数分布表整理数据中m ______,补全“频数分布直方图”,扇形统计图描述数据中 n ______;
3
②由样本可以估计出:该小区人均用气量超过6m 的家庭约为:______户;该小区人均用气量在
5.5 x 6.7m3之间的家庭约为______户(结果保留整数).
26. 有 48支队 520名运动员参加篮球、羽毛球比赛,其中每支篮球队 10人,每支羽毛球队 12人,每名运
动员只能参加一项比赛.篮球、羽毛球队各有多少支参赛?
27. 如图,O为直线 AB上一点,OC AB于点 O.点 P为射线 OC上一点,从点 P引两条射线分别交直线
AB于点 D,E(点 D在点 O左侧,点 E在点 O右侧,),过点 O作OF∥PD交 PE于点 F,G为线段 PD
上一点,过 G做GM AB于点 M.
(1)①依题意补全图形;
②若 PDO 27 ,求 POF的度数;
(2)直接写出表示 EOF与 PGM 之间的数量关系的等式.
28. 若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“友好方程”,
x 1 0
例如:方程的3x 6 0解为 x 2 .不等式组 的解集为1 x 4 .因为1 2 4 .所以称方程
x 4
3x 6 0
x 1 0
为不等式组 的“友好方程”.
x 4
2x 3 x 2
(1)请你写出一个方程,使它为不等式组 的“友好方程”;
3(x 1) x 5
3x 1 2x
(2)若关于 x的方程 2x k 4是不等式组 的“友好方程”,求 k的取值范围;
3(x 1) 2(2x 1) 9
x 3m 3m
(3)若关于 x的方程 x 3 4m 0是关于 x的不等式组 的“友好方程”,且此时不等式组
x m 2m 1
有 3个整数解,直接写出 m的取值范围.
燕山地区 2023—2024学年度第二学期七年级期末考试
七年级数学试题参考答案
2024年 6月
一、选择题(本题共 20分,每小题 2分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B B B C C D A D D
二、填空题(本题共 16分,每小题 2分)
11 12 13 14 15 16 17 18
3,2 或 CDA DAB , 线段 AO 向右平移四个单4
25 内错角相等两直线平 ① 75 v 100 位,再向上平移两个单位得 28
5 3, 2 行,(答案不唯一) 到线段 CB.(答案不唯一)
三、解答题(本题共 64分,第 19题 5分,第 20~21题,每题 6分;第 22题 5分,第 23题 6
分,24~27题,每题各 7分,第 28题 8分)
19. 解:原式 2 2 3 1 2 2……3分
2……5分
5x 17 8 x 1 ①
20.
x 6 x 10
.
② 2
解:由①,得 x 3 .……1分
由②,得 x 2 .……2分
∴ 3 x 2 .……3分
∴正整数解为 1,2.……5分
……6分
x 6y 8①
21. 解: .
4x 3y 5②
②×2+①,得9x 18 .……2分
∴ x 2 .……3分
把 x 2代入①,得
2 6y 8 .……4分
y 1……5分
x 2
所以原方程组的解是 .……6分
y 1
22. FEB……1分
180 ……2分
AB……3分
CD……4分
同旁内角互补,两直线平行……5分
23.(1)正确画出DE∥OB,标出点 E;……2分
(2)解:∵OC平分 AOB(已知),
∴ COB 1 AOB(角平分线定义)……3分
2
∵ AOB 70 (已知),
∴ COB 35 (等量代换)……4分
∵DE∥OB(已知),
∴ DEO COB(两直线平行,内错角相等)……5分
∴ DEO 35 (等量代换).
∴ DEC 180 DEO 180 35 145 (补角定义)……6分
24.(1) ……2分
(2) A1 0,6 、 B1 1,4 、C1 3,5 ……5分
(3)∵点 B1到 y轴的距离为 1
1
∴ A
2 1
P 1 2,
∴ A1P 4……6分
∴点 P的坐标为 0,2 或 0,10 ……7分
25.(1)样本 3……1分
(2)①m 9,……2分
补全“频数分布直方图”……4分
n 33.3%;……5分
3 3
②该小区人均用气量超过6m 的家庭约为:100户;该小区人均用气量在5.5 x 6.7m 之间的家庭约为
180户.……7分
26. 解:设有 x支篮球队和 y支羽毛球队参赛.
根据题意,得
x y 48
列方程组 .……4分
10x 12y 520
x 28
解方程组得 .……6分
y 20
答:篮球、羽毛球队分别 28支和 20支参赛.……7分
27.(1)①依题意补全图形……2分
②∵OF∥PD,
∴ 1 2, 3 PDO,……3分
∵ PDO 27 ,∴ 3 27 .
∵OC AB,
∴ 1 3 90 ,……4分
∴ POF 1 63 ……5分
(2) PGM EOF 90 ……7分
28.(1)答案不唯一,方程的解大于 1小于等于 4都可以;……1分
(2)解不等式3x 1 2x得: x 1,
解不等式得:3 x 1 2 2x 1 9, x 4,
3x 1 2x
∴ 的解集为 1 x 4,
3 x 1 2 2x 1 9
1
关于 x的方程 2x k 4的解为 x k 2,……3分
2
3x 1 2x
∵关于 x的方程2x k 4 是不等式组 的“友好方程”,
3 x 1 2 2x 1 9
x 1∴ k 2在 1 x 4范围内,
2
1 1∴ k 2 4,解得 6 k 4;……5分
2
3
(3) m 1……8分
4
同课章节目录
