2023-2024学年广西南宁三中高一(下)月考数学试卷(三)(含答案)
文档属性
| 名称 | 2023-2024学年广西南宁三中高一(下)月考数学试卷(三)(含答案) | 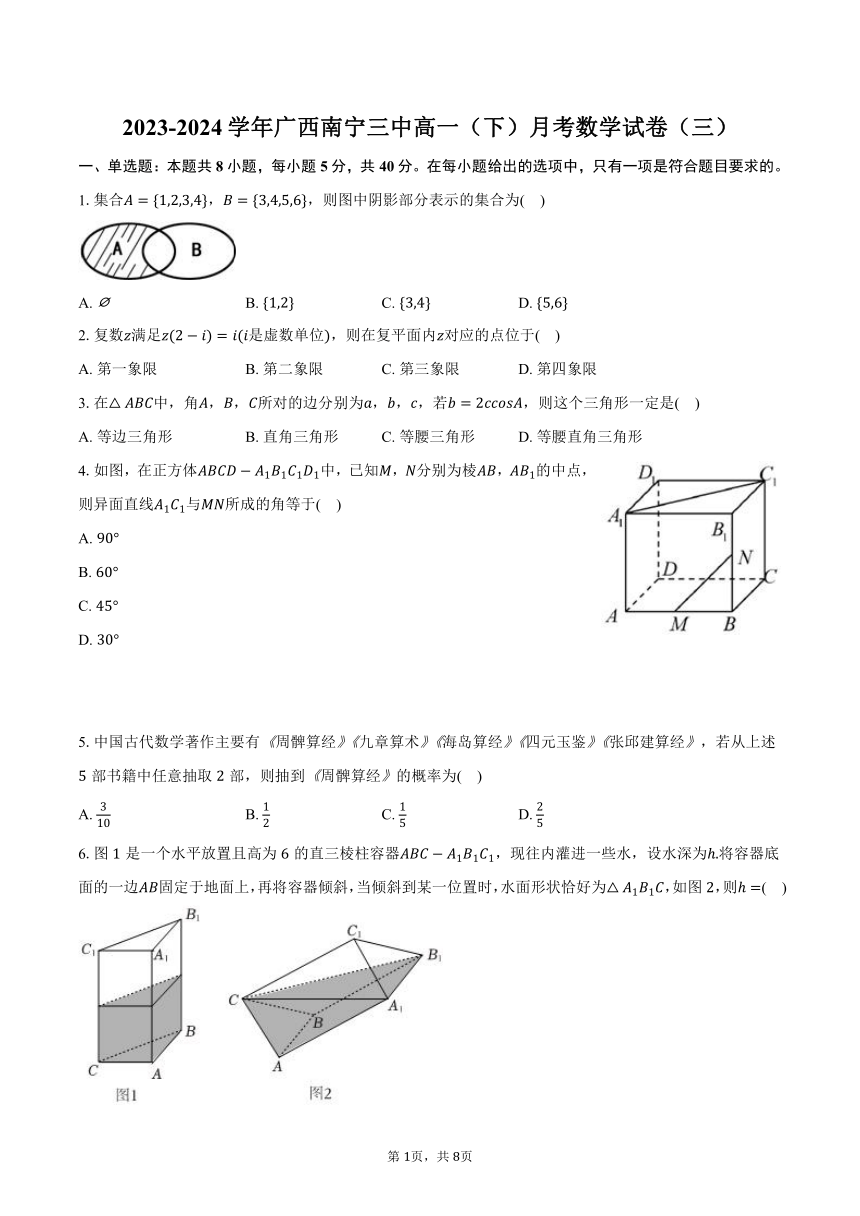 | |
| 格式 | docx | ||
| 文件大小 | 92.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 10:53:38 | ||
图片预览




文档简介
2023-2024学年广西南宁三中高一(下)月考数学试卷(三)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.集合,,则图中阴影部分表示的集合为( )
A. B. C. D.
2.复数满足是虚数单位,则在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3.在中,角,,所对的边分别为,,,若,则这个三角形一定是( )
A. 等边三角形 B. 直角三角形 C. 等腰三角形 D. 等腰直角三角形
4.如图,在正方体中,已知,分别为棱,的中点,则异面直线与所成的角等于( )
A.
B.
C.
D.
5.中国古代数学著作主要有周髀算经九章算术海岛算经四元玉鉴张邱建算经,若从上述部书籍中任意抽取部,则抽到周髀算经的概率为( )
A. B. C. D.
6.图是一个水平放置且高为的直三棱柱容器,现往内灌进一些水,设水深为将容器底面的一边固定于地面上,再将容器倾斜,当倾斜到某一位置时,水面形状恰好为,如图,则( )
A. B. C. D.
7.已知向量,满足,,且对,,则( )
A. B. C. D.
8.如图所示,垂直于以为直径的圆所在的平面,为圆上异于,的任意一点若,,记直线与平面所成的角为,,则的最大值为( )
A.
B.
C.
D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.设,,是三个非零向量,则下列命题正确的有( )
A.
B.
C. 不与垂直
D.
10.设,是两条不同的直线,,是两个不同的平面,下列命题中正确的有( )
A. 若,,,则
B. 若,,,则
C. 若,,,则
D. 若,,,则
11.如图,在直三棱柱中,,,,侧面的对角线交点,点是侧棱上的一个动点,下列结论正确的是( )
A. 直三棱柱的侧面积是
B. 直三棱柱的外接球表面积是
C. 三棱锥的体积与点的位置无关
D. 的最小值为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知向量,,若,则 ______.
13.已知轴截面为正三角形的圆锥的高与球的直径相等,则圆锥的体积与球的体积的比值是______.
14.在平面四边形中,,,,,则四边形的面积为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
如图,在四棱锥中,底面是菱形,平面,为的中点.
Ⅰ求证:平面;
Ⅱ求证:平面.
16.本小题分
已知函数的图象关于直线对称,且图象上相邻个最高点的距离为.
求和的值;
若,求的值.
17.本小题分
本学期初,某校对全校高二学生进行数学测试满分,并从中随机抽取了名学生的成绩,以此为样本,分成,,,,,得到如图所示频率分布直方图.
估计该校高二学生数学成绩的平均数和分位数;
为进一步了解学困生的学习情况,从数学成绩低于分的学生中,分层抽样人,再从人中任取人,求此人分数都在的概率.
18.本小题分
的内角,,的对边分别为,,,已知.
求角的大小;
若,,求的面积;
若角为钝角,直接写出的取值范围.
19.本小题分
如图,在四棱锥中,平面平面,,,,,,.
求点到平面的距离;
求二面角的正切值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.证明:Ⅰ因为底面是菱形,所以,
又因为平面,平面,
所以,而,
可证得:平面;
Ⅱ设,连接,因为底面是菱形,
所以为的中点,为的中点,所以为的中位线,
所以,
又因为平面,平面,
可证得:平面.
16.解:由函数的图象上相邻个最高点的距离为,
可得函数的周期为,求得.
再根据的图象关于直线对称,可得,,
再结合,可得,.
,.
再根据,,.
17.解:由频率直方图得,则,
所以高二数学成绩的平均数为,
前组的频率和为,所以分位数为.
故高二数学平均成绩为,分位数为.
分层抽样人中,的有人,记为,的有人,记为,,,,
从人中任取人,基本事件有,,,,,,,,,,,,,,,共种,
其中人分数都在的有,,,,,共种,
所以从人中任取人,分数都在的概率为.
18.解:由及正弦定理得:
,
因为,
则有,又,,
则,又,故;
由余弦定理,又,,
代入得,由,
可得,即,
故的面积;
由正弦定理,可得,
由,代入化简得:
,
因为钝角,故由,可得,
则,,即,
故的取值范围是.
19.解:平面平面,平面平面,且,即,面,
平面,而平面,
,
又,所以,又,,平面,
平面,,面,
即,,
由面,则,
又,,,
,,
则,故,
,
又平面平面,平面平面,
点到平面的距离即为点到直线的距离,
设点到平面的距离为,则,
设点到平面的距离为,则,
,
即,
解得,
即点到平面的距离为.
如图:
取中点,连结,取中点,连结,,,,
,为中点,所以,
又平面平面,平面平面,面,
平面,又,,
所以,,
由题设易知为正方形,则,且,
且,
则,,,,平面,
平面,平面,
,
在直角三角形中,即为二面角的平面角,
.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.集合,,则图中阴影部分表示的集合为( )
A. B. C. D.
2.复数满足是虚数单位,则在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3.在中,角,,所对的边分别为,,,若,则这个三角形一定是( )
A. 等边三角形 B. 直角三角形 C. 等腰三角形 D. 等腰直角三角形
4.如图,在正方体中,已知,分别为棱,的中点,则异面直线与所成的角等于( )
A.
B.
C.
D.
5.中国古代数学著作主要有周髀算经九章算术海岛算经四元玉鉴张邱建算经,若从上述部书籍中任意抽取部,则抽到周髀算经的概率为( )
A. B. C. D.
6.图是一个水平放置且高为的直三棱柱容器,现往内灌进一些水,设水深为将容器底面的一边固定于地面上,再将容器倾斜,当倾斜到某一位置时,水面形状恰好为,如图,则( )
A. B. C. D.
7.已知向量,满足,,且对,,则( )
A. B. C. D.
8.如图所示,垂直于以为直径的圆所在的平面,为圆上异于,的任意一点若,,记直线与平面所成的角为,,则的最大值为( )
A.
B.
C.
D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.设,,是三个非零向量,则下列命题正确的有( )
A.
B.
C. 不与垂直
D.
10.设,是两条不同的直线,,是两个不同的平面,下列命题中正确的有( )
A. 若,,,则
B. 若,,,则
C. 若,,,则
D. 若,,,则
11.如图,在直三棱柱中,,,,侧面的对角线交点,点是侧棱上的一个动点,下列结论正确的是( )
A. 直三棱柱的侧面积是
B. 直三棱柱的外接球表面积是
C. 三棱锥的体积与点的位置无关
D. 的最小值为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知向量,,若,则 ______.
13.已知轴截面为正三角形的圆锥的高与球的直径相等,则圆锥的体积与球的体积的比值是______.
14.在平面四边形中,,,,,则四边形的面积为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
如图,在四棱锥中,底面是菱形,平面,为的中点.
Ⅰ求证:平面;
Ⅱ求证:平面.
16.本小题分
已知函数的图象关于直线对称,且图象上相邻个最高点的距离为.
求和的值;
若,求的值.
17.本小题分
本学期初,某校对全校高二学生进行数学测试满分,并从中随机抽取了名学生的成绩,以此为样本,分成,,,,,得到如图所示频率分布直方图.
估计该校高二学生数学成绩的平均数和分位数;
为进一步了解学困生的学习情况,从数学成绩低于分的学生中,分层抽样人,再从人中任取人,求此人分数都在的概率.
18.本小题分
的内角,,的对边分别为,,,已知.
求角的大小;
若,,求的面积;
若角为钝角,直接写出的取值范围.
19.本小题分
如图,在四棱锥中,平面平面,,,,,,.
求点到平面的距离;
求二面角的正切值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.证明:Ⅰ因为底面是菱形,所以,
又因为平面,平面,
所以,而,
可证得:平面;
Ⅱ设,连接,因为底面是菱形,
所以为的中点,为的中点,所以为的中位线,
所以,
又因为平面,平面,
可证得:平面.
16.解:由函数的图象上相邻个最高点的距离为,
可得函数的周期为,求得.
再根据的图象关于直线对称,可得,,
再结合,可得,.
,.
再根据,,.
17.解:由频率直方图得,则,
所以高二数学成绩的平均数为,
前组的频率和为,所以分位数为.
故高二数学平均成绩为,分位数为.
分层抽样人中,的有人,记为,的有人,记为,,,,
从人中任取人,基本事件有,,,,,,,,,,,,,,,共种,
其中人分数都在的有,,,,,共种,
所以从人中任取人,分数都在的概率为.
18.解:由及正弦定理得:
,
因为,
则有,又,,
则,又,故;
由余弦定理,又,,
代入得,由,
可得,即,
故的面积;
由正弦定理,可得,
由,代入化简得:
,
因为钝角,故由,可得,
则,,即,
故的取值范围是.
19.解:平面平面,平面平面,且,即,面,
平面,而平面,
,
又,所以,又,,平面,
平面,,面,
即,,
由面,则,
又,,,
,,
则,故,
,
又平面平面,平面平面,
点到平面的距离即为点到直线的距离,
设点到平面的距离为,则,
设点到平面的距离为,则,
,
即,
解得,
即点到平面的距离为.
如图:
取中点,连结,取中点,连结,,,,
,为中点,所以,
又平面平面,平面平面,面,
平面,又,,
所以,,
由题设易知为正方形,则,且,
且,
则,,,,平面,
平面,平面,
,
在直角三角形中,即为二面角的平面角,
.
第1页,共1页
同课章节目录
