2023-2024学年广东省江门市鹤山一中高二(下)第一次段考数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年广东省江门市鹤山一中高二(下)第一次段考数学试卷(含答案) | 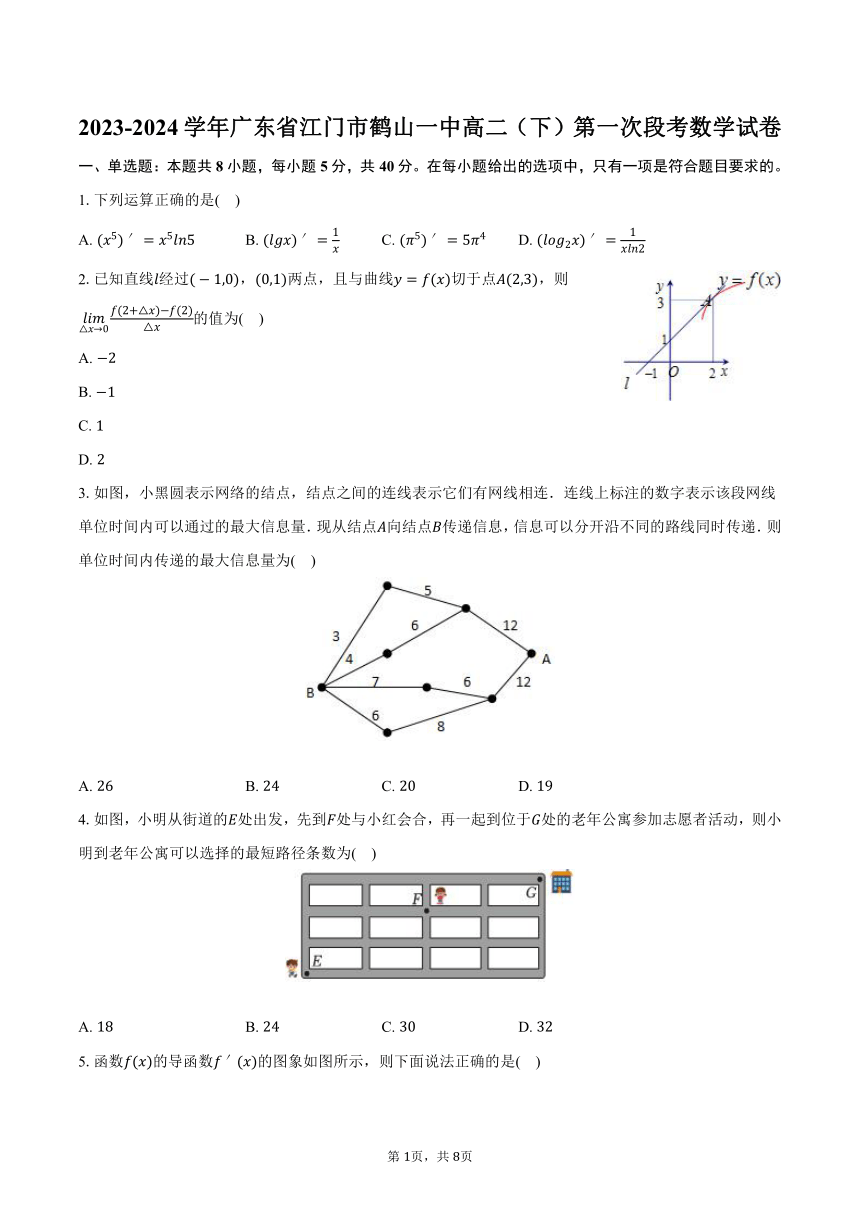 | |
| 格式 | docx | ||
| 文件大小 | 49.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 11:08:35 | ||
图片预览




文档简介
2023-2024学年广东省江门市鹤山一中高二(下)第一次段考数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列运算正确的是( )
A. B. C. D.
2.已知直线经过,两点,且与曲线切于点,则的值为( )
A.
B.
C.
D.
3.如图,小黑圆表示网络的结点,结点之间的连线表示它们有网线相连.连线上标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点向结点传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )
A. B. C. D.
4.如图,小明从街道的处出发,先到处与小红会合,再一起到位于处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )
A. B. C. D.
5.函数的导函数的图象如图所示,则下面说法正确的是( )
A. 为函数的极大值点 B. 函数在区间上单调递增
C. 函数在区间上单调递减 D. 函数在区间上单调递增
6.某高中安排名同学不同姓到甲、乙、丙个小区参加垃圾分类宣传活动,若每名同学只去一个小区,每个小区至少安排名同学,其中张同学不去乙小区,则不同的分配方案种数为( )
A. B. C. D.
7.在数学中,泰勒公式是一个用函数在某点的信息描述其附近取值的公式如果函数足够光滑的话,在已知函数在某一点的各阶导数值的情况之下,泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在一点的邻域中的值,常见的公式有:;则利用泰勒公式估计的近似值为精确到
A. B. C. D.
8.已知定义在上的函数,若函数恰有个零点,则实数的取值范围为( )
A. B.
C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知函数,则( )
A. 为奇函数
B. 的单调递增区间为
C. 的极小值为
D. 若关于的方程恰有个不等的实根,则的取值范围为
10.下列说法正确的是( )
A. 名同学选报跑步、跳高、跳远三个项目,每人报一项,共有种报名方法
B. 从,中选一个数字,从,,中选两个数字,组成无重复数字的三位数,其中奇数的个数为个
C. 名同学争夺跑步、跳高、跳远三项冠军,共有种可能的结果
D. 名同学选报跑步、跳高、跳远三个项目,每项限报一人,且每人至多报一项,共有种报名方法
11.下列说法正确的是( )
A. 若,则
B. 精确到的近似数为
C. 被整除的余数为
D.
三、填空题:本题共3小题,每小题5分,共15分。
12.的展开式的常数项为______.
13.函数在上的单调递减,则实数的取值范围为______.
14.如图,用种不同的颜色对图中个区域涂色种颜色全部使用,要求每个区域涂一种颜色,相邻的区域不能涂相同的颜色,则不同的涂色方法有_______种用数字作答
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知的展开式中,前三项系数的绝对值依次成等差数列.
求展开式中二项式系数最大的项;
求展开式中所有的有理项.
16.本小题分
已知函数,其中.
若在处取得极值,求的值;
当时,讨论的单调性.
17.本小题分
现有男女共个人排成一排照相,其中两个女生相邻的排法种数为多少?
要排一份有个不同的朗诵节目和个不同的说唱节目的节目单,如果说唱节目不排在开头,并且任意两个说唱节目不排在一起,则不同的排法种数为多少?
某医院有内科医生名,其中名女医生,有外科医生名,其中只有名女医生现选派名去甲、乙两地参加赈灾医疗队,要求每队必须名男医生名女医生,且每队由名外科医生名内科医生组成,有多少种派法?最后结果都用数字作答
18.本小题分
记函数的导函数为,的导函数为,设是的定义域的子集,若在区间上,则称在上是“凸函数”已知函数.
Ⅰ若在上为“凸函数”,求的取值范围;
Ⅱ若,判断在区间上的零点个数.
19.本小题分
设是正整数,.
求证:当时,.
求证:当时,.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:展开式中第项为,
所以前三项系数的绝对值依次为,
依题意有,,即,
整理得,解得舍去或.
由二项式系数的性质可知,展开式中第项的二项式系数最大,
即.
由知,,
由可得,,,
故展开式中的有理项为:
,,.
16.解:,
,,
解得.
经过验证.
,
,
时,,
函数在,内单调递增;在内单调递减.
当时,,函数在上单调递增.
当时,,函数在,内单调递增;在内单调递减.
17.解:将两个女生捆绑在一起,当作一个元素,与其他个男生全排列,
则有种排法;
先排个朗诵节目,共种排法,
再排说唱节目,将个说唱节目插入个朗诵节目所形成的个空,
但保证不放到开头,故从剩下个空中选个插空,共有种排法,
所以一共有种排法;
先分类:若外科女医生必选,则一组内科男选,外科男选,
另一组内科女中选女,外科男选,共有种方法,
若外科女医生不选,则一组内科女选,外科男选,
另一组内科女选,外科男选,共有种方法,
由于分赴甲乙两地,所以共有种方法.
18.解:Ⅰ由可得其定义域为,且,
所以,
若在上为“凸函数”可得在恒成立,
当时,显然符合题意;
当时,需满足,可得;
综上可得的取值范围为;
Ⅱ若,可得,所以,
令,则;
易知在区间上恒成立,
因此可得在上单调递减;
显然,
,
根据零点存在定理可得存在使得,
因此可知当时,,即在上为单调递增;
当时,,即在上为单调递减;
又,显然在上不存在零点;
而,结合单调性可得在上存在一个零点;
综上可知,在区间上仅有个零点.
19.证明:记,则只需证.
,由,得:.
所以,在上单调递减,在上单调递增,在上单调递减,
又,,
进而知的最小值.
故,即,
所以当时,.
由,
得.
当时,由知,命题成立;
当时,令,
则.
易知,当时,,当时,,
所以在区间上 函数单调递增,在区间上函数单调递减,
所以当时,取得最大值.
设,,则,
因为,所以,
所以在上单调递减,所以,即,,
所以,得,
于是,
因此,
故当时,,单调递减,
当时,,单调递增,即的最小值为,
所以,即.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列运算正确的是( )
A. B. C. D.
2.已知直线经过,两点,且与曲线切于点,则的值为( )
A.
B.
C.
D.
3.如图,小黑圆表示网络的结点,结点之间的连线表示它们有网线相连.连线上标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点向结点传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )
A. B. C. D.
4.如图,小明从街道的处出发,先到处与小红会合,再一起到位于处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )
A. B. C. D.
5.函数的导函数的图象如图所示,则下面说法正确的是( )
A. 为函数的极大值点 B. 函数在区间上单调递增
C. 函数在区间上单调递减 D. 函数在区间上单调递增
6.某高中安排名同学不同姓到甲、乙、丙个小区参加垃圾分类宣传活动,若每名同学只去一个小区,每个小区至少安排名同学,其中张同学不去乙小区,则不同的分配方案种数为( )
A. B. C. D.
7.在数学中,泰勒公式是一个用函数在某点的信息描述其附近取值的公式如果函数足够光滑的话,在已知函数在某一点的各阶导数值的情况之下,泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在一点的邻域中的值,常见的公式有:;则利用泰勒公式估计的近似值为精确到
A. B. C. D.
8.已知定义在上的函数,若函数恰有个零点,则实数的取值范围为( )
A. B.
C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知函数,则( )
A. 为奇函数
B. 的单调递增区间为
C. 的极小值为
D. 若关于的方程恰有个不等的实根,则的取值范围为
10.下列说法正确的是( )
A. 名同学选报跑步、跳高、跳远三个项目,每人报一项,共有种报名方法
B. 从,中选一个数字,从,,中选两个数字,组成无重复数字的三位数,其中奇数的个数为个
C. 名同学争夺跑步、跳高、跳远三项冠军,共有种可能的结果
D. 名同学选报跑步、跳高、跳远三个项目,每项限报一人,且每人至多报一项,共有种报名方法
11.下列说法正确的是( )
A. 若,则
B. 精确到的近似数为
C. 被整除的余数为
D.
三、填空题:本题共3小题,每小题5分,共15分。
12.的展开式的常数项为______.
13.函数在上的单调递减,则实数的取值范围为______.
14.如图,用种不同的颜色对图中个区域涂色种颜色全部使用,要求每个区域涂一种颜色,相邻的区域不能涂相同的颜色,则不同的涂色方法有_______种用数字作答
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知的展开式中,前三项系数的绝对值依次成等差数列.
求展开式中二项式系数最大的项;
求展开式中所有的有理项.
16.本小题分
已知函数,其中.
若在处取得极值,求的值;
当时,讨论的单调性.
17.本小题分
现有男女共个人排成一排照相,其中两个女生相邻的排法种数为多少?
要排一份有个不同的朗诵节目和个不同的说唱节目的节目单,如果说唱节目不排在开头,并且任意两个说唱节目不排在一起,则不同的排法种数为多少?
某医院有内科医生名,其中名女医生,有外科医生名,其中只有名女医生现选派名去甲、乙两地参加赈灾医疗队,要求每队必须名男医生名女医生,且每队由名外科医生名内科医生组成,有多少种派法?最后结果都用数字作答
18.本小题分
记函数的导函数为,的导函数为,设是的定义域的子集,若在区间上,则称在上是“凸函数”已知函数.
Ⅰ若在上为“凸函数”,求的取值范围;
Ⅱ若,判断在区间上的零点个数.
19.本小题分
设是正整数,.
求证:当时,.
求证:当时,.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:展开式中第项为,
所以前三项系数的绝对值依次为,
依题意有,,即,
整理得,解得舍去或.
由二项式系数的性质可知,展开式中第项的二项式系数最大,
即.
由知,,
由可得,,,
故展开式中的有理项为:
,,.
16.解:,
,,
解得.
经过验证.
,
,
时,,
函数在,内单调递增;在内单调递减.
当时,,函数在上单调递增.
当时,,函数在,内单调递增;在内单调递减.
17.解:将两个女生捆绑在一起,当作一个元素,与其他个男生全排列,
则有种排法;
先排个朗诵节目,共种排法,
再排说唱节目,将个说唱节目插入个朗诵节目所形成的个空,
但保证不放到开头,故从剩下个空中选个插空,共有种排法,
所以一共有种排法;
先分类:若外科女医生必选,则一组内科男选,外科男选,
另一组内科女中选女,外科男选,共有种方法,
若外科女医生不选,则一组内科女选,外科男选,
另一组内科女选,外科男选,共有种方法,
由于分赴甲乙两地,所以共有种方法.
18.解:Ⅰ由可得其定义域为,且,
所以,
若在上为“凸函数”可得在恒成立,
当时,显然符合题意;
当时,需满足,可得;
综上可得的取值范围为;
Ⅱ若,可得,所以,
令,则;
易知在区间上恒成立,
因此可得在上单调递减;
显然,
,
根据零点存在定理可得存在使得,
因此可知当时,,即在上为单调递增;
当时,,即在上为单调递减;
又,显然在上不存在零点;
而,结合单调性可得在上存在一个零点;
综上可知,在区间上仅有个零点.
19.证明:记,则只需证.
,由,得:.
所以,在上单调递减,在上单调递增,在上单调递减,
又,,
进而知的最小值.
故,即,
所以当时,.
由,
得.
当时,由知,命题成立;
当时,令,
则.
易知,当时,,当时,,
所以在区间上 函数单调递增,在区间上函数单调递减,
所以当时,取得最大值.
设,,则,
因为,所以,
所以在上单调递减,所以,即,,
所以,得,
于是,
因此,
故当时,,单调递减,
当时,,单调递增,即的最小值为,
所以,即.
第1页,共1页
同课章节目录
