2024年吉林省中考数学真题(含答案)
文档属性
| 名称 | 2024年吉林省中考数学真题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 887.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 00:00:00 | ||
图片预览


文档简介
2024年吉林省中考数学试卷
一、单项选择题(每小题2分,共12分)
1.若(﹣3)×□的运算结果为正数,则□内的数字可以为( )
A.2 B.1 C.0 D.﹣1
2.长白山天池系由火山口积水成湖,天池湖水碧蓝,水平如镜,群峰倒映,风景秀丽,总蓄水量约达2040000000m3.数据2040000000用科学记数法表示为( )
A.2.04×1010 B.2.04×109
C.20.4×108 D.0.204×1010
3.葫芦在我国古代被看作吉祥之物.如图是一个工艺葫芦的示意图,关于它的三视图说法正确的是( )
A.主视图与左视图相同
B.主视图与俯视图相同
C.左视图与俯视图相同
D.主视图、左视图与俯视图都相同
4.下列方程中,有两个相等实数根的是( )
A.(x﹣2)2=﹣1 B.(x﹣2)2=0 C.(x﹣2)2=1 D.(x﹣2)2=2
5.如图,在平面直角坐标系中,点A的坐标为(﹣4,0),点C的坐标为(0,2).以OA,OC为边作矩形OABC.若将矩形OABC绕点O顺时针旋转90°,得到矩形OA′B′C′,则点B′的坐标为( )
A.(﹣4,﹣2) B.(﹣4,2) C.(2,4) D.(4,2)
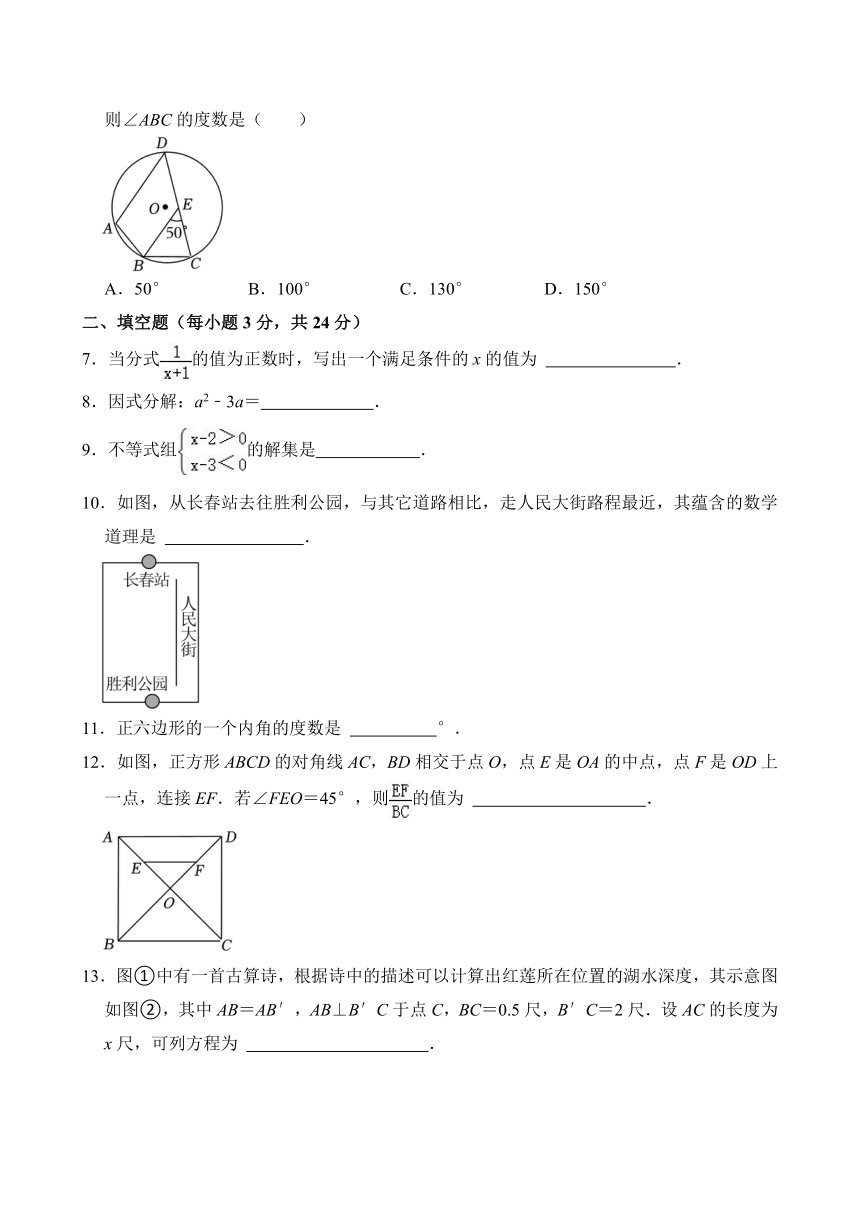
6.如图,四边形ABCD内接于⊙O.过点B作BE∥AD,交CD于点E.若∠BEC=50°,则∠ABC的度数是( )
A.50° B.100° C.130° D.150°
二、填空题(每小题3分,共24分)
7.当分式的值为正数时,写出一个满足条件的x的值为 .
8.因式分解:a2﹣3a= .
9.不等式组的解集是 .
10.如图,从长春站去往胜利公园,与其它道路相比,走人民大街路程最近,其蕴含的数学道理是 .
11.正六边形的一个内角的度数是 °.
12.如图,正方形ABCD的对角线AC,BD相交于点O,点E是OA的中点,点F是OD上一点,连接EF.若∠FEO=45°,则的值为 .
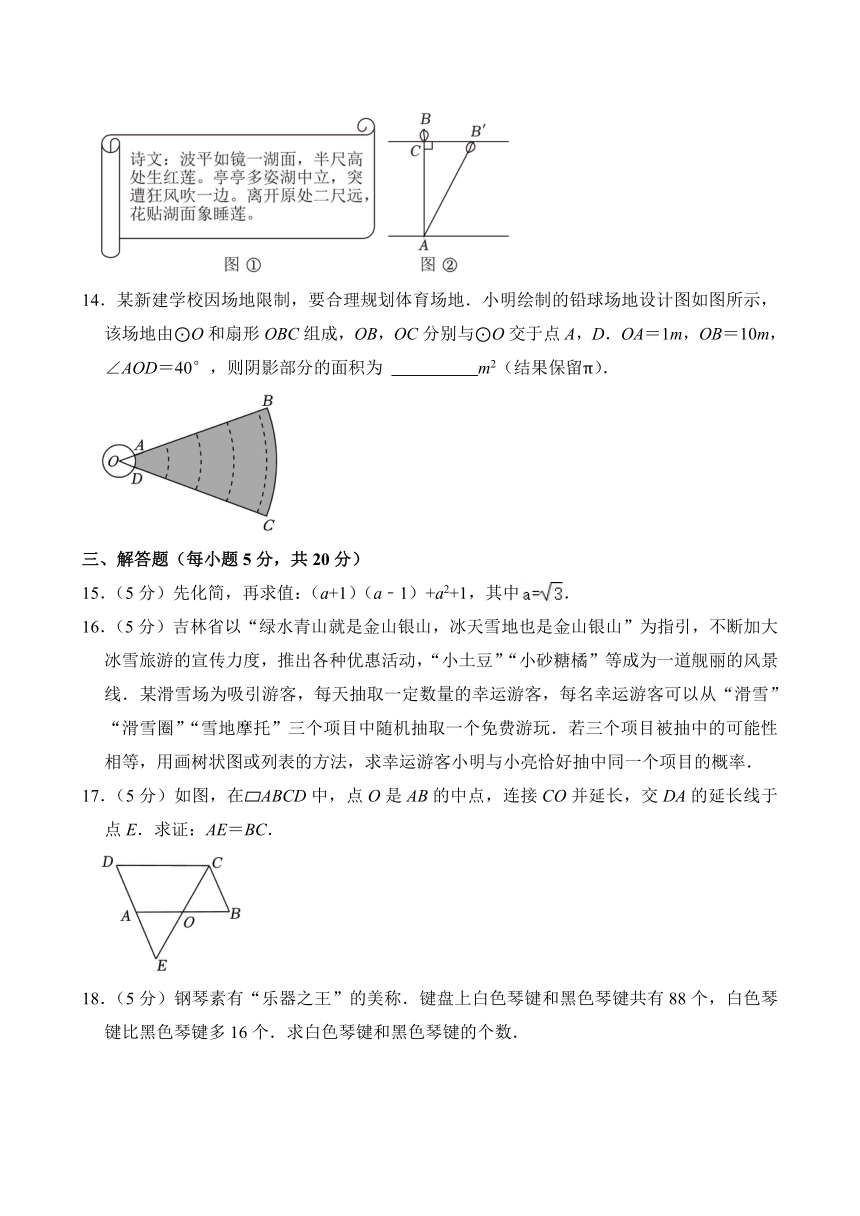
13.图①中有一首古算诗,根据诗中的描述可以计算出红莲所在位置的湖水深度,其示意图如图②,其中AB=AB′,AB⊥B′C于点C,BC=0.5尺,B′C=2尺.设AC的长度为x尺,可列方程为 .
14.某新建学校因场地限制,要合理规划体育场地.小明绘制的铅球场地设计图如图所示,该场地由⊙O和扇形OBC组成,OB,OC分别与⊙O交于点A,D.OA=1m,OB=10m,∠AOD=40°,则阴影部分的面积为 m2(结果保留π).
三、解答题(每小题5分,共20分)
15.(5分)先化简,再求值:(a+1)(a﹣1)+a2+1,其中.
16.(5分)吉林省以“绿水青山就是金山银山,冰天雪地也是金山银山”为指引,不断加大冰雪旅游的宣传力度,推出各种优惠活动,“小土豆”“小砂糖橘”等成为一道舰丽的风景线.某滑雪场为吸引游客,每天抽取一定数量的幸运游客,每名幸运游客可以从“滑雪”“滑雪圈”“雪地摩托”三个项目中随机抽取一个免费游玩.若三个项目被抽中的可能性相等,用画树状图或列表的方法,求幸运游客小明与小亮恰好抽中同一个项目的概率.
17.(5分)如图,在 ABCD中,点O是AB的中点,连接CO并延长,交DA的延长线于点E.求证:AE=BC.
18.(5分)钢琴素有“乐器之王”的美称.键盘上白色琴键和黑色琴键共有88个,白色琴键比黑色琴键多16个.求白色琴键和黑色琴键的个数.
四、解答题(每小题7分,共28分)
19.(7分)图①、图②均是4×4的正方形网格,每个小正方形的顶点称为格点.点A,B,C,D,E,O均在格点上.图①中已画出四边形ABCD,图②中已画出以OE为半径的⊙O.只用无刻度的直尺,在给定的网格中按要求画图.(1)在图①中,画出四边形ABCD的一条对称轴.
(2)在图②中,画出经过点E的⊙O的切线.
20.(7分)已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.
(1)求这个反比例函数的解析式(不要求写出自变量R的取值范围).
(2)当电阻R为3Ω时,求此时的电流I.
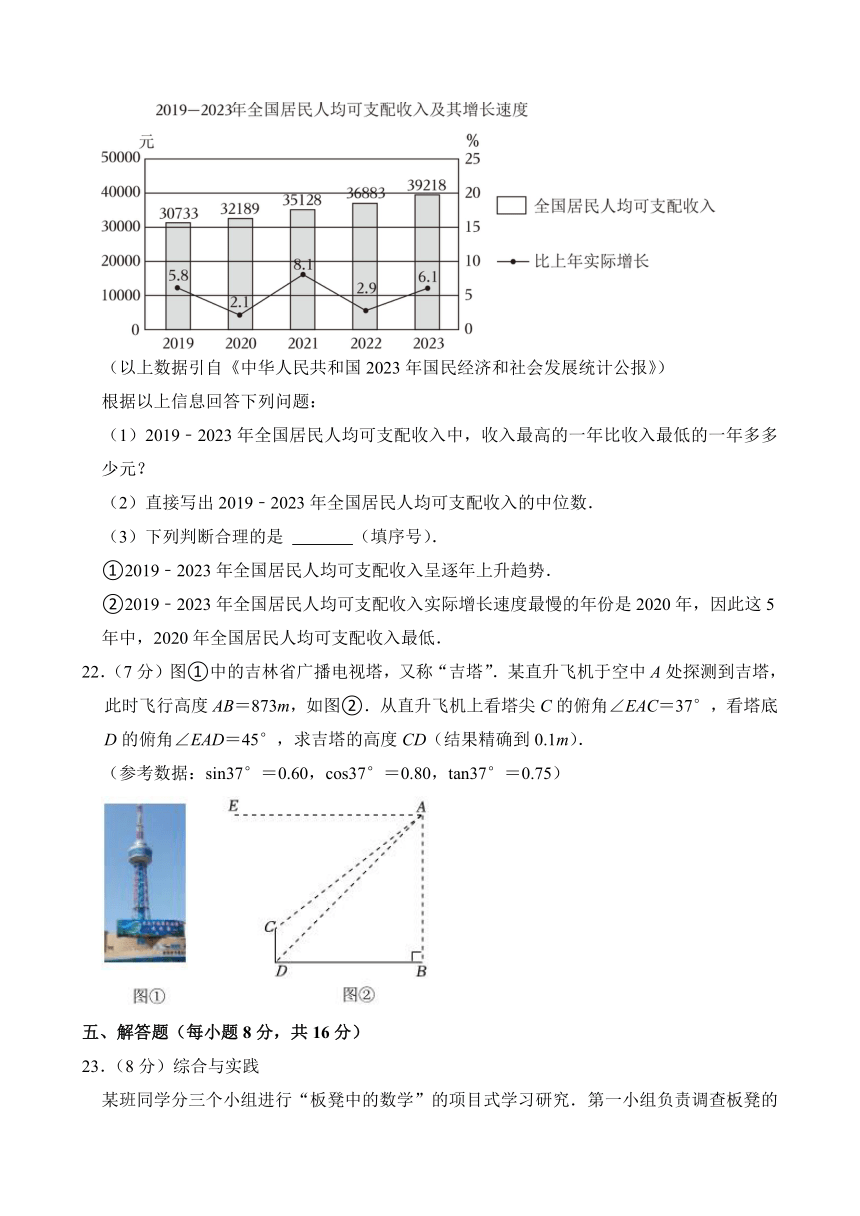
21.(7分)中华人民共和国2019﹣2023年全国居民人均可支配收入及其增长速度情况如图所示.
(以上数据引自《中华人民共和国2023年国民经济和社会发展统计公报》)
根据以上信息回答下列问题:
(1)2019﹣2023年全国居民人均可支配收入中,收入最高的一年比收入最低的一年多多少元?
(2)直接写出2019﹣2023年全国居民人均可支配收入的中位数.
(3)下列判断合理的是 (填序号).
①2019﹣2023年全国居民人均可支配收入呈逐年上升趋势.
②2019﹣2023年全国居民人均可支配收入实际增长速度最慢的年份是2020年,因此这5年中,2020年全国居民人均可支配收入最低.
22.(7分)图①中的吉林省广播电视塔,又称“吉塔”.某直升飞机于空中A处探测到吉塔,此时飞行高度AB=873m,如图②.从直升飞机上看塔尖C的俯角∠EAC=37°,看塔底D的俯角∠EAD=45°,求吉塔的高度CD(结果精确到0.1m).
(参考数据:sin37°=0.60,cos37°=0.80,tan37°=0.75)
五、解答题(每小题8分,共16分)
23.(8分)综合与实践
某班同学分三个小组进行“板凳中的数学”的项目式学习研究.第一小组负责调查板凳的历史及结构特点;第二小组负责研究板凳中蕴含的数学知识;第三小组负责汇报和交流.下面是第三小组汇报的部分内容,请你阅读相关信息,并解答“建立模型”中的问题.
【背景调查】
图①中的板凳又叫“四脚八叉凳”,是中国传统家具,其榫卯结构体现了古人含蓄内敛的审美观.榫眼的设计很有讲究,木工一般用铅笔画出凳面的对称轴,以对称轴为基准向两边各取相同的长度,确定榫眼的位置,如图②所示.板凳的结构设计体现了数学的对称美.
【收集数据】
小组收集了一些板凳并进行了测量.设以对称轴为基准向两边各取相同的长度为x mm,凳面的宽度为y mm,记录如下:
以对称轴为基准向两边各取相同的长度x/mm 16.5 19.8 23.1 26.4 29.7
凳面的宽度y/mm 115.5 132 148.5 165 181.5
【分析数据】
如图③,小组根据表中x,y的数值,在平面直角坐标系中描出了各点.
【建立模型】
请你帮助小组解决下列问题:
(1)观察上述各点的分布规律,它们是否在同一条直线上?如果在同一条直线上,求出这条直线所对应的函数解析式;如果不在同一条直线上,说明理由.
(2)当凳面宽度为213mm时,以对称轴为基准向两边各取相同的长度是多少?
24.(8分)小明在学习时发现四边形面积与对角线存在关联,下面是他的研究过程:
【探究论证】
(1)如图①,在△ABC中,AB=BC,BD⊥AC,垂足为点D.若CD=2,BD=1,则S△ABC= .
(2)如图②,在菱形A′B′C′D′中,A′C′=4,B′D′=2,则S菱形A′B′C′D′= .
(3)如图③,在四边形EFGH中,EG⊥FH,垂足为点O.
若EG=5,FH=3,则S四边形EFGH= ;
若EG=a,FH=b,猜想S四边形EFGH与a,b的关系,并证明你的猜想.
【理解运用】
如图④,在△MNK中,MN=3,KN=4,MK=5,点P为边MN上一点.小明利用直尺和圆规分四步作图;
(ⅰ)以点K为圆心,适当长为半径画弧,分别交边KN,KM于点R,I;
(ⅱ)以点P为圆心,KR长为半径画弧,交线段PM于点I′;
(ⅲ)以点I′为圆心,IR长为半径画弧,交前一条弧于点R′,点R′,K在MN同侧;
(ⅳ)过点P画射线PR′,在射线PR′上截取PQ=KN,连接KP,KQ,MQ.
请你直接写出S四边形MPKQ的值.
六、解答题(每小题10分,共20分)
25.(10分)如图,在△ABC中,∠C=90°,∠B=30°,AC=3cm,AD是△ABC的角平分线.动点P从点A出发,以的速度沿折线AD﹣DB向终点B运动.过点P作PQ∥AB,交AC于点Q,以PQ为边作等边三角形PQE,且点C,E在PQ同侧.设点P的运动时间为t(s)(t>0),△PQE与△ABC重合部分图形的面积为S(cm2).
(1)当点P在线段AD上运动时,判断△APQ的形状(不必证明),并直接写出AQ的长(用含t的代数式表示).
(2)当点E与点C重合时,求t的值.
(3)求S关于t的函数解析式,并写出自变量t的取值范围.
26.(10分)小明利用一次函数和二次函数知识,设计了一个计算程序,其程序框图如图(1)所示,输入x的值为﹣2时,输出y的值为1;输入x的值为2时,输出y的值为3;输入x的值为3时,输出y的值为6.
(1)直接写出k,a,b的值.
(2)小明在平面直角坐标系中画出了关于x的函数图象,如图(2).
Ⅰ.当y随x的增大而增大时,求x的取值范围.
Ⅱ.若关于x的方程ax2+bx+3﹣t=0(t为实数),在0<x<4时无解,求t的取值范围.
Ⅲ.若在函数图象上有点P,Q(P与Q不重合).P的横坐标为m,Q的横坐标为﹣m+1.小明对P,Q之间(含P,Q两点)的图象进行研究,当图象对应函数的最大值与最小值均不随m的变化而变化,直接写出m的取值范围.
参考答案
一、单项选择题(每小题2分,共12分)
1.解:(﹣3)×2=﹣6,故A选项错误;
(﹣3)×1=﹣3,故B选项错误;
(﹣3)×0=0,故C选项错误;
(﹣3)×(﹣1)=3,故D选项正确;
故选:D.
2.解:2040000000=2.04×109.
故选:B.
3.解:这个几何体的主视图与左视图相同,俯视图与主视图和左视图不相同,
故选:A.
4.解:A、(x﹣2)2=﹣1化简为方程x2﹣4x+5=0,
∵a=1,b=﹣4,c=5,
∴Δ=(﹣4)2﹣4×1×5=﹣4<0,
此方程没有实数根,不符合题意;
B、(x﹣2)2=0,化简为x2﹣4x+4=0,
∵a=1,b=﹣4,c=4,
∴Δ=(﹣4)2﹣4×1×4=0,
∴此方程有两个相等实数根,符合题意;
C、(x﹣2)2=1,化简为方程x2﹣4x+3=0中,
∵a=1,b=﹣4,c=3,
∴Δ=(﹣4)2﹣4×1×3=4>0,
∴此方程有两个不相等的实数根,不符合题意;
D、方程(x﹣2)2=2,化简为可化为x2﹣4x+2=0,
∵a=1,b=﹣4,c=2,
∴Δ=42﹣4×1×2=16﹣8=8>0,
∴此方程有两个不相等的实数根,不符合题意.
故选:B.
5.解:∵点A的坐标为(﹣4,0),点C的坐标为(0,2),
∴OA=4,OC=2,
∵四边形ABCO是矩形,
∴BC=OA=4,
∵将矩形OABC绕点O顺时针旋转90°,得到矩形OA′B′C′,
∴OC′=OC=2,B′C′=BC=4,
∴点B′的坐标为(2,4).
故选:C.
6.解:∵BE∥AD,
∴∠ADC=∠BEC=50°,
∵四边形ABCD内接于⊙O,
∴∠ABC=180°﹣∠ADC=130°.
故选:C.
二、填空题(每小题3分,共24分)
7.解:∵>0,1>0,
∴x+1>0,即x>﹣1,
则满足条件x的值可以为0(答案不唯一).
故答案为:0(答案不唯一).
8.解:a2﹣3a=a(a﹣3).
故答案为:a(a﹣3).
9.解:,
由①得:x>2,
由②得:x<3,
∴不等式组的解集是:2<x<3.
故答案为:2<x<3.
10.解:其中蕴含的数学道理是两点之间,线段最短,
故答案为:两点之间,线段最短.
11.解:由题意得:180°×(6﹣2)÷6=120°,
故答案为:120.
12.解:∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°,AD=BC,
∵∠FEO=45°,
∴∠FEO=∠DAC,
∴EF∥AD,
∵点E是OA的中点,
∴点F是OD的中点,
∴EF是△AOD的中位线,
∴EF=AD,
∴EF=BC,
即,
故答案为:.
13.解:在Rt△AB'C中,由勾股定理得,
AC2+B'C2=AB'2,
即x2+22=(x+0.5)2,
故答案为:x2+22=(x+0.5)2.
14.解:阴影部分的面积为:=11π(m2).
故答案为:11π.
三、解答题(每小题5分,共20分)
15.解:(a+1)(a﹣1)+a2+1
=a2﹣1+a2+1
=2a2
∵'
∴原式=2×()2=6.
16.解:把“滑雪”“滑雪圈”“雪地摩托”三个项目分别记为A、B、C,
画树状图如下:
共有9种等可能的结果,其中幸运游客小明与小亮恰好抽中同一个项目的结果有3种,
∴幸运游客小明与小亮恰好抽中同一个项目的概率为=.
17.证明:∵点O是AB的中点,
∴AO=OB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠E=∠BCO,
又∠AOE=∠BOC,
∴△AOE≌△BOC(AAS),
∴AE=BC.
18.解:设白色琴键的个数为x个,黑色琴键的个数为y个,
由题意得:,
解得:,
答:白色琴键的个数为52个,黑色琴键的个数为36个.
四、解答题(每小题7分,共28分)
19.解:(1)如图①所示,直线GH与直线EF即为所求;
(2)如图②所示,直线AB即为所求.
20.解:(1)设I=,
由题意得:K=RI=36,
∴这个反比例函数的解析式为I=;
(2)电阻R为3Ω时,I==12A.
21.解:(1)39218﹣30733=8485(元),
答:2019﹣2023年全国居民人均可支配收入中,收入最高的一年比收入最低多8485元;
(2)把2019﹣2023年全国居民人均可支配收入从小到大排列,排在中间的数是2021年人均可支配收入,
所以2019﹣2023年全国居民人均可支配收入的中位数是35128元;
(3)由折线统计图可知,
2019﹣2023年全国居民人均可支配收入呈逐年上升趋势,故①说法正确;
因为2019﹣2023年全国居民人均可支配收入呈逐年上升趋势,所以这5年中,2019年全国居民人均可支配收入最低,故②说法错误.
故答案为:①.
22.解:过点C作CF⊥AB,垂足为F.
∵AB⊥BD,CF⊥AB,DC⊥BD,
∴∠CDB=∠B=∠CFB=90°.
∴四边形CDBF是矩形.
∴BF=CD,CF=BD=873m.
∵CF∥BD∥AE,
∴∠EAC=∠ACF=37°,∠EAD=∠ADB=45°.
在Rt△ACF中,
∵tan∠ACF=,
∴AF=tan∠ACF CF
=tan37°×873
≈0.75×873
≈654.75(m).
在Rt△DBA中,
∵tan∠ADB=,
∴AB=tan∠ADB BD
=tan45°×873
=1×873
=873(m).
∴CD=FB=AB﹣AF
=873﹣654.75
=218.25
≈218.3(m).
答:吉塔的高度CD约为218.3m.
五、解答题(每小题8分,共16分)
23.解:(1)它们在同一条直线上,
设y=kx+b,
则:,
解得:,
所以这条直线所对应的函数解析式为y=5x+33;
(2)当y=213mm时,213=5x+33,
解得:x=36,
所以当凳面宽度为213mm时,以对称轴为基准向两边各取相同的长度是36mm.
24.解:(1)∵在△ABC中,AB=AC,BD⊥AC,CD=2,
∴AD=CD=2,
∴AC=4,
∴S△ABC=AC BD=2.
故答案为:2.
(2)∵在菱形S菱形A'B'C'D'A'B'C'D'中,A'C'=4,B'D'=2,
∴S菱形A'B'C'D'=A'C' B'D'=4,
故答案为:4.
(3)∵EG⊥FH,
∴S△EFG=EG FO,S△EHG=EG HO,
∴S四边形EFGH=S△EFG+S△EHG=EG FO+EG HO=EG FH=,
故答案为:.
猜想:S四边形EFGH=,
证明:∴S△EFG=EG FO,S△EHG=EG HO,
∴S四边形EFGH=S△EFG+S△EHG=EG FO+EG HO=EG FH=.
(4)根据尺规作图可知:∠QPM=∠MKN,
∵在△MNK中,MN=3,KN=4,MK=5,
∴MK2=MN2+KN2,
∴△MNK是直角三角形,且∠MNK=90°,
∴∠NMK+∠MKN=90°,
∵∠QPM=∠MKN,
∴∠NMK+∠QPM=90°,
∴MK⊥PQ,
∵PQ=KN=4,MK=5,
∴根据(3)中结论得S四边形MPKQ=MK PQ=10.
六、解答题(每小题10分,共20分)
25.解:(1)如图,过Q作QH⊥AD于点H,
∵PQ∥AB,
∴∠BAD=∠QAP,
∵AD是角平分线,
∴∠CAD=∠BAD,
∴∠CAD=∠QAP,
∴QA=QP,
∴△APQ是等腰三角形.
∵QH⊥AP,
∴AH=AP=,
∵∠CAD=30°,
∴AQ==t,
故△APQ是等腰三角形,AQ=t.
(2)如图所示,E、C重合时图形.
∵△PQE是等边三角形,
∴QE=QP,
由(1)得QA=QP,
∴AE=2AQ,即2t=3,
∴t=.
(3)①当点P在AD上,点E在AC上时,重合部分是等边三角形PQE,如图作PG⊥QE于点G,
∵∠PAQ=30°,
∴PG=AP=t,
∵△PQE是等边三角形,
∴QE=PQ=AQ=t,
∴S=QE PG=.
由(2)知当点EC重合时,t=,
∴S=(0<t≤).
②当点P在AD上,点E在AC延长线上时,重合部分时四边形PQCF.
在Rt△FCE中,CE=2t﹣3,∠E=60°,
∴CF=CE tan60°=(2t﹣3),
∴S△PCE=(2t﹣3) (2t﹣3)=(2t﹣3)2,
∴S=S△PAC﹣S△PCE=﹣(2t﹣3)2=﹣t2+6t﹣(<t<2).
③当点P在DB上,重合部分时直角三角形PQC,
S=CQ CP=(t﹣1) (t﹣1)=(t﹣1)2,(2≤t≤4).
综上所述,S=.
26.(1)解:∵x=﹣2<0,
∴将 x=﹣2,y=1 代入 y=kx+3,得:﹣2k+3=1,解得:k=1,
∵x=2>0,x=3>0,
将x=2,y=3和x=3,y=6分别代入 y=ax2+bx+3 得:,
解得:;
故:a=1,b=﹣2,k=1.
(2)解:I:∵k=1,a=1,b=﹣2,
∴一次函数解析式为:y=x+3,二次函数解析式为:y=x2﹣2x+3,
当x>0时,y=x2﹣2x+3,其对称轴为直线x=1,开口向上,
∴x≥1时,y随着x的增大而增大;
当x≤0时,y=x+3,k=1>0,
∴x≤0时,y随着x的增大而增大,
综上,x的取值范围:x≤0或x≥1;
Ⅱ:∵ax2+bx+3﹣t=0在0<x<4时无解,
∴ax2+bx+3=t,在0<x<4时无解,
∴问题转化为抛物线 y=x2﹣2x+3 与直线y=t在0<x<4时无交点,
∵对于 y=x2﹣2x+3,当x=1时,y=2,
∴顶点为(1,2),
如图:
∴当t=2时,抛物线 y=x2﹣2x+3 与直线y=t在0<x<4时正好一个交点,
∴当t<2时,抛物线 y=x2﹣2x+3 与直线y=t在0<x<4时没有交点;
当x=4,y=16﹣8+3=11,
∴当t=11时,抛物线 y=x2﹣2x+3 与直线y=t在0<x≤4时正好一个交点,
∴当t≥11时,抛物线 y=x2﹣2x+3 与直线y=t在0<x<4时没有交点,
∴当t<2或t≥11时,抛物线 y=x2﹣2x+3 与直线y=t在0<x<4时没有交点,
即:当t<2或t≥11时,关于x的方程 ax2+bx+3﹣t=0 (t为实数),在0<x<4时无解;
Ⅲ:∵xP=m,xQ=﹣m+1,
∴,
∴点P、Q关于直线 对称,
当 x=1,y最小值=1﹣2+3=2,
当 x=0时,y最大值=3,
∵当图象对应函数的最大值与最小值均不随m的变化而变化,而当 x=2 时,y=3,x=﹣1 时,y=2,
∴①当 如图:
由题意得:,
∴1≤m≤2;
②当 ,如图:
由题意得:,
∴﹣1≤m≤0,
综上:﹣1≤m≤0或1≤m≤2.
一、单项选择题(每小题2分,共12分)
1.若(﹣3)×□的运算结果为正数,则□内的数字可以为( )
A.2 B.1 C.0 D.﹣1
2.长白山天池系由火山口积水成湖,天池湖水碧蓝,水平如镜,群峰倒映,风景秀丽,总蓄水量约达2040000000m3.数据2040000000用科学记数法表示为( )
A.2.04×1010 B.2.04×109
C.20.4×108 D.0.204×1010
3.葫芦在我国古代被看作吉祥之物.如图是一个工艺葫芦的示意图,关于它的三视图说法正确的是( )
A.主视图与左视图相同
B.主视图与俯视图相同
C.左视图与俯视图相同
D.主视图、左视图与俯视图都相同
4.下列方程中,有两个相等实数根的是( )
A.(x﹣2)2=﹣1 B.(x﹣2)2=0 C.(x﹣2)2=1 D.(x﹣2)2=2
5.如图,在平面直角坐标系中,点A的坐标为(﹣4,0),点C的坐标为(0,2).以OA,OC为边作矩形OABC.若将矩形OABC绕点O顺时针旋转90°,得到矩形OA′B′C′,则点B′的坐标为( )
A.(﹣4,﹣2) B.(﹣4,2) C.(2,4) D.(4,2)
6.如图,四边形ABCD内接于⊙O.过点B作BE∥AD,交CD于点E.若∠BEC=50°,则∠ABC的度数是( )
A.50° B.100° C.130° D.150°
二、填空题(每小题3分,共24分)
7.当分式的值为正数时,写出一个满足条件的x的值为 .
8.因式分解:a2﹣3a= .
9.不等式组的解集是 .
10.如图,从长春站去往胜利公园,与其它道路相比,走人民大街路程最近,其蕴含的数学道理是 .
11.正六边形的一个内角的度数是 °.
12.如图,正方形ABCD的对角线AC,BD相交于点O,点E是OA的中点,点F是OD上一点,连接EF.若∠FEO=45°,则的值为 .
13.图①中有一首古算诗,根据诗中的描述可以计算出红莲所在位置的湖水深度,其示意图如图②,其中AB=AB′,AB⊥B′C于点C,BC=0.5尺,B′C=2尺.设AC的长度为x尺,可列方程为 .
14.某新建学校因场地限制,要合理规划体育场地.小明绘制的铅球场地设计图如图所示,该场地由⊙O和扇形OBC组成,OB,OC分别与⊙O交于点A,D.OA=1m,OB=10m,∠AOD=40°,则阴影部分的面积为 m2(结果保留π).
三、解答题(每小题5分,共20分)
15.(5分)先化简,再求值:(a+1)(a﹣1)+a2+1,其中.
16.(5分)吉林省以“绿水青山就是金山银山,冰天雪地也是金山银山”为指引,不断加大冰雪旅游的宣传力度,推出各种优惠活动,“小土豆”“小砂糖橘”等成为一道舰丽的风景线.某滑雪场为吸引游客,每天抽取一定数量的幸运游客,每名幸运游客可以从“滑雪”“滑雪圈”“雪地摩托”三个项目中随机抽取一个免费游玩.若三个项目被抽中的可能性相等,用画树状图或列表的方法,求幸运游客小明与小亮恰好抽中同一个项目的概率.
17.(5分)如图,在 ABCD中,点O是AB的中点,连接CO并延长,交DA的延长线于点E.求证:AE=BC.
18.(5分)钢琴素有“乐器之王”的美称.键盘上白色琴键和黑色琴键共有88个,白色琴键比黑色琴键多16个.求白色琴键和黑色琴键的个数.
四、解答题(每小题7分,共28分)
19.(7分)图①、图②均是4×4的正方形网格,每个小正方形的顶点称为格点.点A,B,C,D,E,O均在格点上.图①中已画出四边形ABCD,图②中已画出以OE为半径的⊙O.只用无刻度的直尺,在给定的网格中按要求画图.(1)在图①中,画出四边形ABCD的一条对称轴.
(2)在图②中,画出经过点E的⊙O的切线.
20.(7分)已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.
(1)求这个反比例函数的解析式(不要求写出自变量R的取值范围).
(2)当电阻R为3Ω时,求此时的电流I.
21.(7分)中华人民共和国2019﹣2023年全国居民人均可支配收入及其增长速度情况如图所示.
(以上数据引自《中华人民共和国2023年国民经济和社会发展统计公报》)
根据以上信息回答下列问题:
(1)2019﹣2023年全国居民人均可支配收入中,收入最高的一年比收入最低的一年多多少元?
(2)直接写出2019﹣2023年全国居民人均可支配收入的中位数.
(3)下列判断合理的是 (填序号).
①2019﹣2023年全国居民人均可支配收入呈逐年上升趋势.
②2019﹣2023年全国居民人均可支配收入实际增长速度最慢的年份是2020年,因此这5年中,2020年全国居民人均可支配收入最低.
22.(7分)图①中的吉林省广播电视塔,又称“吉塔”.某直升飞机于空中A处探测到吉塔,此时飞行高度AB=873m,如图②.从直升飞机上看塔尖C的俯角∠EAC=37°,看塔底D的俯角∠EAD=45°,求吉塔的高度CD(结果精确到0.1m).
(参考数据:sin37°=0.60,cos37°=0.80,tan37°=0.75)
五、解答题(每小题8分,共16分)
23.(8分)综合与实践
某班同学分三个小组进行“板凳中的数学”的项目式学习研究.第一小组负责调查板凳的历史及结构特点;第二小组负责研究板凳中蕴含的数学知识;第三小组负责汇报和交流.下面是第三小组汇报的部分内容,请你阅读相关信息,并解答“建立模型”中的问题.
【背景调查】
图①中的板凳又叫“四脚八叉凳”,是中国传统家具,其榫卯结构体现了古人含蓄内敛的审美观.榫眼的设计很有讲究,木工一般用铅笔画出凳面的对称轴,以对称轴为基准向两边各取相同的长度,确定榫眼的位置,如图②所示.板凳的结构设计体现了数学的对称美.
【收集数据】
小组收集了一些板凳并进行了测量.设以对称轴为基准向两边各取相同的长度为x mm,凳面的宽度为y mm,记录如下:
以对称轴为基准向两边各取相同的长度x/mm 16.5 19.8 23.1 26.4 29.7
凳面的宽度y/mm 115.5 132 148.5 165 181.5
【分析数据】
如图③,小组根据表中x,y的数值,在平面直角坐标系中描出了各点.
【建立模型】
请你帮助小组解决下列问题:
(1)观察上述各点的分布规律,它们是否在同一条直线上?如果在同一条直线上,求出这条直线所对应的函数解析式;如果不在同一条直线上,说明理由.
(2)当凳面宽度为213mm时,以对称轴为基准向两边各取相同的长度是多少?
24.(8分)小明在学习时发现四边形面积与对角线存在关联,下面是他的研究过程:
【探究论证】
(1)如图①,在△ABC中,AB=BC,BD⊥AC,垂足为点D.若CD=2,BD=1,则S△ABC= .
(2)如图②,在菱形A′B′C′D′中,A′C′=4,B′D′=2,则S菱形A′B′C′D′= .
(3)如图③,在四边形EFGH中,EG⊥FH,垂足为点O.
若EG=5,FH=3,则S四边形EFGH= ;
若EG=a,FH=b,猜想S四边形EFGH与a,b的关系,并证明你的猜想.
【理解运用】
如图④,在△MNK中,MN=3,KN=4,MK=5,点P为边MN上一点.小明利用直尺和圆规分四步作图;
(ⅰ)以点K为圆心,适当长为半径画弧,分别交边KN,KM于点R,I;
(ⅱ)以点P为圆心,KR长为半径画弧,交线段PM于点I′;
(ⅲ)以点I′为圆心,IR长为半径画弧,交前一条弧于点R′,点R′,K在MN同侧;
(ⅳ)过点P画射线PR′,在射线PR′上截取PQ=KN,连接KP,KQ,MQ.
请你直接写出S四边形MPKQ的值.
六、解答题(每小题10分,共20分)
25.(10分)如图,在△ABC中,∠C=90°,∠B=30°,AC=3cm,AD是△ABC的角平分线.动点P从点A出发,以的速度沿折线AD﹣DB向终点B运动.过点P作PQ∥AB,交AC于点Q,以PQ为边作等边三角形PQE,且点C,E在PQ同侧.设点P的运动时间为t(s)(t>0),△PQE与△ABC重合部分图形的面积为S(cm2).
(1)当点P在线段AD上运动时,判断△APQ的形状(不必证明),并直接写出AQ的长(用含t的代数式表示).
(2)当点E与点C重合时,求t的值.
(3)求S关于t的函数解析式,并写出自变量t的取值范围.
26.(10分)小明利用一次函数和二次函数知识,设计了一个计算程序,其程序框图如图(1)所示,输入x的值为﹣2时,输出y的值为1;输入x的值为2时,输出y的值为3;输入x的值为3时,输出y的值为6.
(1)直接写出k,a,b的值.
(2)小明在平面直角坐标系中画出了关于x的函数图象,如图(2).
Ⅰ.当y随x的增大而增大时,求x的取值范围.
Ⅱ.若关于x的方程ax2+bx+3﹣t=0(t为实数),在0<x<4时无解,求t的取值范围.
Ⅲ.若在函数图象上有点P,Q(P与Q不重合).P的横坐标为m,Q的横坐标为﹣m+1.小明对P,Q之间(含P,Q两点)的图象进行研究,当图象对应函数的最大值与最小值均不随m的变化而变化,直接写出m的取值范围.
参考答案
一、单项选择题(每小题2分,共12分)
1.解:(﹣3)×2=﹣6,故A选项错误;
(﹣3)×1=﹣3,故B选项错误;
(﹣3)×0=0,故C选项错误;
(﹣3)×(﹣1)=3,故D选项正确;
故选:D.
2.解:2040000000=2.04×109.
故选:B.
3.解:这个几何体的主视图与左视图相同,俯视图与主视图和左视图不相同,
故选:A.
4.解:A、(x﹣2)2=﹣1化简为方程x2﹣4x+5=0,
∵a=1,b=﹣4,c=5,
∴Δ=(﹣4)2﹣4×1×5=﹣4<0,
此方程没有实数根,不符合题意;
B、(x﹣2)2=0,化简为x2﹣4x+4=0,
∵a=1,b=﹣4,c=4,
∴Δ=(﹣4)2﹣4×1×4=0,
∴此方程有两个相等实数根,符合题意;
C、(x﹣2)2=1,化简为方程x2﹣4x+3=0中,
∵a=1,b=﹣4,c=3,
∴Δ=(﹣4)2﹣4×1×3=4>0,
∴此方程有两个不相等的实数根,不符合题意;
D、方程(x﹣2)2=2,化简为可化为x2﹣4x+2=0,
∵a=1,b=﹣4,c=2,
∴Δ=42﹣4×1×2=16﹣8=8>0,
∴此方程有两个不相等的实数根,不符合题意.
故选:B.
5.解:∵点A的坐标为(﹣4,0),点C的坐标为(0,2),
∴OA=4,OC=2,
∵四边形ABCO是矩形,
∴BC=OA=4,
∵将矩形OABC绕点O顺时针旋转90°,得到矩形OA′B′C′,
∴OC′=OC=2,B′C′=BC=4,
∴点B′的坐标为(2,4).
故选:C.
6.解:∵BE∥AD,
∴∠ADC=∠BEC=50°,
∵四边形ABCD内接于⊙O,
∴∠ABC=180°﹣∠ADC=130°.
故选:C.
二、填空题(每小题3分,共24分)
7.解:∵>0,1>0,
∴x+1>0,即x>﹣1,
则满足条件x的值可以为0(答案不唯一).
故答案为:0(答案不唯一).
8.解:a2﹣3a=a(a﹣3).
故答案为:a(a﹣3).
9.解:,
由①得:x>2,
由②得:x<3,
∴不等式组的解集是:2<x<3.
故答案为:2<x<3.
10.解:其中蕴含的数学道理是两点之间,线段最短,
故答案为:两点之间,线段最短.
11.解:由题意得:180°×(6﹣2)÷6=120°,
故答案为:120.
12.解:∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°,AD=BC,
∵∠FEO=45°,
∴∠FEO=∠DAC,
∴EF∥AD,
∵点E是OA的中点,
∴点F是OD的中点,
∴EF是△AOD的中位线,
∴EF=AD,
∴EF=BC,
即,
故答案为:.
13.解:在Rt△AB'C中,由勾股定理得,
AC2+B'C2=AB'2,
即x2+22=(x+0.5)2,
故答案为:x2+22=(x+0.5)2.
14.解:阴影部分的面积为:=11π(m2).
故答案为:11π.
三、解答题(每小题5分,共20分)
15.解:(a+1)(a﹣1)+a2+1
=a2﹣1+a2+1
=2a2
∵'
∴原式=2×()2=6.
16.解:把“滑雪”“滑雪圈”“雪地摩托”三个项目分别记为A、B、C,
画树状图如下:
共有9种等可能的结果,其中幸运游客小明与小亮恰好抽中同一个项目的结果有3种,
∴幸运游客小明与小亮恰好抽中同一个项目的概率为=.
17.证明:∵点O是AB的中点,
∴AO=OB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠E=∠BCO,
又∠AOE=∠BOC,
∴△AOE≌△BOC(AAS),
∴AE=BC.
18.解:设白色琴键的个数为x个,黑色琴键的个数为y个,
由题意得:,
解得:,
答:白色琴键的个数为52个,黑色琴键的个数为36个.
四、解答题(每小题7分,共28分)
19.解:(1)如图①所示,直线GH与直线EF即为所求;
(2)如图②所示,直线AB即为所求.
20.解:(1)设I=,
由题意得:K=RI=36,
∴这个反比例函数的解析式为I=;
(2)电阻R为3Ω时,I==12A.
21.解:(1)39218﹣30733=8485(元),
答:2019﹣2023年全国居民人均可支配收入中,收入最高的一年比收入最低多8485元;
(2)把2019﹣2023年全国居民人均可支配收入从小到大排列,排在中间的数是2021年人均可支配收入,
所以2019﹣2023年全国居民人均可支配收入的中位数是35128元;
(3)由折线统计图可知,
2019﹣2023年全国居民人均可支配收入呈逐年上升趋势,故①说法正确;
因为2019﹣2023年全国居民人均可支配收入呈逐年上升趋势,所以这5年中,2019年全国居民人均可支配收入最低,故②说法错误.
故答案为:①.
22.解:过点C作CF⊥AB,垂足为F.
∵AB⊥BD,CF⊥AB,DC⊥BD,
∴∠CDB=∠B=∠CFB=90°.
∴四边形CDBF是矩形.
∴BF=CD,CF=BD=873m.
∵CF∥BD∥AE,
∴∠EAC=∠ACF=37°,∠EAD=∠ADB=45°.
在Rt△ACF中,
∵tan∠ACF=,
∴AF=tan∠ACF CF
=tan37°×873
≈0.75×873
≈654.75(m).
在Rt△DBA中,
∵tan∠ADB=,
∴AB=tan∠ADB BD
=tan45°×873
=1×873
=873(m).
∴CD=FB=AB﹣AF
=873﹣654.75
=218.25
≈218.3(m).
答:吉塔的高度CD约为218.3m.
五、解答题(每小题8分,共16分)
23.解:(1)它们在同一条直线上,
设y=kx+b,
则:,
解得:,
所以这条直线所对应的函数解析式为y=5x+33;
(2)当y=213mm时,213=5x+33,
解得:x=36,
所以当凳面宽度为213mm时,以对称轴为基准向两边各取相同的长度是36mm.
24.解:(1)∵在△ABC中,AB=AC,BD⊥AC,CD=2,
∴AD=CD=2,
∴AC=4,
∴S△ABC=AC BD=2.
故答案为:2.
(2)∵在菱形S菱形A'B'C'D'A'B'C'D'中,A'C'=4,B'D'=2,
∴S菱形A'B'C'D'=A'C' B'D'=4,
故答案为:4.
(3)∵EG⊥FH,
∴S△EFG=EG FO,S△EHG=EG HO,
∴S四边形EFGH=S△EFG+S△EHG=EG FO+EG HO=EG FH=,
故答案为:.
猜想:S四边形EFGH=,
证明:∴S△EFG=EG FO,S△EHG=EG HO,
∴S四边形EFGH=S△EFG+S△EHG=EG FO+EG HO=EG FH=.
(4)根据尺规作图可知:∠QPM=∠MKN,
∵在△MNK中,MN=3,KN=4,MK=5,
∴MK2=MN2+KN2,
∴△MNK是直角三角形,且∠MNK=90°,
∴∠NMK+∠MKN=90°,
∵∠QPM=∠MKN,
∴∠NMK+∠QPM=90°,
∴MK⊥PQ,
∵PQ=KN=4,MK=5,
∴根据(3)中结论得S四边形MPKQ=MK PQ=10.
六、解答题(每小题10分,共20分)
25.解:(1)如图,过Q作QH⊥AD于点H,
∵PQ∥AB,
∴∠BAD=∠QAP,
∵AD是角平分线,
∴∠CAD=∠BAD,
∴∠CAD=∠QAP,
∴QA=QP,
∴△APQ是等腰三角形.
∵QH⊥AP,
∴AH=AP=,
∵∠CAD=30°,
∴AQ==t,
故△APQ是等腰三角形,AQ=t.
(2)如图所示,E、C重合时图形.
∵△PQE是等边三角形,
∴QE=QP,
由(1)得QA=QP,
∴AE=2AQ,即2t=3,
∴t=.
(3)①当点P在AD上,点E在AC上时,重合部分是等边三角形PQE,如图作PG⊥QE于点G,
∵∠PAQ=30°,
∴PG=AP=t,
∵△PQE是等边三角形,
∴QE=PQ=AQ=t,
∴S=QE PG=.
由(2)知当点EC重合时,t=,
∴S=(0<t≤).
②当点P在AD上,点E在AC延长线上时,重合部分时四边形PQCF.
在Rt△FCE中,CE=2t﹣3,∠E=60°,
∴CF=CE tan60°=(2t﹣3),
∴S△PCE=(2t﹣3) (2t﹣3)=(2t﹣3)2,
∴S=S△PAC﹣S△PCE=﹣(2t﹣3)2=﹣t2+6t﹣(<t<2).
③当点P在DB上,重合部分时直角三角形PQC,
S=CQ CP=(t﹣1) (t﹣1)=(t﹣1)2,(2≤t≤4).
综上所述,S=.
26.(1)解:∵x=﹣2<0,
∴将 x=﹣2,y=1 代入 y=kx+3,得:﹣2k+3=1,解得:k=1,
∵x=2>0,x=3>0,
将x=2,y=3和x=3,y=6分别代入 y=ax2+bx+3 得:,
解得:;
故:a=1,b=﹣2,k=1.
(2)解:I:∵k=1,a=1,b=﹣2,
∴一次函数解析式为:y=x+3,二次函数解析式为:y=x2﹣2x+3,
当x>0时,y=x2﹣2x+3,其对称轴为直线x=1,开口向上,
∴x≥1时,y随着x的增大而增大;
当x≤0时,y=x+3,k=1>0,
∴x≤0时,y随着x的增大而增大,
综上,x的取值范围:x≤0或x≥1;
Ⅱ:∵ax2+bx+3﹣t=0在0<x<4时无解,
∴ax2+bx+3=t,在0<x<4时无解,
∴问题转化为抛物线 y=x2﹣2x+3 与直线y=t在0<x<4时无交点,
∵对于 y=x2﹣2x+3,当x=1时,y=2,
∴顶点为(1,2),
如图:
∴当t=2时,抛物线 y=x2﹣2x+3 与直线y=t在0<x<4时正好一个交点,
∴当t<2时,抛物线 y=x2﹣2x+3 与直线y=t在0<x<4时没有交点;
当x=4,y=16﹣8+3=11,
∴当t=11时,抛物线 y=x2﹣2x+3 与直线y=t在0<x≤4时正好一个交点,
∴当t≥11时,抛物线 y=x2﹣2x+3 与直线y=t在0<x<4时没有交点,
∴当t<2或t≥11时,抛物线 y=x2﹣2x+3 与直线y=t在0<x<4时没有交点,
即:当t<2或t≥11时,关于x的方程 ax2+bx+3﹣t=0 (t为实数),在0<x<4时无解;
Ⅲ:∵xP=m,xQ=﹣m+1,
∴,
∴点P、Q关于直线 对称,
当 x=1,y最小值=1﹣2+3=2,
当 x=0时,y最大值=3,
∵当图象对应函数的最大值与最小值均不随m的变化而变化,而当 x=2 时,y=3,x=﹣1 时,y=2,
∴①当 如图:
由题意得:,
∴1≤m≤2;
②当 ,如图:
由题意得:,
∴﹣1≤m≤0,
综上:﹣1≤m≤0或1≤m≤2.
同课章节目录
