鲁教版九年级数学下册第5章5.10圆锥的侧面积学案(含答案)
文档属性
| 名称 | 鲁教版九年级数学下册第5章5.10圆锥的侧面积学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 98.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-22 00:00:00 | ||
图片预览

文档简介
鲁教版九年级数学下册第五单元5.10圆锥的侧面积同步辅导学案(含答案)
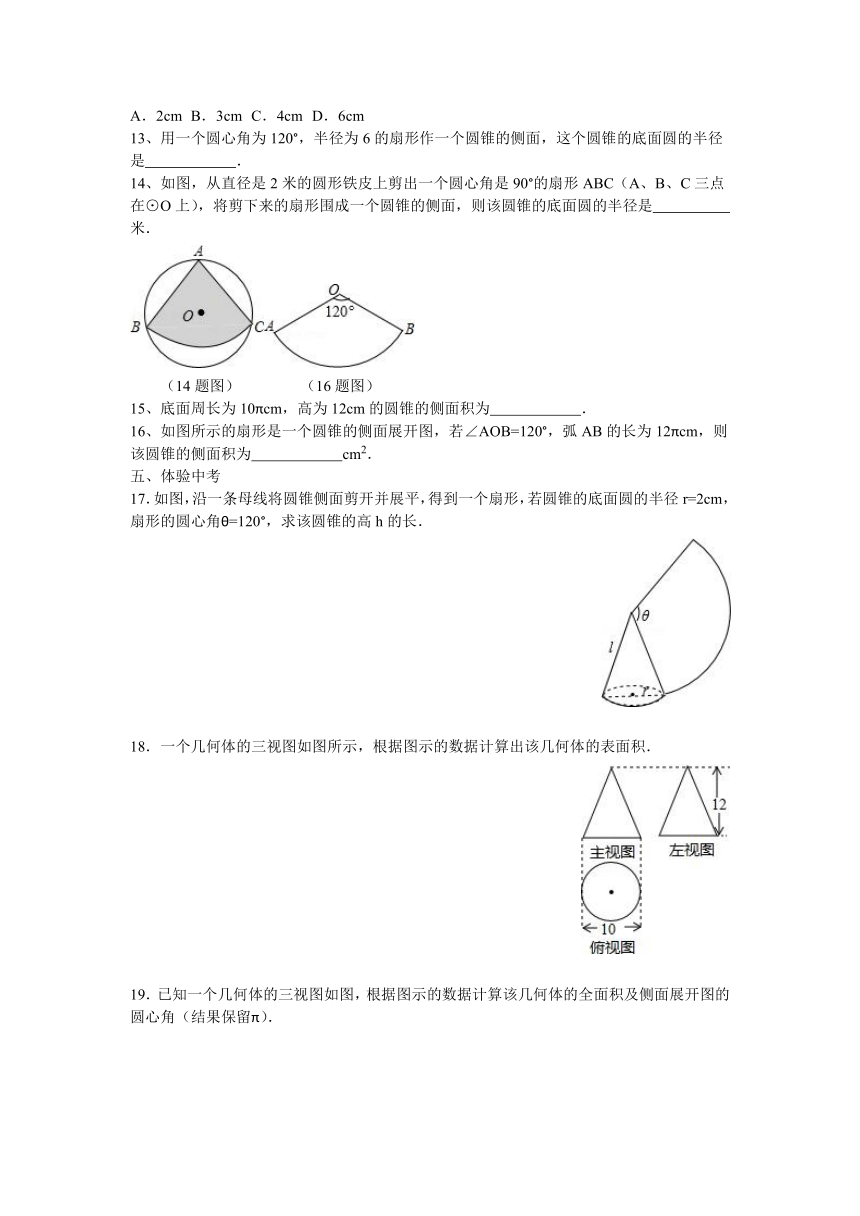
一、知识梳理
1、圆锥的侧面展开图是 。
2、圆锥的侧面展开图的计算公式: 。全面积的计算公式: 。
3、圆锥的的底面周长就是侧面展开图的 。
二、典例精析
1、已知圆锥的底面的半径为3cm,高为4cm,则它的侧面积为( )
A.15πcm2 B.16πcm2 C.19πcm2 D.24πcm2
2、已知圆锥的底面圆半径为3,母线长为5,则圆锥的全面积是 .
3、若一个圆锥的侧面展开图是半径为18cm,圆心角为240°的扇形,则这个圆锥的底面半径长是( )
A.6cm B.9cm C.12cm D.18cm
4、已知一块圆心角为300°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥的底面圆的直径是80cm,则这块扇形铁皮的半径是( )
A.24cm B.48cm C.96cm D.192cm
三、拔高训练
5、如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )
A.288° B.144° C.216° D.120°
(5题图) (6题图) (7题图) (8题图)
6、如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( )
A.5cm B.10cm C.20cm D.5πcm
7、如图,Rt△ABC中,∠ACB=90°,AC=BC=2,若把Rt△ABC绕边AB所在直线旋转一周,则所得几何体的表面积为 (结果保留π).
8、一个几何体的三视图如图,根据图示的数据计算该几何体的全面积为 .(结果保留π)
四、对应训练
9、圆锥的侧面展开图是一个弧长为12π的扇形,则这个圆锥底面积的半径是( )
A.24 B.12 C.6 D.3
10、将圆心角为90°,面积为4πcm2的扇形围成一个圆锥的侧面,则所围成的圆锥的底面半径为( )
A.1cm B.2cm C.3cm D.4cm
11、一个圆锥的侧面展开图是半径为6,圆心角为120°的扇形,那么这个圆锥的底面圆的半径为( )
A.1 B.2 C.3 D.4
12、已知圆锥的侧面积是20πcm2,母线长为5cm,则圆锥的底面半径为( )
A.2cm B.3cm C.4cm D.6cm
13、用一个圆心角为120°,半径为6的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径是 .
14、如图,从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A、B、C三点在⊙O上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径是 米.
(14题图) (16题图)
15、底面周长为10πcm,高为12cm的圆锥的侧面积为 .
16、如图所示的扇形是一个圆锥的侧面展开图,若∠AOB=120°,弧AB的长为12πcm,则该圆锥的侧面积为 cm2.
五、体验中考
17.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,求该圆锥的高h的长.
18.一个几何体的三视图如图所示,根据图示的数据计算出该几何体的表面积.
19.已知一个几何体的三视图如图,根据图示的数据计算该几何体的全面积及侧面展开图的圆心角(结果保留π).
20.已知圆锥的底面半径为r=20cm,高h=cm,现在有一只蚂蚁从底边上一点A出发.在侧面上爬行一周又回到A点,求蚂蚁爬行的最短距离.
21.如图,一个圆锥的高为cm,侧面展开图是半圆,求:
(1)圆锥的底面半径r与母线R之比;
(2)圆锥的全面积.
参考答案
1、A;2、24π;3、C; 4、B;5、A; 6、B; 7、8π; 8、24π;9、C;10、A;
11、B;12、C;13、2;14、;15、65πcm2;16、108π;
17.解:如图,由题意得:,而r=2,∴AB=6,
∴由勾股定理得:
AO2=AB2﹣OB2,而AB=6,OB=2,∴AO=4.即该圆锥的高为4.
18.解:由三视图可知该几何体是圆锥,圆锥的高为12,圆锥的底面圆的半径为5,
所以圆锥的母线长==13,
所以圆锥的表面积=π?52+?2π?5?13=90π.
19.解:∵如图所示可知,圆锥的高为4,底面圆的直径为6,
∴圆锥的母线为:5,
∴根据圆锥的侧面积公式:πrl=π×3×5=15π,
底面圆的面积为:πr2=9π,
∴该几何体的表面积为24π.
20.解:设扇形的圆心角为n,圆锥的顶为E,
∵r=20cm,h=20cm∴由勾股定理可得母线l==80cm,
而圆锥侧面展开后的扇形的弧长为2×20π=,∴n=90°
即△EAA′是等腰直角三角形,∴由勾股定理得:AA'==80cm.
答:蚂蚁爬行的最短距离为80cm.
21.解:(1)由题意可知∴,R=2r(3分)r:R=r:2r=1:2;
(2)在Rt△AOC中,
∵R2=r2+h2∴,4r2=r2+27r2=9,r=±3∵r>0∴r=3,R=6
∴S侧=πRr=18π(cm2)(cm2)
∴S全=S侧+S底=18π+9π=27π(cm2).
一、知识梳理
1、圆锥的侧面展开图是 。
2、圆锥的侧面展开图的计算公式: 。全面积的计算公式: 。
3、圆锥的的底面周长就是侧面展开图的 。
二、典例精析
1、已知圆锥的底面的半径为3cm,高为4cm,则它的侧面积为( )
A.15πcm2 B.16πcm2 C.19πcm2 D.24πcm2
2、已知圆锥的底面圆半径为3,母线长为5,则圆锥的全面积是 .
3、若一个圆锥的侧面展开图是半径为18cm,圆心角为240°的扇形,则这个圆锥的底面半径长是( )
A.6cm B.9cm C.12cm D.18cm
4、已知一块圆心角为300°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥的底面圆的直径是80cm,则这块扇形铁皮的半径是( )
A.24cm B.48cm C.96cm D.192cm
三、拔高训练
5、如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )
A.288° B.144° C.216° D.120°
(5题图) (6题图) (7题图) (8题图)
6、如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( )
A.5cm B.10cm C.20cm D.5πcm
7、如图,Rt△ABC中,∠ACB=90°,AC=BC=2,若把Rt△ABC绕边AB所在直线旋转一周,则所得几何体的表面积为 (结果保留π).
8、一个几何体的三视图如图,根据图示的数据计算该几何体的全面积为 .(结果保留π)
四、对应训练
9、圆锥的侧面展开图是一个弧长为12π的扇形,则这个圆锥底面积的半径是( )
A.24 B.12 C.6 D.3
10、将圆心角为90°,面积为4πcm2的扇形围成一个圆锥的侧面,则所围成的圆锥的底面半径为( )
A.1cm B.2cm C.3cm D.4cm
11、一个圆锥的侧面展开图是半径为6,圆心角为120°的扇形,那么这个圆锥的底面圆的半径为( )
A.1 B.2 C.3 D.4
12、已知圆锥的侧面积是20πcm2,母线长为5cm,则圆锥的底面半径为( )
A.2cm B.3cm C.4cm D.6cm
13、用一个圆心角为120°,半径为6的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径是 .
14、如图,从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A、B、C三点在⊙O上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径是 米.
(14题图) (16题图)
15、底面周长为10πcm,高为12cm的圆锥的侧面积为 .
16、如图所示的扇形是一个圆锥的侧面展开图,若∠AOB=120°,弧AB的长为12πcm,则该圆锥的侧面积为 cm2.
五、体验中考
17.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,求该圆锥的高h的长.
18.一个几何体的三视图如图所示,根据图示的数据计算出该几何体的表面积.
19.已知一个几何体的三视图如图,根据图示的数据计算该几何体的全面积及侧面展开图的圆心角(结果保留π).
20.已知圆锥的底面半径为r=20cm,高h=cm,现在有一只蚂蚁从底边上一点A出发.在侧面上爬行一周又回到A点,求蚂蚁爬行的最短距离.
21.如图,一个圆锥的高为cm,侧面展开图是半圆,求:
(1)圆锥的底面半径r与母线R之比;
(2)圆锥的全面积.
参考答案
1、A;2、24π;3、C; 4、B;5、A; 6、B; 7、8π; 8、24π;9、C;10、A;
11、B;12、C;13、2;14、;15、65πcm2;16、108π;
17.解:如图,由题意得:,而r=2,∴AB=6,
∴由勾股定理得:
AO2=AB2﹣OB2,而AB=6,OB=2,∴AO=4.即该圆锥的高为4.
18.解:由三视图可知该几何体是圆锥,圆锥的高为12,圆锥的底面圆的半径为5,
所以圆锥的母线长==13,
所以圆锥的表面积=π?52+?2π?5?13=90π.
19.解:∵如图所示可知,圆锥的高为4,底面圆的直径为6,
∴圆锥的母线为:5,
∴根据圆锥的侧面积公式:πrl=π×3×5=15π,
底面圆的面积为:πr2=9π,
∴该几何体的表面积为24π.
20.解:设扇形的圆心角为n,圆锥的顶为E,
∵r=20cm,h=20cm∴由勾股定理可得母线l==80cm,
而圆锥侧面展开后的扇形的弧长为2×20π=,∴n=90°
即△EAA′是等腰直角三角形,∴由勾股定理得:AA'==80cm.
答:蚂蚁爬行的最短距离为80cm.
21.解:(1)由题意可知∴,R=2r(3分)r:R=r:2r=1:2;
(2)在Rt△AOC中,
∵R2=r2+h2∴,4r2=r2+27r2=9,r=±3∵r>0∴r=3,R=6
∴S侧=πRr=18π(cm2)(cm2)
∴S全=S侧+S底=18π+9π=27π(cm2).
