2024年山东省威海市中考数学真题(含答案)
文档属性
| 名称 | 2024年山东省威海市中考数学真题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 626.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 16:26:34 | ||
图片预览



文档简介
2024年山东省威海市中考数学试题
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个是正确的.每小题选对得3分,选错、不选或多选,均不得分)
1.一批食品,标准质量为每袋454g.现随机抽取4个样品进行检测,把超过标准质量的克数用正数表示,不足的克数用负数表示.那么,最接近标准质量的是( )
A.+7 B.﹣5 C.﹣3 D.10
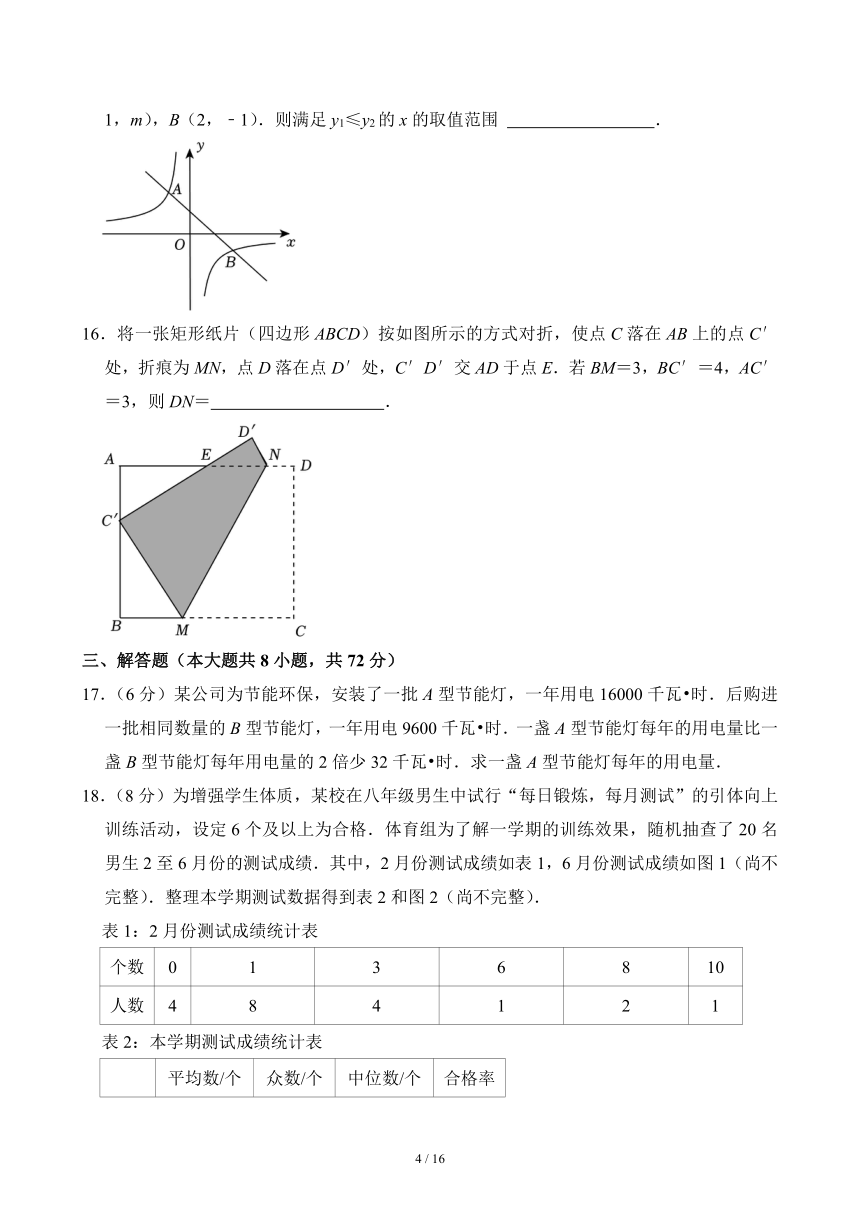
2.据央视网2023年10月11日消息,中国科学技术大学中国科学院量子创新研究院与上海微系统所、国家并行计算机工程技术研究中心合作,成功构建了255个光子的量子计算原型机“九章三号”,再度刷新了光量子信息的技术水平和量子计算优越性的世界纪录.“九章三号”处理高斯玻色取样的速度比上一代“九章二号”提升一百万倍,在百万分之一秒时间内所处理的最高复杂度的样本,需要当前最强的超级计算机花费超过二百亿年的时间.将“百万分之一”用科学记数法表示为( )
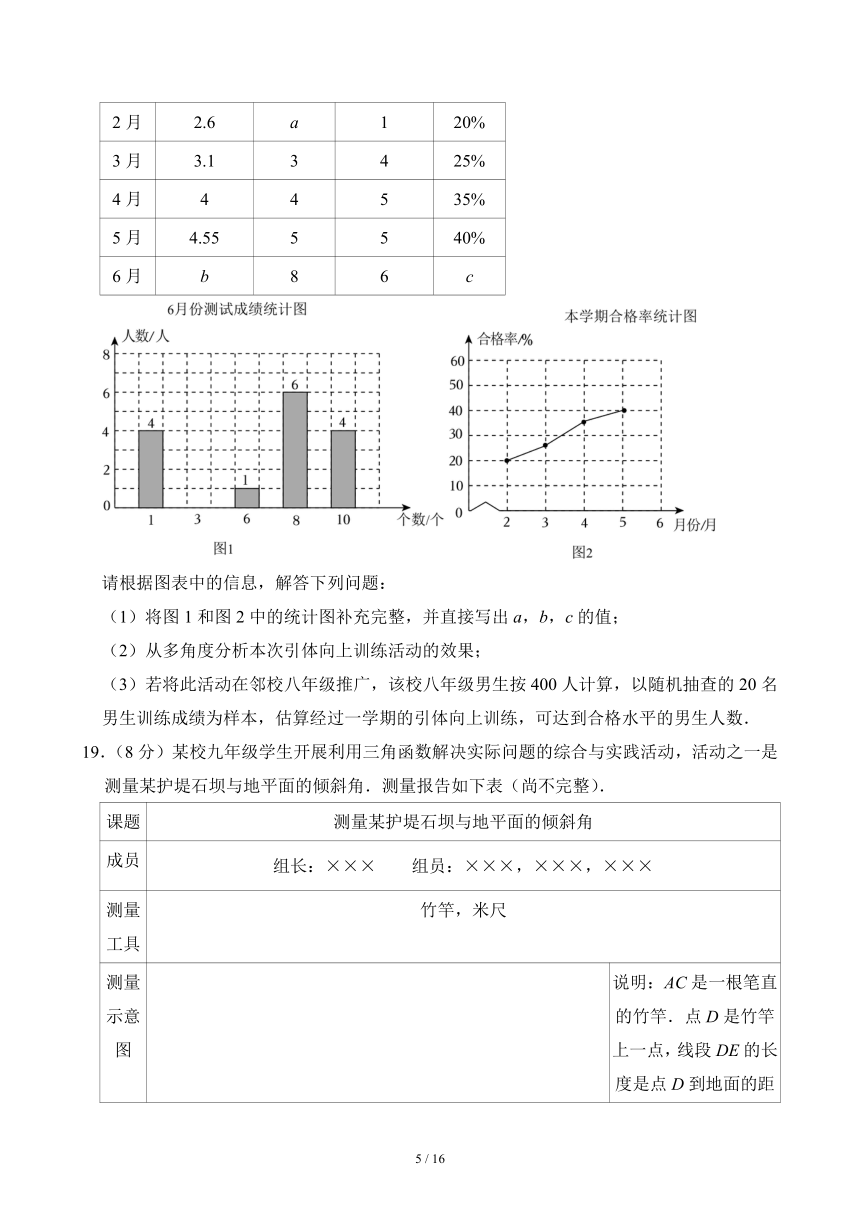
A.1×10﹣5 B.1×10﹣6 C.1×10﹣7 D.1×10﹣8
3.下列各数中,最小的数是( )
A.﹣2 B.﹣(﹣2) C. D.
4.下列运算正确的是( )
A.x5+x5=x10 B.m+n2
C.a6÷a2=a4 D.(﹣a2)3=﹣a5
5.下列几何体都是由四个大小相同的小正方体搭成的.其中主视图、左视图和俯视图完全相同的是( )
A. B. C. D.
6.如图,在扇形AOB中,∠AOB=90°,点C是AO的中点.过点C作CE⊥AO交于点E,过点E作ED⊥OB,垂足为点D.在扇形内随机选取一点P,则点P落在阴影部分的概率是( )
A. B. C. D.
7.定义新运算:
①在平面直角坐标系中,{a,b}表示动点从原点出发,沿着x轴正方向(a≥0)或负方向(a<0)平移|a|个单位长度,再沿着y轴正方向(b≥0)或负方向(b<0)平移|b|个单位长度.例如,动点从原点出发,沿着x轴负方向平移2个单位长度,再沿着y轴正方向平移1个单位长度,记作(﹣2,1).
②加法运算法则:{a,b}+{c,d}={a+c,b+d},其中a,b,c,d为实数.
若{3,5}+{m,n}={﹣1,2},则下列结论正确的是( )
A.m=2,n=7 B.m=﹣4,n=﹣3 C.m=4,n=3 D.m=﹣4,n=3
8.《九章算术》是我国古老的数学经典著作,书中提到这样一道题目:以绳测井.若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.绳长、井深各几何?题目大意是:用绳子测量水井的深度.如果将绳子折成三等份,一份绳长比井深多4尺;如果将绳子折成四等份,一份绳长比井深多1尺.绳长、井深各是多少尺?
若设绳长x尺,井深y尺,则符合题意的方程组是( )
A. B.
C. D.
9.如图,在 ABCD中,对角线AC,BD交于点O,点E在BC上,点F在CD上,连接AE,AF,EF,EF交AC于点G.下列结论错误的是( )
A.若,则EF∥BD
B.若AE⊥BC,AF⊥CD,AE=AF,则EF∥BD
C.若EF∥BD,CE=CF,则∠EAC=∠FAC
D.若AB=AD,AE=AF,则EF∥BD
10.同一条公路连接A,B,C三地,B地在A,C两地之间.甲、乙两车分别从A地、B地同时出发前往C地.甲车速度始终保持不变,乙车中途休息一段时间,继续行驶.如图表示甲、乙两车之间的距离y(km)与时间x(h)的函数关系.下列结论正确的是( )
A.甲车行驶h与乙车相遇
B.A,C两地相距220km
C.甲车的速度是70km/h
D.乙车中途休息36分钟
二、填空题(本大题共6小题,每小题3分,共18分.只要求填出最后结果)
11.计算: .
12.因式分解:(x+2)(x+4)+1= .
13.如图,在正六边形ABCDEF中,AH∥FG,BI⊥AH,垂足为点I.若∠EFG=20°,则∠ABI= .
14.计算: .
15.如图,在平面直角坐标系中,直线y1=ax+b(a≠0)与双曲线y2(k≠0)交于点A(﹣1,m),B(2,﹣1).则满足y1≤y2的x的取值范围 .
16.将一张矩形纸片(四边形ABCD)按如图所示的方式对折,使点C落在AB上的点C′处,折痕为MN,点D落在点D′处,C′D′交AD于点E.若BM=3,BC′=4,AC′=3,则DN= .
三、解答题(本大题共8小题,共72分)
17.(6分)某公司为节能环保,安装了一批A型节能灯,一年用电16000千瓦 时.后购进一批相同数量的B型节能灯,一年用电9600千瓦 时.一盏A型节能灯每年的用电量比一盏B型节能灯每年用电量的2倍少32千瓦 时.求一盏A型节能灯每年的用电量.
18.(8分)为增强学生体质,某校在八年级男生中试行“每日锻炼,每月测试”的引体向上训练活动,设定6个及以上为合格.体育组为了解一学期的训练效果,随机抽查了20名男生2至6月份的测试成绩.其中,2月份测试成绩如表1,6月份测试成绩如图1(尚不完整).整理本学期测试数据得到表2和图2(尚不完整).
表1:2月份测试成绩统计表
个数 0 1 3 6 8 10
人数 4 8 4 1 2 1
表2:本学期测试成绩统计表
平均数/个 众数/个 中位数/个 合格率
2月 2.6 a 1 20%
3月 3.1 3 4 25%
4月 4 4 5 35%
5月 4.55 5 5 40%
6月 b 8 6 c
请根据图表中的信息,解答下列问题:
(1)将图1和图2中的统计图补充完整,并直接写出a,b,c的值;
(2)从多角度分析本次引体向上训练活动的效果;
(3)若将此活动在邻校八年级推广,该校八年级男生按400人计算,以随机抽查的20名男生训练成绩为样本,估算经过一学期的引体向上训练,可达到合格水平的男生人数.
19.(8分)某校九年级学生开展利用三角函数解决实际问题的综合与实践活动,活动之一是测量某护堤石坝与地平面的倾斜角.测量报告如下表(尚不完整).
课题 测量某护堤石坝与地平面的倾斜角
成员 组长:××× 组员:×××,×××,×××
测量工具 竹竿,米尺
测量示意图
说明:AC是一根笔直的竹竿.点D是竹竿上一点,线段DE的长度是点D到地面的距离.∠α是要测量的倾斜角
测量数据
…… ……
(1)设AB=a,BC=b,AC=c,CE=d,DE=e,CD=f,BE=g,AD=h,请根据表中的测量示意图,从以上线段中选出你认为需要测量的数据,把表示数据的小写字母填写在“测量数据”一栏.
(2)根据(1)中选择的数据,写出求∠α 的一种三角函数值的推导过程.
(3)假设sinα≈0.86,cosα≈0.52,tanα≈1.66,根据(2)中的推导结果,利用计算器求出∠α的度数.你选择的按键顺序为 .
20.(9分)感悟 如图1,在△ABE中,点C,D在边BE上,AB=AE,BC=DE.求证:∠BAC=∠EAD.
应用 (1)如图2,用直尺和圆规在直线BC上取点D,点E(点D在点E的左侧),使得∠EAD=∠BAC,且DE=BC(不写作法,保留作图痕迹);
(2)如图3,用直尺和圆规在直线AC上取一点D,在直线BC上取一点E,使得∠CDE=∠BAC,且DE=AB(不写作法,保留作图痕迹).
21.(9分)定义 我们把数轴上表示数a的点与原点的距离叫做数a的绝对值.数轴上表示数a,b的点A,B之间的距离AB=a﹣b(a≥b).特别的,当a≥0时,表示数a的点与原点的距离等于a﹣0.当a<0时,表示数a的点与原点的距离等于0﹣a.
应用 如图,在数轴上,动点A从表示﹣3的点出发,以1个单位/秒的速度沿着数轴的正方向运动.同时,动点B从表示12的点出发,以2个单位/秒的速度沿着数轴的负方向运动.
(1)经过多长时间,点A,B之间的距离等于3个单位长度?
(2)求点A,B到原点距离之和的最小值.
22.(10分)如图,已知AB是⊙O的直径,点C,D在⊙O上,且BC=CD.点E是线段AB延长线上一点,连接EC并延长交射线AD于点F.∠FEG的平分线EH交射线AC于点H,∠H=45°.
(1)求证:EF是⊙O的切线;
(2)若BE=2,CE=4,求AF的长.
23.(10分)如图,在菱形ABCD中,AB=10cm,∠ABC=60°,E为对角线AC上一动点,以DE为一边作∠DEF=60°,EF交射线BC于点F,连接BE,DF.点E从点C出发,沿CA方向以每秒2cm的速度运动至点A处停止.设△BEF的面积为y cm2,点E的运动时间为x秒.
(1)求证:BE=EF;
(2)求y与x的函数表达式,并写出自变量x的取值范围;
(3)求x为何值时,线段DF的长度最短.
24.(12分)已知抛物线y=x2+bx+c(b<0)与x轴交点的坐标分别为(x1,0),(x2,0),且x1<x2.
(1)若抛物线y1=x2+bx+c+1(b<0)与x轴交点的坐标分别为(x3,0),(x4,0),且x3<x4,试判断下列每组数据的大小(填写<、=或>):
①x1+x2 x3+x4;②x1﹣x3 x2﹣x4;③x2+x3 x1+x4.
(2)若x1=1,2<x2<3,求b的取值范围;
(3)当0≤x≤1时,y=x2+bx+c(b<0)最大值与最小值的差为,求b的值.
2024年山东省威海市中考数学试题参考答案
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个是正确的.每小题选对得3分,选错、不选或多选,均不得分)
1.C
2.B
3.A
4.C
5.D
6.B
7.B
8.C
9.D
10.A
二、填空题(本大题共6小题,每小题3分,共18分.只要求填出最后结果)
11.
12.(x+3)2
13.50°
14.﹣x﹣2
15.﹣1≤x<0或x≥2
16.
三、解答题(本大题共8小题,共72分)
17.(6分)解:设一盏B型节能灯每年的用电量为x千瓦 时,则一盏A型节能灯每年的用电量为(2x﹣32)千瓦 时,
根据题意得:,
解得:x=96,
经检验,x=96是所列方程的解,且符合题意,
∴2x﹣32=2×96﹣32=160(千瓦 时).
答:一盏A型节能灯每年的用电量为160千瓦 时.
18.(8分)解:(1)6月测试成绩中,引体向上3个的人数为20﹣4﹣1﹣6﹣4=5(人),
补充统计图如下:
c100%=55%,
根据表2可得a=1,
b(4×1+5×3+1×6+6×8+4×10)=5.65,
(2)本次引体向上训练活动的效果明显,理由如下:
从平均数和合格率看,平均数和合格率逐月增加,
从中位数看,引体向上个数逐月增加,
从众数看,引体向上的个数越来越大(答案不唯一,合理即可);
(3)400×55%=220(人),
答:估算经过一学期的引体向上训练,可达到合格水平的男生人数约220人.
19.(8分)解:(1)需要的数据为:AB=a,AC=c,DE=e,CD=f;
(2)过点A作AM⊥CB于点M,则∠AMB=90°,
∵DE⊥CB,
∴DE∥AM,
∴△CDE∽△CAM,
∴,即,
∴,
∴;
(3)∵,
∴按键顺序为2ndF,sin,0, ,8,6,=,
故答案为:①.
20.(9分)解:感悟:过点A作AH⊥BE于点H,
∵AB=AE,BC=DE,
∴∠BAH=∠EAH,∠CAH=∠DAH,
∴∠BAC=∠DAE;
应用:(1)解:如图2:点D,E即为所求;
(2)点D,E即为所求.
21.(9分)解:(1)设经过x秒,点A,B之间的距离等于3个单位长度,
则:|(﹣3+x)﹣(12﹣2x)|=3,
解得:x=4或x=6,
答:经过4秒或6秒,点A,B之间的距离等于3个单位长度;
(2)设经过x秒,点A,B到原点距离之和为y,
则y=|﹣3+x|+|12﹣2x|,
当x≤3时,y=|﹣3+x|+|12﹣2x|=3﹣x+12﹣2x=﹣3x+15,
当x=3时,y值最小,为6,
当3<x≤6时,y=|﹣3+x|+|12﹣2x|=﹣3+x+12﹣2x=﹣x+9,
当x=6时,y值最小,为3,
当x>6时,y=|﹣3+x|+|12﹣2x|=﹣3+x﹣12+2x=3x﹣15,
当x=6时,y有极小值,为3,
综上所述,点A,B到原点距离之和的最小值为3.
22.(10分)(1)证明:如图,连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵BC=CD,
∴∠DAC=∠BAC,
∴∠OCA=∠DAC,
∴OC∥AF,
∵EH平分∠FEG,
∴∠FEH=∠GEH,
∵∠GEH=∠H+∠BAC,∠FEH=∠F+∠BAF,
∴2∠H+2∠BAC=∠F+∠BAF,
∴∠BAF=2∠BAC,
∴∠F=2∠H=90°,
∴∠OCE=∠F=90°,
即OC⊥EF,
∵OC是半径,
∴EF是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,即∠OCB+∠BCE=90°,
∴∠OBC+∠BAC=90°,
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠BCE=∠EAC,
∵∠CEB=∠CAE,
∴△BCE∽△CAE,
∴,
∴CE2=BE AE,即16=2AE,
解得AE=8,
∴AB=8﹣2=6,
在Rt△ABC中,AB=6,,
∴BC,AC,
∵∠F=∠ACB=90°,∠FAC=∠BAC,
∴△FAC∽△CAB,
∴,
∴AF.
23.(10分)(1)证明:设CD与EF相交于点M,
∵四边形ABCD为菱形,∴BC﹣=DC,∠BCE=∠DCE,AB∥CD,
∵∠ABC=60°,
∴∠DCF=60°,
在△BCE和△DCE中,
,
∴△BCE≌△DCE(SAS),
∴∠CBE=∠CDE,BE=DE,
∵∠DMF=∠DEF+∠CDE=∠DCF+∠CFE,
又∵∠DEF=∠DCF=60°,
∴∠CDE=∠CFE,
∴∠CBE=∠CFE,
∴BE=EF;
(2)解:过点E作EN⊥BC于N,
则∠ENC=90°,
∵BE=EF,
∴BF=2BN,
∵四边形ABCD为菱形,∠ABC=60°,
∴ВС=АВ=10cm,∠АСВ=∠BСD=60°,即∠ECN=60°,
∵CE=2x cm,
∴EN=CE sin60°=2x x(cm),CN=CE cos60°=2x x(cm),
∴BN=BC﹣CN=10﹣x(cm),
∴BF=2(10﹣x)cm,
∴уВF ЕN2(10﹣х)хх2+10х,
∵0<2x≤10,
∴0<x≤5,
∴yх2+10х(0<x≤5);
(3)解:∵BE=DE,BE=EF,
∴DE=EF,
∵∠DEF=60°,
∴△DEF为等边三角形,
∴DE=DF﹣EF,
∴BE=DF,
∴线段DF的长度最短,即BE的长度最短,当BE⊥AC时,BE取最短,如图,
∵四边形 ABCD是菱形,
∴АВ=ВС,
∵∠ABC=60°,
∴△ABC为等边三角形,
∴AE=AB=AC=10cm,
∵BE⊥AC,
∴CEAC=5cm,
∴x,
∴当x时,线段DF的长度最短.
24.(12分)解:(1)∵y=x2+bx+c(b<0)与x轴交点的坐标分别为(x1,0),(x2,0),且x1<x2,
∴x1+x2=﹣b,且抛物线开口向上,
∵ 与x轴交点的坐标分别为(x3,0),(x4,0),且x1<x4,
即y=x2+bx+c(b<0)向上平移1个单位,
∴x1<x3<x4<x2,且x1+x4=﹣b,
∴①x1+x2=x1+x4;
∵x2﹣x1>x4﹣x3
∴x2﹣x4>x1﹣x3,即②x1﹣x5<x2﹣x4;
∴x1+x3>x1+x4,即③x2+x3>x1+x4,
故答案为:=;<;>;
(2)∵x1=1,2<x2<3,
∴3<x2+x1<4
∴3<﹣b<4,
∴﹣4<b<﹣3;
(3)抛物线y=x2+bx+c(b<0)顶点坐标为,对称轴为直线,
当x=0时,y=c;
当x=1时,y=1+b+c;
①当在 x=0 取得最大值,在x=1取得最小值时,有,
解得;
②当在x=0取得最大值,在顶点取得最小值时,
有,
解得(舍去)或;
③当在x=1取得最大值,在顶点取得最小值时,
有,
解得(舍去)或,
综上所述,b的值为或或.
(
1
/
35
)
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个是正确的.每小题选对得3分,选错、不选或多选,均不得分)
1.一批食品,标准质量为每袋454g.现随机抽取4个样品进行检测,把超过标准质量的克数用正数表示,不足的克数用负数表示.那么,最接近标准质量的是( )
A.+7 B.﹣5 C.﹣3 D.10
2.据央视网2023年10月11日消息,中国科学技术大学中国科学院量子创新研究院与上海微系统所、国家并行计算机工程技术研究中心合作,成功构建了255个光子的量子计算原型机“九章三号”,再度刷新了光量子信息的技术水平和量子计算优越性的世界纪录.“九章三号”处理高斯玻色取样的速度比上一代“九章二号”提升一百万倍,在百万分之一秒时间内所处理的最高复杂度的样本,需要当前最强的超级计算机花费超过二百亿年的时间.将“百万分之一”用科学记数法表示为( )
A.1×10﹣5 B.1×10﹣6 C.1×10﹣7 D.1×10﹣8
3.下列各数中,最小的数是( )
A.﹣2 B.﹣(﹣2) C. D.
4.下列运算正确的是( )
A.x5+x5=x10 B.m+n2
C.a6÷a2=a4 D.(﹣a2)3=﹣a5
5.下列几何体都是由四个大小相同的小正方体搭成的.其中主视图、左视图和俯视图完全相同的是( )
A. B. C. D.
6.如图,在扇形AOB中,∠AOB=90°,点C是AO的中点.过点C作CE⊥AO交于点E,过点E作ED⊥OB,垂足为点D.在扇形内随机选取一点P,则点P落在阴影部分的概率是( )
A. B. C. D.
7.定义新运算:
①在平面直角坐标系中,{a,b}表示动点从原点出发,沿着x轴正方向(a≥0)或负方向(a<0)平移|a|个单位长度,再沿着y轴正方向(b≥0)或负方向(b<0)平移|b|个单位长度.例如,动点从原点出发,沿着x轴负方向平移2个单位长度,再沿着y轴正方向平移1个单位长度,记作(﹣2,1).
②加法运算法则:{a,b}+{c,d}={a+c,b+d},其中a,b,c,d为实数.
若{3,5}+{m,n}={﹣1,2},则下列结论正确的是( )
A.m=2,n=7 B.m=﹣4,n=﹣3 C.m=4,n=3 D.m=﹣4,n=3
8.《九章算术》是我国古老的数学经典著作,书中提到这样一道题目:以绳测井.若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.绳长、井深各几何?题目大意是:用绳子测量水井的深度.如果将绳子折成三等份,一份绳长比井深多4尺;如果将绳子折成四等份,一份绳长比井深多1尺.绳长、井深各是多少尺?
若设绳长x尺,井深y尺,则符合题意的方程组是( )
A. B.
C. D.
9.如图,在 ABCD中,对角线AC,BD交于点O,点E在BC上,点F在CD上,连接AE,AF,EF,EF交AC于点G.下列结论错误的是( )
A.若,则EF∥BD
B.若AE⊥BC,AF⊥CD,AE=AF,则EF∥BD
C.若EF∥BD,CE=CF,则∠EAC=∠FAC
D.若AB=AD,AE=AF,则EF∥BD
10.同一条公路连接A,B,C三地,B地在A,C两地之间.甲、乙两车分别从A地、B地同时出发前往C地.甲车速度始终保持不变,乙车中途休息一段时间,继续行驶.如图表示甲、乙两车之间的距离y(km)与时间x(h)的函数关系.下列结论正确的是( )
A.甲车行驶h与乙车相遇
B.A,C两地相距220km
C.甲车的速度是70km/h
D.乙车中途休息36分钟
二、填空题(本大题共6小题,每小题3分,共18分.只要求填出最后结果)
11.计算: .
12.因式分解:(x+2)(x+4)+1= .
13.如图,在正六边形ABCDEF中,AH∥FG,BI⊥AH,垂足为点I.若∠EFG=20°,则∠ABI= .
14.计算: .
15.如图,在平面直角坐标系中,直线y1=ax+b(a≠0)与双曲线y2(k≠0)交于点A(﹣1,m),B(2,﹣1).则满足y1≤y2的x的取值范围 .
16.将一张矩形纸片(四边形ABCD)按如图所示的方式对折,使点C落在AB上的点C′处,折痕为MN,点D落在点D′处,C′D′交AD于点E.若BM=3,BC′=4,AC′=3,则DN= .
三、解答题(本大题共8小题,共72分)
17.(6分)某公司为节能环保,安装了一批A型节能灯,一年用电16000千瓦 时.后购进一批相同数量的B型节能灯,一年用电9600千瓦 时.一盏A型节能灯每年的用电量比一盏B型节能灯每年用电量的2倍少32千瓦 时.求一盏A型节能灯每年的用电量.
18.(8分)为增强学生体质,某校在八年级男生中试行“每日锻炼,每月测试”的引体向上训练活动,设定6个及以上为合格.体育组为了解一学期的训练效果,随机抽查了20名男生2至6月份的测试成绩.其中,2月份测试成绩如表1,6月份测试成绩如图1(尚不完整).整理本学期测试数据得到表2和图2(尚不完整).
表1:2月份测试成绩统计表
个数 0 1 3 6 8 10
人数 4 8 4 1 2 1
表2:本学期测试成绩统计表
平均数/个 众数/个 中位数/个 合格率
2月 2.6 a 1 20%
3月 3.1 3 4 25%
4月 4 4 5 35%
5月 4.55 5 5 40%
6月 b 8 6 c
请根据图表中的信息,解答下列问题:
(1)将图1和图2中的统计图补充完整,并直接写出a,b,c的值;
(2)从多角度分析本次引体向上训练活动的效果;
(3)若将此活动在邻校八年级推广,该校八年级男生按400人计算,以随机抽查的20名男生训练成绩为样本,估算经过一学期的引体向上训练,可达到合格水平的男生人数.
19.(8分)某校九年级学生开展利用三角函数解决实际问题的综合与实践活动,活动之一是测量某护堤石坝与地平面的倾斜角.测量报告如下表(尚不完整).
课题 测量某护堤石坝与地平面的倾斜角
成员 组长:××× 组员:×××,×××,×××
测量工具 竹竿,米尺
测量示意图
说明:AC是一根笔直的竹竿.点D是竹竿上一点,线段DE的长度是点D到地面的距离.∠α是要测量的倾斜角
测量数据
…… ……
(1)设AB=a,BC=b,AC=c,CE=d,DE=e,CD=f,BE=g,AD=h,请根据表中的测量示意图,从以上线段中选出你认为需要测量的数据,把表示数据的小写字母填写在“测量数据”一栏.
(2)根据(1)中选择的数据,写出求∠α 的一种三角函数值的推导过程.
(3)假设sinα≈0.86,cosα≈0.52,tanα≈1.66,根据(2)中的推导结果,利用计算器求出∠α的度数.你选择的按键顺序为 .
20.(9分)感悟 如图1,在△ABE中,点C,D在边BE上,AB=AE,BC=DE.求证:∠BAC=∠EAD.
应用 (1)如图2,用直尺和圆规在直线BC上取点D,点E(点D在点E的左侧),使得∠EAD=∠BAC,且DE=BC(不写作法,保留作图痕迹);
(2)如图3,用直尺和圆规在直线AC上取一点D,在直线BC上取一点E,使得∠CDE=∠BAC,且DE=AB(不写作法,保留作图痕迹).
21.(9分)定义 我们把数轴上表示数a的点与原点的距离叫做数a的绝对值.数轴上表示数a,b的点A,B之间的距离AB=a﹣b(a≥b).特别的,当a≥0时,表示数a的点与原点的距离等于a﹣0.当a<0时,表示数a的点与原点的距离等于0﹣a.
应用 如图,在数轴上,动点A从表示﹣3的点出发,以1个单位/秒的速度沿着数轴的正方向运动.同时,动点B从表示12的点出发,以2个单位/秒的速度沿着数轴的负方向运动.
(1)经过多长时间,点A,B之间的距离等于3个单位长度?
(2)求点A,B到原点距离之和的最小值.
22.(10分)如图,已知AB是⊙O的直径,点C,D在⊙O上,且BC=CD.点E是线段AB延长线上一点,连接EC并延长交射线AD于点F.∠FEG的平分线EH交射线AC于点H,∠H=45°.
(1)求证:EF是⊙O的切线;
(2)若BE=2,CE=4,求AF的长.
23.(10分)如图,在菱形ABCD中,AB=10cm,∠ABC=60°,E为对角线AC上一动点,以DE为一边作∠DEF=60°,EF交射线BC于点F,连接BE,DF.点E从点C出发,沿CA方向以每秒2cm的速度运动至点A处停止.设△BEF的面积为y cm2,点E的运动时间为x秒.
(1)求证:BE=EF;
(2)求y与x的函数表达式,并写出自变量x的取值范围;
(3)求x为何值时,线段DF的长度最短.
24.(12分)已知抛物线y=x2+bx+c(b<0)与x轴交点的坐标分别为(x1,0),(x2,0),且x1<x2.
(1)若抛物线y1=x2+bx+c+1(b<0)与x轴交点的坐标分别为(x3,0),(x4,0),且x3<x4,试判断下列每组数据的大小(填写<、=或>):
①x1+x2 x3+x4;②x1﹣x3 x2﹣x4;③x2+x3 x1+x4.
(2)若x1=1,2<x2<3,求b的取值范围;
(3)当0≤x≤1时,y=x2+bx+c(b<0)最大值与最小值的差为,求b的值.
2024年山东省威海市中考数学试题参考答案
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个是正确的.每小题选对得3分,选错、不选或多选,均不得分)
1.C
2.B
3.A
4.C
5.D
6.B
7.B
8.C
9.D
10.A
二、填空题(本大题共6小题,每小题3分,共18分.只要求填出最后结果)
11.
12.(x+3)2
13.50°
14.﹣x﹣2
15.﹣1≤x<0或x≥2
16.
三、解答题(本大题共8小题,共72分)
17.(6分)解:设一盏B型节能灯每年的用电量为x千瓦 时,则一盏A型节能灯每年的用电量为(2x﹣32)千瓦 时,
根据题意得:,
解得:x=96,
经检验,x=96是所列方程的解,且符合题意,
∴2x﹣32=2×96﹣32=160(千瓦 时).
答:一盏A型节能灯每年的用电量为160千瓦 时.
18.(8分)解:(1)6月测试成绩中,引体向上3个的人数为20﹣4﹣1﹣6﹣4=5(人),
补充统计图如下:
c100%=55%,
根据表2可得a=1,
b(4×1+5×3+1×6+6×8+4×10)=5.65,
(2)本次引体向上训练活动的效果明显,理由如下:
从平均数和合格率看,平均数和合格率逐月增加,
从中位数看,引体向上个数逐月增加,
从众数看,引体向上的个数越来越大(答案不唯一,合理即可);
(3)400×55%=220(人),
答:估算经过一学期的引体向上训练,可达到合格水平的男生人数约220人.
19.(8分)解:(1)需要的数据为:AB=a,AC=c,DE=e,CD=f;
(2)过点A作AM⊥CB于点M,则∠AMB=90°,
∵DE⊥CB,
∴DE∥AM,
∴△CDE∽△CAM,
∴,即,
∴,
∴;
(3)∵,
∴按键顺序为2ndF,sin,0, ,8,6,=,
故答案为:①.
20.(9分)解:感悟:过点A作AH⊥BE于点H,
∵AB=AE,BC=DE,
∴∠BAH=∠EAH,∠CAH=∠DAH,
∴∠BAC=∠DAE;
应用:(1)解:如图2:点D,E即为所求;
(2)点D,E即为所求.
21.(9分)解:(1)设经过x秒,点A,B之间的距离等于3个单位长度,
则:|(﹣3+x)﹣(12﹣2x)|=3,
解得:x=4或x=6,
答:经过4秒或6秒,点A,B之间的距离等于3个单位长度;
(2)设经过x秒,点A,B到原点距离之和为y,
则y=|﹣3+x|+|12﹣2x|,
当x≤3时,y=|﹣3+x|+|12﹣2x|=3﹣x+12﹣2x=﹣3x+15,
当x=3时,y值最小,为6,
当3<x≤6时,y=|﹣3+x|+|12﹣2x|=﹣3+x+12﹣2x=﹣x+9,
当x=6时,y值最小,为3,
当x>6时,y=|﹣3+x|+|12﹣2x|=﹣3+x﹣12+2x=3x﹣15,
当x=6时,y有极小值,为3,
综上所述,点A,B到原点距离之和的最小值为3.
22.(10分)(1)证明:如图,连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵BC=CD,
∴∠DAC=∠BAC,
∴∠OCA=∠DAC,
∴OC∥AF,
∵EH平分∠FEG,
∴∠FEH=∠GEH,
∵∠GEH=∠H+∠BAC,∠FEH=∠F+∠BAF,
∴2∠H+2∠BAC=∠F+∠BAF,
∴∠BAF=2∠BAC,
∴∠F=2∠H=90°,
∴∠OCE=∠F=90°,
即OC⊥EF,
∵OC是半径,
∴EF是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,即∠OCB+∠BCE=90°,
∴∠OBC+∠BAC=90°,
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠BCE=∠EAC,
∵∠CEB=∠CAE,
∴△BCE∽△CAE,
∴,
∴CE2=BE AE,即16=2AE,
解得AE=8,
∴AB=8﹣2=6,
在Rt△ABC中,AB=6,,
∴BC,AC,
∵∠F=∠ACB=90°,∠FAC=∠BAC,
∴△FAC∽△CAB,
∴,
∴AF.
23.(10分)(1)证明:设CD与EF相交于点M,
∵四边形ABCD为菱形,∴BC﹣=DC,∠BCE=∠DCE,AB∥CD,
∵∠ABC=60°,
∴∠DCF=60°,
在△BCE和△DCE中,
,
∴△BCE≌△DCE(SAS),
∴∠CBE=∠CDE,BE=DE,
∵∠DMF=∠DEF+∠CDE=∠DCF+∠CFE,
又∵∠DEF=∠DCF=60°,
∴∠CDE=∠CFE,
∴∠CBE=∠CFE,
∴BE=EF;
(2)解:过点E作EN⊥BC于N,
则∠ENC=90°,
∵BE=EF,
∴BF=2BN,
∵四边形ABCD为菱形,∠ABC=60°,
∴ВС=АВ=10cm,∠АСВ=∠BСD=60°,即∠ECN=60°,
∵CE=2x cm,
∴EN=CE sin60°=2x x(cm),CN=CE cos60°=2x x(cm),
∴BN=BC﹣CN=10﹣x(cm),
∴BF=2(10﹣x)cm,
∴уВF ЕN2(10﹣х)хх2+10х,
∵0<2x≤10,
∴0<x≤5,
∴yх2+10х(0<x≤5);
(3)解:∵BE=DE,BE=EF,
∴DE=EF,
∵∠DEF=60°,
∴△DEF为等边三角形,
∴DE=DF﹣EF,
∴BE=DF,
∴线段DF的长度最短,即BE的长度最短,当BE⊥AC时,BE取最短,如图,
∵四边形 ABCD是菱形,
∴АВ=ВС,
∵∠ABC=60°,
∴△ABC为等边三角形,
∴AE=AB=AC=10cm,
∵BE⊥AC,
∴CEAC=5cm,
∴x,
∴当x时,线段DF的长度最短.
24.(12分)解:(1)∵y=x2+bx+c(b<0)与x轴交点的坐标分别为(x1,0),(x2,0),且x1<x2,
∴x1+x2=﹣b,且抛物线开口向上,
∵ 与x轴交点的坐标分别为(x3,0),(x4,0),且x1<x4,
即y=x2+bx+c(b<0)向上平移1个单位,
∴x1<x3<x4<x2,且x1+x4=﹣b,
∴①x1+x2=x1+x4;
∵x2﹣x1>x4﹣x3
∴x2﹣x4>x1﹣x3,即②x1﹣x5<x2﹣x4;
∴x1+x3>x1+x4,即③x2+x3>x1+x4,
故答案为:=;<;>;
(2)∵x1=1,2<x2<3,
∴3<x2+x1<4
∴3<﹣b<4,
∴﹣4<b<﹣3;
(3)抛物线y=x2+bx+c(b<0)顶点坐标为,对称轴为直线,
当x=0时,y=c;
当x=1时,y=1+b+c;
①当在 x=0 取得最大值,在x=1取得最小值时,有,
解得;
②当在x=0取得最大值,在顶点取得最小值时,
有,
解得(舍去)或;
③当在x=1取得最大值,在顶点取得最小值时,
有,
解得(舍去)或,
综上所述,b的值为或或.
(
1
/
35
)
同课章节目录
