2023--2024学年人教版八年级上册11.2 与三角形有关的角分类训练(含答案)
文档属性
| 名称 | 2023--2024学年人教版八年级上册11.2 与三角形有关的角分类训练(含答案) | 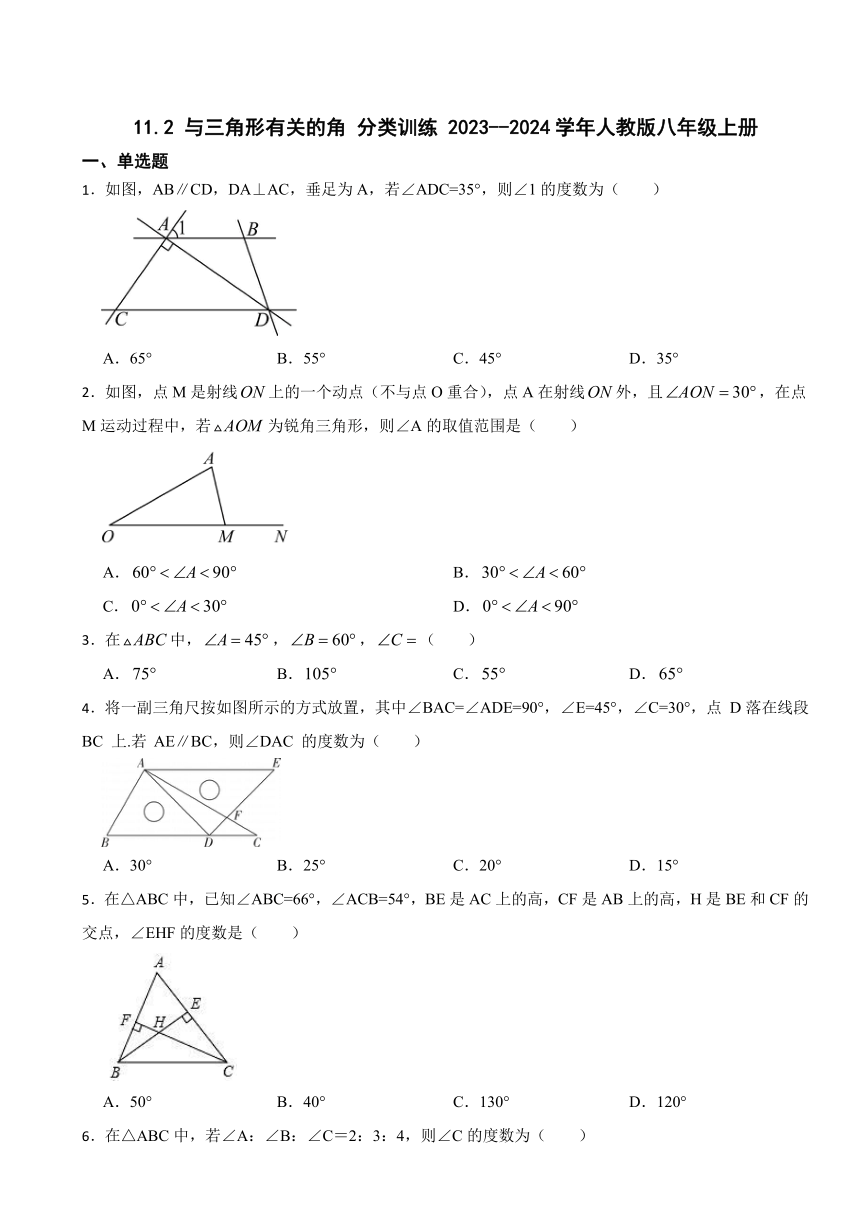 | |
| 格式 | docx | ||
| 文件大小 | 419.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 14:49:06 | ||
图片预览



文档简介
11.2 与三角形有关的角 分类训练 2023--2024学年人教版八年级上册
一、单选题
1.如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )
A.65° B.55° C.45° D.35°
2.如图,点M是射线上的一个动点(不与点O重合),点A在射线外,且,在点M运动过程中,若为锐角三角形,则∠A的取值范围是( )
A. B.
C. D.
3.在中,,,( )
A. B. C. D.
4.将一副三角尺按如图所示的方式放置,其中∠BAC=∠ADE=90°,∠E=45°,∠C=30°,点 D落在线段BC 上.若 AE∥BC,则∠DAC 的度数为( )
A.30° B.25° C.20° D.15°
5.在△ABC中,已知∠ABC=66°,∠ACB=54°,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,∠EHF的度数是( )
A.50° B.40° C.130° D.120°
6.在△ABC中,若∠A:∠B:∠C=2:3:4,则∠C的度数为( )
A.80° B.70° C.60° D.50°
7.如图,AB∥CD,∠E+∠F=85°,则∠A+∠C=( )
A.85° B.105° C.115° D.95°
8.一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D,点E,另一边与三角板的两直角边分别交于点F,点A,且∠CDE=40°,那么∠BAF的大小为( )
A.40° B.45° C.50° D.10°
9.如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°—∠ABD;④∠BDC=∠BAC,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
10.在三角形纸片中,,点D为边上靠近点C处一定点,点E为边上一动点,沿折叠三角形纸片,点C落在点处,①如图1,当点落在边上时,;②如图2,当点落在内部时,;③如图3,当点落在上方时,;④当时,或,以上结论正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.如果一个三角形三个内角的度数之比为3∶4∶5,那么此三角形的最大外角等于 度.
12.如图,将沿直线BA向左平移后,到达的位置,若,,则 .
13.如图, ABC中,CD是∠ACD的平分线,点E在AC上,,则∠EDC的度数为 .
14.如图,直线AB∥EF,点C是直线AB上一点,点D是直线AB外一点,若∠BCD=95°,∠CDE=25°,则∠DEF= 度.
15.如图,直线AB、CD相交于点O,∠BOC=α,点F在直线AB上且在点O的右侧,点E在射线OC上,连接EF,直线EM、FN交于点G.若∠MEF=n∠CEF,∠NFE=(1﹣2n)∠AFE,且∠EGF的度数与∠AFE的度数无关,则∠EGF= .(用含有α的代数式表示)
三、解答题
16.如图,在中,,平分.求和的度数.
17.如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠EAB=110°,∠C=60°,点D在GH上,求∠BDC的度数.
18.如图,已知F是ED上一点,∠D=∠A+∠EFA,求证:AB∥CD.
19.如图,在△ABC中,AD是高,AE,BF是角平分线,它们相交于点O,∠BAC=50°,∠C=60°,求∠DAC和∠BOA的度数.
20.如图,在 中, 于点 , 平分 ,若 , ,求 的度数?
21. 将一块直角三角板放置在锐角上,使得该三角板的两条直角边、恰好分别经过点、.
(1)如图,若时,点在内,则 度, 度, 度;
(2)如图,改变直角三角板的位置,使点在内,请探究与之间存在怎样的数量关系,并验证你的结论.
(3)如图,改变直角三角板的位置,使点在外,且在边的左侧,直接写出、、三者之间存在的数量关系.
22.已知 ,射线 分别和直线 交于点 ,射线 分别和直线 交于点 .点 在 上( 点与 三点不重合).连接 .请你根据题意画出图形并用等式直接写出 、 、 之间的数量关系.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】A
4.【答案】D
5.【答案】D
6.【答案】A
7.【答案】D
8.【答案】D
9.【答案】C
10.【答案】D
11.【答案】135
12.【答案】30°
13.【答案】25°
14.【答案】120
15.【答案】α#
16.【答案】;
17.【答案】解:∵EF∥GH,
∴∠CBG=∠EAB,
∵∠EAB=110°,
∴∠CBG=110°,
∴∠CBD=180°﹣∠CBG=70°,
在△BCD中,∵∠C=60°,
∴∠BDC=180°﹣∠C﹣∠CBD=180°﹣60°﹣70°=50°,
即:∠BDC的度数为50°.
18.【答案】证明:∵∠BEF是△AEF的外角,∴∠BEF=∠A+∠EFA,
又∠D=∠A+∠EFA,∴∠BEF=∠D,
∴AB∥CD.
19.【答案】解:∵在△ABC中,AD是高,
∴∠ADC=90°,
∵在△ACD中,∠C=60°,
∴∠DAC=90°-60°=30°,
∵在△ABC中,∠C=60°,∠BAC=50°,
∴∠ABC=70°,
∵在△ABC中,AE,BF分别是∠BAC和∠ABC的角平分线,
∴∠EAC=∠BAC=25°,∠FBC=∠ABC=35°,
∴∠BOA=∠BEA+∠FBC=∠C+∠EAC+∠FBC=60°+25°+35°=120°.
20.【答案】解:∵ 于 ,∴ ,
∵ 平分 ,∴ ,
而 ,∴ ,
∵ ,
∴ ,
,
若 , ,则 .
21.【答案】(1)140;90;50
(2)解:与之间的数量关系为:证明如下:
在中,
在中,
.
.
(3).
22.【答案】解:设∠BDP=α、∠ACP=β、∠CPD=γ.
当点 在线段 上时,∠γ=α+∠β,即 .
理由:过点P作PF∥l1(如图1),
∵l1∥l2,
∴PF∥l2,
∴∠α=∠DPF,∠β=∠CPF,
∴∠γ=∠DPF+∠CPF=α+∠β;
当点P在MB上运动时,∠β=∠γ+∠α,即 .
理由:如图2,
∵l1∥l2,
∴∠β=∠CFD,
∵∠CFD是△DFP的外角,
∴∠CFD=∠α+∠γ
∴∠β=∠γ+∠α;
同理可得,当点P在AN上运动时,∠α=∠γ+∠β,即 .
一、单选题
1.如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )
A.65° B.55° C.45° D.35°
2.如图,点M是射线上的一个动点(不与点O重合),点A在射线外,且,在点M运动过程中,若为锐角三角形,则∠A的取值范围是( )
A. B.
C. D.
3.在中,,,( )
A. B. C. D.
4.将一副三角尺按如图所示的方式放置,其中∠BAC=∠ADE=90°,∠E=45°,∠C=30°,点 D落在线段BC 上.若 AE∥BC,则∠DAC 的度数为( )
A.30° B.25° C.20° D.15°
5.在△ABC中,已知∠ABC=66°,∠ACB=54°,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,∠EHF的度数是( )
A.50° B.40° C.130° D.120°
6.在△ABC中,若∠A:∠B:∠C=2:3:4,则∠C的度数为( )
A.80° B.70° C.60° D.50°
7.如图,AB∥CD,∠E+∠F=85°,则∠A+∠C=( )
A.85° B.105° C.115° D.95°
8.一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D,点E,另一边与三角板的两直角边分别交于点F,点A,且∠CDE=40°,那么∠BAF的大小为( )
A.40° B.45° C.50° D.10°
9.如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°—∠ABD;④∠BDC=∠BAC,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
10.在三角形纸片中,,点D为边上靠近点C处一定点,点E为边上一动点,沿折叠三角形纸片,点C落在点处,①如图1,当点落在边上时,;②如图2,当点落在内部时,;③如图3,当点落在上方时,;④当时,或,以上结论正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.如果一个三角形三个内角的度数之比为3∶4∶5,那么此三角形的最大外角等于 度.
12.如图,将沿直线BA向左平移后,到达的位置,若,,则 .
13.如图, ABC中,CD是∠ACD的平分线,点E在AC上,,则∠EDC的度数为 .
14.如图,直线AB∥EF,点C是直线AB上一点,点D是直线AB外一点,若∠BCD=95°,∠CDE=25°,则∠DEF= 度.
15.如图,直线AB、CD相交于点O,∠BOC=α,点F在直线AB上且在点O的右侧,点E在射线OC上,连接EF,直线EM、FN交于点G.若∠MEF=n∠CEF,∠NFE=(1﹣2n)∠AFE,且∠EGF的度数与∠AFE的度数无关,则∠EGF= .(用含有α的代数式表示)
三、解答题
16.如图,在中,,平分.求和的度数.
17.如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠EAB=110°,∠C=60°,点D在GH上,求∠BDC的度数.
18.如图,已知F是ED上一点,∠D=∠A+∠EFA,求证:AB∥CD.
19.如图,在△ABC中,AD是高,AE,BF是角平分线,它们相交于点O,∠BAC=50°,∠C=60°,求∠DAC和∠BOA的度数.
20.如图,在 中, 于点 , 平分 ,若 , ,求 的度数?
21. 将一块直角三角板放置在锐角上,使得该三角板的两条直角边、恰好分别经过点、.
(1)如图,若时,点在内,则 度, 度, 度;
(2)如图,改变直角三角板的位置,使点在内,请探究与之间存在怎样的数量关系,并验证你的结论.
(3)如图,改变直角三角板的位置,使点在外,且在边的左侧,直接写出、、三者之间存在的数量关系.
22.已知 ,射线 分别和直线 交于点 ,射线 分别和直线 交于点 .点 在 上( 点与 三点不重合).连接 .请你根据题意画出图形并用等式直接写出 、 、 之间的数量关系.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】A
4.【答案】D
5.【答案】D
6.【答案】A
7.【答案】D
8.【答案】D
9.【答案】C
10.【答案】D
11.【答案】135
12.【答案】30°
13.【答案】25°
14.【答案】120
15.【答案】α#
16.【答案】;
17.【答案】解:∵EF∥GH,
∴∠CBG=∠EAB,
∵∠EAB=110°,
∴∠CBG=110°,
∴∠CBD=180°﹣∠CBG=70°,
在△BCD中,∵∠C=60°,
∴∠BDC=180°﹣∠C﹣∠CBD=180°﹣60°﹣70°=50°,
即:∠BDC的度数为50°.
18.【答案】证明:∵∠BEF是△AEF的外角,∴∠BEF=∠A+∠EFA,
又∠D=∠A+∠EFA,∴∠BEF=∠D,
∴AB∥CD.
19.【答案】解:∵在△ABC中,AD是高,
∴∠ADC=90°,
∵在△ACD中,∠C=60°,
∴∠DAC=90°-60°=30°,
∵在△ABC中,∠C=60°,∠BAC=50°,
∴∠ABC=70°,
∵在△ABC中,AE,BF分别是∠BAC和∠ABC的角平分线,
∴∠EAC=∠BAC=25°,∠FBC=∠ABC=35°,
∴∠BOA=∠BEA+∠FBC=∠C+∠EAC+∠FBC=60°+25°+35°=120°.
20.【答案】解:∵ 于 ,∴ ,
∵ 平分 ,∴ ,
而 ,∴ ,
∵ ,
∴ ,
,
若 , ,则 .
21.【答案】(1)140;90;50
(2)解:与之间的数量关系为:证明如下:
在中,
在中,
.
.
(3).
22.【答案】解:设∠BDP=α、∠ACP=β、∠CPD=γ.
当点 在线段 上时,∠γ=α+∠β,即 .
理由:过点P作PF∥l1(如图1),
∵l1∥l2,
∴PF∥l2,
∴∠α=∠DPF,∠β=∠CPF,
∴∠γ=∠DPF+∠CPF=α+∠β;
当点P在MB上运动时,∠β=∠γ+∠α,即 .
理由:如图2,
∵l1∥l2,
∴∠β=∠CFD,
∵∠CFD是△DFP的外角,
∴∠CFD=∠α+∠γ
∴∠β=∠γ+∠α;
同理可得,当点P在AN上运动时,∠α=∠γ+∠β,即 .
