8.1基本立体图形 练习(含解析)
文档属性
| 名称 | 8.1基本立体图形 练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 371.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 16:00:46 | ||
图片预览


文档简介
立体几何初步
8.1 基本立体图形
一、单选题
1.某圆锥的侧面展开图扇形的弧长为,扇形的半径为5,则圆锥的体积为( )
A. B.75 C. D.
2.轴截面为正方形的圆柱内接于球,则它们的表面积之比是( )
A.1:2 B.2:1 C.3:4 D.4:3
3.已知某圆锥的侧面展开图为半圆,该圆锥的体积为,则该圆锥的表面积为( )
A.27π B. C. D.16π
4.圆锥的轴截面是边长为4的正三角形,则该圆锥的表面积为( )
A. B.9π C.12π D.10π
5.我国古代《九章算术》中将上,下两面为平行矩形的六面体称为刍童.如图的刍童 有外接球,且 , , , ,平面 与平面 间的距离为1,则该刍童外接球的体积为
A. B. C. D.
6.如图,在正三角形ABC中, D,E,F分别为AB,BC,AC的中点,G,H,I分别为DE,FC,EF的中点,将△ABC沿DE,EF,DF折成三棱锥,则异面直线BG与IH所成的角为( )
A. B. C. D.
7.如图所示,正方体ABCD﹣A1B1C1D1的棱长为1,BD∩AC=0,M是线段D1O上的动点,过点M做平面ACD1的垂线交平面A1B1C1D1于点N,则点N到点A距离的最小值为( )
A. B. C. D.1
8.若圆锥的侧面展开图是圆心角为120°、半径为l的扇形,则这个圆锥的表面积与侧面积的比是( )
A.4:3 B.2:1 C.5:3 D.3:2
二、多选题
9.用一个平面去截正方体,截面的形状不可能是( )
A.直角三角形 B.等腰梯形 C.正五边形 D.正六边形
10.下列说法中不正确的是( )
A.棱柱的侧面可以是三角形
B.正方体和长方体都是特殊的四棱柱
C.所有几何体的表面都能展开成平面图形
D.棱柱的各条棱都相等
11.下列说法正确的是( )
A.棱柱的侧面一定是矩形
B.三个平面至多将空间分为7个部分
C.圆台可由直角梯形以高所在直线为旋转轴旋转一周形成
D.任意五棱锥都可以分成3个三棱锥
12.在棱长为1的正方体中,M是线段上一个动点,则结论正确的是( )
A.直线垂直于直线
B.存在点M使得二面角为的二面角
C.存在点M使得异面直线与所成角为
D.三棱锥的体积为
三、填空题
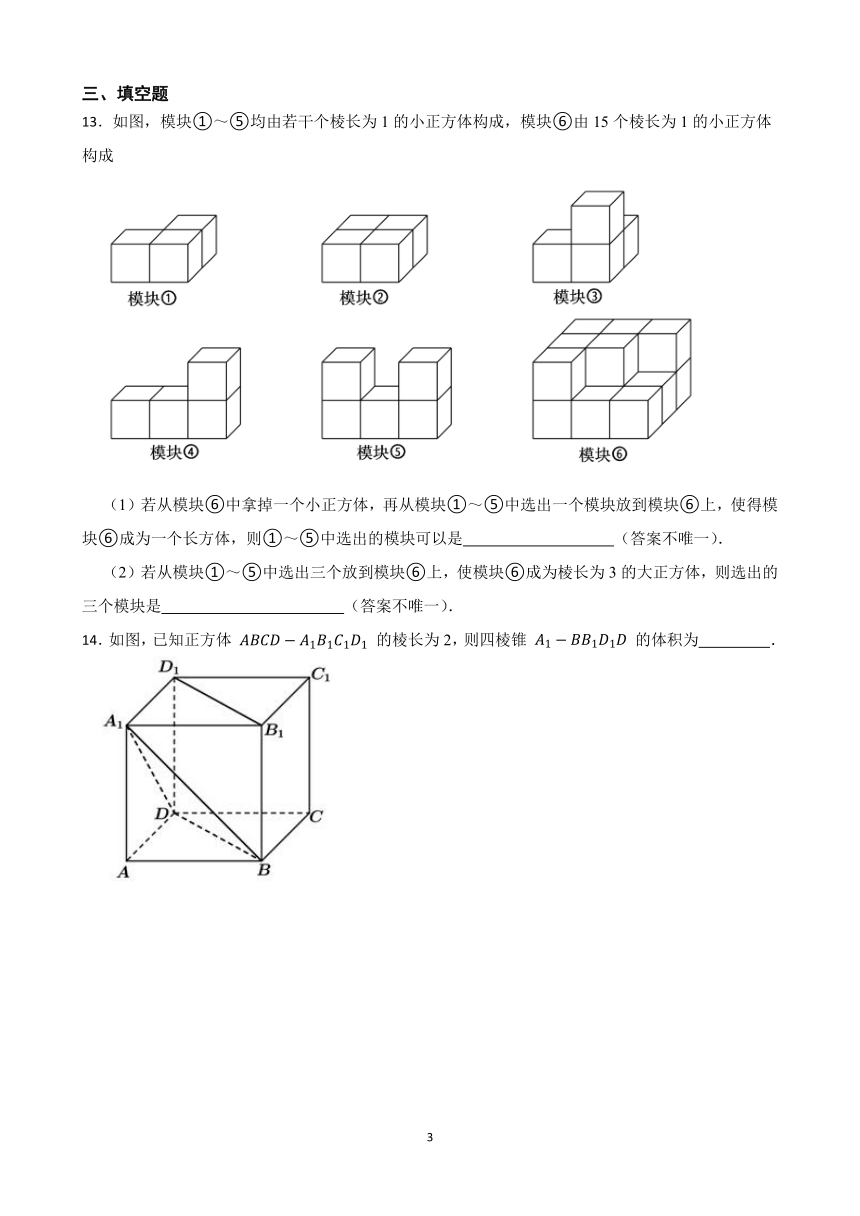
13.如图,模块①~⑤均由若干个棱长为1的小正方体构成,模块⑥由15个棱长为1的小正方体构成
(1)若从模块⑥中拿掉一个小正方体,再从模块①~⑤中选出一个模块放到模块⑥上,使得模块⑥成为一个长方体,则①~⑤中选出的模块可以是 (答案不唯一).
(2)若从模块①~⑤中选出三个放到模块⑥上,使模块⑥成为棱长为3的大正方体,则选出的三个模块是 (答案不唯一).
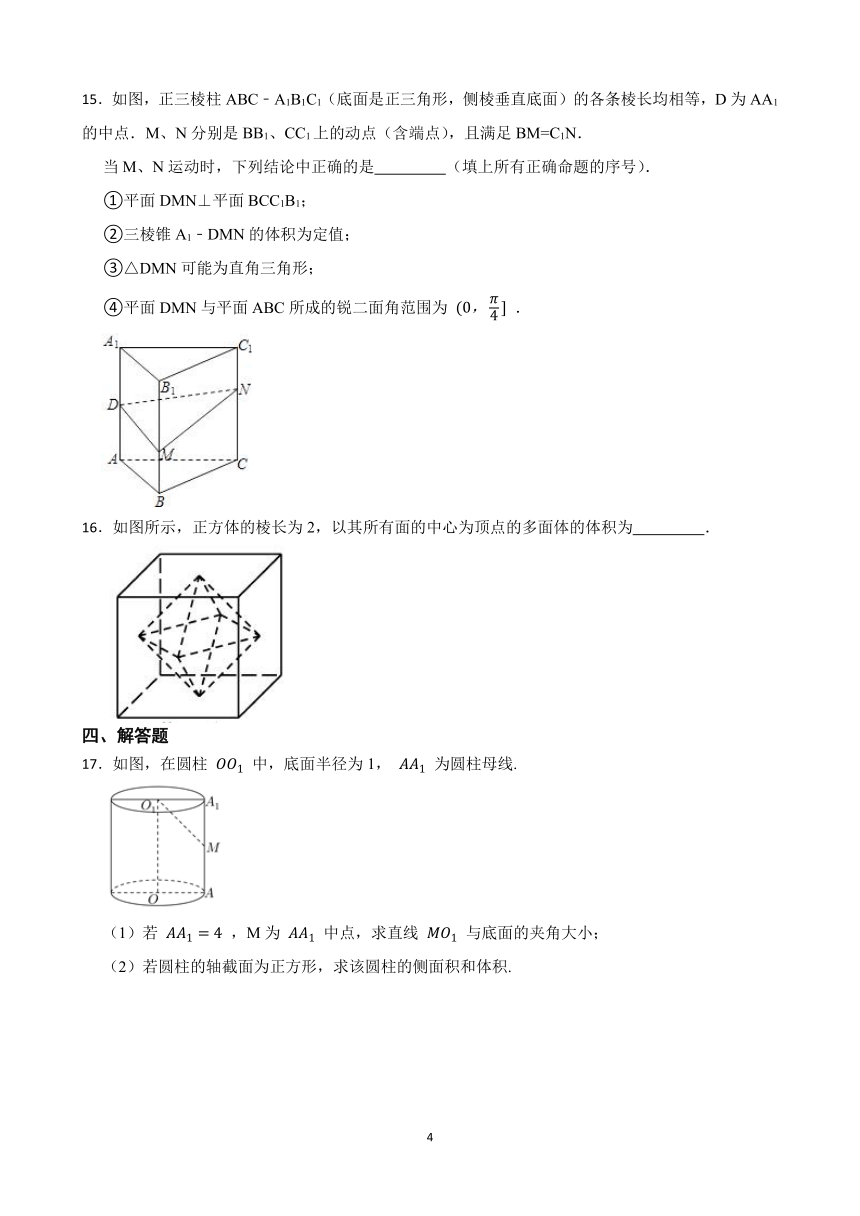
14.如图,已知正方体 的棱长为2,则四棱锥 的体积为 .
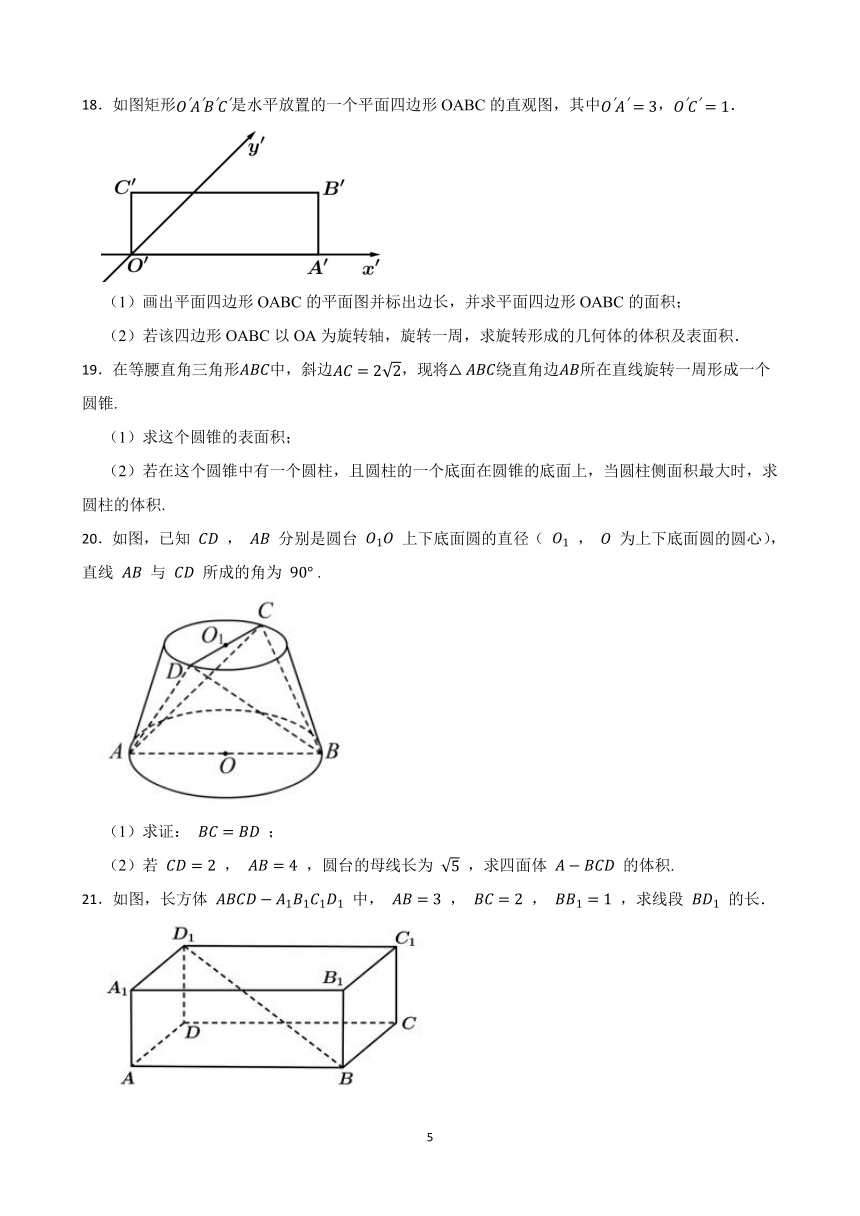
15.如图,正三棱柱ABC﹣A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.
当M、N运动时,下列结论中正确的是 (填上所有正确命题的序号).
①平面DMN⊥平面BCC1B1;
②三棱锥A1﹣DMN的体积为定值;
③△DMN可能为直角三角形;
④平面DMN与平面ABC所成的锐二面角范围为 .
16.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 .
四、解答题
17.如图,在圆柱 中,底面半径为1, 为圆柱母线.
(1)若 ,M为 中点,求直线 与底面的夹角大小;
(2)若圆柱的轴截面为正方形,求该圆柱的侧面积和体积.
18.如图矩形是水平放置的一个平面四边形OABC的直观图,其中,.
(1)画出平面四边形OABC的平面图并标出边长,并求平面四边形OABC的面积;
(2)若该四边形OABC以OA为旋转轴,旋转一周,求旋转形成的几何体的体积及表面积.
19.在等腰直角三角形中,斜边,现将绕直角边所在直线旋转一周形成一个圆锥.
(1)求这个圆锥的表面积;
(2)若在这个圆锥中有一个圆柱,且圆柱的一个底面在圆锥的底面上,当圆柱侧面积最大时,求圆柱的体积.
20.如图,已知 , 分别是圆台 上下底面圆的直径( , 为上下底面圆的圆心),直线 与 所成的角为 .
(1)求证: ;
(2)若 , ,圆台的母线长为 ,求四面体 的体积.
21.如图,长方体 中, , , ,求线段 的长.
22.如图,在正方体ABCD﹣A1B1C1D1中,AB=2,点E是BC的中点.
(1)求线段DE的长;
(2)求直线A1E与平面ADD1A1所成角的正弦值.
答案解析部分
1.【答案】D
【解析】【解答】设底面圆的半径为,则,解得:,
设圆锥的高为,则,
则圆锥的体积为.
故答案为:D
2.【答案】C
【解析】【解答】轴截面如下图,
四边形ABCD为正方形,设圆柱底面圆直径,则球直径,故圆柱表面积为,球表面积为,故它们的表面积之比为3:4。
故答案为:C
3.【答案】A
【解析】【解答】设圆锥底面半径为r,母线长为l,则,所以,所以圆锥的高为,
所以,解得,故其表面积。
故答案为:A.
4.【答案】C
【解析】【解答】圆锥的轴截面是边长为4的正三角形,
则母线长为 ,底面圆半径为 ,
该圆锥的表面积为 ,
故答案为:C.
5.【答案】C
【解析】【解答】解:假设O为刍童外接球的球心,连接HF, EG交于点O1,连接AC,DB交于点O2,
由球的几何性质可知O,O1,O2在同一条直线上,
由题意可知OO1⊥平面ABCD,OO1⊥平面EFGH , O1O2=1.
设OO2=r ,
在Rt△OGO1中,OG2=OO12+O1G2,
在矩形EFGH中,
在Rt△OBO2中,OB2=OO22+O2B2,
在矩形ABCD中,
,
∴
设外接球的半径为OG=OB=R,
∴
解得r=1
则
则R=3
则
故答案为:C
6.【答案】A
【解析】【分析】先画出折叠后的直观图画出来,再将两条异面直线平移到同一个平面内,最后在平面三角形中计算此角即可
【解答】将△ABC沿DE,EF,DF折成三棱锥如图
设顶点为P
由三角形中位线定理,IH∥PE,
∴∠EPG就是异面直线BG与IH所成的角
在三角形PED中,
∴∠DPG=∠EPG=
故答案选 A
7.【答案】B
【解析】【解答】解:∵平面ACD1⊥平面BDD1B1,又MN⊥平面ACD1,
∴MN 平面BDD1B1,∴N∈B1D1
过N作NG⊥A1B1,交A1B1于G,将平面A1B1C1D1展开,如图:
设NG=x,(0≤x≤1),
∴AN= = = ≥ ,
当x= 时最小.
故选B.
8.【答案】A
【解析】【解答】解:圆锥的侧面积=π×12× =
圆锥的底面半径=2π×1× ÷2π= ,
圆锥的底面积= = ,
圆锥的表面积=侧面积+底面积= ,
∴这个圆锥的表面积与侧面积的比=4:3.
故选A
9.【答案】A,C
【解析】【解答】截面为六边形时,可能出现正六边形,
当截面为五边形时,假若截面是正五边形,则截面中的截线必然分别在5个面内,由于正方体有6个面,分成两两平行的三对,故必然有一对平行面中有两条截线,而根据面面平行的性质定理,可知这两条截线互相平行,但正五边形的边中是不可能有平行的边的,故截面的形状不可能是正五边形;
截面为四边形时,可能出现矩形,平行四边形,等腰梯形,但不可能出现直角梯形;
当截面为三角形时,可能出现正三角形,但不可能出现直角三角形;
故答案为:AC.
10.【答案】A,C,D
【解析】【解答】解:棱柱的侧面都是四边形,A不正确;
正方体和长方体都是特殊的四棱柱,B符合题意;
不是所有几何体的表面都能展开成平面图形,球不能展开成平面图形,C不正确;
棱柱的各条棱并不是都相等,应该为棱柱的侧棱都相等,所以D不正确.
故答案为:ACD.
11.【答案】C,D
【解析】【解答】对于A选项,斜棱柱的侧面不一定是矩形,A不符合题意;
对于B选项,若三个平面两两垂直,则这三个平面可将空间分为8个部分,B不符合题意;
对于C选项,圆台可由直角梯形以高所在直线为旋转轴旋转一周形成,C对;
对于D选项,一个五边形可分为三个三角形,所以,任意五棱锥都可以分成3个三棱锥,D对.
故答案为:CD.
12.【答案】A,B,C
【解析】【解答】由题意可知,,,∴,A符合题意;
当M为中点时,二面角的平面角为,所以B符合题意;
异面直线与所成的角可转化为直线与所成角,
为正三角形,当M为中点时,,C符合题意;
三棱锥的体积为,D不符合题意.
故答案为:ABC.
13.【答案】(1)②(或③或④)
(2)①③⑤(或②③④)
【解析】【解答】(1)由已知条件可知,①~⑤中选出一个模块可以是②,也可以是③,也可以是④.
(2)以②③④为例,中间层用③补齐,最上层用②④,
还可以是①③⑤,中间层用③补齐,最上层用①⑤,
故答案为:②(或③或④),①③⑤(或②③④).
14.【答案】
【解析】【解答】如图所示:
连接 交 于点E,则 ,又 ,
所以 平面 ,
所以 为四棱锥 的高,且 ,
矩形 的长和宽分别为 ,2,
故 。
故答案为: 。
15.【答案】①②④
【解析】【解答】解:如图,
当M、N分别在BB1、CC1上运动时,若满足BM=C1N,则线段MN必过正方形BCC1B1的中心O,而DO⊥平面BCC1B1,∴平面DMN⊥平面BCC1B1,①正确;
当M、N分别在BB1、CC1上运动时,△A1DM的面积不变,N到平面A1DM的距离不变,∴棱锥N﹣A1DM的体积不变,即三棱锥A1﹣DMN的体积为定值,②正确;
若△DMN为直角三角形,则必是以∠MDN为直角的直角三角形,但MN的最大值为BC1,而此时DM,DN的长大于BB1,∴△DMN不可能为直角三角形,③错误;
当M、N分别为BB1,CC1中点时,平面DMN与平面ABC所成的角为0,当M与B重合,N与C1重合时,平面DMN与平面ABC所成的锐二面角最大,为∠C1BC,等于 .
∴平面DMN与平面ABC所成的锐二面角范围为(0, ],④正确,
∴正确的是①②④.
故答案为:①②④.
16.【答案】
【解析】【解答】解:由图可知,该多面体为两个全等正四棱锥的组合体,正四棱锥的高为1,底面正方形的边长等于 ,所以该多面体的体积为
17.【答案】(1)根据直线与平面所成角的定义,易知 直线MO1与底面的夹角为∠MO1A1
则由题意得,
则∠MO1A1= ;
(2)设圆柱的底面圆的半径为r,高为h,
则因为圆柱的轴截面为正方形,
所以h=2r=2
所以圆柱的侧面积为
圆柱的体积为
18.【答案】(1)解:平面四边形的平面图如下图所示:
由直观图可知菱形的高为:,
所以面积为;
(2)解:旋转而成的几何体如下图所示:
该几何体可以看成圆柱挖去一个同底的圆锥再加上一个同底的圆锥,
由(1)可知圆柱的底面圆半径为,母线长为,
所以体积;
所以表面积.
19.【答案】(1)解:在等腰直角三角形中,斜边,所以,且.
所以圆锥的表面积.
(2)解:设圆柱的底面半径为r,高为x,根据题意,画出圆锥的轴截面如图所示,
由图可知,且.
所以圆柱侧面积.
显然当时,圆柱侧面积取得最大值,最大值为,此时.
故圆柱的体积.
20.【答案】(1)证明:连接 , , ,
由圆台的性质可知: ,
因为直线 与 所成的角为 ,即 ,
又因为 ,所以 平面 ,所以 ,
又 是 的中点,所以 .
(2)由(1)可知 平面 ,
因为 , ,圆台的母线长为 ,所以圆台的高 ,
所以 的面积 ,
所以四面体 的体积 .
21.【答案】因为在长方体 中, , , ,
连接 ,在 中,有 ,
又因为在长方体 中, 平面 ,
所以 ,在 中,
.
22.【答案】(1)解:以D为原点, , , 方向为x轴,y轴,z轴,建立空间直角坐标系,
则D(0,0,0),E(1,2,0), =(1,2,0),
∴线段DE的长| |= = .
(2)解:∵A1(2,0,2),E(1,2,0),∴ =(﹣1,2,﹣2),
∵平面ADD1A1的一个法向量 =(0,2,0),
∴cos< , >= = = ,
∵直线A1E与平面ADD1A1所成角的正弦值等于 ,
∴直线A1E与平面ADD1A1所成角的正弦值为 .
8.1 基本立体图形
一、单选题
1.某圆锥的侧面展开图扇形的弧长为,扇形的半径为5,则圆锥的体积为( )
A. B.75 C. D.
2.轴截面为正方形的圆柱内接于球,则它们的表面积之比是( )
A.1:2 B.2:1 C.3:4 D.4:3
3.已知某圆锥的侧面展开图为半圆,该圆锥的体积为,则该圆锥的表面积为( )
A.27π B. C. D.16π
4.圆锥的轴截面是边长为4的正三角形,则该圆锥的表面积为( )
A. B.9π C.12π D.10π
5.我国古代《九章算术》中将上,下两面为平行矩形的六面体称为刍童.如图的刍童 有外接球,且 , , , ,平面 与平面 间的距离为1,则该刍童外接球的体积为
A. B. C. D.
6.如图,在正三角形ABC中, D,E,F分别为AB,BC,AC的中点,G,H,I分别为DE,FC,EF的中点,将△ABC沿DE,EF,DF折成三棱锥,则异面直线BG与IH所成的角为( )
A. B. C. D.
7.如图所示,正方体ABCD﹣A1B1C1D1的棱长为1,BD∩AC=0,M是线段D1O上的动点,过点M做平面ACD1的垂线交平面A1B1C1D1于点N,则点N到点A距离的最小值为( )
A. B. C. D.1
8.若圆锥的侧面展开图是圆心角为120°、半径为l的扇形,则这个圆锥的表面积与侧面积的比是( )
A.4:3 B.2:1 C.5:3 D.3:2
二、多选题
9.用一个平面去截正方体,截面的形状不可能是( )
A.直角三角形 B.等腰梯形 C.正五边形 D.正六边形
10.下列说法中不正确的是( )
A.棱柱的侧面可以是三角形
B.正方体和长方体都是特殊的四棱柱
C.所有几何体的表面都能展开成平面图形
D.棱柱的各条棱都相等
11.下列说法正确的是( )
A.棱柱的侧面一定是矩形
B.三个平面至多将空间分为7个部分
C.圆台可由直角梯形以高所在直线为旋转轴旋转一周形成
D.任意五棱锥都可以分成3个三棱锥
12.在棱长为1的正方体中,M是线段上一个动点,则结论正确的是( )
A.直线垂直于直线
B.存在点M使得二面角为的二面角
C.存在点M使得异面直线与所成角为
D.三棱锥的体积为
三、填空题
13.如图,模块①~⑤均由若干个棱长为1的小正方体构成,模块⑥由15个棱长为1的小正方体构成
(1)若从模块⑥中拿掉一个小正方体,再从模块①~⑤中选出一个模块放到模块⑥上,使得模块⑥成为一个长方体,则①~⑤中选出的模块可以是 (答案不唯一).
(2)若从模块①~⑤中选出三个放到模块⑥上,使模块⑥成为棱长为3的大正方体,则选出的三个模块是 (答案不唯一).
14.如图,已知正方体 的棱长为2,则四棱锥 的体积为 .
15.如图,正三棱柱ABC﹣A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.
当M、N运动时,下列结论中正确的是 (填上所有正确命题的序号).
①平面DMN⊥平面BCC1B1;
②三棱锥A1﹣DMN的体积为定值;
③△DMN可能为直角三角形;
④平面DMN与平面ABC所成的锐二面角范围为 .
16.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 .
四、解答题
17.如图,在圆柱 中,底面半径为1, 为圆柱母线.
(1)若 ,M为 中点,求直线 与底面的夹角大小;
(2)若圆柱的轴截面为正方形,求该圆柱的侧面积和体积.
18.如图矩形是水平放置的一个平面四边形OABC的直观图,其中,.
(1)画出平面四边形OABC的平面图并标出边长,并求平面四边形OABC的面积;
(2)若该四边形OABC以OA为旋转轴,旋转一周,求旋转形成的几何体的体积及表面积.
19.在等腰直角三角形中,斜边,现将绕直角边所在直线旋转一周形成一个圆锥.
(1)求这个圆锥的表面积;
(2)若在这个圆锥中有一个圆柱,且圆柱的一个底面在圆锥的底面上,当圆柱侧面积最大时,求圆柱的体积.
20.如图,已知 , 分别是圆台 上下底面圆的直径( , 为上下底面圆的圆心),直线 与 所成的角为 .
(1)求证: ;
(2)若 , ,圆台的母线长为 ,求四面体 的体积.
21.如图,长方体 中, , , ,求线段 的长.
22.如图,在正方体ABCD﹣A1B1C1D1中,AB=2,点E是BC的中点.
(1)求线段DE的长;
(2)求直线A1E与平面ADD1A1所成角的正弦值.
答案解析部分
1.【答案】D
【解析】【解答】设底面圆的半径为,则,解得:,
设圆锥的高为,则,
则圆锥的体积为.
故答案为:D
2.【答案】C
【解析】【解答】轴截面如下图,
四边形ABCD为正方形,设圆柱底面圆直径,则球直径,故圆柱表面积为,球表面积为,故它们的表面积之比为3:4。
故答案为:C
3.【答案】A
【解析】【解答】设圆锥底面半径为r,母线长为l,则,所以,所以圆锥的高为,
所以,解得,故其表面积。
故答案为:A.
4.【答案】C
【解析】【解答】圆锥的轴截面是边长为4的正三角形,
则母线长为 ,底面圆半径为 ,
该圆锥的表面积为 ,
故答案为:C.
5.【答案】C
【解析】【解答】解:假设O为刍童外接球的球心,连接HF, EG交于点O1,连接AC,DB交于点O2,
由球的几何性质可知O,O1,O2在同一条直线上,
由题意可知OO1⊥平面ABCD,OO1⊥平面EFGH , O1O2=1.
设OO2=r ,
在Rt△OGO1中,OG2=OO12+O1G2,
在矩形EFGH中,
在Rt△OBO2中,OB2=OO22+O2B2,
在矩形ABCD中,
,
∴
设外接球的半径为OG=OB=R,
∴
解得r=1
则
则R=3
则
故答案为:C
6.【答案】A
【解析】【分析】先画出折叠后的直观图画出来,再将两条异面直线平移到同一个平面内,最后在平面三角形中计算此角即可
【解答】将△ABC沿DE,EF,DF折成三棱锥如图
设顶点为P
由三角形中位线定理,IH∥PE,
∴∠EPG就是异面直线BG与IH所成的角
在三角形PED中,
∴∠DPG=∠EPG=
故答案选 A
7.【答案】B
【解析】【解答】解:∵平面ACD1⊥平面BDD1B1,又MN⊥平面ACD1,
∴MN 平面BDD1B1,∴N∈B1D1
过N作NG⊥A1B1,交A1B1于G,将平面A1B1C1D1展开,如图:
设NG=x,(0≤x≤1),
∴AN= = = ≥ ,
当x= 时最小.
故选B.
8.【答案】A
【解析】【解答】解:圆锥的侧面积=π×12× =
圆锥的底面半径=2π×1× ÷2π= ,
圆锥的底面积= = ,
圆锥的表面积=侧面积+底面积= ,
∴这个圆锥的表面积与侧面积的比=4:3.
故选A
9.【答案】A,C
【解析】【解答】截面为六边形时,可能出现正六边形,
当截面为五边形时,假若截面是正五边形,则截面中的截线必然分别在5个面内,由于正方体有6个面,分成两两平行的三对,故必然有一对平行面中有两条截线,而根据面面平行的性质定理,可知这两条截线互相平行,但正五边形的边中是不可能有平行的边的,故截面的形状不可能是正五边形;
截面为四边形时,可能出现矩形,平行四边形,等腰梯形,但不可能出现直角梯形;
当截面为三角形时,可能出现正三角形,但不可能出现直角三角形;
故答案为:AC.
10.【答案】A,C,D
【解析】【解答】解:棱柱的侧面都是四边形,A不正确;
正方体和长方体都是特殊的四棱柱,B符合题意;
不是所有几何体的表面都能展开成平面图形,球不能展开成平面图形,C不正确;
棱柱的各条棱并不是都相等,应该为棱柱的侧棱都相等,所以D不正确.
故答案为:ACD.
11.【答案】C,D
【解析】【解答】对于A选项,斜棱柱的侧面不一定是矩形,A不符合题意;
对于B选项,若三个平面两两垂直,则这三个平面可将空间分为8个部分,B不符合题意;
对于C选项,圆台可由直角梯形以高所在直线为旋转轴旋转一周形成,C对;
对于D选项,一个五边形可分为三个三角形,所以,任意五棱锥都可以分成3个三棱锥,D对.
故答案为:CD.
12.【答案】A,B,C
【解析】【解答】由题意可知,,,∴,A符合题意;
当M为中点时,二面角的平面角为,所以B符合题意;
异面直线与所成的角可转化为直线与所成角,
为正三角形,当M为中点时,,C符合题意;
三棱锥的体积为,D不符合题意.
故答案为:ABC.
13.【答案】(1)②(或③或④)
(2)①③⑤(或②③④)
【解析】【解答】(1)由已知条件可知,①~⑤中选出一个模块可以是②,也可以是③,也可以是④.
(2)以②③④为例,中间层用③补齐,最上层用②④,
还可以是①③⑤,中间层用③补齐,最上层用①⑤,
故答案为:②(或③或④),①③⑤(或②③④).
14.【答案】
【解析】【解答】如图所示:
连接 交 于点E,则 ,又 ,
所以 平面 ,
所以 为四棱锥 的高,且 ,
矩形 的长和宽分别为 ,2,
故 。
故答案为: 。
15.【答案】①②④
【解析】【解答】解:如图,
当M、N分别在BB1、CC1上运动时,若满足BM=C1N,则线段MN必过正方形BCC1B1的中心O,而DO⊥平面BCC1B1,∴平面DMN⊥平面BCC1B1,①正确;
当M、N分别在BB1、CC1上运动时,△A1DM的面积不变,N到平面A1DM的距离不变,∴棱锥N﹣A1DM的体积不变,即三棱锥A1﹣DMN的体积为定值,②正确;
若△DMN为直角三角形,则必是以∠MDN为直角的直角三角形,但MN的最大值为BC1,而此时DM,DN的长大于BB1,∴△DMN不可能为直角三角形,③错误;
当M、N分别为BB1,CC1中点时,平面DMN与平面ABC所成的角为0,当M与B重合,N与C1重合时,平面DMN与平面ABC所成的锐二面角最大,为∠C1BC,等于 .
∴平面DMN与平面ABC所成的锐二面角范围为(0, ],④正确,
∴正确的是①②④.
故答案为:①②④.
16.【答案】
【解析】【解答】解:由图可知,该多面体为两个全等正四棱锥的组合体,正四棱锥的高为1,底面正方形的边长等于 ,所以该多面体的体积为
17.【答案】(1)根据直线与平面所成角的定义,易知 直线MO1与底面的夹角为∠MO1A1
则由题意得,
则∠MO1A1= ;
(2)设圆柱的底面圆的半径为r,高为h,
则因为圆柱的轴截面为正方形,
所以h=2r=2
所以圆柱的侧面积为
圆柱的体积为
18.【答案】(1)解:平面四边形的平面图如下图所示:
由直观图可知菱形的高为:,
所以面积为;
(2)解:旋转而成的几何体如下图所示:
该几何体可以看成圆柱挖去一个同底的圆锥再加上一个同底的圆锥,
由(1)可知圆柱的底面圆半径为,母线长为,
所以体积;
所以表面积.
19.【答案】(1)解:在等腰直角三角形中,斜边,所以,且.
所以圆锥的表面积.
(2)解:设圆柱的底面半径为r,高为x,根据题意,画出圆锥的轴截面如图所示,
由图可知,且.
所以圆柱侧面积.
显然当时,圆柱侧面积取得最大值,最大值为,此时.
故圆柱的体积.
20.【答案】(1)证明:连接 , , ,
由圆台的性质可知: ,
因为直线 与 所成的角为 ,即 ,
又因为 ,所以 平面 ,所以 ,
又 是 的中点,所以 .
(2)由(1)可知 平面 ,
因为 , ,圆台的母线长为 ,所以圆台的高 ,
所以 的面积 ,
所以四面体 的体积 .
21.【答案】因为在长方体 中, , , ,
连接 ,在 中,有 ,
又因为在长方体 中, 平面 ,
所以 ,在 中,
.
22.【答案】(1)解:以D为原点, , , 方向为x轴,y轴,z轴,建立空间直角坐标系,
则D(0,0,0),E(1,2,0), =(1,2,0),
∴线段DE的长| |= = .
(2)解:∵A1(2,0,2),E(1,2,0),∴ =(﹣1,2,﹣2),
∵平面ADD1A1的一个法向量 =(0,2,0),
∴cos< , >= = = ,
∵直线A1E与平面ADD1A1所成角的正弦值等于 ,
∴直线A1E与平面ADD1A1所成角的正弦值为 .
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
