第三章 圆锥曲线的方程 单元测试(含解析)
文档属性
| 名称 | 第三章 圆锥曲线的方程 单元测试(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 61.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 16:13:15 | ||
图片预览




文档简介
第三章 圆锥曲线的方程 单元测试
一、单选题
1.(·内江模拟)以椭圆 的短轴的一个端点和两焦点为顶点的三角形为等边三角形,且椭圆 上的点到左焦点的最大距离为6,则椭圆 的标准方程为( )
A. B. C. D.
2.(高二上·深圳期中)已知椭圆 的左,右焦点分别为 ,P是C上一点, 垂直于x轴, ,则C的方程为( )
A. B. C. D.
3.(高二上·安阳期中)已知方程表示焦点在轴上的椭圆,则实数的取值范围是()
A. B. C. D.
4.(高一下·镇江期末)已知椭圆 ( )过点 ,则实数a的值为( )
A.3 B.4 C.5 D.6
5.(·钦州模拟)圆 上一动点 ,抛物线 上一动点 ,则 的最小值为( )
A. B.2 C.3 D.4
6.(·南通模拟)双曲线 ( , )的左 右焦点分别为 , ,若 上存在点 满足 ,则该双曲线的离心率为( )
A. B. C. D.
7.(高二上·沧县期中)已知双曲线 的中心在原点,焦点在坐标轴上,则“双曲线 的离心率 ”是“双曲线 的渐近线方程为 ”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
8.(高二上·建瓯月考)已知 是双曲线 上一点,双曲线的一条渐近线方程为 , , 分别是双曲线的左、右焦点,若 ,则 ( )
A.7 B.6 C.5 D.3
二、多选题
9.(高三上·汕头月考)椭圆 的焦距为 ,则 的值为( )
A.9 B.23 C. D.
10.(高二上·浙江期中)若方程表示的曲线为,则下列说法正确的有( )
A.若曲线为椭圆,则
B.若曲线为双曲线,则或
C.曲线不可能是圆
D.若曲线表示焦点在轴上的椭圆,则
11.(高二下·扬州月考)在平面直角坐标系 中,椭圆 上存在点 ,使得 ,其中 、 分别为椭圆的左、右焦点,则该椭圆的离心率可能为( )
A. B. C. D.
12.(·潍坊模拟)已知双曲线 的左,右焦点分别为 ,一条渐近线方程为 , 为 上一点,则以下说法正确的是( )
A. 的实轴长为 B. 的离心率为
C. D. 的焦距为
三、填空题
13.(高二上·西安期中)抛物线的焦点坐标为 .
14.(高二上·毕节期末)抛物线的焦点坐标为 .
15.(·湖北模拟)已知双曲线:,F是双曲线C的右焦点,点A是双曲线C的左支上的一点,点B为圆D:上一点,则的最小值为 .
16.(高二下·上海期末)如果曲线C上的动点P到定点 的距离存在最小值,则称此最小值为点 到曲线C的距离.若点 到圆 的距离等于它到直线 的距离,则点 的轨迹方程是 .
四、解答题
17.(高二上·河南月考)
(1)求经过点 且焦点在坐标轴上的椭圆的标准方程﹔
(2)求与双曲线 有公共的渐近线,且过点 的双曲线的标准方程.
18.(高二上·莆田期中)已知椭圆两焦点 、 且经过点
(1)求椭圆的标准方程;
(2)若点 是椭圆上的一个点,且 ,求 的面积.
19.(高二上·绥德月考)叙述抛物线的定义,并推导抛物线的一个标准方程.
20.(·湛江模拟)已知双曲线C: =1(a,b>0)的左、右焦点分别为F1(-c,0),F2(c,0),其中c>0, M(c,3)在C上,且C的离心率为2.
(1)求C的标准方程;
(2)若O为坐标原点,∠F1MF2的角平分线l与曲线D: =1的交点为P,Q,试判断OP与OQ是否垂直,并说明理由.
21.(高二上·宁波期中)已知椭圆 焦点为 ,且过点 ,椭圆第一象限上的一点 到两焦点 的距离之差为2.
(1)求椭圆的标准方程;
(2)求 的内切圆方程.
22.(高二上·南京月考)已知椭圆 : ,点 为椭圆短轴的上端点, 为椭圆上异于 点的任一点,若 点到 点距离的最大值仅在 点为短轴的另一端点时取到,则称此椭圆为“圆椭圆”.
(1)若 ,判断椭圆 是否为“圆椭圆”;
(2)若椭圆 是“圆椭圆”,求 的取值范围.
答案解析部分
1.【答案】C
【解析】【解答】解:由题意知:短轴端点与焦点形成等边三角形,则 ,
椭圆上的点到左焦点最大距离为6,即 ,
则 , , .
则椭圆的标准方程为: .
故答案为:C.
2.【答案】C
【解析】【解答】解:因为 垂直于x轴, ,
所以 ,
所以 ,则 ,
所以C的方程为 .
故答案为:C.
3.【答案】D
【解析】【解答】由题知: 表示焦点在 轴上的椭圆,
所以
,
解得 。
故答案为:D.
4.【答案】B
【解析】【解答】解:因为椭圆过 ,所以 , ,所以 ,
故答案为:B.
5.【答案】B
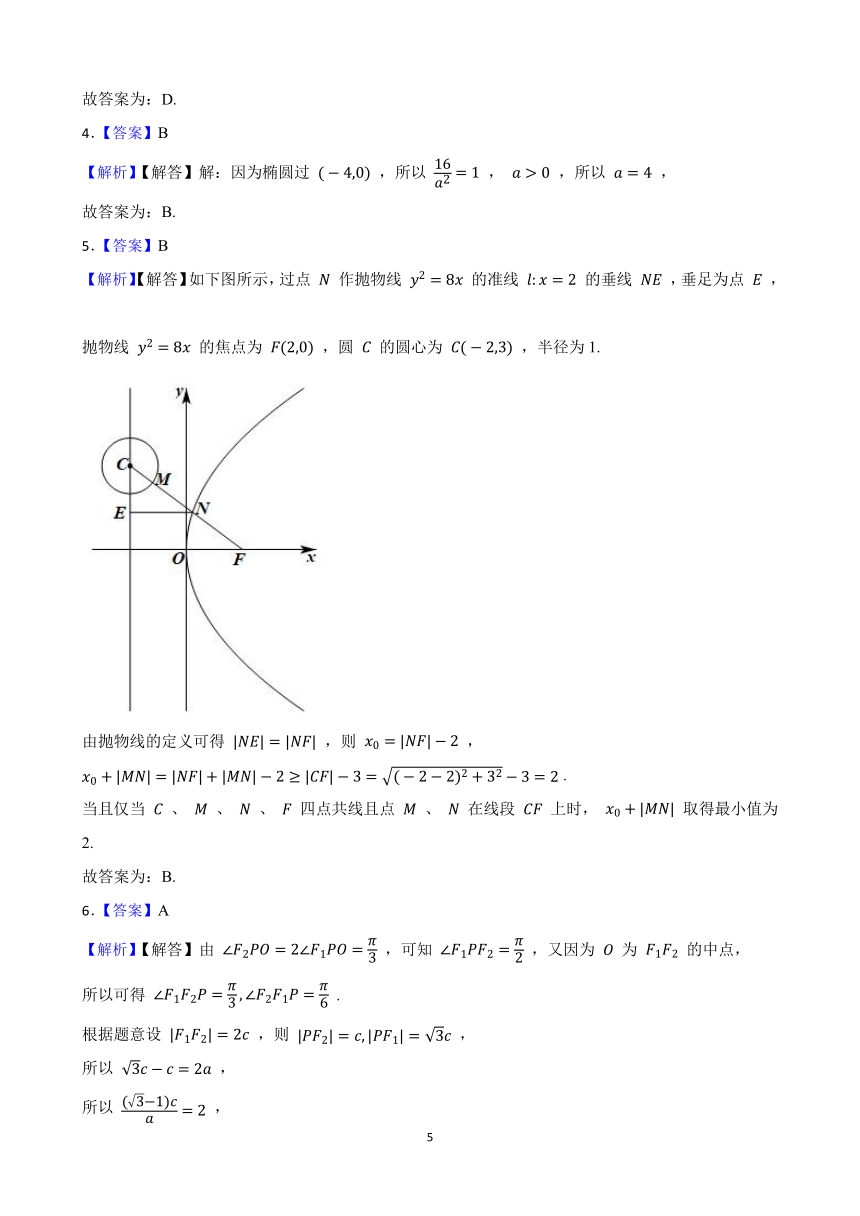
【解析】【解答】如下图所示,过点 作抛物线 的准线 的垂线 ,垂足为点 ,
抛物线 的焦点为 ,圆 的圆心为 ,半径为1.
由抛物线的定义可得 ,则 ,
.
当且仅当 、 、 、 四点共线且点 、 在线段 上时, 取得最小值为2.
故答案为:B.
6.【答案】A
【解析】【解答】由 ,可知 ,又因为 为 的中点,
所以可得 .
根据题意设 ,则 ,
所以 ,
所以 ,
则 。
故答案为:A.
7.【答案】D
【解析】【解答】因为双曲线 的渐近线方程为 ,所以双曲线 的离心率 或
双曲线 的离心率 时, ,所以双曲线 的渐近线方程为 或 ,
因此“双曲线 的离心率 ”是“双曲线 的渐近线方程为 ”的既不充分也不必要条件
故答案为:D
8.【答案】A
【解析】【解答】解:由双曲线的方程、渐近线的方程可得 , .由双曲线的定义可得 ,
, (舍去)
故答案为:A .
9.【答案】A,B
【解析】【解答】解:椭圆 的焦距为 ,即 得 .
依题意当焦点在 轴上时,则 ,解得 ;
当焦点在 轴上时,则 ,解得 ,
∴ 的值为9或23.
故答案为:AB.
10.【答案】B,D
【解析】【解答】对于A, 当时,此时曲线为圆,A不符合题意,
对于B,若曲线为双曲线,则,即或, B对,
对于C, 若曲线为圆,则即,故曲线可能是圆,C不符合题意,
对于D, 曲线表示焦点在轴上的椭圆,则,解得,D对.
故答案为:BD
11.【答案】B,C,D
【解析】【解答】设椭圆的焦距为 ,由椭圆的定义可得 ,解得 , ,
由题意可得 ,解得 ,又 ,所以, ,
所以,该椭圆离心率的取值范围是 .
故符合条件的选项为BCD.
故答案为:BCD.
12.【答案】A,D
【解析】【解答】由双曲线方程知:渐近线方程为 ,而一条渐近线方程为 ,
∴ ,故 ,
∴双曲线:实轴长 ,离心率为 ,由于 可能在 不同分支上则有 ,焦距为 .
∴A、D符合题意,B、C不符合题意.
故答案为:AD
13.【答案】
【解析】【解答】当 时,整理抛物线方程得 ,即 ,
由抛物线 的焦点为 ,
所求焦点坐标为 .
当 时,同样可得.
故答案为: .
14.【答案】(25,0)
【解析】【解答】因为,所以,所以焦点的坐标为(25,0),
故答案为:(25,0).
15.【答案】
【解析】【解答】双曲线:,
,设是双曲线的左焦点,
圆的圆心为,半径为.
根据双曲线的定义有,
由于是圆的一点,为定点,
所以当共线时,最小,
即最小值为,
所以的最小值为.
故答案为:
16.【答案】
【解析】【解答】由题点 到圆 的距离等于点 到圆心 的距离减去半径.
当 时,显然不能满足点 到圆 的距离等于它到直线 的距离.故 ,此时 ,
两边平方有 .
故答案为:
17.【答案】(1)解:依题意,设椭圆的方程为 且 ),
因为椭圆过 两点,
所以
解得
因此,该椭圆的标准方程为 .
(2)设所求双曲线的方程为 ,
将点 代入双曲线方程得 ,
解得 ,
因此,所求双曲线的标准方程为 .
18.【答案】(1)解:由题意,设椭圆方程为 ,椭圆的半焦距为 ,
∴ ,解得 ,
∴ ;
(2)解:由余弦定理 ,
得 ,
∵点 是椭圆上的一个点,且 ,
∴ ,
∴ ,
∴ 的面积 .
19.【答案】解:⑴定义:平面内与一个定点F和一条定直线l(l不过F)的距离相等的点的集合叫做抛物线.这个定点F叫做抛物线的焦点,定直线l叫做抛物线的准线.
⑵过点F作直线l的垂线,垂足为K.以线段FK的中点O为坐标原点,
以直线FK为x轴建立平面直角坐标系,如图.
设 ,则焦点F的坐标为 ,
准线l的方程为 .
设 是抛物线上任意一点,点M到l的距离为d.
则 .即 ,
化简得: ,
所以,所求标准方程为 .
20.【答案】(1)解:由题意得 ,即 ,解得 ,又 ,可得 ,故双曲线C的标准方程为
(2)解:设角平分线与 轴交于点 ,根据角平分线性质可得 ,
, ,
设 ,联立方程 ,可得
,
即OP与OQ不垂直
21.【答案】(1)解:椭圆 过点 ,且焦点为 ,则 ,解得: ,所以椭圆方程为: .
(2)解:由 ,
故内切圆半径 ,
所以内切圆方程为:
22.【答案】(1)解:由题意: ,则 ,
设 ,则 , ,
二次函数开口向下,对称轴 ,在 上单调递减,
∴ 时函数值最大,此时 为椭圆的短轴的另一个端点,
∴椭圆是“圆椭圆”;
(2)解:由(1):椭圆方程: , ,
设 ,则 , , ,
∴二次项系数 ,函数开口向下,
由题意得,当且仅当 时函数值达到最大,
∴ ,解得: ,
综上, 的范围为 .
一、单选题
1.(·内江模拟)以椭圆 的短轴的一个端点和两焦点为顶点的三角形为等边三角形,且椭圆 上的点到左焦点的最大距离为6,则椭圆 的标准方程为( )
A. B. C. D.
2.(高二上·深圳期中)已知椭圆 的左,右焦点分别为 ,P是C上一点, 垂直于x轴, ,则C的方程为( )
A. B. C. D.
3.(高二上·安阳期中)已知方程表示焦点在轴上的椭圆,则实数的取值范围是()
A. B. C. D.
4.(高一下·镇江期末)已知椭圆 ( )过点 ,则实数a的值为( )
A.3 B.4 C.5 D.6
5.(·钦州模拟)圆 上一动点 ,抛物线 上一动点 ,则 的最小值为( )
A. B.2 C.3 D.4
6.(·南通模拟)双曲线 ( , )的左 右焦点分别为 , ,若 上存在点 满足 ,则该双曲线的离心率为( )
A. B. C. D.
7.(高二上·沧县期中)已知双曲线 的中心在原点,焦点在坐标轴上,则“双曲线 的离心率 ”是“双曲线 的渐近线方程为 ”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
8.(高二上·建瓯月考)已知 是双曲线 上一点,双曲线的一条渐近线方程为 , , 分别是双曲线的左、右焦点,若 ,则 ( )
A.7 B.6 C.5 D.3
二、多选题
9.(高三上·汕头月考)椭圆 的焦距为 ,则 的值为( )
A.9 B.23 C. D.
10.(高二上·浙江期中)若方程表示的曲线为,则下列说法正确的有( )
A.若曲线为椭圆,则
B.若曲线为双曲线,则或
C.曲线不可能是圆
D.若曲线表示焦点在轴上的椭圆,则
11.(高二下·扬州月考)在平面直角坐标系 中,椭圆 上存在点 ,使得 ,其中 、 分别为椭圆的左、右焦点,则该椭圆的离心率可能为( )
A. B. C. D.
12.(·潍坊模拟)已知双曲线 的左,右焦点分别为 ,一条渐近线方程为 , 为 上一点,则以下说法正确的是( )
A. 的实轴长为 B. 的离心率为
C. D. 的焦距为
三、填空题
13.(高二上·西安期中)抛物线的焦点坐标为 .
14.(高二上·毕节期末)抛物线的焦点坐标为 .
15.(·湖北模拟)已知双曲线:,F是双曲线C的右焦点,点A是双曲线C的左支上的一点,点B为圆D:上一点,则的最小值为 .
16.(高二下·上海期末)如果曲线C上的动点P到定点 的距离存在最小值,则称此最小值为点 到曲线C的距离.若点 到圆 的距离等于它到直线 的距离,则点 的轨迹方程是 .
四、解答题
17.(高二上·河南月考)
(1)求经过点 且焦点在坐标轴上的椭圆的标准方程﹔
(2)求与双曲线 有公共的渐近线,且过点 的双曲线的标准方程.
18.(高二上·莆田期中)已知椭圆两焦点 、 且经过点
(1)求椭圆的标准方程;
(2)若点 是椭圆上的一个点,且 ,求 的面积.
19.(高二上·绥德月考)叙述抛物线的定义,并推导抛物线的一个标准方程.
20.(·湛江模拟)已知双曲线C: =1(a,b>0)的左、右焦点分别为F1(-c,0),F2(c,0),其中c>0, M(c,3)在C上,且C的离心率为2.
(1)求C的标准方程;
(2)若O为坐标原点,∠F1MF2的角平分线l与曲线D: =1的交点为P,Q,试判断OP与OQ是否垂直,并说明理由.
21.(高二上·宁波期中)已知椭圆 焦点为 ,且过点 ,椭圆第一象限上的一点 到两焦点 的距离之差为2.
(1)求椭圆的标准方程;
(2)求 的内切圆方程.
22.(高二上·南京月考)已知椭圆 : ,点 为椭圆短轴的上端点, 为椭圆上异于 点的任一点,若 点到 点距离的最大值仅在 点为短轴的另一端点时取到,则称此椭圆为“圆椭圆”.
(1)若 ,判断椭圆 是否为“圆椭圆”;
(2)若椭圆 是“圆椭圆”,求 的取值范围.
答案解析部分
1.【答案】C
【解析】【解答】解:由题意知:短轴端点与焦点形成等边三角形,则 ,
椭圆上的点到左焦点最大距离为6,即 ,
则 , , .
则椭圆的标准方程为: .
故答案为:C.
2.【答案】C
【解析】【解答】解:因为 垂直于x轴, ,
所以 ,
所以 ,则 ,
所以C的方程为 .
故答案为:C.
3.【答案】D
【解析】【解答】由题知: 表示焦点在 轴上的椭圆,
所以
,
解得 。
故答案为:D.
4.【答案】B
【解析】【解答】解:因为椭圆过 ,所以 , ,所以 ,
故答案为:B.
5.【答案】B
【解析】【解答】如下图所示,过点 作抛物线 的准线 的垂线 ,垂足为点 ,
抛物线 的焦点为 ,圆 的圆心为 ,半径为1.
由抛物线的定义可得 ,则 ,
.
当且仅当 、 、 、 四点共线且点 、 在线段 上时, 取得最小值为2.
故答案为:B.
6.【答案】A
【解析】【解答】由 ,可知 ,又因为 为 的中点,
所以可得 .
根据题意设 ,则 ,
所以 ,
所以 ,
则 。
故答案为:A.
7.【答案】D
【解析】【解答】因为双曲线 的渐近线方程为 ,所以双曲线 的离心率 或
双曲线 的离心率 时, ,所以双曲线 的渐近线方程为 或 ,
因此“双曲线 的离心率 ”是“双曲线 的渐近线方程为 ”的既不充分也不必要条件
故答案为:D
8.【答案】A
【解析】【解答】解:由双曲线的方程、渐近线的方程可得 , .由双曲线的定义可得 ,
, (舍去)
故答案为:A .
9.【答案】A,B
【解析】【解答】解:椭圆 的焦距为 ,即 得 .
依题意当焦点在 轴上时,则 ,解得 ;
当焦点在 轴上时,则 ,解得 ,
∴ 的值为9或23.
故答案为:AB.
10.【答案】B,D
【解析】【解答】对于A, 当时,此时曲线为圆,A不符合题意,
对于B,若曲线为双曲线,则,即或, B对,
对于C, 若曲线为圆,则即,故曲线可能是圆,C不符合题意,
对于D, 曲线表示焦点在轴上的椭圆,则,解得,D对.
故答案为:BD
11.【答案】B,C,D
【解析】【解答】设椭圆的焦距为 ,由椭圆的定义可得 ,解得 , ,
由题意可得 ,解得 ,又 ,所以, ,
所以,该椭圆离心率的取值范围是 .
故符合条件的选项为BCD.
故答案为:BCD.
12.【答案】A,D
【解析】【解答】由双曲线方程知:渐近线方程为 ,而一条渐近线方程为 ,
∴ ,故 ,
∴双曲线:实轴长 ,离心率为 ,由于 可能在 不同分支上则有 ,焦距为 .
∴A、D符合题意,B、C不符合题意.
故答案为:AD
13.【答案】
【解析】【解答】当 时,整理抛物线方程得 ,即 ,
由抛物线 的焦点为 ,
所求焦点坐标为 .
当 时,同样可得.
故答案为: .
14.【答案】(25,0)
【解析】【解答】因为,所以,所以焦点的坐标为(25,0),
故答案为:(25,0).
15.【答案】
【解析】【解答】双曲线:,
,设是双曲线的左焦点,
圆的圆心为,半径为.
根据双曲线的定义有,
由于是圆的一点,为定点,
所以当共线时,最小,
即最小值为,
所以的最小值为.
故答案为:
16.【答案】
【解析】【解答】由题点 到圆 的距离等于点 到圆心 的距离减去半径.
当 时,显然不能满足点 到圆 的距离等于它到直线 的距离.故 ,此时 ,
两边平方有 .
故答案为:
17.【答案】(1)解:依题意,设椭圆的方程为 且 ),
因为椭圆过 两点,
所以
解得
因此,该椭圆的标准方程为 .
(2)设所求双曲线的方程为 ,
将点 代入双曲线方程得 ,
解得 ,
因此,所求双曲线的标准方程为 .
18.【答案】(1)解:由题意,设椭圆方程为 ,椭圆的半焦距为 ,
∴ ,解得 ,
∴ ;
(2)解:由余弦定理 ,
得 ,
∵点 是椭圆上的一个点,且 ,
∴ ,
∴ ,
∴ 的面积 .
19.【答案】解:⑴定义:平面内与一个定点F和一条定直线l(l不过F)的距离相等的点的集合叫做抛物线.这个定点F叫做抛物线的焦点,定直线l叫做抛物线的准线.
⑵过点F作直线l的垂线,垂足为K.以线段FK的中点O为坐标原点,
以直线FK为x轴建立平面直角坐标系,如图.
设 ,则焦点F的坐标为 ,
准线l的方程为 .
设 是抛物线上任意一点,点M到l的距离为d.
则 .即 ,
化简得: ,
所以,所求标准方程为 .
20.【答案】(1)解:由题意得 ,即 ,解得 ,又 ,可得 ,故双曲线C的标准方程为
(2)解:设角平分线与 轴交于点 ,根据角平分线性质可得 ,
, ,
设 ,联立方程 ,可得
,
即OP与OQ不垂直
21.【答案】(1)解:椭圆 过点 ,且焦点为 ,则 ,解得: ,所以椭圆方程为: .
(2)解:由 ,
故内切圆半径 ,
所以内切圆方程为:
22.【答案】(1)解:由题意: ,则 ,
设 ,则 , ,
二次函数开口向下,对称轴 ,在 上单调递减,
∴ 时函数值最大,此时 为椭圆的短轴的另一个端点,
∴椭圆是“圆椭圆”;
(2)解:由(1):椭圆方程: , ,
设 ,则 , , ,
∴二次项系数 ,函数开口向下,
由题意得,当且仅当 时函数值达到最大,
∴ ,解得: ,
综上, 的范围为 .
