6.3 球的表面积和体积 教学设计(表格式)
文档属性
| 名称 | 6.3 球的表面积和体积 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 877.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 16:15:14 | ||
图片预览


文档简介
教学设计
课 题 《球的表面积和体积》
课时安排 1 课前准备 制作课件、教具
教材内容 分 析 本节内容是北师大版(2019)高中数学第二册第六章第六节《球的表面积和体积》,它是在学生已经掌握了柱体、锥体、台体等基本几何体的表面积和体积的基础上,学习另一种基本几何体球体的体积和表面积,是本章的最后一节内容。球体是一种高度对称的基本空间几何体,也是进一步研究空间组合体结构特征的基础,本节内容为我们提供了一些求解空间几何体体积和表面积的思想方法。本节内容用1课时的时间完成。
设计理念 本节课体现了数据分析、直观想象、数学运算、逻辑推理的核心素养,因此本节课对体会单元核心思想方法具有举足轻重的地位和作用。在教学过程中坚持“厚基础、精实践、重应用”的教学方针,合理安排教学内容,贯彻“学生为主体、教师为主导”的教学理念,为学生创造循序渐进发现和解决问题的条件,通过小组合作探究,帮助学生深刻理解球的表面积和体积问题。具体体现在:在课堂教学中鼓励学生独立思考、敢于质疑,通过小组合作、交流分享,提升学生的合作探究意识,提高分析问题、解决问题的能力。强调一切以学生为中心,以提升学生认知水平、提高学生实践能力为目标,实现学生学习知识由被动接受向主动学习、主动探究和主动发现转变。
学情分析 学生具备一定的基本数学素养和观察分析、抽象概括及简单的归纳推理能力。同时,学生在日常生活中已有大量球体的认知,这都为本节课的学习奠定了良好的基础。在第二册中,通过前面对柱体、锥体、台体等几何体的表面积和体积问题的探究和学习,学生已经培养出了一定的空间想象能力,但因本节内容十分抽象,对学生空间想象能力的要求较高,故采用多媒体辅助教学,在希沃课件中,通过数学实验、用Geogebra制作多个几何动画,并录制成视频播放,尽可能形象直观的展示,帮助学生理解本节课的内容。
教学目标 1.知识目标 了解球的体积和表面积公式的推导过程,并掌握公式;了解本节课所用的思想方法;能运用球的体积和表面积公式灵活解决实际问题。 2.能力目标 通过数据分析、实验探究和推导球的体积和表面积公式的过程,培养学生的思维能力和空间想象能力;通过类比、观察、猜想等合情推理,提高学生分析、综合、抽象概括等逻辑推理能力;通过探究活动,让学生在观察、探究、发现中学习,在自主合作、交流中学习。 3.情感、态度与价值观 通过本节课内容学习,对球的体积和表面积公式的推导方法有了系统的了解,旨在提高学生数学思维能力和空间想象能力,增强学生探索和解决问题的信心。本节课教师以数学文化为情境,通过介绍中国古代割圆术和祖暅原理的巧妙,强调祖暅原理的提出比西方国家类似的结论早了一千多年,是中华民族的智慧和自豪,旨在增强学生的文化自信,为将来继承和发展古人智慧和中华民族生生不息的探索精神奠定基础。
教学重难点 1、教学重点:引导学生了解推导球的体积和面积公式所运用的基本思想方法。 2、教学难点:推导球的体积和面积公式中空间想象能力的形成。
教学过程
教学环节(一) 师生活动 1、新知探究 实验探究:将图1杯子倒满水,然后将这些水倒入图2杯子,并观察. 图1 半径为R的半球杯子 图2 底面半径和高都等于R的圆柱,中间挖去一个半径和高都等于R的圆锥杯子 师生活动:学生动手操作、思考,小组讨论,代表举手回答. 预设答案:这两个杯子容积相等
设计意图 培养学生探究及归纳能力.
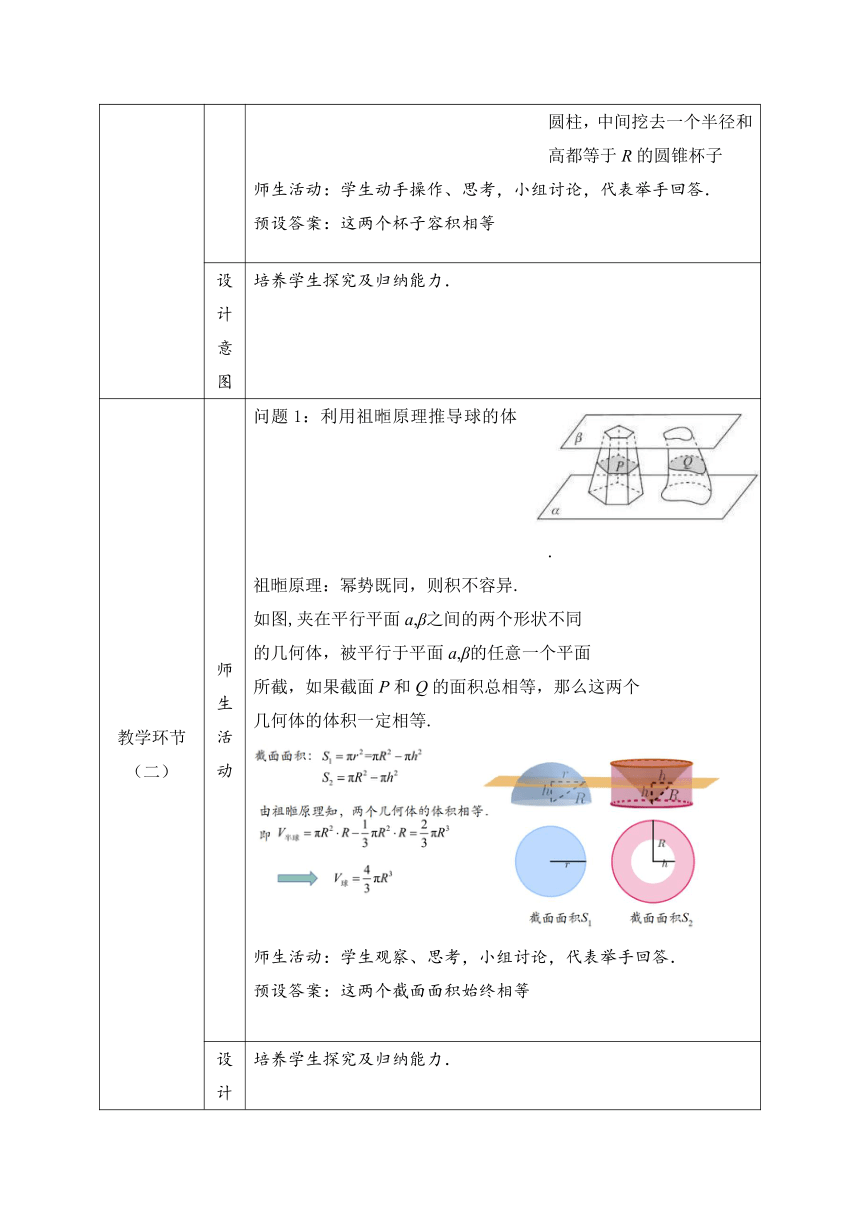
教学环节(二) 师生活动 问题1:利用祖暅原理推导球的体积公式. 祖暅原理:幂势既同,则积不容异. 如图,夹在平行平面a,β之间的两个形状不同 的几何体,被平行于平面a,β的任意一个平面 所截,如果截面P和Q的面积总相等,那么这两个 几何体的体积一定相等. 师生活动:学生观察、思考,小组讨论,代表举手回答. 预设答案:这两个截面面积始终相等
设计意图 培养学生探究及归纳能力.
教学环节 (三) 师生活动 问题2:如何在球的体积公式的基础上,推导球的表面积公式? 先回顾刘徽在为了解决圆周率的问题,提出的“割圆术”, 即将圆周用内接或外切正多边形穷竭的一种求圆面积和圆周长的方法. 师生活动:教师通过展示刘徽的“割圆术”,引导学生观察、思考,小组讨论,球能否类比此思想方法求表面积,代表举手回答. 预设答案:将球体进行切割,结合球的体积公式推导球的表面积公式.
设计意图 在学生已经了解刘徽割圆术的基础上,让学生初步感受到了“先分割,然后取近似,再求和,最后取极限”的思想方法,探究过程中仍然基于Geogebra软件及屏幕录制软件,制作了多个动态演示图,直观形象.让学生再次经历“提出问题——分析问题——解决问题”的形象探究过程,深刻感受球体表面积公式的形成过程.
教学环节 (四) 师生活动 2、应用举例 例1 如图,一个圆锥形的空杯子上面放着一个半球形的冰激凌,如果冰激凌融化了,会溢出杯子吗?(假设冰激凌融化前后体积不变) 例2 一个圆柱形的玻璃瓶的内半径为3cm,瓶里所装的水深为8cm,将一个钢球完全浸入水中,瓶中水的高度上升到8.5cm.求钢球的半径.
设计意图 让学生熟练掌握公式
教学环节 (五) 师生活动 4、归纳小结,布置作业 本节课我们学习了球的表面积、体积的计算公式,请你通过下列问题,归纳所学知识. (1)求球的体积与表面积的方法是什么? (2)解决有关球的问题时,常用哪些性质? 师生活动:学生尝试总结,老师适当补充. 预设答案: (1)求球的体积与表面积的方法:①要求球的体积或表面积,必须知道半径R或者通过条件能求出半径R,然后代入体积或表面积公式求解.②半径和球心是球的最关键要素,把握住了这两个要素,计算球的表面积或体积的相关题目也就易如反掌了. (2)解决有关球的问题时,常用以下性质:①用任意平面截球所得的截面是一个圆面,球心和截面圆圆心的连线与这个截面垂直.②如果分别用R和r表示球的半径和截面圆的半径,用d表示球心到截面的距离,则R2=r2+d2.球的有关计算问题,常归结为解直角三角形.
设计意图 复习巩固知识
板书设计 《球的表面积和体积》 1.体积 2.表面积 例题1 例题2 小结
教学反思 通过本节课通过实物操作结合学生已有经验推算球的体积公式,对其进行证明,整个过程一气呵成,逻辑严密,学生信服、印象深刻,同时体验到了学习的成就感。在今后的教学中应适当科普数学的重要作用,加入数学文化的内容,改变学生认为数学在生活中无用的固有思想。
课 题 《球的表面积和体积》
课时安排 1 课前准备 制作课件、教具
教材内容 分 析 本节内容是北师大版(2019)高中数学第二册第六章第六节《球的表面积和体积》,它是在学生已经掌握了柱体、锥体、台体等基本几何体的表面积和体积的基础上,学习另一种基本几何体球体的体积和表面积,是本章的最后一节内容。球体是一种高度对称的基本空间几何体,也是进一步研究空间组合体结构特征的基础,本节内容为我们提供了一些求解空间几何体体积和表面积的思想方法。本节内容用1课时的时间完成。
设计理念 本节课体现了数据分析、直观想象、数学运算、逻辑推理的核心素养,因此本节课对体会单元核心思想方法具有举足轻重的地位和作用。在教学过程中坚持“厚基础、精实践、重应用”的教学方针,合理安排教学内容,贯彻“学生为主体、教师为主导”的教学理念,为学生创造循序渐进发现和解决问题的条件,通过小组合作探究,帮助学生深刻理解球的表面积和体积问题。具体体现在:在课堂教学中鼓励学生独立思考、敢于质疑,通过小组合作、交流分享,提升学生的合作探究意识,提高分析问题、解决问题的能力。强调一切以学生为中心,以提升学生认知水平、提高学生实践能力为目标,实现学生学习知识由被动接受向主动学习、主动探究和主动发现转变。
学情分析 学生具备一定的基本数学素养和观察分析、抽象概括及简单的归纳推理能力。同时,学生在日常生活中已有大量球体的认知,这都为本节课的学习奠定了良好的基础。在第二册中,通过前面对柱体、锥体、台体等几何体的表面积和体积问题的探究和学习,学生已经培养出了一定的空间想象能力,但因本节内容十分抽象,对学生空间想象能力的要求较高,故采用多媒体辅助教学,在希沃课件中,通过数学实验、用Geogebra制作多个几何动画,并录制成视频播放,尽可能形象直观的展示,帮助学生理解本节课的内容。
教学目标 1.知识目标 了解球的体积和表面积公式的推导过程,并掌握公式;了解本节课所用的思想方法;能运用球的体积和表面积公式灵活解决实际问题。 2.能力目标 通过数据分析、实验探究和推导球的体积和表面积公式的过程,培养学生的思维能力和空间想象能力;通过类比、观察、猜想等合情推理,提高学生分析、综合、抽象概括等逻辑推理能力;通过探究活动,让学生在观察、探究、发现中学习,在自主合作、交流中学习。 3.情感、态度与价值观 通过本节课内容学习,对球的体积和表面积公式的推导方法有了系统的了解,旨在提高学生数学思维能力和空间想象能力,增强学生探索和解决问题的信心。本节课教师以数学文化为情境,通过介绍中国古代割圆术和祖暅原理的巧妙,强调祖暅原理的提出比西方国家类似的结论早了一千多年,是中华民族的智慧和自豪,旨在增强学生的文化自信,为将来继承和发展古人智慧和中华民族生生不息的探索精神奠定基础。
教学重难点 1、教学重点:引导学生了解推导球的体积和面积公式所运用的基本思想方法。 2、教学难点:推导球的体积和面积公式中空间想象能力的形成。
教学过程
教学环节(一) 师生活动 1、新知探究 实验探究:将图1杯子倒满水,然后将这些水倒入图2杯子,并观察. 图1 半径为R的半球杯子 图2 底面半径和高都等于R的圆柱,中间挖去一个半径和高都等于R的圆锥杯子 师生活动:学生动手操作、思考,小组讨论,代表举手回答. 预设答案:这两个杯子容积相等
设计意图 培养学生探究及归纳能力.
教学环节(二) 师生活动 问题1:利用祖暅原理推导球的体积公式. 祖暅原理:幂势既同,则积不容异. 如图,夹在平行平面a,β之间的两个形状不同 的几何体,被平行于平面a,β的任意一个平面 所截,如果截面P和Q的面积总相等,那么这两个 几何体的体积一定相等. 师生活动:学生观察、思考,小组讨论,代表举手回答. 预设答案:这两个截面面积始终相等
设计意图 培养学生探究及归纳能力.
教学环节 (三) 师生活动 问题2:如何在球的体积公式的基础上,推导球的表面积公式? 先回顾刘徽在为了解决圆周率的问题,提出的“割圆术”, 即将圆周用内接或外切正多边形穷竭的一种求圆面积和圆周长的方法. 师生活动:教师通过展示刘徽的“割圆术”,引导学生观察、思考,小组讨论,球能否类比此思想方法求表面积,代表举手回答. 预设答案:将球体进行切割,结合球的体积公式推导球的表面积公式.
设计意图 在学生已经了解刘徽割圆术的基础上,让学生初步感受到了“先分割,然后取近似,再求和,最后取极限”的思想方法,探究过程中仍然基于Geogebra软件及屏幕录制软件,制作了多个动态演示图,直观形象.让学生再次经历“提出问题——分析问题——解决问题”的形象探究过程,深刻感受球体表面积公式的形成过程.
教学环节 (四) 师生活动 2、应用举例 例1 如图,一个圆锥形的空杯子上面放着一个半球形的冰激凌,如果冰激凌融化了,会溢出杯子吗?(假设冰激凌融化前后体积不变) 例2 一个圆柱形的玻璃瓶的内半径为3cm,瓶里所装的水深为8cm,将一个钢球完全浸入水中,瓶中水的高度上升到8.5cm.求钢球的半径.
设计意图 让学生熟练掌握公式
教学环节 (五) 师生活动 4、归纳小结,布置作业 本节课我们学习了球的表面积、体积的计算公式,请你通过下列问题,归纳所学知识. (1)求球的体积与表面积的方法是什么? (2)解决有关球的问题时,常用哪些性质? 师生活动:学生尝试总结,老师适当补充. 预设答案: (1)求球的体积与表面积的方法:①要求球的体积或表面积,必须知道半径R或者通过条件能求出半径R,然后代入体积或表面积公式求解.②半径和球心是球的最关键要素,把握住了这两个要素,计算球的表面积或体积的相关题目也就易如反掌了. (2)解决有关球的问题时,常用以下性质:①用任意平面截球所得的截面是一个圆面,球心和截面圆圆心的连线与这个截面垂直.②如果分别用R和r表示球的半径和截面圆的半径,用d表示球心到截面的距离,则R2=r2+d2.球的有关计算问题,常归结为解直角三角形.
设计意图 复习巩固知识
板书设计 《球的表面积和体积》 1.体积 2.表面积 例题1 例题2 小结
教学反思 通过本节课通过实物操作结合学生已有经验推算球的体积公式,对其进行证明,整个过程一气呵成,逻辑严密,学生信服、印象深刻,同时体验到了学习的成就感。在今后的教学中应适当科普数学的重要作用,加入数学文化的内容,改变学生认为数学在生活中无用的固有思想。
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
