等差数列前n项和之有效教学设计
文档属性
| 名称 | 等差数列前n项和之有效教学设计 |

|
|
| 格式 | rar | ||
| 文件大小 | 937.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-02 00:00:00 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
新课程有效教学案例之18
教 学 案 例
学校名称:太谷二中
课程名称: 数 学
内容主题:等差数列的前n项和
教材版本:人教版
教师姓名: 黄海明
教 龄: 2
授课年级 高二年级 学科 数学 主题 等差数列的前n项和 任课教师 冯慧军
课型 问题拓展课 课时 1 授课日期 2009年8月28日
教材分析 1.本小节重点是等差数列的前n项和公式.学习中可能遇到的困难是获得推导公式的思路,克服困难的关键是通过具体例子发现一般规律. 2.本小节首先通过高斯算法,发现等差数列任意的第k项与倒数第n+1-k项的和等于首项、末项的和,从而得出求和的一般思路。
学生分析 本班的学生是在已具备了一些数列简单知识和具有较强分析能力的情况下,去进一步学习等差数列的前n项和的。这个班的学生,大多数对来源于实际生活的事例具有较高的兴趣,加上本班学生的思维较为活跃,大多喜欢交流,合作探究问题,导学中应多通过学生的经验和亲身感受来发展思维,应极力推行在“做”中学与在“作”中学,并通过体验式的实验来调动学生的学习欲望。对于个别学生较为内向的,应在分组时予以特别关注,促使其积极发言。
设计理念 1教师是学生学习的组织者、促进者、合作者: 在本节课的导学过程中,教师应以学生现在的认知水平和认知结构,选取适当的有利于完成教学目标的教学方法,有利于使学生积极投入到学习活动中,并根据初三学生的年龄特点,精心创设情景,方法要合理多样。2 学生是学习的主人: 在教师的指导下,通过学生主动的、富有个性的学习,学生用自己的亲身体验去感悟学习。在整个导学过程中,应保持学生的学习热情高涨,积极思考问题和参与问题的解决。激发学生的情感因素,调动积极性,做到课堂上人人参与,气氛和谐。
教学要求 1.鼓励学生多角度,多方法的分析解决问题,培养学生的发散性思维,避免思维的单一性。2.形成实事求是的态度,形成敢于质疑、善于思考以及乐于合作的学习习惯.3.千方百计的调动学生参与课堂的积极性,让学生成为课堂的主人。
教学目标 1、知识目标(1)掌握等差数列前n项和公式,理解公式的推导方法;(2)能较熟练应用等差数列前n项和公式求和。2、能力目标经历公式的推导过程,体会数形结合的数学思想,体验从特殊到一般的研究方法,学会观察、归纳、反思和逻辑推理的能力。3、情感目标通过生动具体的现实问题,激发学生探究的兴趣和欲望,树立学生求真的勇气和自信心,增强学生学好数学的心理体验,产生热爱数学的情感,体验在学习中获得成功。
重点、难点 本节教学重点是探索并掌握等差数列前n项和公式,学会用公式解决一些实际问题;难点是等差数列前n项和公式推导思路的获得.
关键问题 掌握等差数列前n项和公式,学会用公式解决一些实际问题;
教学方法 1、引导法:采用“问题情境——建立模型——解析、讲解--拓展与应用”的模式展开导学。2、情景教学法;充分联系生活,尽可能增加导学过程中的趣味性、实践性、利用媒体教学课件和实物模型等丰富学生的学习资源,让学生动手操作和自主参与。3、小组合作学习法:通过丰富多彩的集体讨论、小组活动,以合作学习促进自主探究。
教学准备 学教案的精心撰写,教学多媒体课件、投影仪。 教师课前结构化备课,制定本节课的导学单。
教 学 过 程 设 计
程序(要素) 时间 创设情景 教师行为 期望的学生行为
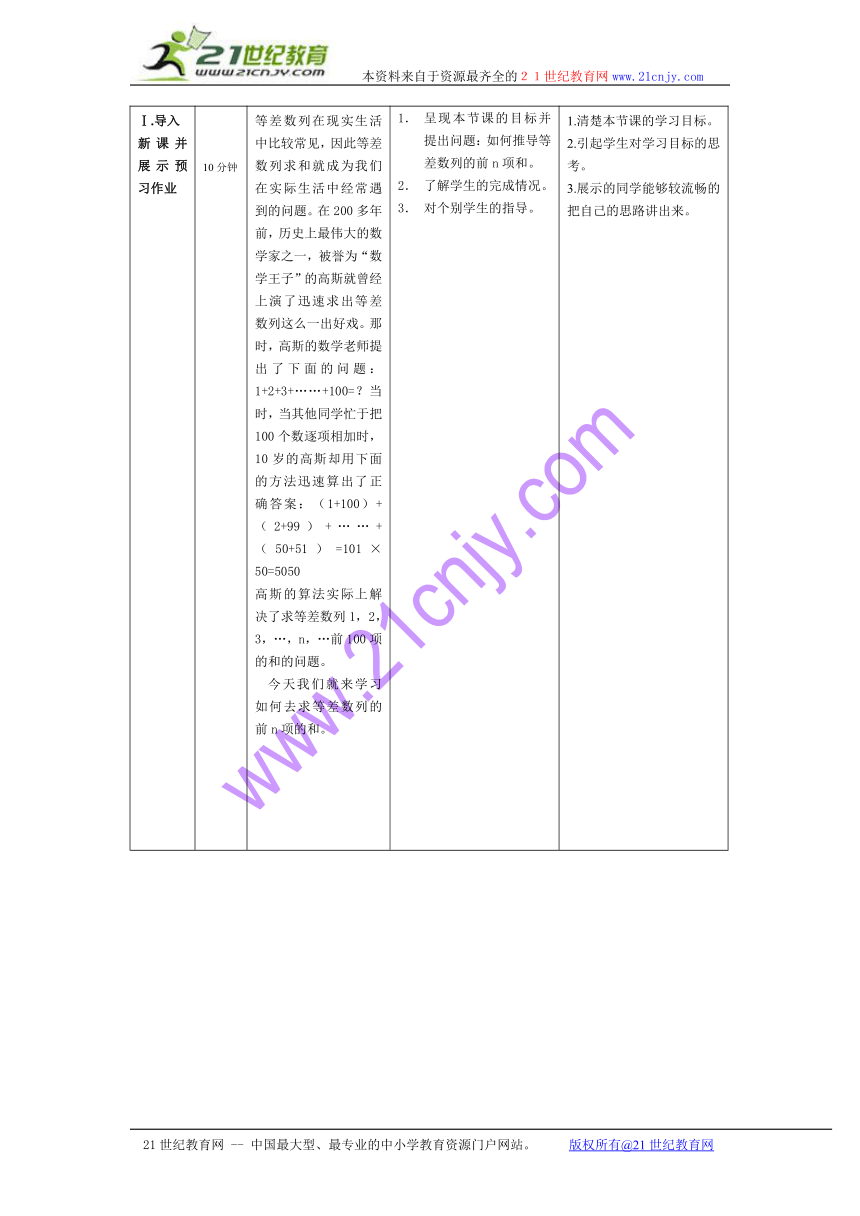
Ⅰ.导入新课并展示预习作业 10分钟 等差数列在现实生活中比较常见,因此等差数列求和就成为我们在实际生活中经常遇到的问题。在200多年前,历史上最伟大的数学家之一,被誉为“数学王子”的高斯就曾经上演了迅速求出等差数列这么一出好戏。那时,高斯的数学老师提出了下面的问题:1+2+3+……+100=?当时,当其他同学忙于把100个数逐项相加时,10岁的高斯却用下面的方法迅速算出了正确答案:(1+100)+(2+99)+……+(50+51)=101×50=5050高斯的算法实际上解决了求等差数列1,2,3,…,n,…前100项的和的问题。 今天我们就来学习如何去求等差数列的前n项的和。 呈现本节课的目标并提出问题:如何推导等差数列的前n项和。了解学生的完成情况。对个别学生的指导。 1.清楚本节课的学习目标。2.引起学生对学习目标的思考。3.展示的同学能够较流畅的把自己的思路讲出来。
Ⅱ尝试新课,并组内交流讨论 12分钟 创设拓展情境学生独立做十分钟,小组内交流两分钟。 1.借助几何图形的直观性,能启迪思路,唤醒学生记忆深处的东西,并为倒序相加法的出现提供了一个直接的模型.2.组织学生合作交流,探索展示。3.巡视学生学习活动情况。 希望从高斯的例子会推导等差数列的前n项和。大部分同学对例题能理解。对等差数列的前n项和的两个公式能灵活运用。
Ⅲ.班内展示 6分钟 学生板演,讲解 1.组织学生开展班内讨论。2.引导同学们总结:(1)倒序相加法(2)公式一(3)公式二 1.能够较流畅的把思路讲出来。2.听讲的同学能及时提出自己的疑问
Ⅳ.做问题训练单,组内对答案 9分钟 巩固训练 巡视,了解学生完成情况。对个别学生指导。 能够利用上面所学的知识方法解决问题。
Ⅴ。总结收获 3分钟 通过这节课的学习,你有哪些收获? 组织学生总结本节课的收获知识方法,以及学习的体验。 1 能够体验倒序相加法的妙处。2 能够正确运用等差数列的前n项和的两个公式。
课外拓展 数列{}的前n项和= + + + …+ ,求;
板书设计 3.3等差数列的前n项和 例1.分析:……………… 解:……………………… 猜 想 例2.分析:………………… 1. 解:……………………2.等差数列前n项和公式的推导过程 例3.分析:………………… …… 解:……………………………………………………………………………
教学反思 1、合理地对教材进行了个性化处理,挖掘了教材中可探究的因素,促使学生探究、推导。例如:等差数列前n项和的公式一,是通过具体的例子,引到一般的情况,激励学生进行猜想,再进行论证得出;而第二个公式并不象书本上那样直接给出,而是让学生从习题中进行归纳总结得到的。这样处理教材,使学生的思维得到了很大的锻炼。2、本节课教学过程的难点在于如何获得推导公式的“倒序相加法”这一思路.为了突破这一难点,在教学中采用了以问题驱动的教学方法,设计的三个问题体现了分析、解决问题的一般思路,即从特殊问题的解决中提炼方法,再试图运用这一方法解决一般问题.在教学过程中,通过教师的层层引导、学生的合作学习与自主探究,尤其是借助图形的直观性,学生“倒序相加法”思路的获得就水到渠成了.
简介:本节课教学内容是《普通高中课程标准实验教科书·数学(5)》(人教A版)中第二章的第三节“等差数列的前n项和”(第一课时).本节课主要研究如何应用倒序相加法求等差数列的前n项和以及该求和公式的应用.如何从首尾配对法引出倒序相加法,这是教学中必须注意的.
片
照片
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
新课程有效教学案例之18
教 学 案 例
学校名称:太谷二中
课程名称: 数 学
内容主题:等差数列的前n项和
教材版本:人教版
教师姓名: 黄海明
教 龄: 2
授课年级 高二年级 学科 数学 主题 等差数列的前n项和 任课教师 冯慧军
课型 问题拓展课 课时 1 授课日期 2009年8月28日
教材分析 1.本小节重点是等差数列的前n项和公式.学习中可能遇到的困难是获得推导公式的思路,克服困难的关键是通过具体例子发现一般规律. 2.本小节首先通过高斯算法,发现等差数列任意的第k项与倒数第n+1-k项的和等于首项、末项的和,从而得出求和的一般思路。
学生分析 本班的学生是在已具备了一些数列简单知识和具有较强分析能力的情况下,去进一步学习等差数列的前n项和的。这个班的学生,大多数对来源于实际生活的事例具有较高的兴趣,加上本班学生的思维较为活跃,大多喜欢交流,合作探究问题,导学中应多通过学生的经验和亲身感受来发展思维,应极力推行在“做”中学与在“作”中学,并通过体验式的实验来调动学生的学习欲望。对于个别学生较为内向的,应在分组时予以特别关注,促使其积极发言。
设计理念 1教师是学生学习的组织者、促进者、合作者: 在本节课的导学过程中,教师应以学生现在的认知水平和认知结构,选取适当的有利于完成教学目标的教学方法,有利于使学生积极投入到学习活动中,并根据初三学生的年龄特点,精心创设情景,方法要合理多样。2 学生是学习的主人: 在教师的指导下,通过学生主动的、富有个性的学习,学生用自己的亲身体验去感悟学习。在整个导学过程中,应保持学生的学习热情高涨,积极思考问题和参与问题的解决。激发学生的情感因素,调动积极性,做到课堂上人人参与,气氛和谐。
教学要求 1.鼓励学生多角度,多方法的分析解决问题,培养学生的发散性思维,避免思维的单一性。2.形成实事求是的态度,形成敢于质疑、善于思考以及乐于合作的学习习惯.3.千方百计的调动学生参与课堂的积极性,让学生成为课堂的主人。
教学目标 1、知识目标(1)掌握等差数列前n项和公式,理解公式的推导方法;(2)能较熟练应用等差数列前n项和公式求和。2、能力目标经历公式的推导过程,体会数形结合的数学思想,体验从特殊到一般的研究方法,学会观察、归纳、反思和逻辑推理的能力。3、情感目标通过生动具体的现实问题,激发学生探究的兴趣和欲望,树立学生求真的勇气和自信心,增强学生学好数学的心理体验,产生热爱数学的情感,体验在学习中获得成功。
重点、难点 本节教学重点是探索并掌握等差数列前n项和公式,学会用公式解决一些实际问题;难点是等差数列前n项和公式推导思路的获得.
关键问题 掌握等差数列前n项和公式,学会用公式解决一些实际问题;
教学方法 1、引导法:采用“问题情境——建立模型——解析、讲解--拓展与应用”的模式展开导学。2、情景教学法;充分联系生活,尽可能增加导学过程中的趣味性、实践性、利用媒体教学课件和实物模型等丰富学生的学习资源,让学生动手操作和自主参与。3、小组合作学习法:通过丰富多彩的集体讨论、小组活动,以合作学习促进自主探究。
教学准备 学教案的精心撰写,教学多媒体课件、投影仪。 教师课前结构化备课,制定本节课的导学单。
教 学 过 程 设 计
程序(要素) 时间 创设情景 教师行为 期望的学生行为
Ⅰ.导入新课并展示预习作业 10分钟 等差数列在现实生活中比较常见,因此等差数列求和就成为我们在实际生活中经常遇到的问题。在200多年前,历史上最伟大的数学家之一,被誉为“数学王子”的高斯就曾经上演了迅速求出等差数列这么一出好戏。那时,高斯的数学老师提出了下面的问题:1+2+3+……+100=?当时,当其他同学忙于把100个数逐项相加时,10岁的高斯却用下面的方法迅速算出了正确答案:(1+100)+(2+99)+……+(50+51)=101×50=5050高斯的算法实际上解决了求等差数列1,2,3,…,n,…前100项的和的问题。 今天我们就来学习如何去求等差数列的前n项的和。 呈现本节课的目标并提出问题:如何推导等差数列的前n项和。了解学生的完成情况。对个别学生的指导。 1.清楚本节课的学习目标。2.引起学生对学习目标的思考。3.展示的同学能够较流畅的把自己的思路讲出来。
Ⅱ尝试新课,并组内交流讨论 12分钟 创设拓展情境学生独立做十分钟,小组内交流两分钟。 1.借助几何图形的直观性,能启迪思路,唤醒学生记忆深处的东西,并为倒序相加法的出现提供了一个直接的模型.2.组织学生合作交流,探索展示。3.巡视学生学习活动情况。 希望从高斯的例子会推导等差数列的前n项和。大部分同学对例题能理解。对等差数列的前n项和的两个公式能灵活运用。
Ⅲ.班内展示 6分钟 学生板演,讲解 1.组织学生开展班内讨论。2.引导同学们总结:(1)倒序相加法(2)公式一(3)公式二 1.能够较流畅的把思路讲出来。2.听讲的同学能及时提出自己的疑问
Ⅳ.做问题训练单,组内对答案 9分钟 巩固训练 巡视,了解学生完成情况。对个别学生指导。 能够利用上面所学的知识方法解决问题。
Ⅴ。总结收获 3分钟 通过这节课的学习,你有哪些收获? 组织学生总结本节课的收获知识方法,以及学习的体验。 1 能够体验倒序相加法的妙处。2 能够正确运用等差数列的前n项和的两个公式。
课外拓展 数列{}的前n项和= + + + …+ ,求;
板书设计 3.3等差数列的前n项和 例1.分析:……………… 解:……………………… 猜 想 例2.分析:………………… 1. 解:……………………2.等差数列前n项和公式的推导过程 例3.分析:………………… …… 解:……………………………………………………………………………
教学反思 1、合理地对教材进行了个性化处理,挖掘了教材中可探究的因素,促使学生探究、推导。例如:等差数列前n项和的公式一,是通过具体的例子,引到一般的情况,激励学生进行猜想,再进行论证得出;而第二个公式并不象书本上那样直接给出,而是让学生从习题中进行归纳总结得到的。这样处理教材,使学生的思维得到了很大的锻炼。2、本节课教学过程的难点在于如何获得推导公式的“倒序相加法”这一思路.为了突破这一难点,在教学中采用了以问题驱动的教学方法,设计的三个问题体现了分析、解决问题的一般思路,即从特殊问题的解决中提炼方法,再试图运用这一方法解决一般问题.在教学过程中,通过教师的层层引导、学生的合作学习与自主探究,尤其是借助图形的直观性,学生“倒序相加法”思路的获得就水到渠成了.
简介:本节课教学内容是《普通高中课程标准实验教科书·数学(5)》(人教A版)中第二章的第三节“等差数列的前n项和”(第一课时).本节课主要研究如何应用倒序相加法求等差数列的前n项和以及该求和公式的应用.如何从首尾配对法引出倒序相加法,这是教学中必须注意的.
片
照片
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
