异面直线的概念和判定
图片预览



文档简介
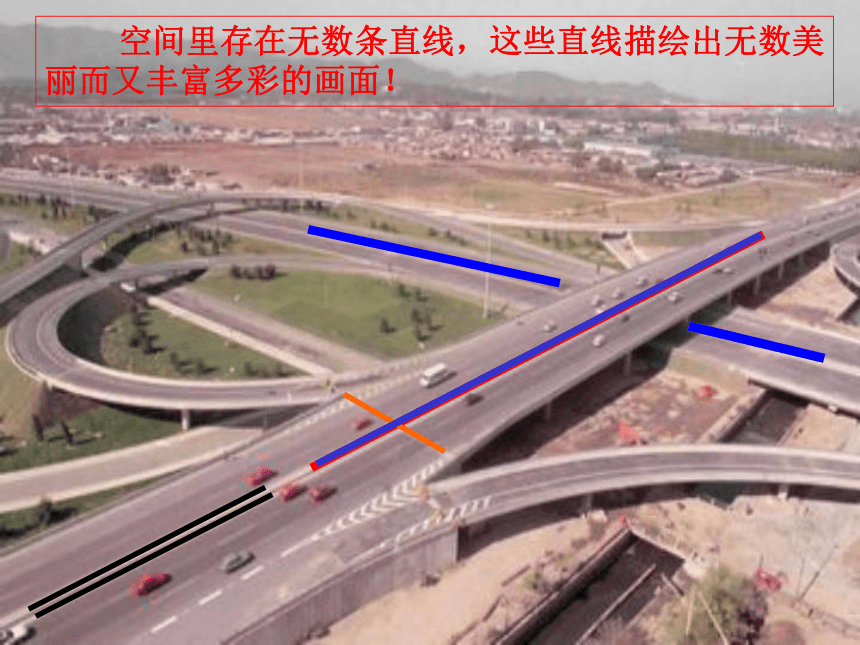
课件16张PPT。高中数学必修二1.2.2 空间两条直线的位置关系(2)异面直线 空间里存在无数条直线,这些直线描绘出无数美
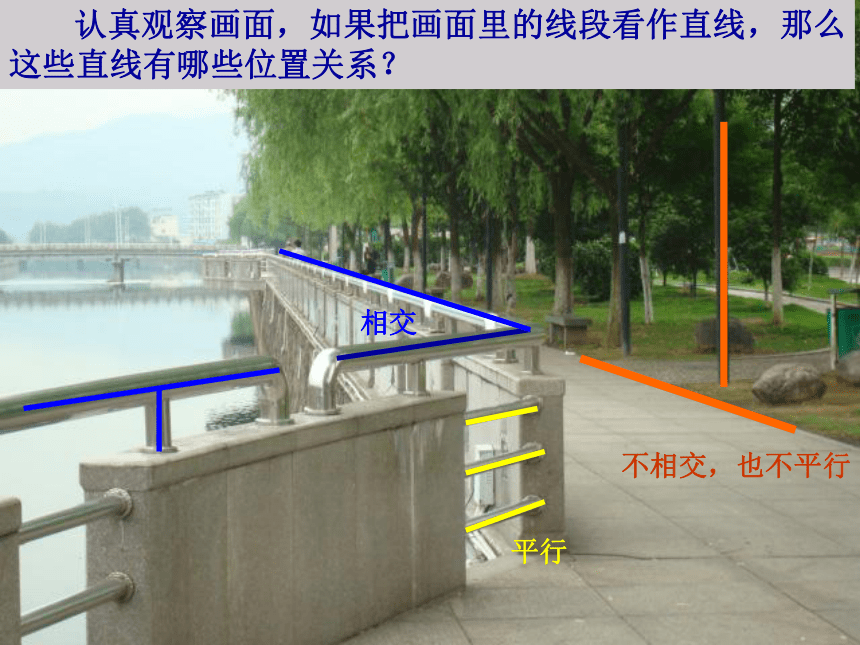
丽而又丰富多彩的画面! 认真观察画面,如果把画面里的线段看作直线,那么
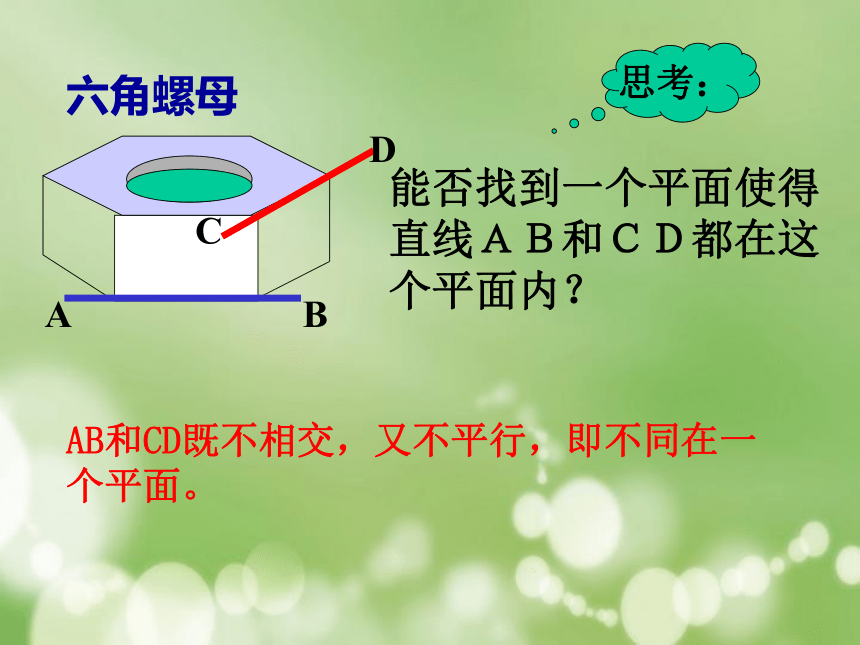
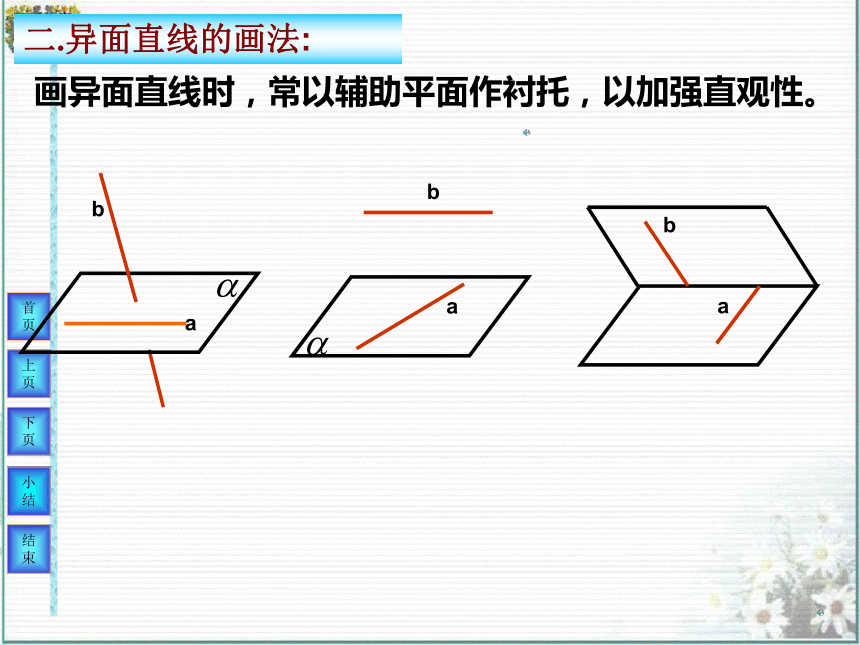
这些直线有哪些位置关系?相交平行不相交,也不平行六角螺母能否找到一个平面使得直线AB和CD都在这个平面内?思考:AB和CD既不相交,又不平行,即不同在一个平面。一.异面直线的定义:空间两条直线的位置关系相交平行异面记为:a∩b=A.记为a∥b.画异面直线时,常以辅助平面作衬托,以加强直观性。ababab二.异面直线的画法:(2)分别在两个平面内的直线叫异面直线.练习1、判断:(1)没有公共点的两直线叫异面直线. 2、说出正方体中哪些棱与下列线段所在直线是异面直线关系?1) A1C;AA1;
3)CB1; 3、下列图形中,能确定直线a、b是异面直线的是( )分析:用定义证明(反证法步骤:反设,归谬,结论)证明:假设直线AB和l 不是异面直线, 那么A∈α,这与已知点A在平面 外矛盾,假设不成立. 所以直线AB和l 是异面直线.则直线AB和l 共面,设这个平面为 ,例1.求证过平面外一点和平面内一点的直线,与平
面内不经过该点的直线是异面直线.三、异面直线的判定定理
连接平面内一点与平面外一点的直线,和平面内不
经过此点的直线是异面直线. 例2:已知空间四边形ABCD,E、F分别为BC、DA的中点.
求证:AE和CF是异面直线。ABCEF证明1:(反证法)
假设AE和CF在同一个平面α内,
则有 A∈α、E∈α、C∈α、F∈α因为B∈CE,D∈AF所以B∈α、D∈α所以A、B、C、D共面所以AE和CF是异面直线这与已知四边形ABCD为空间四边形矛盾DABCDEF所以AE和CF是异面直线证明2(定理法):练习:1、已知不共面的三直线a,b,c相交于点O,M,P是a上两点,N,Q分别在b,c上 .
求证:MN,PQ异面.162、选择题:(1)一条直线和两条异面直线中的一条平行,
则它和另一条的位置关系是 ( )
A 平行 B 相交 C 异面 D 相交或异面DA(2)和两条异面直线AB,CD都相交的两条直线 AC,BD 的位置关系是 ( )
A 一定是异面直线 B 一定是相交直线
C 可能是平行直线 D 可能异面,也可能是相交(3)下列命题假命题的是( )①两条直线都和同一个平面平行,则这两条直线平行。
②两条直线都没有公共点,则这两条直线平行。
③两条直线都和第三条直线垂直,则这两条直线 平行。
④一条直线和两条平行直线都相交,那么这三条直线共面①②③四. 小 结1.异面直线的概念;
2. 空间中两条异面直线的画法;
3.异面直线的判定和证明;
①定义法(常用反证法);
②定理法。感谢光临指导作业 :1. P31 习题1.2: 12 、13 、14
2.预习p29 异面直线的夹角。
丽而又丰富多彩的画面! 认真观察画面,如果把画面里的线段看作直线,那么
这些直线有哪些位置关系?相交平行不相交,也不平行六角螺母能否找到一个平面使得直线AB和CD都在这个平面内?思考:AB和CD既不相交,又不平行,即不同在一个平面。一.异面直线的定义:空间两条直线的位置关系相交平行异面记为:a∩b=A.记为a∥b.画异面直线时,常以辅助平面作衬托,以加强直观性。ababab二.异面直线的画法:(2)分别在两个平面内的直线叫异面直线.练习1、判断:(1)没有公共点的两直线叫异面直线. 2、说出正方体中哪些棱与下列线段所在直线是异面直线关系?1) A1C;AA1;
3)CB1; 3、下列图形中,能确定直线a、b是异面直线的是( )分析:用定义证明(反证法步骤:反设,归谬,结论)证明:假设直线AB和l 不是异面直线, 那么A∈α,这与已知点A在平面 外矛盾,假设不成立. 所以直线AB和l 是异面直线.则直线AB和l 共面,设这个平面为 ,例1.求证过平面外一点和平面内一点的直线,与平
面内不经过该点的直线是异面直线.三、异面直线的判定定理
连接平面内一点与平面外一点的直线,和平面内不
经过此点的直线是异面直线. 例2:已知空间四边形ABCD,E、F分别为BC、DA的中点.
求证:AE和CF是异面直线。ABCEF证明1:(反证法)
假设AE和CF在同一个平面α内,
则有 A∈α、E∈α、C∈α、F∈α因为B∈CE,D∈AF所以B∈α、D∈α所以A、B、C、D共面所以AE和CF是异面直线这与已知四边形ABCD为空间四边形矛盾DABCDEF所以AE和CF是异面直线证明2(定理法):练习:1、已知不共面的三直线a,b,c相交于点O,M,P是a上两点,N,Q分别在b,c上 .
求证:MN,PQ异面.162、选择题:(1)一条直线和两条异面直线中的一条平行,
则它和另一条的位置关系是 ( )
A 平行 B 相交 C 异面 D 相交或异面DA(2)和两条异面直线AB,CD都相交的两条直线 AC,BD 的位置关系是 ( )
A 一定是异面直线 B 一定是相交直线
C 可能是平行直线 D 可能异面,也可能是相交(3)下列命题假命题的是( )①两条直线都和同一个平面平行,则这两条直线平行。
②两条直线都没有公共点,则这两条直线平行。
③两条直线都和第三条直线垂直,则这两条直线 平行。
④一条直线和两条平行直线都相交,那么这三条直线共面①②③四. 小 结1.异面直线的概念;
2. 空间中两条异面直线的画法;
3.异面直线的判定和证明;
①定义法(常用反证法);
②定理法。感谢光临指导作业 :1. P31 习题1.2: 12 、13 、14
2.预习p29 异面直线的夹角。
