上海市黄浦区2010届高三暑假质量检测(数学文)(一)
文档属性
| 名称 | 上海市黄浦区2010届高三暑假质量检测(数学文)(一) |

|
|
| 格式 | rar | ||
| 文件大小 | 132.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-02 00:00:00 | ||
图片预览



文档简介
黄浦区2009-2010学年度高三年级暑假质量检测(一)
数学试卷(文科)
(2009年7月)
考生注意:
1、每位考生应同时收到试卷和答题纸两份材料,解答必须在答题纸上进行,写在试卷上的解答一律无效;
2、答卷前,考生务必将姓名、准考证号等相关信息在答题纸上填写清楚;
3、本试卷共21道试题,满分150分;考试时间120分钟.
一、填空题(本大题共12小题,每小题5分,共60分.只需将结果填写在答题纸上)
1、关于 .
2、函数的定义域是 .
3、若函数是定义域为R的偶函数,则实数 .
4、计算:= .
5、已知全集,,则
= .
6、某中学即将举行2009届高三学生毕业典礼,校领导准备从高三(1)班的7名优秀毕业生(3名男生,4名女生)中随机抽取2名学生在毕业典礼上发言,则抽到的2名学生恰好是1男1女的概率是 .
7、已知角的顶点在原点,始边与x轴正半轴重合,点P()是角终边上一点,则 .
8、把圆柱体的侧面沿母线展开后得到一个矩形,若矩形的一组邻边长分别为,则该圆柱体的体积是 .
9、直线经过点P相切,则直线的方程
是 .
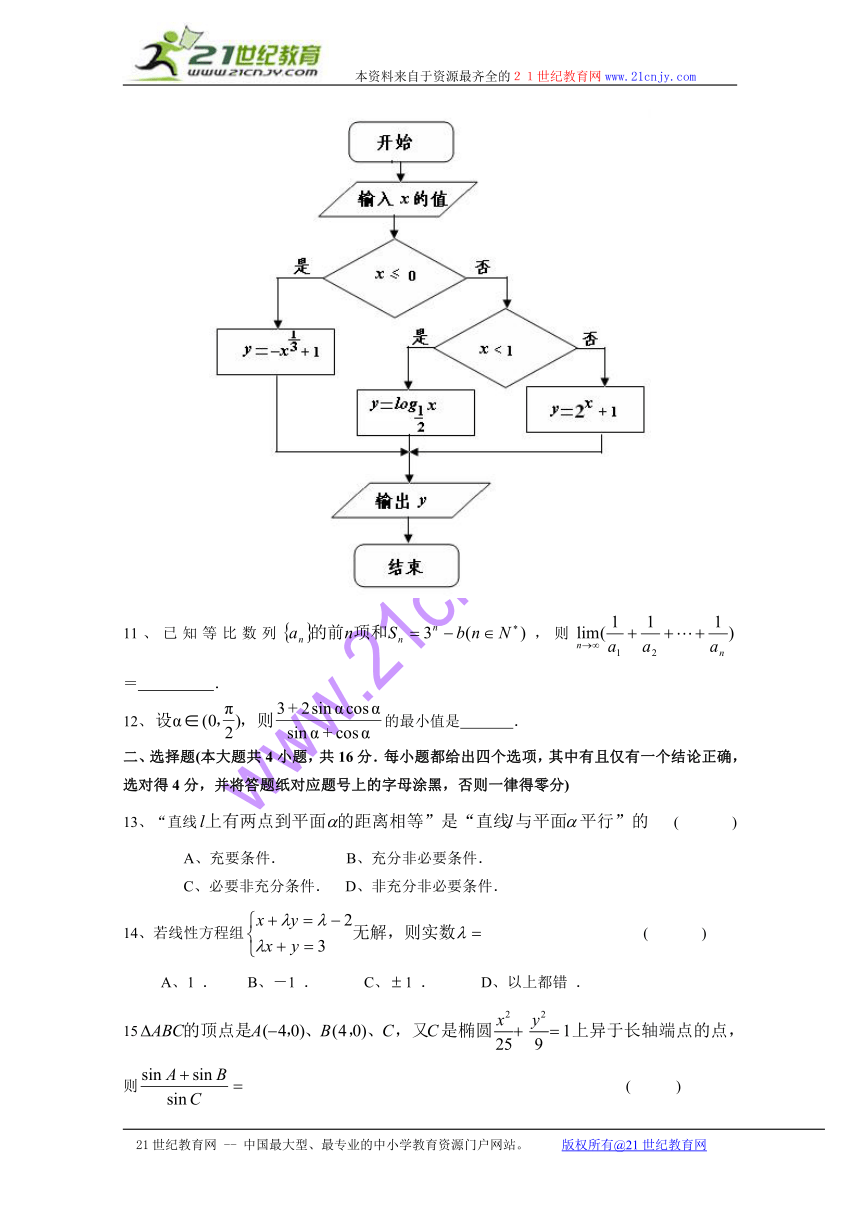
10、已知下列程序框图输出的结果是,则输入框中的所有可能值是 .
11、已知等比数列,则= .
12、的最小值是 .
二、选择题(本大题共4小题,共16分.每小题都给出四个选项,其中有且仅有一个结论正确,选对得4分,并将答题纸对应题号上的字母涂黑,否则一律得零分)
13、“直线 ( )
A、充要条件. B、充分非必要条件.
C、必要非充分条件. D、非充分非必要条件.
14、若线性方程组 ( )
A、1 . B、-1 . C、1 . D、以上都错 .
15
则 ( )
A、2. B、 . C、. D、 .
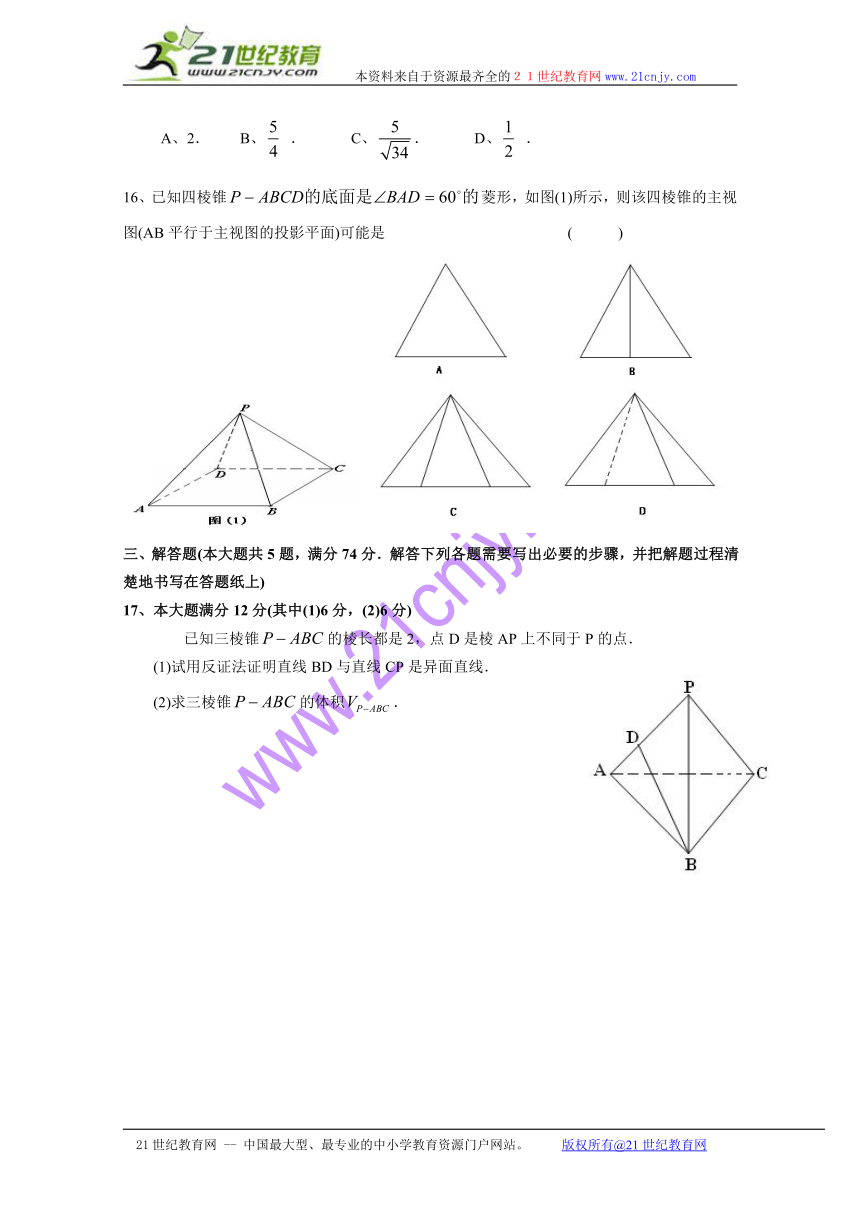
16、已知四棱锥菱形,如图(1)所示,则该四棱锥的主视图(AB平行于主视图的投影平面)可能是 ( )
三、解答题(本大题共5题,满分74分.解答下列各题需要写出必要的步骤,并把解题过程清楚地书写在答题纸上)
17、本大题满分12分(其中(1)6分,(2)6分)
已知三棱锥的棱长都是2,点D是棱AP上不同于P的点.
(1)试用反证法证明直线BD与直线CP是异面直线.
(2)求三棱锥的体积.
18、本大题满分12分
某工厂生产甲、乙两种产品所需原材料吨数及一周内可用工时总量如下表所示.
每吨甲产品消耗
每吨乙产品消耗
每周可供使用的总量
原材料(吨数)
3
2
16
生产时间(小时)
5
1
15
已知销售甲、乙产品每吨的利润分别为5万元和2万元.试问生产甲、乙两种产品各多少吨时,该厂每周获得的利润最大?
19、本大题满分16分(其中(1)8分,(2)8分)
已知,函数
.
(1)求的值.
(2)求函数.
20、本大题满分16分(其中(1)8分,(2)8分)
若数列
都成立,则我们把数列称为“L型数列”.
(1)试问等差是否为L型数列?若是,写出对应p、q的值;若不是,说明理由.
(2)已知L型数列满足,证明:数列是等比数列,并进一步求出的通项公式.
21、本大题满分18分(其中(1)8分,(2)10分)
已知点P满足,动点满足.
(1)求动点N所在曲线C的方程.
(2)若曲线C上的两点A、B满足(O为坐标原点,A、B不同于O点),试证明直线AB必过定点,并求出这个定点的坐标.
黄浦区2009年高考模拟考
数学试卷(文科)
参考答案和评分标准
说明:
1、本解答仅列出试题的一种解法,如果考生的解法与所列解答不同,可参考解答中的评分精神进行评分。
2、评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅,当考生的解答在某一步出现错误,影响了后继部分,但该步以后的解答未改变这一题的内容和难度时,可视影响程度决定后面部分的给分,这时原则上不应超过后面部分应给分数之半,如果有较严重的概念性错误,就不给分。
一、填空题:
1、 7、
2、 8、(只填一个给2分)
3、 9、
4、 1 10、
5、 11、
6、 12、
二、选择题: 13、C 14、A 15、B 16、D
三、解答题
17、本大题满分12分(其中(1)6分,(2)6分)
证明 (1)(反证法)假设BD与CP不是异面直线. 2分
设BD与CP都在平面上.,.又,.∴点A、B、C、P都在平面上,这与P、A、B、C不共面(P-ABC是三棱锥)矛盾,于是,假设不成立. 5分
所以直线BD与CP是异面直线. 6分
解(2) 设锥顶点P在底面的射影为O.∵P-ABC的棱长都是2,∴△ABC是正三角形.
∴,即O为底面三角形的中心,因此P-ABC为正三棱锥.联结BO并延长交AC于E,.
∵AB=BC=AC=PB=2,. 8分
,进一步可得. 10分
∴
=
= . 12分
18、本大题满分12分
解 设工厂一周内生产甲产品x吨、乙产品y吨,每周所获利润为z万元. 1分
依据题意,得约束条件为
. 4分
求目标函数的最大值. 6分
画出约束条件的可行域,如图阴影部分所示。 8分
将直线向上平移,可以发现,经过可行域的最后一个点B(2,5)时,函数的值最大(也可通过代凸多边形端点进行计算求得),最大值为5×2+2×5=20(万元). 11分
所以每周生产甲产品2吨,乙产品5吨时,工厂可获得的周利润最大(20万元).
12 分
19、本题满分16分(其中(1)8分,(2)8分)
解 (1)依据题意,有
=
= 3分
=
=. 6分
又,∴. 8分
(2) 由(1)可知,.
当. 10分
考察正弦函数的图像,进一步有,. 15分
所以函数. 16分
20、(本题满分16分,其中(1)8分,(2)8分)
(1) 答 等差数列都是L型数列.
理由 当数列, 1分
即,且相应的. 3分
所以等差数列是L型数列. 4分
同样,当数列, 5分
即,且相应的. 7分
所以等比数列是L型数列. 8分
证明 (2)∵,
∴
=. 10分
又,
∴数列. 12分
于是,,即().
∴因此,的等差数列.
14分
∴,
所以. 16分
21、本大题满分18分(其中(1)8分,(2)10分)
解 (1)设动点. 1分
依据题意,有,.3分
又,则
,进一步有.因此,. 7分
所以曲线C的方程是. 8分
证明(2) 因A、B是曲线C:上不同于原点的两点,
可设、,
则
、,. 11分
又,故.所以. 14分
由直线AB的法向量为,可得直线AB的方程:
,进一步化简为.16分
所以直线AB:恒过定点,且定点坐标为(4,0). 18分
证毕!
数学试卷(文科)
(2009年7月)
考生注意:
1、每位考生应同时收到试卷和答题纸两份材料,解答必须在答题纸上进行,写在试卷上的解答一律无效;
2、答卷前,考生务必将姓名、准考证号等相关信息在答题纸上填写清楚;
3、本试卷共21道试题,满分150分;考试时间120分钟.
一、填空题(本大题共12小题,每小题5分,共60分.只需将结果填写在答题纸上)
1、关于 .
2、函数的定义域是 .
3、若函数是定义域为R的偶函数,则实数 .
4、计算:= .
5、已知全集,,则
= .
6、某中学即将举行2009届高三学生毕业典礼,校领导准备从高三(1)班的7名优秀毕业生(3名男生,4名女生)中随机抽取2名学生在毕业典礼上发言,则抽到的2名学生恰好是1男1女的概率是 .
7、已知角的顶点在原点,始边与x轴正半轴重合,点P()是角终边上一点,则 .
8、把圆柱体的侧面沿母线展开后得到一个矩形,若矩形的一组邻边长分别为,则该圆柱体的体积是 .
9、直线经过点P相切,则直线的方程
是 .
10、已知下列程序框图输出的结果是,则输入框中的所有可能值是 .
11、已知等比数列,则= .
12、的最小值是 .
二、选择题(本大题共4小题,共16分.每小题都给出四个选项,其中有且仅有一个结论正确,选对得4分,并将答题纸对应题号上的字母涂黑,否则一律得零分)
13、“直线 ( )
A、充要条件. B、充分非必要条件.
C、必要非充分条件. D、非充分非必要条件.
14、若线性方程组 ( )
A、1 . B、-1 . C、1 . D、以上都错 .
15
则 ( )
A、2. B、 . C、. D、 .
16、已知四棱锥菱形,如图(1)所示,则该四棱锥的主视图(AB平行于主视图的投影平面)可能是 ( )
三、解答题(本大题共5题,满分74分.解答下列各题需要写出必要的步骤,并把解题过程清楚地书写在答题纸上)
17、本大题满分12分(其中(1)6分,(2)6分)
已知三棱锥的棱长都是2,点D是棱AP上不同于P的点.
(1)试用反证法证明直线BD与直线CP是异面直线.
(2)求三棱锥的体积.
18、本大题满分12分
某工厂生产甲、乙两种产品所需原材料吨数及一周内可用工时总量如下表所示.
每吨甲产品消耗
每吨乙产品消耗
每周可供使用的总量
原材料(吨数)
3
2
16
生产时间(小时)
5
1
15
已知销售甲、乙产品每吨的利润分别为5万元和2万元.试问生产甲、乙两种产品各多少吨时,该厂每周获得的利润最大?
19、本大题满分16分(其中(1)8分,(2)8分)
已知,函数
.
(1)求的值.
(2)求函数.
20、本大题满分16分(其中(1)8分,(2)8分)
若数列
都成立,则我们把数列称为“L型数列”.
(1)试问等差是否为L型数列?若是,写出对应p、q的值;若不是,说明理由.
(2)已知L型数列满足,证明:数列是等比数列,并进一步求出的通项公式.
21、本大题满分18分(其中(1)8分,(2)10分)
已知点P满足,动点满足.
(1)求动点N所在曲线C的方程.
(2)若曲线C上的两点A、B满足(O为坐标原点,A、B不同于O点),试证明直线AB必过定点,并求出这个定点的坐标.
黄浦区2009年高考模拟考
数学试卷(文科)
参考答案和评分标准
说明:
1、本解答仅列出试题的一种解法,如果考生的解法与所列解答不同,可参考解答中的评分精神进行评分。
2、评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅,当考生的解答在某一步出现错误,影响了后继部分,但该步以后的解答未改变这一题的内容和难度时,可视影响程度决定后面部分的给分,这时原则上不应超过后面部分应给分数之半,如果有较严重的概念性错误,就不给分。
一、填空题:
1、 7、
2、 8、(只填一个给2分)
3、 9、
4、 1 10、
5、 11、
6、 12、
二、选择题: 13、C 14、A 15、B 16、D
三、解答题
17、本大题满分12分(其中(1)6分,(2)6分)
证明 (1)(反证法)假设BD与CP不是异面直线. 2分
设BD与CP都在平面上.,.又,.∴点A、B、C、P都在平面上,这与P、A、B、C不共面(P-ABC是三棱锥)矛盾,于是,假设不成立. 5分
所以直线BD与CP是异面直线. 6分
解(2) 设锥顶点P在底面的射影为O.∵P-ABC的棱长都是2,∴△ABC是正三角形.
∴,即O为底面三角形的中心,因此P-ABC为正三棱锥.联结BO并延长交AC于E,.
∵AB=BC=AC=PB=2,. 8分
,进一步可得. 10分
∴
=
= . 12分
18、本大题满分12分
解 设工厂一周内生产甲产品x吨、乙产品y吨,每周所获利润为z万元. 1分
依据题意,得约束条件为
. 4分
求目标函数的最大值. 6分
画出约束条件的可行域,如图阴影部分所示。 8分
将直线向上平移,可以发现,经过可行域的最后一个点B(2,5)时,函数的值最大(也可通过代凸多边形端点进行计算求得),最大值为5×2+2×5=20(万元). 11分
所以每周生产甲产品2吨,乙产品5吨时,工厂可获得的周利润最大(20万元).
12 分
19、本题满分16分(其中(1)8分,(2)8分)
解 (1)依据题意,有
=
= 3分
=
=. 6分
又,∴. 8分
(2) 由(1)可知,.
当. 10分
考察正弦函数的图像,进一步有,. 15分
所以函数. 16分
20、(本题满分16分,其中(1)8分,(2)8分)
(1) 答 等差数列都是L型数列.
理由 当数列, 1分
即,且相应的. 3分
所以等差数列是L型数列. 4分
同样,当数列, 5分
即,且相应的. 7分
所以等比数列是L型数列. 8分
证明 (2)∵,
∴
=. 10分
又,
∴数列. 12分
于是,,即().
∴因此,的等差数列.
14分
∴,
所以. 16分
21、本大题满分18分(其中(1)8分,(2)10分)
解 (1)设动点. 1分
依据题意,有,.3分
又,则
,进一步有.因此,. 7分
所以曲线C的方程是. 8分
证明(2) 因A、B是曲线C:上不同于原点的两点,
可设、,
则
、,. 11分
又,故.所以. 14分
由直线AB的法向量为,可得直线AB的方程:
,进一步化简为.16分
所以直线AB:恒过定点,且定点坐标为(4,0). 18分
证毕!
同课章节目录
